基于PID和LQR算法的倒立擺控制設計

程明賀，陳倉

（長安大學，陜西 西安 710064）

專題 汽車設計與研究

基于PID和LQR算法的倒立擺控制設計

程明賀，陳倉

（長安大學，陜西 西安 710064）

文章建立了一級倒立擺的數學模型，并在此基礎上通過MATLAB仿真工具對一級倒立擺的PID（Proportion Integration Differentiation）及LQR（Linear Quadratic Regulator）控制算法進行了設計與仿真。一般而言LQR控制算法的控制性能要優于PID控制算法。

倒立擺；PID；LQR

10.16638/j.cnki.1671-7988.2017.05.001

CLC NO.: U462.1 Document Code: A Article ID: 1671-7988 (2017)05-01-04

1、引言

倒立擺是一種典型的快速多變量非線性絕對不穩定非最小相位系統。這種控制的方法在航空航天、機器人等領域中都有著廣泛的應用。從控制這個角度上講，對倒立擺的研究在理論和方法上均有著深遠的意義。同時由于倒立擺結構簡單成本低廉因此成為人們學習研究和驗證各種控制理論的理想裝置。

2、一級倒立擺數學建模

直線倒立擺系統是一個機電一體化系統，由小車和擺桿組成。通過同步傳送帶驅動的[2]小車可以在水平方向的導軌上來回移動，位移的大小由固定在導軌的一端的位置傳感器來測量，電機也固定在同一側。擺桿通過轉動鉸鏈與小車相連，共軸角度傳感器安裝在小車和擺桿的連接處，用來測量擺桿轉過的角度。在導軌的兩端裝有控制小車移動距離的開關，當小車到達左右兩端附近的位置時，能夠防止小車脫離導軌起到保護作用。

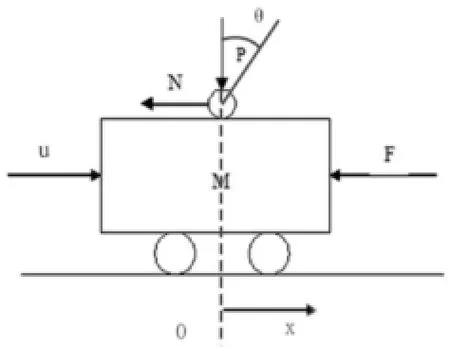
圖1 一級倒立擺小車擺桿位置圖以及受力隔離圖

為了在數學上推導和處理問題的方便，可作出如下假設：

（1）擺桿在運動中是不變形的剛體；

（2）齒型帶與輪之間沒有相對滑動，齒型帶長度保持不變；

（3）小車在移動的過程中，摩擦系數保持不變；

（4）忽略空氣阻力；

基于上述條件假設，可將小車和勻質桿組成的系統模擬代替直線一級倒立擺系統（圖1）。

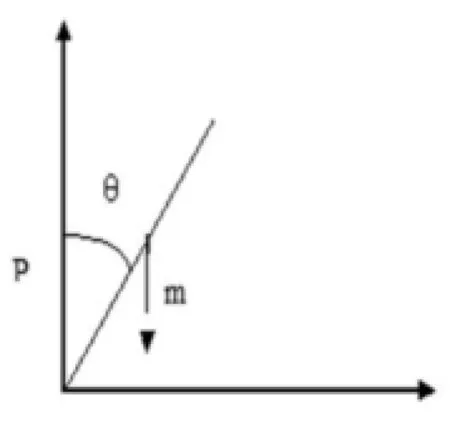
圖2 擺桿受力分析圖

在文中，建立倒立擺的數學模型使用的方法是牛頓——歐拉法。小車和擺桿的相關參數如下所述：

x小車位移，單位(m)；β擺桿與垂直方向的夾角，單位(rad)；M小車的質量，單位(kg)；

m擺桿的質量，單位(kg)；l擺桿的轉動軸心到擺桿質心的距離，單位m；J擺桿對重心的轉動慣量，單位(kg·m2)；u電機對小車施加的作用力，單位(N)；F小車受到的等效摩擦力，單位(N)；

首先，對小車進行受力分析，如圖1和圖2所示。

其中，N和P表示小車與擺桿相互作用力的水平和垂直方向的分量。F為小車受到的作用力，x為小車位移，β為擺桿與垂直向上方向的夾角，θ為擺桿與垂直向下方向的夾角(考慮到擺桿初始位置為豎直向下)[3]。再結合例句平衡方程可以得到系統的運動方程：

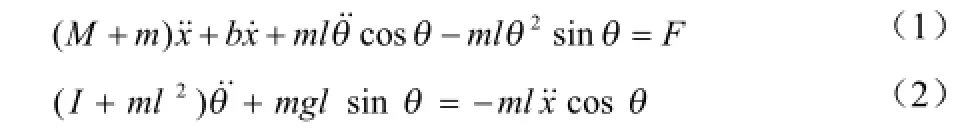
注意：推導傳遞函數時假設初始條件為0。由于輸出角度為Φ，求解方程組(9)得到傳遞函數為：

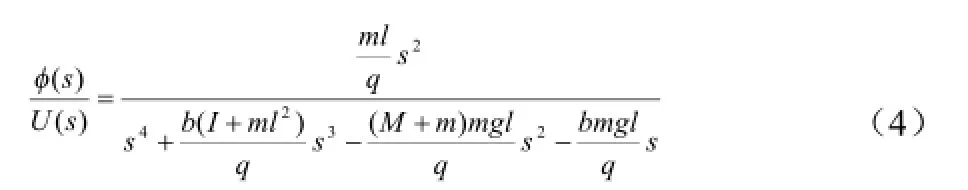
由于系統狀態空間方程表達式為：方程組（5）對x˙˙，θ˙˙解代數方程，得到解如下：

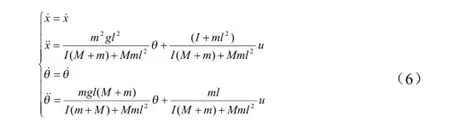
式（6）為直線一級倒立擺系統在平衡點附近局部線性化以后得到的狀態方程。將該式寫成矩陣形式可以得到系統的狀態空間方程為：

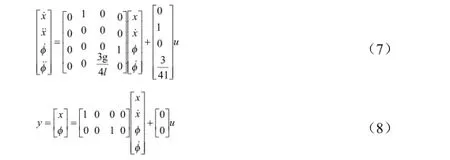
3、PID控制控制算法的設計

PID控制算法和模糊控制、神經網絡控制等相比是一個非常傳統的控制方式。PID控制的優點是應用范圍比較廣，而且參數較易調整。雖然倒立擺模型是非線性的，但通過對其簡化可以變成基本線性的系統。

(1) 比例調節P

比例系數KP的大小決定了比例調節器調節速度的快慢，但KP過大會使控制系統出現超調或振蕩現象，KP過小又起不到調節作用比例控制無法消除余差[4]。

(2) 積分調節I

積分常數Ti大小的選擇決定了積分作用強弱程度，而積分作用一般會導致系統的穩定性下降。

(3) 微分調節D

當偏差e瞬間波動過快時微分調節器會立即產生響應來抑制偏差的變化使系統更趨于穩定改善了系統的動態性能。

首先在Simulink中搭建模型如下圖所示：

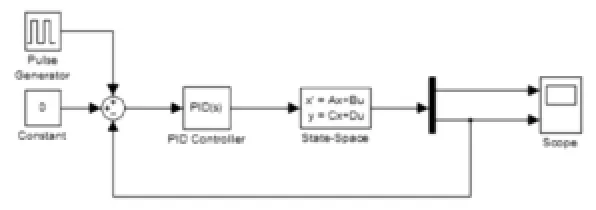
圖3 Simulink模型圖

在上圖中PIDController中根據實際更改PID的三個參數，使小車到達穩定狀態。在狀態空間中根據建立的模型，把實際的系統參數帶入A、B、C、D中，從而確定模型的屬性。

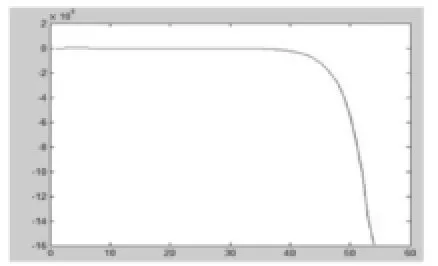
圖4

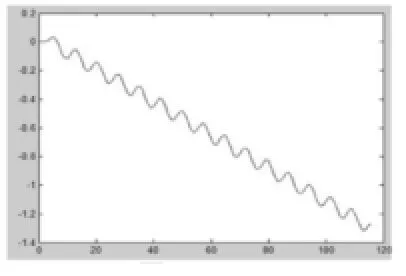
圖5

圖6

圖7

圖4 KP=9, Ki=0, KD=0仿真圖，控制曲線不收斂，需要增大控制量。

圖5 KP=40, Ki=0, KD=0仿真圖，閉環控制系統持續振蕩。為消除系統的振蕩，應增加微分控制參數KD。

圖6 KP=40, Ki=20, KD=4仿真圖，小車的控制基本穩定，角度基本為0度，但是小車的位置在持續的變化，所以小車有穩態偏差。

圖7 KP=40, Ki=20, KD=80仿真圖，相比之下小車的位置穩定性大幅度提高，但是如果要達到絕對的穩定，還應通過以下兩種方法解決：一，繼續調整PID的三個控制參數。二，采用雙PID控制。

因此，采用PID控制可以達到工程上的效果，但是需要反復調整三個控制參數才能達到預期效果。從表面上來看帶有一定的盲目性，因此本文又嘗試結合最優控制的方法。

4、LQR控制算法的設計

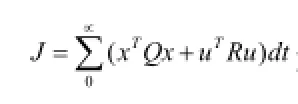
LQR控制器的最優反饋增益矩陣為：

K=LQR（A,B,Q,R）

u(k)=-Kx

由原理知，要求出最優控制作用u，除求解代數Riccati方程外，加權矩陣的選擇也是至關重要的，下面是幾個選擇的一般原則：

① 通常選用Q和R為對角線矩陣,當控制輸入只有一個時，R為標量數。

② Q的選擇不唯一，這表明當得到的控制器相同時，可以有多種Q值的選擇，其中總有一個對角線形式的Q。

下面將通過仿真實驗求加權陣Q、R與性能指標間的關系：

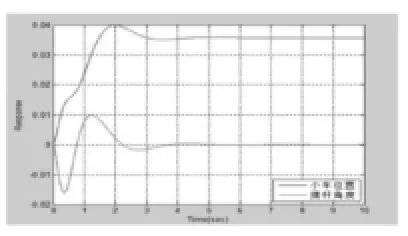
圖8

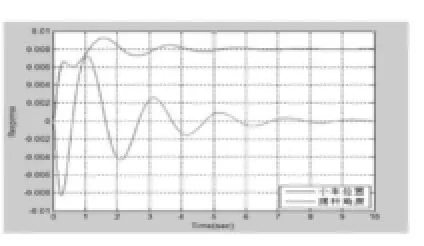
圖9

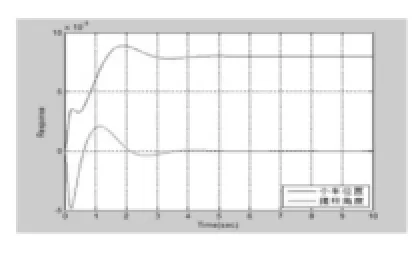
圖10

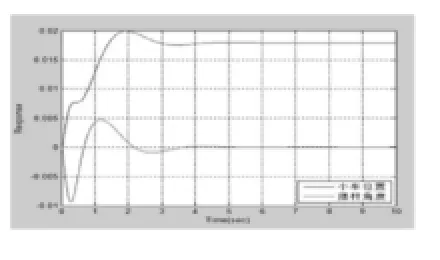
圖11

● 在w11=500、w33=500時，K =22.3607 13.5836 -22.3497 2.2314。小車位置和擺桿角度的關系如圖8所示。

● 在w11=10000、w33=500時，K =100.0000 23.8060 -13.7383 5.8454。小車的位置和擺桿角度的關系如圖9所示。

● 在w11=10000、w33=10000時，K =100.0000 50.1585 -78.6839 19.9598。小車的位置和擺桿的角度如下圖10所示。

由圖8-10可以看出Q矩陣中的權值對系統的穩定時間、超調量和調整時間有很大的影響。在w11=10000、w33=500時，小車的位置和擺桿的角度有很大的超調量，尤其是擺桿角度超調量更大。這對小車的穩定性是很不利的。所以需調整Q中的權值，來減少超調量和調整時間。

通過大量的實際測試，在w11=10000、w33=10000，系統的調整時間變的最短。同時，系統的超調量和穩定時間也有所減少，是一種比較理想的狀況。但是在系統穩定的前期仍然需要調整[7]。

故可得出結論當Q(t)陣中某一元素的權值增大時, 與其相對應的x(t)的動態響應過程好轉, ts、td顯著下降系統快速性得到一定提高；與此同時，也引進了一些振蕩而控制量的幅值會相應增大這表明要求輸入能量增大即要提高動態性能必須以比較大的能量消耗為代價。

現保持Q值不變，即w11=10000、w33=10000,改變R。使R=1變為R=3,考擦控制量的變化，對比仿真結果如圖11所示，K =44.7214 24.5829 -39.8801 7.0549。

可見當R(t)陣中某一元素的權值增大時控制量幅值相應減小由0.8減少為0.5 ,表明能量消耗隨R(t)增大而減小,其對應的動態性能指標有所改善,但并不顯著[8]。

通過上面的分析可知，LQR最優控制系統中Q(t)和R(t)的選擇是相互制約相互影響的，如果要求控制狀態的誤差平方積分減少必然會導致增大能量的消耗反之為了節省控制能量就不得不犧牲對控制性能的要求。

5、結論

常規PID控制的效果相比LQR稍差。主要是因為常規PID控制器實質上是一種線性控制器對于像倒立擺這樣的非線性絕對不穩定系統控制效果上顯得有所不足，但LQR的抗干擾性能及魯棒性也不是十分的完美，因為LQR是通過對系統進行局部線性化后運用的一種方法[9]。

雖然控制理論在不斷的發展新的控制方法不斷的出現，但PID控制器因具有結構簡單設計原理易于被工程設計人員掌握，魯棒性強和不需要對象的精確數學模型等優點在工業過程控制中仍然得到了最廣泛的應用[10]。然而對于那些復雜如具有延遲非線性和時變的控制系統為了克服傳統PID控制的缺點人們把傳統PID控制與模糊邏輯神經網絡遺傳算法等人工智能技術相結合形成智能PID。

[1] 固高科技(深圳)有限公司編著.倒立擺與自動控制原理與實驗[M].2005,24-27.

[2] 關天祥,陳瑋,羅俊奇.一級倒立擺的建模、仿真與實時控制[J].深圳信息職業技術學院學報,2007,2.

[3] 黃苑紅,梁慧冰.從倒立擺裝置的控制策略看控制理論的發展和應用.廣東工業大學學報，2001,19(3)：49-52.

[4] 李曉燕.平面一級倒立擺系統的智能控制策略研究：[碩士學位論文].山西：太原理工大學，2005.

[5] 宋西蒙.倒立擺系統LQR-模糊控制算法：[碩士學位論文].西安：西安電子科技大學,2006.

[6] 陳華龍,梁慧冰,霍迎輝.四級倒立擺的Lagrange方程建模.廣東工業大學學報,2004，21(2)：59-63.

[7] 朱江賓,易建強.二級倒立擺的擺起控制.系統仿真學報.2003,15(7)：1043-1045.

[8] 張錚等編著.MATLAB在控制系統中的應用.北京：電子工業出版社,2007,5.

[9] 朱文凱，袁桂娥，朱學峰.倒立擺的PID與LQR控制算法的對比研究.廣東自動化與信息工程，2006，(2)：1-3.

[10] 吳文進,葛鎖良.基于LQR最優調節器的二級倒立擺控制系統.安慶師范學院學報（自然科學版）,2007,13(2)：32-34.

Design of Single Inverted pendulum based on PID and LQR

Cheng Minghe, Chen Cang

（Changan University, Shaanxi Xi'an 710064）

In this thesis single inverted pendulum model was built. And on this basis, through MATLAB simulation tools, inverted pendulum PID and LQR control algorithm was carried on the design and simulation. In general, the LQR control algorithm is superior to the control performance of PID control algorithm.

Single inverted pendulum; PID; LQR

U462.1

A

1671-7988 (2017)05-01-04

程明賀，（1993-）男，碩士研究生，就讀于長安大學。研究方向：數字圖像處理。