基于MCNP程序的壓水堆不同方式換料后反應(yīng)堆物理分析

徐啟，張弓

(華北水利水電大學(xué) 電力學(xué)院，鄭州 450045)

基于MCNP程序的壓水堆不同方式換料后反應(yīng)堆物理分析

徐啟，張弓

(華北水利水電大學(xué) 電力學(xué)院，鄭州 450045)

換料方式對(duì)反應(yīng)堆的經(jīng)濟(jì)性與安全性起著至關(guān)重要的作用。運(yùn)用蒙特卡羅方法中的MCNP程序建立35 MW小型反應(yīng)堆物理模型，為燃料元件、冷卻劑、堆芯構(gòu)件、反射層建立了精確的物理計(jì)算模型，并對(duì)換料后此堆芯的有效增殖因子(keff)、中子能量分布及中子徑向通量密度分布等物理量進(jìn)行計(jì)算，同時(shí)著重分析計(jì)算堆芯功率密度分布。繪制堆芯功率密度分布三維圖，總結(jié)功率密度分布規(guī)律。通過一系列的物理計(jì)算以及對(duì)數(shù)據(jù)的歸納總結(jié)，為堆芯的物理優(yōu)化以及換料方式對(duì)展平堆芯功率所起到的作用提供了依據(jù)。

微型反應(yīng)堆；換料；蒙特卡羅方法；物理分析；功率計(jì)算

0 引言

核電廠中，一般對(duì)核燃料采用分批裝載的方法來展平反應(yīng)堆功率分布。每次換料時(shí)，只將其中燃耗最深的一批卸出，然后加載相同個(gè)數(shù)的一批新料。核電廠運(yùn)行時(shí)，其主要成本是燃料的費(fèi)用，因此，如何滿足電力系統(tǒng)能量需求的前提下，以及在核電廠安全運(yùn)行的設(shè)計(jì)要求和技術(shù)規(guī)范限制內(nèi)，盡可能地提高核燃料的利用率，降低核電廠的單位能量成本，是一個(gè)關(guān)系到核電廠經(jīng)濟(jì)性的重要研究課題。

壓水堆核電廠換料設(shè)計(jì)[1]是針對(duì)已給出的反應(yīng)堆熱工、水力及機(jī)械設(shè)計(jì)，以前一循環(huán)用戶要求及其所用燃料為依據(jù)，明確載入堆芯燃料的組件數(shù)目、富集度、新燃料以及部分燃耗燃料組件在堆芯的排布方式，計(jì)算換料堆芯性能參數(shù)并進(jìn)行安全評(píng)價(jià)，使反應(yīng)堆功率分布合理并達(dá)到燃耗循環(huán)期要求等預(yù)期的安全要求，令核電廠用戶的能量需求得到滿足。

本文以35 MW微型反應(yīng)堆為研究對(duì)象，建立堆芯MCNP模型，經(jīng)過一系列物理計(jì)算，著重分析其堆芯內(nèi)-外換料、外-內(nèi)換料以及外-內(nèi)分區(qū)交替換料后堆芯中子能量分布、中子通量密度分布及堆芯功率分布，為堆芯的物理優(yōu)化以及不同換料方式對(duì)堆芯功率的展平效果提供了理論依據(jù)。

1 換料設(shè)計(jì)

1.1 微型反應(yīng)堆堆型設(shè)計(jì)

35 MW微型反應(yīng)堆設(shè)計(jì)堆芯中含有2種不同的燃料組件，分別是鈾氧化物燃料(UOX)組件，混合的鈾-钚氧化物燃料(MOX)組件[2]。壓水堆主要參數(shù)見表1。

表1 壓水堆主要參數(shù)

1.2 內(nèi)-外換料設(shè)計(jì)

在這種換料設(shè)計(jì)中，芯部由內(nèi)向外分為3區(qū)，1區(qū)裝載富集度為3.7%的UOX組件，編號(hào)為#4，即在堆芯最內(nèi)區(qū)裝載新料；在第2區(qū)布置燒過1個(gè)循環(huán)的燃料組件，2區(qū)裝載富集度為3.1%的UOX組件，編號(hào)為#5；將燒過2個(gè)循環(huán)的燃料組件布置在最外區(qū)；3區(qū)裝載富集度為2.4%的UOX組件，編號(hào)為#2。堆芯采取內(nèi)-外換料方案，換料時(shí)，把最外區(qū)的燃料組件卸去，靠近中心區(qū)域兩區(qū)的燃料組件依次分別轉(zhuǎn)移到第2區(qū)和邊緣區(qū)，而在中心區(qū)載入新的燃料組件。

1.3 外-內(nèi)換料設(shè)計(jì)

堆芯燃料組件分布如圖1所示。燃料進(jìn)行初始裝載時(shí)，在堆芯內(nèi)沿徑向分布的3個(gè)區(qū)中裝載3種富集度不同的燃料組件。1區(qū)裝載富集度為2.4%的UOX組件，編號(hào)為#4；2區(qū)裝載富集度為3.1%的UOX組件，編號(hào)為#5；3區(qū)裝載富集度為3.7%的UOX組件，編號(hào)為#2。圖1中#3是MOX組件，#1是反射層。堆芯采用外-內(nèi)換料方案，即新裝燃料組件放置在在堆芯的邊緣區(qū)。換料時(shí)，將中心區(qū)燃耗最深的燃料組件卸去，把第2區(qū)燃料組件倒換至中心區(qū)，然后將第3區(qū)的燃料組件倒換至第2區(qū)，最后再將新補(bǔ)充的富集度為3.7%的燃料組件裝入第3區(qū)。

圖1 堆芯燃料組件分布

1.4 外-內(nèi)分區(qū)交替換料設(shè)計(jì)

將富集度為3.7%的UOX組件仍放在堆芯外區(qū)，把已在堆內(nèi)燃耗了1個(gè)和2個(gè)循環(huán)的燃料組件分散交替排列在堆芯內(nèi)部。

2 物理計(jì)算

2.1 蒙特卡羅方法

蒙特卡羅方法是一種以概率和統(tǒng)計(jì)理論方法為基礎(chǔ)的計(jì)算方法。在求解數(shù)學(xué)、物理以及工程技術(shù)等方面的問題時(shí)，為了計(jì)算所求參數(shù)的統(tǒng)計(jì)特征,首先要建立1個(gè)概率模型或隨機(jī)過程的抽樣；然后給出所求解的近似值，用估計(jì)值的標(biāo)準(zhǔn)方差來表示解的精度。蒙特卡羅方法采用隨機(jī)試驗(yàn)的方法求取積分，即將所要計(jì)算的積分當(dāng)成服從某種分布密度函數(shù)f(r)的隨機(jī)變量g(r)的數(shù)學(xué)期望，即

(1)

通過試驗(yàn)，得到N個(gè)觀察值r1，r2，r3，… ，rN。從分布密度函數(shù)f(r)中抽取N個(gè)子樣，將所對(duì)應(yīng)的N個(gè)隨機(jī)變量的值g(r)的算術(shù)平均值

(2)

作為積分的估計(jì)值。

蒙特卡羅方法的誤差為

(3)

式中：Xα為置信度；σ為估計(jì)的均方差；N為抽樣數(shù)目[3]。可見，在一定置信水平下，可以通過添加抽樣數(shù)目或降低均方差來降低蒙特卡羅方法的誤差。在均方差無法有效減小時(shí)，若要誤令差減半，抽樣粒子數(shù)要增加至原來的4倍，這將對(duì)蒙特卡羅方法的計(jì)算效率產(chǎn)生不利影響。

蒙特卡羅方法采用大量的“試驗(yàn)”，跟蹤模擬235U裂變產(chǎn)生的每一個(gè)中子的輸運(yùn)過程，從產(chǎn)生、慢化、擴(kuò)散到被吸收整個(gè)中子的生命歷程，得到統(tǒng)計(jì)性的試驗(yàn)結(jié)果[4]。

2.2 堆芯有效增殖因子(keff)、中子能量分布計(jì)算

當(dāng)使用MCNP計(jì)算堆芯中子輸運(yùn)時(shí)，模擬的輸運(yùn)過程是其中單個(gè)中子的，即1次模擬就是1個(gè)中子從產(chǎn)生到歷史結(jié)束的整個(gè)過程，中子發(fā)生核反應(yīng)是通過概率權(quán)重的方式進(jìn)行記數(shù)的。程序計(jì)算時(shí)采用1/4堆芯幾何模型。

MCNP記數(shù)卡輸出的數(shù)據(jù)若要成為真正的記數(shù)需要經(jīng)過一個(gè)歸一化因子的轉(zhuǎn)換，將一個(gè)功率水平穩(wěn)定的反應(yīng)堆進(jìn)行臨界計(jì)算的歸一化時(shí)，需運(yùn)用以下公式轉(zhuǎn)換

(4)

在本課題中，反應(yīng)堆額定功率P=35MW。經(jīng)計(jì)算每次裂變反應(yīng)所產(chǎn)生的平均中子數(shù)n=2.656，即如果keff=1，每發(fā)生1次裂變需要提供2.656個(gè)源中子(其余的裂變中子都當(dāng)作被吸收或逃逸)。

將N和P代入(1)式，得計(jì)數(shù)結(jié)果的歸一化因子為f=3.054 8×1018n/s，此歸一化源強(qiáng)常數(shù)是MCNP程序在對(duì)該系統(tǒng)進(jìn)行計(jì)數(shù)統(tǒng)計(jì)時(shí)所必不可少的。

利用蒙特卡羅方法對(duì)換料后此堆芯的有效增殖因子keff、中子能量分布進(jìn)行計(jì)算。運(yùn)行程序可得出內(nèi)-外換料后堆芯的有效增殖因子keff=1.148 78；外-內(nèi)換料后堆芯的有效增殖因子keff=1.155 76；外-內(nèi)分區(qū)交替換料后堆芯的有效增殖因子keff=1.121 31。結(jié)果均滿足鏈?zhǔn)搅炎兎磻?yīng)自續(xù)發(fā)生的條件。

內(nèi)-外換料后堆芯能量分布見表2 ，外-內(nèi)換料后堆芯能量分布見表3，外-內(nèi)分區(qū)交替換料后堆芯能量分布見表4。由此可以看出，3種換料方式下中子能量分布情況基本一致。中子份額在不同能量范圍的分布相差較大，份額較大的中子主要集中在0.1～1.0 MeV，1.0～10.0 MeV能量范圍內(nèi)，在低能和高能區(qū)中中子分布比例較大，中間能量的中子份額并不突出。能量為0.1～1.0 MeV的中子數(shù)目最多，說明堆芯中經(jīng)過慢化劑作用良好，使得中子成為易于引發(fā)裂變反應(yīng)的慢中子[5]的效果顯著。

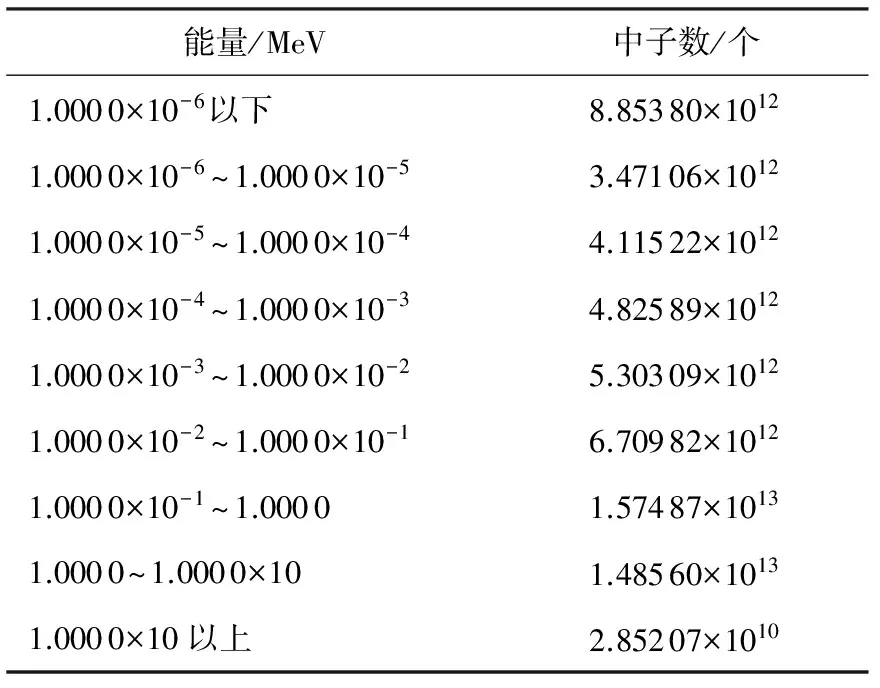
表2 內(nèi)-外換料后堆芯能量分布

表3 外-內(nèi)換料后堆芯能量分布

表4 外-內(nèi)分區(qū)交替換料后堆芯能量分布

2.3 堆芯徑向中子通量分布計(jì)算

中子通量密度指的是單位體積內(nèi)所有中子在單位時(shí)間內(nèi)穿行距離的總和。它是反應(yīng)堆芯內(nèi)核反應(yīng)率的大小的重要參數(shù)，同時(shí)也反映出整個(gè)堆芯的功率水平[6]。使用MCNP對(duì)堆芯徑向柵元內(nèi)中子通量進(jìn)行計(jì)算，在MCNP中，1個(gè)柵元上的平均中子通量需運(yùn)用F4卡來計(jì)算得出[7]。內(nèi)-外換料后堆芯徑向中子通量分布如圖2所示，外-內(nèi)換料后堆芯徑向中子通量分布如圖3所示，外-內(nèi)分區(qū)交替換料后堆芯徑向中子通量分布如圖4所示。

圖2 內(nèi)-外換料后堆芯徑向中子通量分布示意

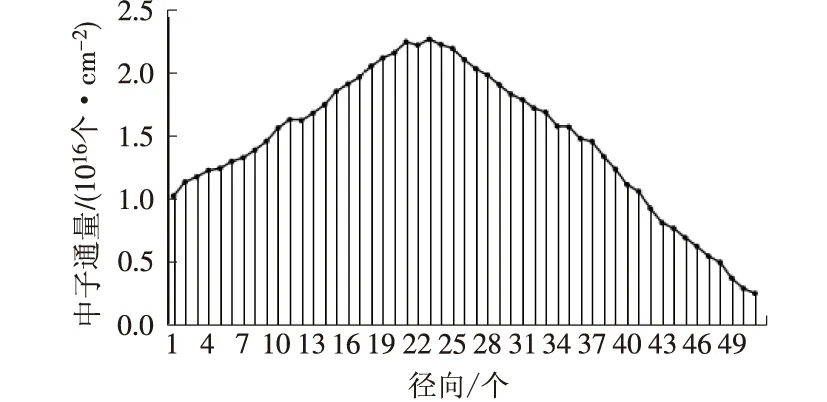
圖3 外-內(nèi)換料后堆芯徑向中子通量分布示意

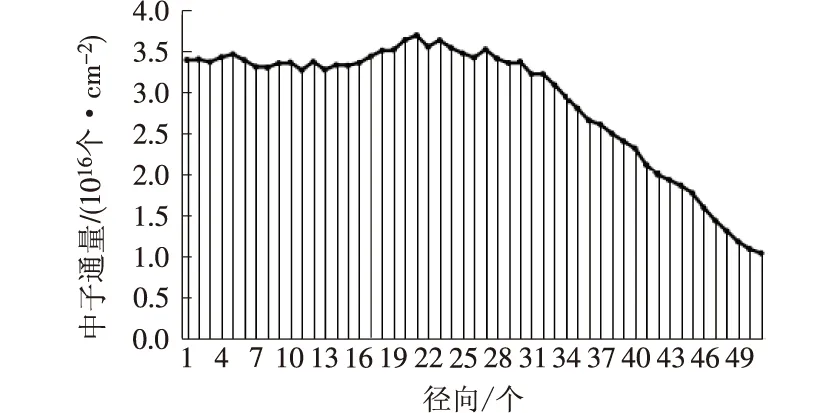
圖4 外-內(nèi)分區(qū)交替換料后堆芯徑向中子通量分布示意

運(yùn)行程序，分析3種不同方式換料后的數(shù)據(jù)可得：堆芯徑向中子通量分布圖從總體上來看，呈現(xiàn)出先上升后下降的趨勢(shì)，這是因?yàn)槎研竟β史逅诘奈恢眉礊橹凶油孔畲笾怠Ｓ啥研局凶油糠植伎梢钥闯觯研竟β史宀⒉皇翘幵诙研編缀沃行纳希俏挥谠诙研編缀沃行耐鈬娜剂蠀^(qū)上；中子通量密度在堆芯坡度最大，在壓力容器區(qū)域較為平緩，變化坡度最平緩的是堆外柵元，越靠近堆芯外圍，中子通量密度越小；外-內(nèi)分區(qū)交替換料方式展平全堆芯的中子通量密度分布效果更為突出，分布將像細(xì)致的波浪形，使得局部功率峰因子大大降低。

2.4 堆芯功率密度計(jì)算

在反應(yīng)堆物理性能評(píng)定中，堆芯功率分布分析是一項(xiàng)關(guān)鍵性工作。在對(duì)于堆芯功率的計(jì)算中，堆芯功率密度分布計(jì)算依舊采取先計(jì)算1/4堆芯，然后經(jīng)過整理，運(yùn)用MATLAB得到其整個(gè)堆芯的平面圖與三維圖。經(jīng)計(jì)算整理，內(nèi)-外換料后堆芯功率分布示意如圖5所示，外-內(nèi)換料后堆芯功率分布意如圖6所示，外-內(nèi)分區(qū)交替換料后堆芯功率分布示意如圖7所示。

圖5 內(nèi)-外換料后堆芯功率分布示意

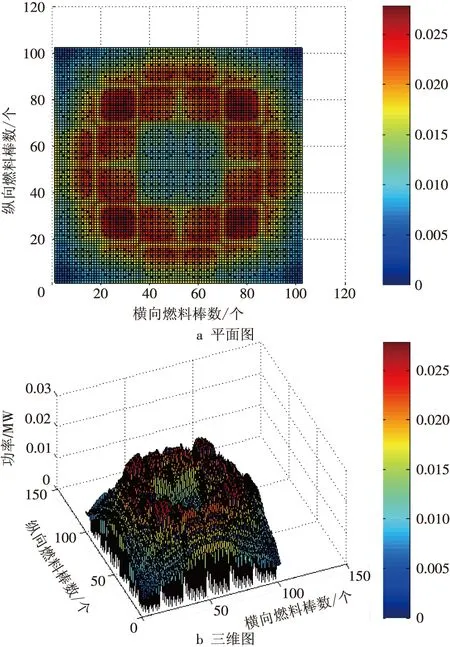
圖6 內(nèi)-外換料后堆芯功率分布示意

圖7 外-內(nèi)分區(qū)交替換料后堆芯功率分布示意

由數(shù)據(jù)及作圖結(jié)果可明顯得出，經(jīng)過不同方式換料后，展平了堆芯中子通量密度分布，從而使功率峰因子下降。在穩(wěn)態(tài)工況下，反應(yīng)堆的功率密度與中子通量密度是成正比的，展平中子通量密度的同時(shí)其實(shí)也就是展平了功率密度，減小了反應(yīng)堆的核熱管因子，從而提高反應(yīng)堆的輸出總功率。堆芯的功率分布與中子通量分布類似，堆芯功率峰并非位于堆芯幾何中心，而是分布在堆芯幾何中心外圍的燃料區(qū)上。

3 結(jié)束語

堆芯換料方法將影響堆芯熱工性能，而堆芯的物理計(jì)算所得參數(shù)又是對(duì)換料方案的檢驗(yàn)與印證。通過MCNP程序?qū)?種不同方式、換料后堆芯的有效增殖因子keff、中子能量分布及中子徑向通量密度分布等物理量進(jìn)行計(jì)算，同時(shí)著重分析計(jì)算堆芯功率密度分布。運(yùn)用MATLAB軟件繪制堆芯功率密度分布三維圖，總結(jié)功率密度分布規(guī)律，綜合評(píng)定了內(nèi)-外換料方案、外-內(nèi)換料方案以及外-內(nèi)交替換料方案。結(jié)果顯示，堆芯徑向中子通量密度分布呈現(xiàn)出壓水堆典型的“雙駝峰”形狀，燃料組件中子通量密度分布比較平坦，趨勢(shì)較為理想，與實(shí)際情況比較契合。從數(shù)據(jù)可以看出，反應(yīng)堆的功率密度與中子通量密度成正比，徑向堆芯功率分布較為平坦，有很強(qiáng)的對(duì)稱性，呈兩端小、中間大的整體分布。

[1]謝仲生.壓水堆核電廠堆芯燃料管理計(jì)算及優(yōu)化[M].北京：原子能出版社，2001.

[2]畢光文,司勝義.壓水堆內(nèi)釷-鈾增殖循環(huán)研究——堆芯設(shè)計(jì)[J].原子能科學(xué)技術(shù)，2012，46(7):791-793.

[3]張建生，蔡勇，陳念年.MCNP程序研究進(jìn)展[J].原子核物理評(píng)論,2008，25(1):48-51.

[4]徐鐘濟(jì).蒙特卡羅方法[M].上海：上海科學(xué)技術(shù)出版社，1985.

[5]謝仲生，鄧力.中子輸運(yùn)理論數(shù)值計(jì)算方法[M].西安：西北工業(yè)大學(xué)出版社，2004.

[6]謝仲生.核反應(yīng)堆物理分析[M].西安：西安交通大學(xué)出版社，2004.

[7]湯曉斌，謝芹，耿長(zhǎng)冉，等.基于MCNP的超臨界水堆堆芯建模及中子通量計(jì)算[J].科技導(dǎo)報(bào)，2012，30(20):41-42.

(本文責(zé)編：劉炳鋒)

2016-10-31；

2017-01-04

國(guó)家自然科學(xué)基金(No.31301586)

TL 351.1

A

1674-1951(2017)02-0016-04

徐啟 (1977—)，男，河南上蔡人，副教授，從事火電廠自動(dòng)控制、信息安全方面的研究(E-mail:hnxuq@ncwu.edu.cn)。