考慮循環溫度影響下注水泥流變性能計算方法

徐璧華， 馮青豪， 謝應權， 楊玉豪

水泥漿的流變性能在固井過程中有著很大的影響[1-2]，然而隨著井深的不斷增加，水泥漿承受的溫度和壓力越來越高，水泥漿高溫、高壓流變性受到的重視也越來越大[3-7]。在以往的研究和現場施工設計中，使用的水泥漿流變性計算方法[8-10]大多都沒有考慮溫度和壓力對水泥漿流變性的影響，而流變參數是注水泥計算的重要參數，如不考慮溫度和壓力對流變性的影響，流動計算將會產生較大誤差，因此對于高溫、高壓下影響水泥漿流變參數的計算，以及流動計算方法的研究具有重要的意義。

1 實驗方案

實驗主要儀器：水泥漿高溫高壓流變性的測試采用美國Chandler公司生產的7400型高溫高壓流變儀。

實驗水泥漿：選取了一種常用的水泥漿，其配方為G級水泥+1%分散劑+5%微硅+2%降失水劑+0.1%消泡劑+水，水灰比為0.44。

實驗條件：實驗選取的溫度為：27℃、 50℃、75℃、 90℃、 120℃、 150℃、 175℃ ；壓力為常壓、20、 40、 60、 80、 100 MPa。

2 溫度、壓力對水泥漿流變性的影響

溫度和壓力對水泥漿流變性能的影響見表1和表2。溫度對水泥漿流變曲線的影響見圖1。

表1 溫度對水泥漿流變性能的影響

表2 壓力對水泥漿流變性能的影響

圖1 水泥漿的流變曲線（壓力60 MPa）

由表1可以看出，溫度對水泥漿流變性能的影響比壓力大得多，隨著溫度的增加，塑性黏度和靜切力明顯下降。由表2可以看出，壓力增加，塑性黏度及靜切力雖有增加，但不明顯。因此，考慮溫度對流體流變參數的影響，是準確設計高溫高壓深井流體流變性的重要影響因素。如應用常溫測量的流變參數，進行高溫高壓深井流變設計，將會帶來比較大的誤差。由圖1可以看出，溫度曲線變化十分明顯，溫度升高，曲線的斜率降低，使黏度減小。

3 考慮溫度影響后流體流變性的計算

3.1 考慮溫度后流體剪切應力計算

通過溫度、壓力流變實驗可看出，鉆井液、水泥漿的流變性要隨溫度發生變化，因此計算各流變模型的流變參數也必須要考慮到溫度的影響。但實際作業時不可能通過實驗方法確定每一溫度壓力下的實際流變曲線，并計算出流變參數。為此，通過大量的實驗數據分析與研究，發現高溫下流體流變性能的變化主要體現為流體剪切應力的變化，從圖1可以看出，剪切應力是以指數形式變化，為此建立了不同溫度影響下的流體剪切應力變化模型，可用下式表示：

式中，τ為任意溫度下的剪切應力；τ0為常溫（或某已知溫度）測定的剪切應力；b為溫度系數。

使用式（1），預測高溫下液體的剪切應力的具體步驟如下：①選取2組溫度，如常溫27 ℃和75 ℃，在不同剪切速率下，測出對應的剪切應力，見表3。②計算溫度系數b。③將b值代入式（1），可以計算出相應剪切速率下，其他溫度的剪切應力值。

表3 旋轉黏度計剪切應力讀值

不同剪切速率下的b值是不一樣的，如預測其他剪切速率情況下，某溫度的剪切應力值，則應按上述方法，先計算溫度系數b值，再計算此溫度的剪切應力數值。

表4是4種不同密度水泥漿不同溫度下，剪切速率為1 022～340.65 s-1測出的剪切應力和應用式（1）、（2）的溫度預測方法，計算出相應的剪切應力的比較結果。

表4 不同溫度下實測剪切應力與推導值的比較（14 MPa）

由表4可以看出，通過該方法計算的不同溫度下， 某一剪切速率的剪切應力， 其總的相對誤差為7.81%， 說明該計算方法可以用來考慮溫度對剪切應力的影響。

3.2 不同溫度下流體流變參數的計算

3.2.1 賓漢流體

用于鉆井液流變參數計算：

用于水泥漿流變參數計算：

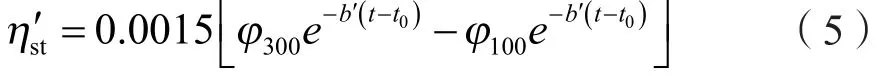
3.2.2 冪律流體

用于水泥漿流變參數計算：

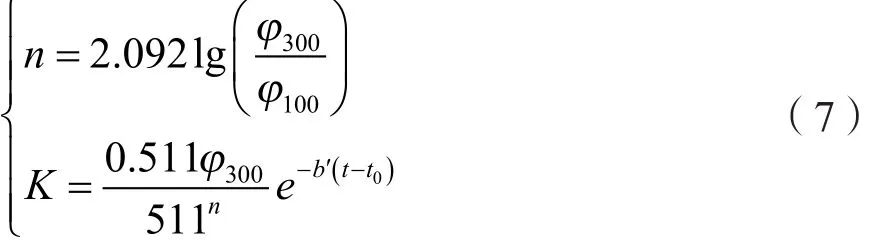
用于鉆井液流變參數計算：

式中，φ600、φ300、φ100為旋轉黏度計在600、300和100 r/min測得的格數；ηst、ηst'為任意溫度下的塑性黏度，Pa·s；τot、τot'為任意溫度下的動切力，Pa；b為剪切速率為1 022 s-1的溫度系數，1/℃；b'為剪切速率為511 s-1的溫度系數，1/℃；b"為剪切速率為170.3 s-1的溫度系數，1/℃。

3.3 考慮溫度后注水泥流動計算方法

分析研究表明，水泥漿的流變性隨溫度壓力變化十分明顯，溫度對流動計算結果的影響非常顯著。水泥漿在不同的溫度下，不僅其流變性能要發生變化，而且其他性能（如水泥漿稠化時間、失水量、自由水等）也要發生變化，有關文獻研究表明，當水泥漿所受實際溫度與進行實驗時的溫度相差5 ℃～10 ℃時，其水泥漿的性能將發生較大變化。

注水泥設計均只考慮井底循環溫度和靜止溫度，這對于保證水泥漿性能，保證施工安全是必要的。對于流動計算，可采用上面介紹的上下水泥面平均溫度來進行簡化計算，但最合理的方法還是按溫度變化分段計算，不過這種計算相當復雜，需使用計算機軟件來實現其應用。

1）分段原則。保證溫度變化在某一范圍，稱為溫度變化限制范圍。該值一般取5 ℃～10 ℃。

2）分段方法。設循環溫度隨井深的變化規律為：

它預測的準確性與地層、井眼、鉆井液、水泥漿的熱導率，施工過程循環排量等眾多因素有關。

該方程建立其反函數式為：

這樣，將循環溫度從井底與水泥面深之間按要求溫度范圍分段后，即可求出相應井深的分段參數。

式中，BHCT為井底循環溫度，℃；TTOC為水泥面深度循環溫度，℃；△T為允許溫度變化范圍，℃；n為井段可分段數；Tm為第m井段底部的循環溫度，℃；Hm：第m井底底部深度，m。如果循環溫度變化函數中沒有包括井斜的影響，則分段時應考慮井斜。

4 現場應用

表5是幾口現場應用井的計算情況，從表中可以看出，考慮分段溫度對流變性影響后其流動摩阻計算結果有所變化，更接近現場實際。

表5 現場注水泥流動摩阻計算

5 結論

LIU Xisheng. Drilling technology principle (Part Ⅱ)[M].Beijing ： Petroleum industry press， 1988.

[2]劉崇建.國外油井注水泥技術[M].成都：四川科學技術出版社，1992：131-141.

LIU Chongjian.Foreign oil well cementing technology[M].Chengdu ： Sichuan Science and Technology Press，1992：131-141.

[3]RAVI K M， SUTTON D L. The relationships of the rheological properties of cement slurries and temperatures[C]. SPE 20449.

[4]王偉，黃伯宗.高溫高壓下水泥漿的流變性及其模式[J].油田化學，1994，11(1)：19-21.

WANG Wei， HUANG Bozong. The rheological properties and model of high temperature and high pressure water mud[J]. Oil Field Chemical， 1994， 11(1)：19-21.

[5]何世明， 劉崇建，鄧建民，等．溫度壓力對水泥漿流變性的影響規律研究[J]．石油鉆采工藝，1999（6）：4-6.

HE Shiming， LIU Chongjian， DENG Jianmin， et al. The influence law reserarch of slurry rhelolgy of temperature and pressure[J]. Oil Drilling Process，1996（6）：4-6.

[6]郭曉陽，劉崇建.非牛頓流體流變模式的研究[J].天然氣工業，1997，17（4）： 43-49.

GUO Xiaoyang， LIU Congjian. Non newtonian fluid rheological model research[J]. Natural Gas Industry，1997，17（4）：43-49.

[7]中華人民共和國石油天然氣行業標準，SY/T5480-92.注水泥流變性設計[S]，第一版.北京：石油工業出版社，1993.

People's Republic of China Oil and Gas Industry Standards， SY/T5480—92. Cement rheological design[S]， the first edition. Beijing ： Petroleum industry press， 1993.

[8]陶謙，周仕明，張晉凱，等. 水泥漿流變性對水平井固井頂替界面的影響——基于天河一號大規模集群計算平臺的數值模擬[J]. 石油鉆采工藝，2017，39（2）：185-191.

TAO Qian， ZHOU Shiming， ZHANG Jinkai， et al.Effect of rheological property of slurry on cementing displacement interface of horizontal well： the numerical simulation based on large-scale cluster computing platform Tianhe-1[J].Oil Drilling & Production Technology， 2017， 39(2)： 185-191.

[9]American Petroleum Institute[S]， API Specification 10，5th edition， Tex-as， U.S.A. 1990.

[10]ERIK B， NELSON. Well cementing[M]. Texas， USA ：Dowell Sohlumberger Educatiaon Service， 1990.