基于計算流體動力學(CFD)的大跨度橋梁風效應數值模擬

程 浩

(廣州地鐵設計研究院有限公司,510010,廣州∥工程師)

基于計算流體動力學(CFD)的大跨度橋梁風效應數值模擬

程 浩

(廣州地鐵設計研究院有限公司,510010,廣州∥工程師)

CFD(計算流體動力學)方法作為風洞試驗的輔助手段,已越來越廣泛地應用于橋梁斷面選型及抗風設計分析中。采用CFD方法,對某軌道交通大跨度橋梁進行了二維流場數值模擬,得到流場的壓力、速度和旋渦分布,還得到了不同高度主梁截面在-3°、0°、3°風攻角時的三分力系數,并對其隨梁高的變化規律進行了分析。

計算流體動力學; 大跨度橋梁; 風效應數值模擬; 三分力系數

在橋梁抗風研究中,風洞試驗一般具有周期長、試驗費用高以及流動可視化困難等缺點,CFD(計算流體動力學)技術的發展為橋梁風工程的研究提供了一種新的手段,節省了大量的人力資源和時間,作為“數值風洞”越來越廣泛地應用于大跨度橋梁抗風設計中,取得了較好的成效。

CFD技術是通過計算機數值計算和圖像顯示,對包含有流體流動和熱傳導等相關物理現象的系統所做的分析,模擬氣流經過橋梁結構時結構周圍的流場分布情況。它可以看作是在流體基本方程(質量守恒方程、動量守恒方程、能量守恒方程)控制下對流動的數值模擬。通過CFD模擬可以得到極其復雜問題的流場內各個位置的基本物理量(如速度、壓力、溫度等)的分布,以及這些物理量隨時間的變化情況,確定壓力分布、速度分布、漩渦分布特征等,還可據此計算出相關的其他物理量。目前,應用數值模擬方法,可較好地計算某些斷面的三分力系數、顫振導數等。隨著越來越多橫跨江河甚至海峽的大跨度橋梁的出現,應用CFD方法研究橋梁氣動性能并應用其指導設計和施工成為必然趨勢。

1 三分力系數

在橋梁風工程研究中,三分力系數是基礎,是抖振響應分析、馳振穩定分析、靜風荷載穩定性分析中的重要參數,其取值直接影響橋梁抗風的精度。根據獲得的三分力系數,可求得作用在橋梁結構上的阻力、升力與扭矩,從而進一步分析橋梁結構在風荷載作用下的應力與位移,并進行穩定性分析。

三分力系數的數值計算原理是:通過對建立的數學模型離散,將微分方程離散為代數方程的形式;對代數方程求解得到計算區域內各節點的速度和壓力,斷面上各點的壓強及摩擦力的合力即為斷面的阻力、升力和升力矩;將三分力無量綱化就得到三分力系數。如圖1所示,在速度為v的流體中橋梁斷面將受到順橋向的力FL和橫橋向的力FD以及流動引起的靜力矩M的作用。

圖1 作用在主梁上的靜力三分力

按體軸坐標系作用于橋梁斷面上的靜力三分力系數為:

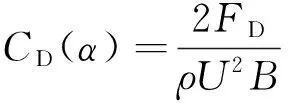
(1)

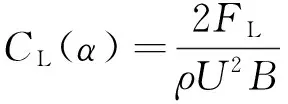
(2)

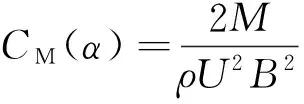
(3)

式中:

ρ——空氣密度;

U——離斷面足夠遠的來流平均風速;

B——結構特征長度;

FD、FL、M——分別為相應的橋梁斷面單位長度上受到的氣動阻力、升力和扭矩。

為計算方便,本文采用二維CFD方法來進行風荷載效應識別。本文中三分力系數的計算是通過FLUENT有限元軟件中2D/3D單精度求解器求解。對于二維模型,通過FLUENT有限元軟件計算出表面的壓力以后,對選定的物體表面的壓力積分可以得到單位長度等截面的三分力值;可根據式1～3計算出三分力系數。對于三維節段模型,為了保證量綱一致,需在式1～3右邊分母上多乘上1個結構特征長度B。

2 大跨度PC箱梁二維流場數值模擬

2.1 工程背景

本文以廣州地區某大跨度軌道交通橋梁為模型,采用FLUENT有限元軟件對不同攻角下主梁斷面的風效應進行了數值識別。如圖2所示,橋梁跨徑布置為60 m+100 m+60 m=220 m。地鐵線路為右側行車的雙線線路,采用1 435 mm標準軌距,雙線橋。列車采用6輛編組,B型車,軸重≤140 kN,設計行車速度120 km/h。上部結構采用單箱單室直腹板箱梁截面,橋面寬12.0 m,梁底寬5.8 m,頂板厚0.3 m,底板厚0.3～1.3 m,腹板厚度0.5～1.0 m,翼緣懸臂長3.1 m,梁高按二次拋物線變化,如圖3～4所示。

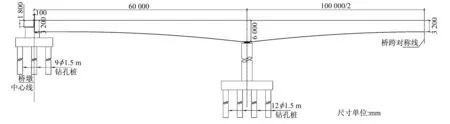
圖2 主橋立面布置

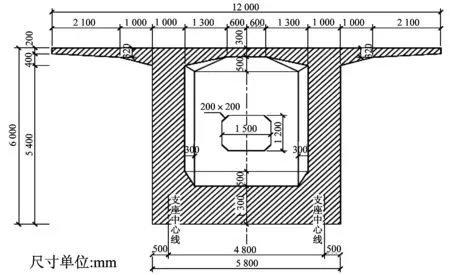
圖3 主梁支點截面

2.2 幾何模擬及計算域的確定

對于箱梁這樣的外部繞流問題,需要定義一個遠離箱梁的邊界,這個邊界與箱梁之間構成流動區域,然后在箱梁與邊界之間劃分網格。為確保箱梁外邊界上的邊界條件與周圍環境基本一致,應將邊界盡量離箱梁遠一些。研究表明入口距迎風面應有5h～6h的距離(h為梁高);模型上下頂面距流域邊界的距離應大于4h;背風面距出口的距離一般要求7h～9h。其次,網格的劃分質量直接影響數值模擬結果的好壞,影響到計算是否收斂。圖5是數值計算時繞主梁跨中截面的網格,流場計算域外邊界均為矩形,計算模型使用1:10比例幾何模型。計算域取值為:入口距迎風面取4倍模型寬度,模型上下頂面距流域邊界的距離取4倍模型高度,背風面距出口的距離取為模型寬度的8倍。整個計算域為15.72 m×2.80 m。在劃分有限元網格時,綜合考慮計算機的計算能力以及計算精度,對內邊界區域網格劃分較密,而外邊界區域網格劃分則適當加粗。通過FLUENT有限元軟件前處理器GAMBIT控制各條邊的尺寸,采用非結構化二維四邊形單元進行網格劃分,整個流場網格尺寸由內向外逐漸增大。

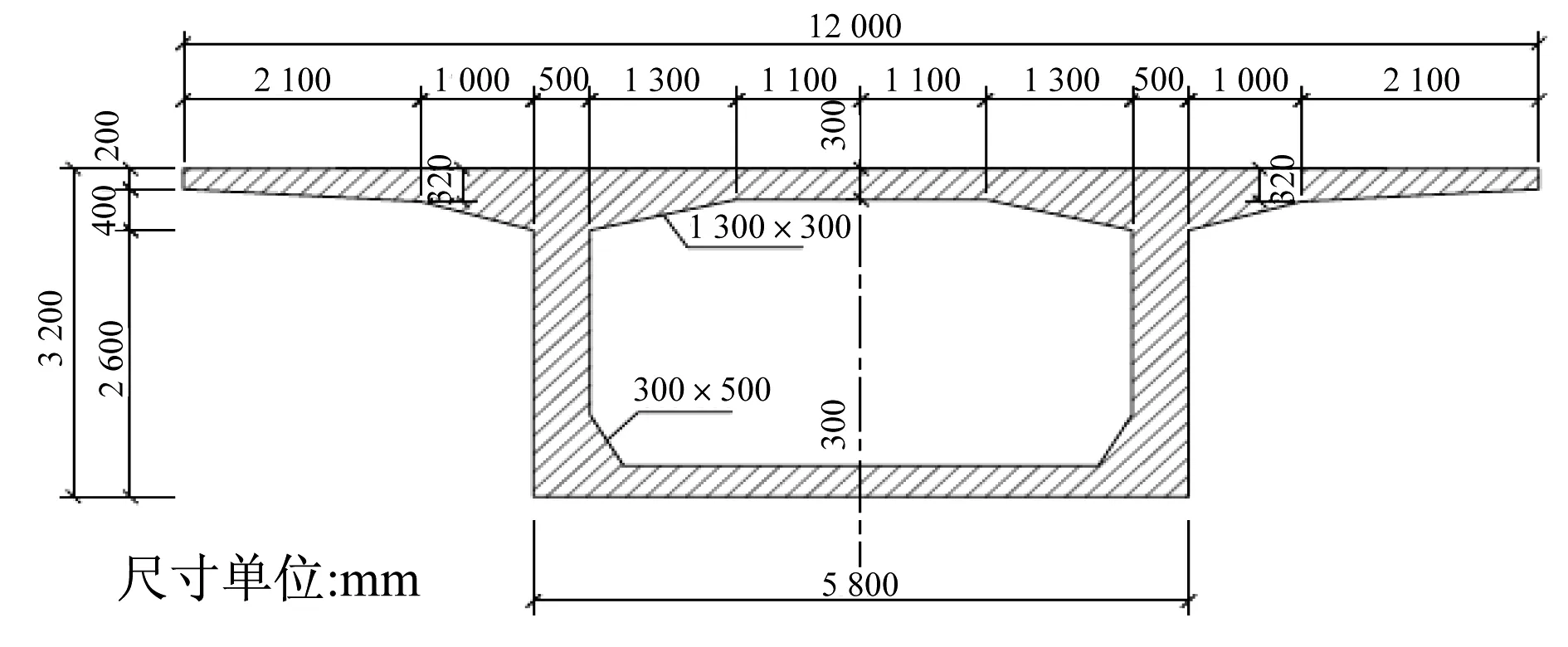
圖4 主梁跨中截面

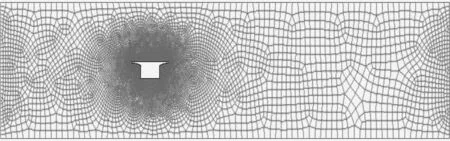
圖5 跨中截面計算網格

2.3 邊界條件及求解參數控制

計算采用二維定常(Steady)分離式求解器(Segregated Solver),選取k-ε兩方程模型的改進型SST湍流模型,湍流強度取0.5%,湍動黏性系數取10。材料采用介質空氣,其密度為1.225 kg/m3、分子黏度系數為1.789 4×10-5kg/(m2s),計算模型的雷諾數為1.54×106。0°攻角來流取入口邊界為20 m/s的速度進口邊界條件(velocity-inlet),出口取表壓為0的壓力出口邊界條件(pressure-outlet),上下邊界及箱梁斷面取無滑移壁面邊界條件(wall);非0°攻角時將上下邊界條件均改為速度進口邊界條件。內邊界的紊流動能和紊流動能耗散率均取0,這樣就真實地模擬了實際橋梁斷面在風環境下的情況。

流場離散化數值解法采用SIMPLEC算法,通過一階迎風差分格式進行離散,待流場計算收斂后獲得流場流態。計算過程中除了監視各控制方程的迭代殘余量外,還需對研究對象的壓力、流場流量等參數進行監視。因為程序默認的控制方程迭代殘余量滿足要求后,流場內的壓力系數可能還會隨著迭代計算的過程發生變化。本文將從三方面對迭代過程進行監視:控制方程迭代殘差應小于指定值(1.0×10-6);橋梁斷面壓力不再隨迭代過程發生變化;通過計算域的流場凈通量(質量等)小于0.1%。當上述條件均滿足要求時,認為流場基本達到穩定。

2.4 流場數值模擬結果及分析

二維流場數值模擬共模擬了來流攻角為-3°、0°、3°情況下3種主梁跨中斷面的流場流態,在流場迭代計算收斂后提取斷面表面受到的三分力及流場流態并保存計算結果。圖6為斷面二維流場數值模擬出的壓強等值線圖。

圖6 -3°、0°、3°風攻角時跨中截面壓強等值線

從圖6可知,跨中斷面在-3°、0°、3°攻角下迎風面為正壓區,上、下表面及背風面均為負壓區。隨著攻角的增大,箱梁上下表面出現了近似圓形的等壓力區,斷面左端部出現來流回旋區,±3°時較小,0°時最大。迎風面與上下表面交接處壓強梯度變化較大,箱梁頂底板上均出現壓力漩渦,且隨著氣流的移動漩渦大小不相同,但形狀相似。從不同攻角下壓強等值線可知,流場在箱梁截面頂、底板處均出現了近似圓形的等壓區,背風面形成渦旋脫落,甚至在翼緣板下游出現了一個較小的尾流漩渦,并隨著氣流的移動顯示出渦流的逐漸脫落。圖7為跨中截面在不同攻角下的速度矢量圖。

從圖7可以看出,流場在迎風側翼緣的尖銳棱角處和梁底的棱角處發生了嚴重的分離。在背風面風速很小,并且形成了漩渦,漩渦形狀會隨著攻角的變化,與來流方向保持一致。在0°攻角背風面出現了一個較大的尾流漩渦,停留在腹板表面附近,遠離渦旋處尾流變窄。

圖7 -3°～3°跨中截面速度矢量圖

3 橋梁斷面形式抗風研究

通過CFD數值模擬計算,可以指導對橋梁斷面進行優化設計。在FLUENT有限元軟件中提取箱梁斷面在體軸坐標系下的靜力三分力,按公式1～3計算即可獲得靜力三分力系數。由式1～3可知,CD、CL、CM與FD、FL、FM分別成正比關系,即CD、CL、CM越大,FD、FL、FM也會越大,箱梁斷面的氣動穩定性也就越差。表1為各斷面在不同攻角下的靜力三分力系數。

表1 主跨各斷面三分力系數

從表1中可知,從跨中到支點隨著梁高的增加,三分力系數的絕對值都有增大的趨勢,而從整體上看,±3°風攻角下箱梁三分力系數絕對值一般要小于0°風攻角下箱梁三分力系數絕對值,這說明梁高越大,對橋梁抗風越不利;箱梁與來流方向有一定的角度,對其抗風越有利。當然,由于計算機模擬也存在誤差,并不是所有的三分力系數絕對值都符合這個規律。三分力系數絕對值越小,在強風作用下,箱梁斷面所受的三分力也就越小,橋梁的抗風穩定性越好。因此,橋梁設計中也多選用低矮、扁平斷面形式。

4 結語

現代橋梁結構向著跨度更大、更柔、更纖細的方向發展,這必然導致對風的敏感性增加,CFD方法作為風洞試驗的輔助手段越來越廣泛地應用于橋梁斷面選型、抗風設計分析中,取得了較好的研究成效與經濟效益。

[1] 項海帆.現代橋梁抗風理論與實踐[M].北京:人民交通出版社,2005.

[2] 譚紅霞,陳政清.CFD在橋梁斷面靜力三分力系數計算中的應用[J].工程力學,2009,26(11):68-72.

[3] 劉鑰,陳政清,張志田.箱梁斷面靜風力系數的CFD數值模擬[J].振動與沖擊,2010,29(1):133-137.

[4] 吳肖俊.高墩大跨連續剛構橋主梁三分力系數數值模擬研究[D].長沙:中南大學,2010.

[5] 瞿偉廉,劉琳娜.基于CFD的橋梁三分力系數識別的數值研究[J].武漢理工大學學報,2007,29(7):85-88.

[6] 孫龍龍.基于FLUENT的典型風區風參數數值模擬研究[D].西安:長安大學,2012.

[7] 黃志淵,陳燊.橋面風環境的數值風洞研究[J].福州大學學報(自然科學版),2007,35(1):95-99.

Numerical Simulation of Wind Effects on Large-span Bridge Based on CFD Analysis

CHENG Hao

As an auxiliary means of wind tunnel test, CFD method is widely used in bridge deck section analysis and wind-resistant design. A large-span bridge of rail traffic is simulated in two-dimensional flow field to get the pressure,velocity and vortex distribution, and the tri-component coefficients of the main beam section when the wind angle of attack is in -3 ° ～ 3 ° at different heights, the variation laws of bridge beam at different heights are analyzed.

computational fluid dynamics(CFD); large-span bridge; numerical simulation of wind effects; coefficient of tri-component

Guangzhou Metro Design & Research Institute Co.,Ltd.,510010, Guangzhou,China

U 442.5+9

10.16037/j.1007-869x.2017.03.017

2014-02-01)