城市軌道交通晚點列車的運行調整模型*
龔 藝 蒲 琪
(同濟大學鐵道與城市軌道交通研究院,201804,上海∥第一作者,碩士研究生)
城市軌道交通晚點列車的運行調整模型*
龔 藝 蒲 琪
(同濟大學鐵道與城市軌道交通研究院,201804,上海∥第一作者,碩士研究生)
分析了城市軌道交通列車發生出發晚點后,在確保安全的前提下,針對不同的初始晚點時間利用運行圖緩沖時間進行運行調整的策略。該策略旨在盡量避免連帶晚點,并使所有受影響列車盡快恢復正點運行。最后建立了列車運行圖的實時調整模型,并運用仿真軟件對策略進行了驗證。
城市軌道交通; 晚點列車; 運行調整策略
城市軌道交通晚點列車是指在執行運行圖過程中發生延誤的列車。列車的晚點運行可分為初始晚點和連帶晚點[1]。初始晚點的發生具有隨機性,所以難以控制,但連帶晚點的影響范圍卻通常可以通過調整運行來減小。本文主要討論列車初始晚點發生后盡快恢復列車按圖行車的調整策略和建立實時的列車運行圖調整模型。
1 運行的調整方法和原則
列車運行的調整方法有趕點運行、壓縮停站時間、小交路、不停站通過、終點站改變折返方式、停運某些列車和使用備車等[1]。在備車不足的情況下,如果不改變列車運行路徑,則可以調整的變量主要是列車的停站時間和區間運行速度。調整時需要滿足發車間隔、運行間隔、到達間隔等運行間隔時間的最小間隔要求,并避免“站外停車”的發生[2]。本文將提出一種充分利用運行圖緩存時間的運行調整策略,列車運行圖中緩沖時間的存在形式如表1所示[3-4]。
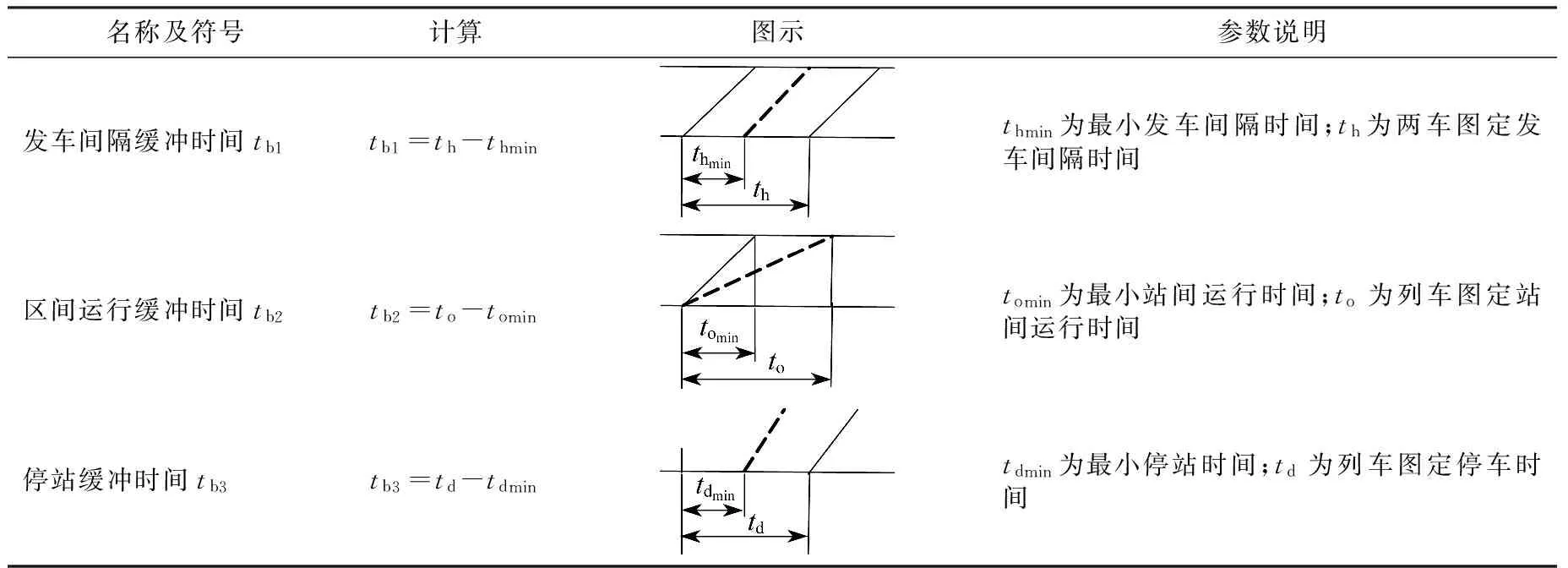
表1 列車運行圖的緩沖時間定義表
當前行列車的晚點時間大于其相鄰后行列車間的緩沖時間時,就會造成相鄰后行列車的連帶晚點。當相鄰后行列車的連帶晚點影響到次相鄰后行列車的運行時,就發生了延誤傳播。計劃運行圖中緩沖時間越大,晚點列車可以調整的余量就越多,延誤傳播的范圍則更容易被控制。
2 晚點列車運行調整策略
當初始晚點發生后,列車運行調整的目標是:盡量減少發生連帶晚點的列車數量,并使發生晚點的列車盡快恢復按圖行車。保障安全的晚點列車運行調整策略即基于上述原則。
2.1 趕點運行
趕點運行是指列車在區間以高于運行圖的速度運行,來縮短列車區間運行時間以抵消一部分初始延誤的運行方式。當列車i在車站j的出發晚點時間ti,j較小時,可通過列車i在下一區間的趕點運行來恢復其正點到達(如圖1所示)。

注:to,i,j+1為列車i在車站j與j+1間的圖定運行時間;tomin,j+1為 列車在車站j與j+1間的最小運行時間;th,i,j為列車i和列車i+1在車站j的圖定發車間隔時間;td,i+1,j——列車i在車站j+1的停站時間
圖1 前行列車站后趕點運行示意圖
列車出發晚點小于車站j和j+1間的運行緩沖時間tb2,j+1,即:
ti,j≤tb2,j+1
(1)
同時,為了不影響后行列車的發車,需要滿足:
th,i,j-ti,j-td,i+1,j≥thmin,j-td,i+1,j
(2)
式中:
thmin,j——列車在車站j的最小發車間距;
式(2)化簡可得:
ti,j≤th,i,j-thmin,j=tb1,j
(3)
因此,式(2)實際意義為列車初始晚點延誤時間不大于發車間隔緩沖時間。
綜上,使用趕點運行策略的條件為:
ti,j≤t1=min(tb1,j,tb2,j+1)
(4)
2.2 “趕點+少停”運行
如果列車i在車站j+1有停站緩沖時間,則還可通過縮短列車i在j+1處的停車時間來盡快使列車恢復按圖行車(見圖2)。
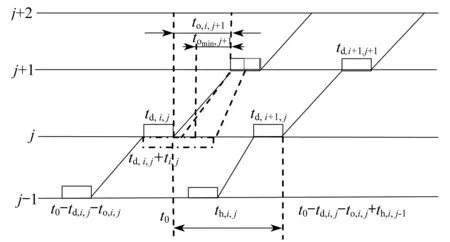
圖2 前行列車站后“趕點+少停”運行示意圖
由圖2可知,列車出發晚點不大于列車在車站j和j+1之間的區間運行緩沖時間tb2,j+1和列車i在車站j+1處停站緩沖時間tb3,i,j+1的和,即:
ti,j≤tb2,j+1+tb3,i,j+1
(5)
同時,為了不影響后續列車的發車時間,ti,j還應滿足ti,j≤tb1,j。因此,ti,j滿足:
ti,j≤t2=min(tb1,j,tb2,j+1+tb3,i,j+1)
(6)
2.3 “趕壓+少停”運行
當列車i初始出發晚點延誤時間大于發車間隔緩沖時間時,一定會影響后續列車。此時應采用前行列車“趕點+少停”運行、后行列車“壓點”運行的調整方法(如圖3所示)。其中,“壓點”運行是指以低于列車運行圖計劃的速度運行,保持安全追蹤距離的運行方式。
注:ta,i+1,j,為列車i+1到達車站j的到達晚點時間
圖3 前行列車“趕點+少停”運行、后行列車“壓點”運行示意圖
延長相鄰后行列車i+1在站間的運行時間,將縮短列車i+1與列車i+2的追蹤間隔,為減小對后續列車的影響,列車i+1應該以保障安全的最大速度vmax行駛。則有:
(7)
式中:
vl——列車當前位置的線路限速;
s——前后車之間的距離;
ab——列車制動的最大減速度。
列車i在車站j+1的發車延誤時間ti,j如圖3所示,則列車i+1的發車延誤時間為:
ti+1,j=[thr,i,j+(td,i,j+ti,j)]-(td,i,j+th,i,j)
(8)
其中,thr,i,j為列車i和i+1在車站j的實際發車間隔時間,且thr,i,j滿足:
(9)
式中:
td,i+1,j——列車i+1在車站j的圖定停站時間;
tdmin,j——列車在車站j的最小停站時間。
另外,為不延誤列車i+2及其后續列車
ti+1,j≤tb1,j+1
(10)
根據式(9)、(10)和(11)可得:
ti,j≤tb1,j+1+min(tb1,j,tb3,i+1,j+ta,i+1,j)
(11)
根據圖3,要使列車i在車站j的發車延誤不影響列車i+1在車站j的發車,則發車延誤時間ti,j+1應滿足:
ti,j+1=ti,j-t2≤tb1,j+2
(12)
從而得到初始延誤時間:ti,j≤t2+tb1j+2。
綜合上述分析,ti,j應滿足:
ti,j≤t3=min(tb1,j+1+min(tb1,j,tb3,i+1,j+
ta,i+1,j),t2+tb1,j+2)
(13)
根據以上策略,可求出列車在區間的運行時間。在已知區間運行時間的情況下,即可使用基于極小值原理的最優控制求解最小能耗下的運行曲線[5-8],最終得到運行調整的算法流程(見圖4)。
3 列車運行圖的實時調整模型
列車運行圖反映了列車運行的時間和位置的關系。將列車運行圖中關鍵數據提取出來,可形成1個時間矩陣(單位為s)。利用這個矩陣即可實時分辨列車運行情況并進行相應調整。列車運行計劃的調整實質上是對列車運行圖的重新鋪畫。
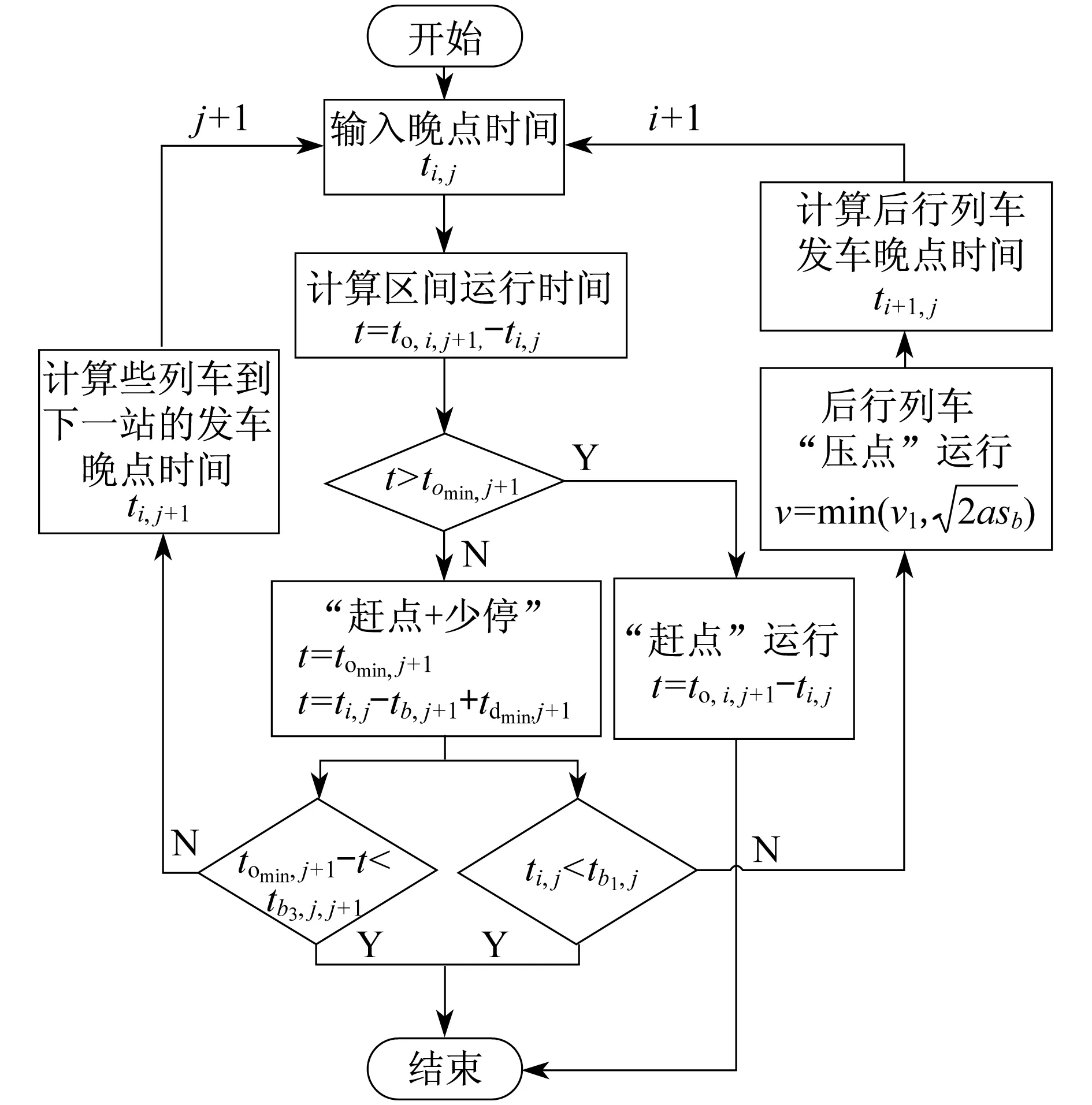
圖4 運行調整的算法流程圖
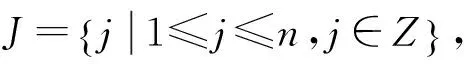
運行調整后,各列車在車站的出發時刻xd,i,j∈Xd,到達時刻xa,i,j∈Xa,停站時間xs,i,j∈Xs。
3.1 建立模型
3.1.1 約束條件
(1) 變量取值范圍約束。列車在車站的到達和出發時間應該在運營時間ts范圍內。即:
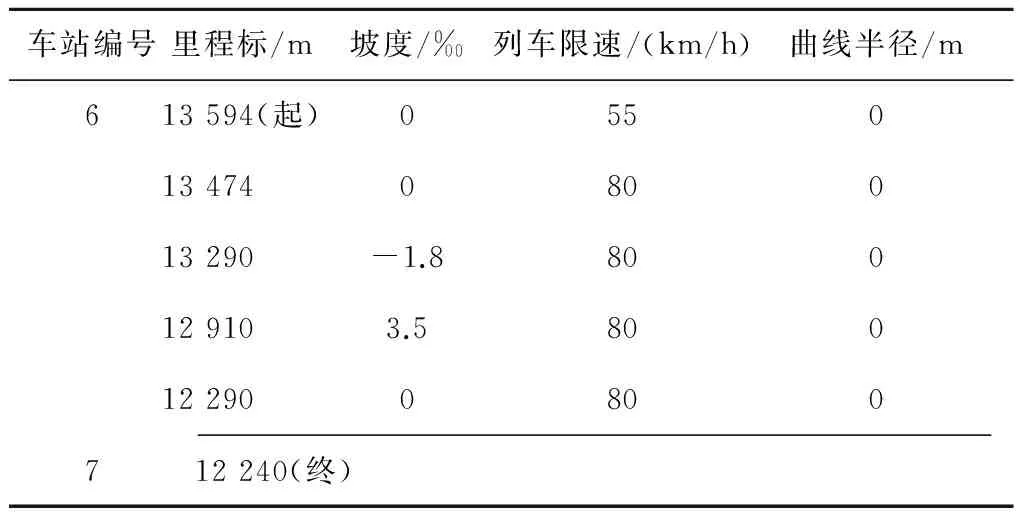
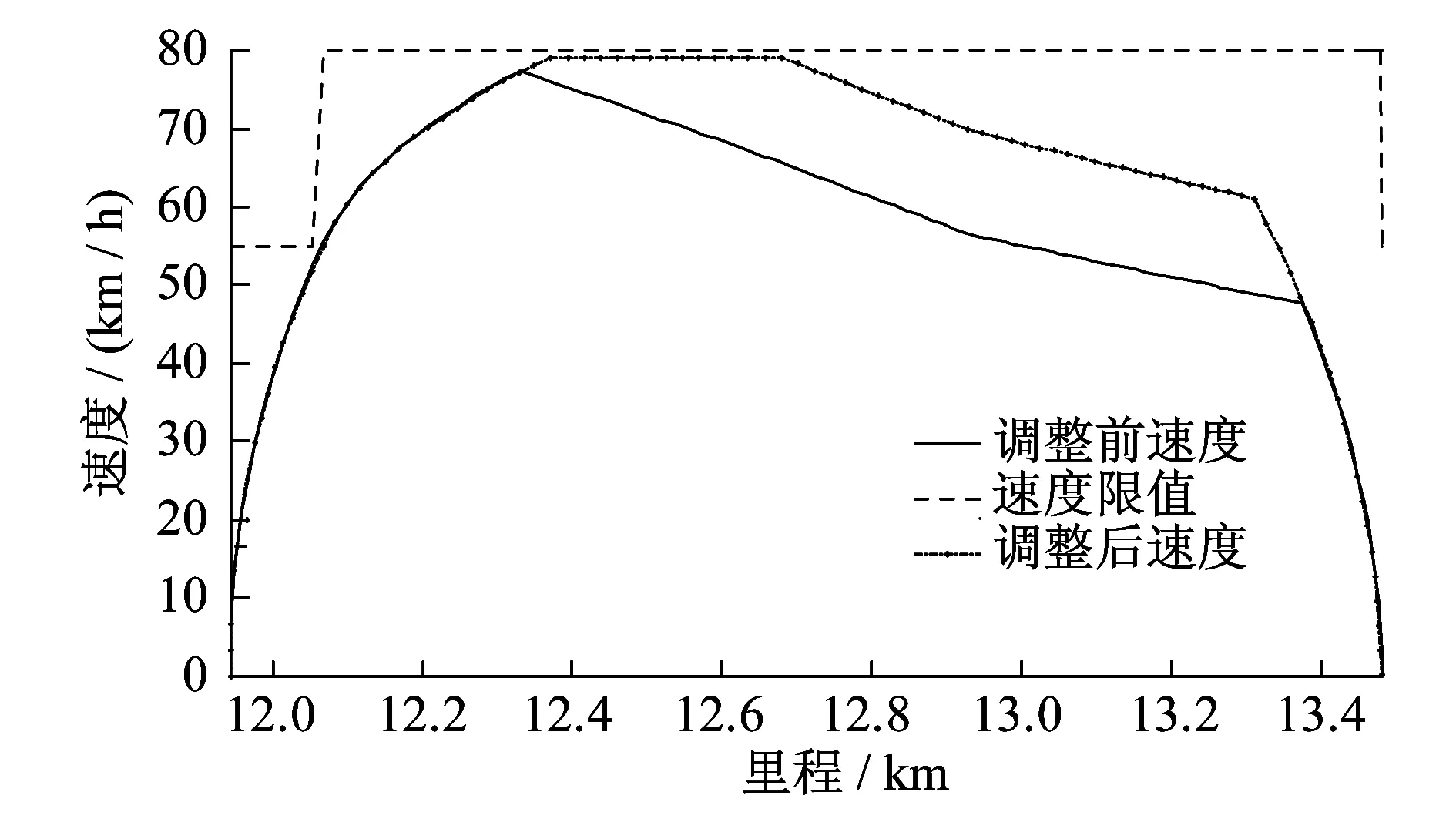
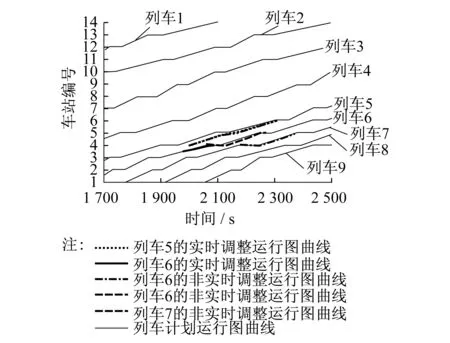
xd,i,j (14) xa,i,j (15) (2) 列車出發時間約束。列車在車站的出發時間不能早于原計劃出發時間。同時,運行調整后,中途各站出發時間不能早于到站時間,即: xd,i,j≥Cd,i,j (16) xd,i,j≥xa,i,j (17) (3) 最小運行間隔時間約束。發車間隔及運行間隔及到達間隔等最小運行間隔時間約束已經包含在調整策略中,這里不再贅述。 3.1.2 優化目標 運行調整的目標是使發生列車晚點到所有列車恢復按圖行車所經歷的時間最短,并盡量避免連帶晚點。如果列車i在車站j發車晚點時間為ti,j,則優化目標為: (18) 式中: xa,α,β——調整后,當列車α到達車站β(α∈I,β∈J)時,全部列車均恢復按圖行車的時刻。 3.1.3 仿真調整流程 首先,需構造運行圖的時間矩陣,將日計劃運行圖中列車在各站的xd,i,j、xa,i,j、xs,i,j的數據提取出來,構成了運行圖的時間矩陣。利用計算機每隔1 s采集列車實時運行的變量(xd,i,j,xa,i,j,xs,i,j)信息,并將其與運行圖的時間矩陣中對應的數據對比。如兩者不同則開始調用相應的調整策略,直至后續時刻的變量數據與時間矩陣中數據相同為止。算法流程見圖5 。 圖5 實時運行調整流程圖 3.2 算例分析 選取某線路數據作為計算對象,該線路共14個車站,區間總長度為22.9 km。假設列車i在車站6發車晚點,晚點時間ti,6=10 s。車站6到車站7的線路數據如表2所示。 表2 某線路從6號車站到7號車站的線路數據 按照高峰時段的列車運行圖,已知列車由車站6到車站7的圖定運行時間為to,i,7=110 s,列車i和列車i+1在車站6的圖定發車間隔為th,i,6=137 s。調用調整策略得到調整前后列車的運行曲線如圖6所示。 圖6 調整前后列車在車站6至車站7區間的運行曲線 分析可知,初始發車晚點時間滿足ti,j≤min(tb1,j,tb2,j+1)=17 s,應使用“趕點”策略,使列車可準時到達車站7且其后行列車不受影響。列車恢復按圖發車經過的時間為Δt=(xa,i,7-xd,i,6)+ti,6=120 s。由圖6可知,運行曲線與分析結果一致,因此調整策略有效。 以上述線路作為研究對象,假設列車5在車站4初始發車晚點時間為50 s,來驗證列車運行圖的實時調整模型。調整前后的運行圖見圖7。 由調整后的運行圖可以看出,實時調整模型對初始晚點列車的運行調整沒有明顯的改善效果。但是,實時調整模型可比非實時調整策略更早地進行調整,減小了對后續列車的影響。列車運行圖調整結果對比見表3。 圖7 調整前后部分列車的運行圖 城市軌道交通列車發生出發晚點時,可充分利用列車運行圖緩沖時間進行調整。調整策略中,不同初始晚點時間對應3種運行調整方式,即“趕點”、“趕點+少停”和“趕壓+少停”。算例結果表明運行調整策略正確。在此策略的基礎上建立了實時調整模型,其仿真結果表明,實時調整模型能更早地進行運行圖調整,從而減小初始晚點對后續列車的影響。 表3 列車運行圖調整結果對比表 [1] 史豐收,陳斯衛.地鐵列車晚點分析與控制[J].都市快軌交通,2008,(1):41-43. [2] 吳洋.晚點情況下地鐵列車實時運行調整及速度控制模式研究[D].成都:西南交通大學,2004. [3] 江志彬,徐瑞華.城市軌道交通列車運行延誤調整的仿真算法研究[M].北京:中國鐵道出版社,2005:133-139. [4] 彭其淵,朱松年,閻海峰.列車運行圖可調整度評價系統研究[J].西南交通大學學報(自然科學版),1998(4):9-13. [5] 劉煒.城市軌道交通列車運行過程優化及牽引供電系統動態仿真[D].成都:西南交通大學,2009. [6] 石紅國.列車運行過程仿真及優化研究[D].成都:西南交通大學,2006. [7] 李明亮.基于模塊化設計方法的城市軌道交通牽引計算軟件研制[D].北京:北京交通大學,2008. [8] CHENG J X,HOWLETT P G.Application of critical velocities to the minimisation of fuel consumption in the control of trains[J].Automatic,1992,28:165-169. Operation Adjustment Model for the Delayed Urban Mass Transit Train GONG Yi, PU Qi The operation adjustment strategy for the delayed urban mass transit train after departure is analyzed on the premise of safety. By making full use of buffer time in train operation diagram, the strategy for different train delays can make the operation of all trains on schedule in the shortest possible time. Finally, a real-time adjustment model of the train operation diagram is established and verified by the matlab. urban mass transit; delayed train; operation adjustment strategy Institute of Railway and Urban Rail Transit,Tongji University,201804,Shanghai,China *國家科技支撐計劃項目(2015BAG19B01);上海市科學技術委員會項目(15DZ1204304) U 292.4+5 10.16037/j.1007-869x.2017.03.007 2016-06-08)
4 結語