材料力學在力學學科及工程實際中的應用

王神龍

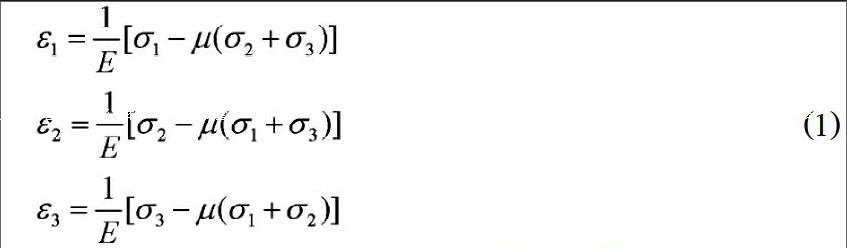
摘 要 材料力學是力學及機械、土木等相關專業的基礎學科，其主要任務是研究桿狀材料的強度、剛度和穩定性。本文重點探討材料力學在其他力學學科，包括彈性力學、板殼力學及振動力學等學科中的應用。此外，還介紹了材料力學在工程實際中的應用。這不僅能深刻闡明學習材料力學課程的意義，還通過實例及工程背景來加深學生的印象，提高教學效率。

關鍵詞 材料力學 彈性力學 板殼力學 振動力學 工程應用

中圖分類號：O31 文獻標識碼：A DOI：10.16400/j.cnki.kjdks.2017.02.024

Abstract Material mechanics is the basic discipline of mechanics and mechanical， civil engineering and other related major， its main task is to study the strength， stiffness and stability of the rod material. This paper focuses on the mechanics of materials in other disciplines including mechanics， elastic mechanics， applied science shell mechanics and vibration mechanics in. In addition， the application of material mechanics in engineering practice is introduced. This can not only clarify the significance of learning material mechanics course， but also through examples and engineering background to deepen the impression of students， improve teaching efficiency.

Keywords material mechanics； elastic mechanics； shell mechanics； mechanics of vibration； engineering application

0 引言

材料力學①是研究桿狀材料的強度、剛度及穩定性的學科，也是力學、機械工程、土木工程等專業的必修課程。該學科的應用范圍非常廣，不僅能解決一些強度校核、穩定性驗證問題，還與其他力學學科，例如彈性力學、②板殼力學③和振動力學④等的交叉非常普遍。此外，材料力學在工程實際和生活中的應用也非常多。本文就通過材料力學在力學學科及工程實際中的應用這兩部分來進行說明。

1 材料力學在力學學科中的應用

1.1 材料力學在彈性力學中的應用

彈性力學是研究彈性體在外力作用、溫度變化及支座沉陷等外部因素作用下產生的應力、應變、位移的一門學科。其研究對象、基本假設及研究方法與材料力學不同，且它的基本研究思路是基于平衡方程、物理方程和幾何方程。其中，彈性力學中物理方程的推導與材料力學息息相關，如圖1所示，根據廣義胡克定律，容易得到

式（1）中，€%l1，€%l2和€%l3分別是材料力學中的第一、第二及第三主應力，E和€%e分別為彈性模量和泊松比。材料力學在彈性力學中的應用還有很多，例如平面應力問題和平面應變問題的區分、應力集中現象在彈性力學中的推廣、圣維南原理、利用切應力來求解彈性力學問題等等，此處不再一一贅述。

1.2 材料力學在板殼力學中的應用

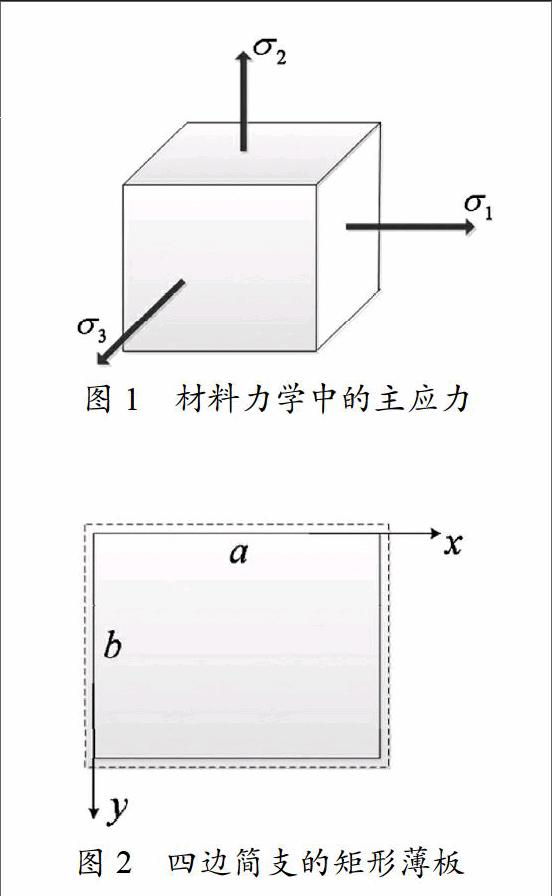
板殼力學是研究工程中的板殼結構在外力作用下的應力分布、變形規律和穩定性的學科。其主要研究內容為薄板彎曲理論以及經典解法、薄板穩定問題、薄殼一般理論。板殼問題的求解過程中，通常會用到材料力學撓曲線方程的微分關系，例如，1820 年，Navier 首先成功求解了均布荷載作用下的簡支矩形板的撓度問題，如圖2中，四邊簡支矩形板的邊界條件為

其中，撓曲線的曲率等于0，即是利用了材料力學中簡支端的彎矩M=0的概念。此外，該方法求解簡支矩形板的撓度，還利用了材料力學中的力法及位移法建立方程，且最終得到板的最大撓度發生在矩形的中心位置，即=a，=b處，這也與材料力學中簡支梁中心位置處撓度最大的概念相符。

1.3 材料力學在振動力學中的應用

振動力學是研究機械振動的運動學和動力學的一門學科。固有頻率的計算，是振動研究重點關注的問題之一。而利用柔度法求解系統固有頻率時，材料力學的應用可以讓問題大為簡化。如圖3所示為一帶有質量塊的懸臂梁，為得到系統的固有頻率，可以將梁等效為彈簧，列振動方程進行求解，然而該方法比較復雜。此處，可以根據材料力學中集中力作用下懸臂梁自由端的撓度公式得到梁的柔度，從而可以進一步得到系統的剛度和固有頻率，讓計算和推導過程簡單化，基本計算過程如下：

類似地，還可以將材料力學中彎曲變形的概念應用于振動測試當中。如圖4（a）、（b）表示用力錘法測試固支梁固有頻率和阻尼比的振動測試實驗及其原理圖。其中，實驗構件由四根兩端固支梁和兩塊矩形鋼板組成，用力錘敲擊矩形板的側面，測試出的系統固有頻率即為四根固支梁的振動頻率。將系統看成四根并聯的彈簧，由材料力學知識，單根兩端固支梁的剛度為： 其中，E為彈性模量，I為慣性矩，L為固支梁的長度，系統總剛度即為 = 48EI/L3，再根據 = ，即可求解出系統的理論固有頻率，并將其與振動測試設備得到的固有頻率相比較，便能驗證該實驗的精確性。

2 材料力學在工程實際中的應用

除了在彈性力學、振動力學等力學學科和專業課程以外，材料力學在工程實際和現實生活中的應用也非常廣泛。例如，如圖5利用有限元軟件分析結構的強度，其中，材料的屬性：包括彈性模量、泊松比等都需要參考材料力學的內容，且分析結果的正確性及其精度，也都可以通過材料力學的理論分析予以證明。在數控機床強度分析、大型自然通風冷卻塔的優化設計中，通常會涉及材料力學的基本概念。

此外，如圖6（a）所示，法國著名景點埃菲爾鐵塔的形狀，也可以利用材料力學中彎曲內力的概念予以解釋。由于鐵塔水平風向通常僅受到水平方向風力的作用，因此從單個方向上可以將其等效為懸臂梁受水平風載作用，其在均布載荷作用下的彎矩圖如圖6（b）所示。越靠近地面，彎矩越大，要保證結構的強度，對建筑物的尺寸要求就越高。再考慮塔身自重以及不同高度和不同季節情況下風速的差別等原因，才最終確定了埃菲爾鐵塔的形狀。巧妙利用了材料力學中彎矩的概念對建筑結構進行優化設計，這也是它與其他塔型建筑物的最顯著區別。

最后，在日常生活中接觸到的包裝袋會有鋸齒形狀或者小孔裂縫，方便與人們撕開，這就用到了材料力學中小孔或者縫隙處會發生應力集中的現象。此外，在汽車、船舶等交通運輸工具中，通常會有材料拼接，拼接處由于材料不同，剛度出現急劇變化，此時也會發生應力集中現象，因此，一味增加此處材料厚度往往會適得其反。這些也都是材料力學在工程實際或現實生活中的應用。

3 結束語

隨著工業4.0概念的普及，高校教育越來越偏重于信息化、智能化，對學生的要求是理論聯系實際、知識用于實踐。本文通過介紹材料力學在力學學科及工程實際中的應用，既可以激發學生對材料力學的興趣、提高課程的教學效率，又能讓學生真正了解材料力學的工程背景和實用價值。

注釋

① 劉鴻文.材料力學（第三版）[M].北京：高等教育出版社，1992.

② 徐芝綸.彈性力學上冊（第四版）[M].北京：高等教育出版社，2006.

③ 徐芝綸.彈性力學下冊（第四版）[M].北京：高等教育出版社，2006.

④ 謝官模.振動力學（第二版）[M].北京：國防工業出版社，2011.