基于SIP-DSWP系統的透明玻璃面傾角分區標定偏振測量方法

溫仁杰，魯嘯天，金偉其，劉 敬，王 霞，郭 宏

?

基于SIP-DSWP系統的透明玻璃面傾角分區標定偏振測量方法

溫仁杰，魯嘯天，金偉其，劉 敬，王 霞，郭 宏

（北京理工大學 光電學院，光電成像技術與系統教育部重點實驗室，北京 100081）

由于存在邊緣視場的漸暈效應，造成SIP-DSWP同時偏振成像系統的偏振信息重構存在偏差。為此，本文提出了一種通過分區儀器矩陣校正視場邊緣效應的成像系統校正方法。通過對SIP-DSWP同時偏振成像系統3×3分區儀器矩陣的標定，進行了玻璃平板傾角的非接觸檢測實驗。實驗結果表明：圖像邊緣視場效應和噪聲能夠直接影響偏振成像及偏振信息（偏振度和偏轉角）重構；分區儀器矩陣較平均儀器矩陣能夠更準確地重構出目標場景的偏振信息，提高對透明玻璃平板傾角的檢測精度，為后續偏振成像方法的研究和定量檢測應用奠定了理論基礎。

同時偏振成像系統；斯托克斯矢量；偏振信息；分區儀器矩陣

0 引言

當透過透明異質界面成像時，物空間的成像系統和目標場景分別位于不同介質中。由于兩種介質折射率的不同，介質交界面的不規則面形會導致成像系統的圖像降質和扭曲，機載水下目標成像、水下物體測量、透過壓花玻璃成像等都屬于此類成像模式。為了實現對透明異質界面成像的圖像復原，需要有效的透明物體面形測量方法。

1982年，RMA. Azzam利用了一塊分光片和兩塊渥拉斯頓棱鏡的組合將測量光束分為不同的四束光，并用四組探測器對四束光進行探測，從而獲得了測量光束的偏振信息。目前國內外已根據偏振成像技術提出一些校正水下降質和扭曲圖像的方法[1]。偏振成像技術利用光電成像器件獲取景物輻射或反射信息進行成像，不僅可獲得景物的光強度分布，而且能夠獲得景物偏振度、偏振角、偏振橢率等參數信息，增加目標探測和場景理解的可用信息[2]，對透明介質面形的測量展現出技術可行性，可用于透明介質（諸如玻璃、水面波紋）面形的偏振成像測量。2008年由美國哥倫比亞大學地球觀測站、澳大利亞新南威爾士大學、美國馬薩諸塞大學以及美國紐約春分公司組成的研究小組提出了一種基于偏振成像方法測量水面短波紋二維傾角的偏振傾角測量方法PSS（Polarimetric slope sensing）[3-4]，利用白天無偏的天空光作為入射光，通過偏振分光成像系統獲取入射光和反射光偏振角的關聯，從而推斷出視場中圖像的瞬時二維偏振度和偏振角。2009年馬薩諸塞大學Schultz Howard 等獲得美國發明專利“透過不規則水面成像的系統和方法”[5]，通過偏振測量獲得水面幾何結構，進而利用其去除海面起伏時引起的圖像扭曲。2016年劉敬等研究了考慮探測器特性的光電偏振成像信息重構方法[6]，證明通過儀器矩陣標定，可消除SIP-DSWP（Simultaneous Imaging Polarimetry with Double Separate Wallaston Primes）同時偏振成像系統[7]探測器g校正系數的影響。但由于在整個偏振成像幅面上偏振光學系統往往存在漸暈等影響，使得采用視場中心標定單一儀器矩陣難以適應全畫幅視場的校正。為此，本文將分析SIP-DSWP同時偏振成像系統的基礎上，研究采用分區儀器矩陣的方法，以減小系統校正的誤差，提高透明介質的三維面形檢測的精度。

1 SIP-DSWP同時偏振成像系統原理

1.1 理想偏振光學系統的儀器矩陣

光波偏振特性可表示為一個4×1的斯托克斯[8]矢量：

＝[]

式中：表示總光強；和分別表示線偏正分量；表示圓偏振分量。用穆勒矩陣描述光學元件對光波偏振態的改變：

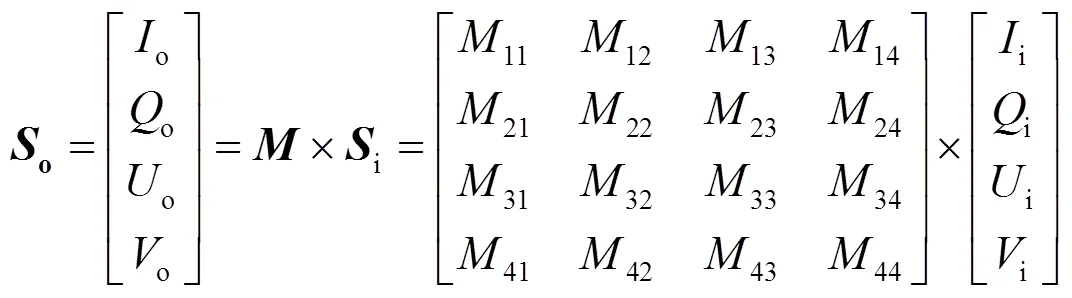
式中：i和o分別為入射光和出射光的斯托克斯矢量；表示光學元件/系統的穆勒矩陣。

對于四通道同時偏振成像系統，入射光的i經過偏振分光元件到達同時偏振成像系統4個子通道探測器的光強(1)、(2)、(3)和(4)滿足：

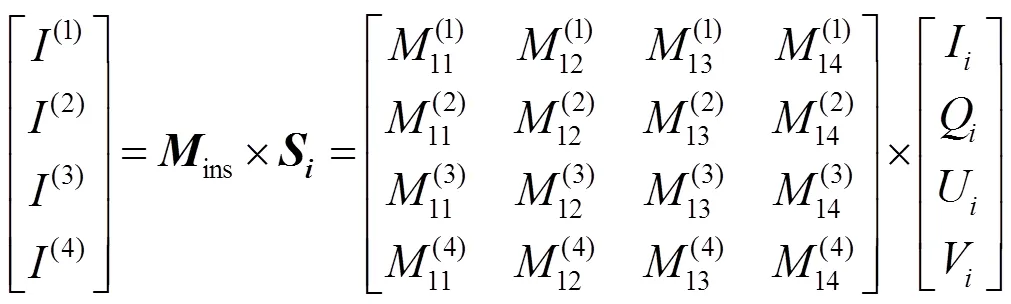
式中：ins為偏振成像系統的儀器矩陣。

若ins可逆，則可求得入射光的斯托克斯矢量i：

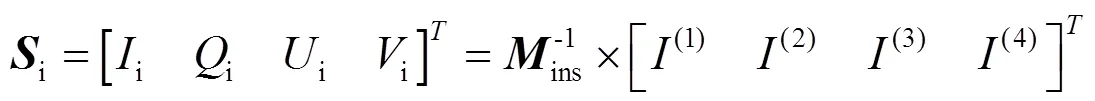
為滿足ins可逆條件，需要4個子通道的偏振分量互不相關，通常選擇0°、45°、90°和135°四個檢偏方向。對于理想偏振成像系統，對應的儀器矩陣為：

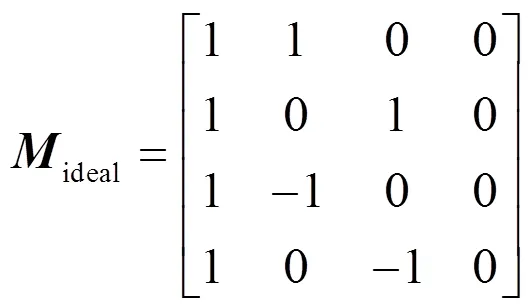
于是，依據斯托克斯矢量計算得到偏振度和偏振角：

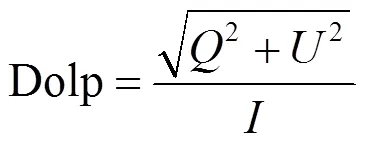
要得到動態目標場景的偏振信息，需要滿足：獲得同一時刻目標場景的4幅偏振度不同的圖像以及偏振成像系統的儀器矩陣。

1.2 SIP-DSWP同時偏振成像系統

偏振成像系統大致分為分時和同時成像兩類[9]。分時偏振成像裝置結構簡單、成本低，但偏振圖像在不同時間獲取，難以獲得動態目標場景的偏振信息。同時偏振成像在同一時刻獲得目標的四幅不同偏振態圖像，探測速度快，可用于快速變化目標的偏振探測。

結合分振幅和分孔徑同時偏振成像的特點[10]，我們設計了一套SIP-DSWP同時偏振成像系統[7]。如圖1，系統通過分振幅元件將入射光分為傳播方向垂直的兩路光（不調制光的偏振態）；然后通過分孔徑方式，將每一路光分為兩束偏振態正交的光沿一定夾角出射，分別成像在同一個探測器的左、右兩側，實現在兩個探測器上同時獲得不相關的4幅偏振分量圖像，實現動態場景的偏振成像；景物輻射在鏡頭3的焦平面成像，在鏡頭3的焦平面放置視場光闌，其后放置單色濾光片和鏡頭2，并與2個鏡頭1分別構成雙路中繼光學系統，將鏡頭2的像分別成像到探測器1和探測器2；在鏡頭2和鏡頭1之間依次放置消偏振分光棱鏡、1/2波片、渥拉斯頓棱鏡；鏡頭3的像經過鏡頭2和消偏振分光棱鏡分光，分為透射光路和反射光路，透射光依次經過快軸方位角為0°的1/2波片（平衡兩路光路的光程）、渥拉斯頓棱鏡和鏡頭1后，在探測器1的寬度方向形成左右兩幅圖像，分別對應0°和90°的偏振圖像；反射光經過快軸方位角為22.5°的1/2波片（相對于透射光路引入了45°的偏振方位變化）、渥拉斯頓棱鏡和鏡頭1后，由于反射時的鏡像效應，在探測器2上形成的左右兩幅圖像分別對應135°和45°的偏振圖像。當采用外觸發方式時，可同時在兩個探測器上獲得同一場景偏振方向相差45°的4種不同偏振態圖像。

SIP-DSWP同時偏振成像系統采集到的原始圖像如圖2，經過形態學處理、二值化處理、圖像邊緣提取、倒像/鏡像處理、分割配準等的配準圖像如圖3所示。

結合圖1和圖3可以看出：由于成像系統光路較長，加之光學元件難免的偏光性能差異，四路偏振光路不僅存在偏振特性差異（可采用儀器矩陣校正），而且在成像視場內也存在漸暈等不均勻成像，采用單一儀器矩陣描述全視場偏振成像性能存在困難。

2 SIP-DSWP同時偏振成像系統的分區儀器矩陣

2.1 分區儀器矩陣

根據E-P定標原理[11]，將偏振片放入積分球均勻的輸出端面與偏振成像系統之間的光路中，并在0°～350°范圍內每隔10°逐次產生線偏振均勻場景輻射，采集36組實驗設置下的偏振圖像提供系統儀器矩陣定標。注意到成像視場的非均勻性，將定標圖像分為3×3九個子區域（子區域大小170×216）)，通過對應子區域偏振圖像像素灰度的平均求取儀器矩陣，然后采用如圖4所示的加權系數對儀器矩陣進行加權平均，作為四通道SIP-DSWP同時偏振成像系統的儀器矩陣0。

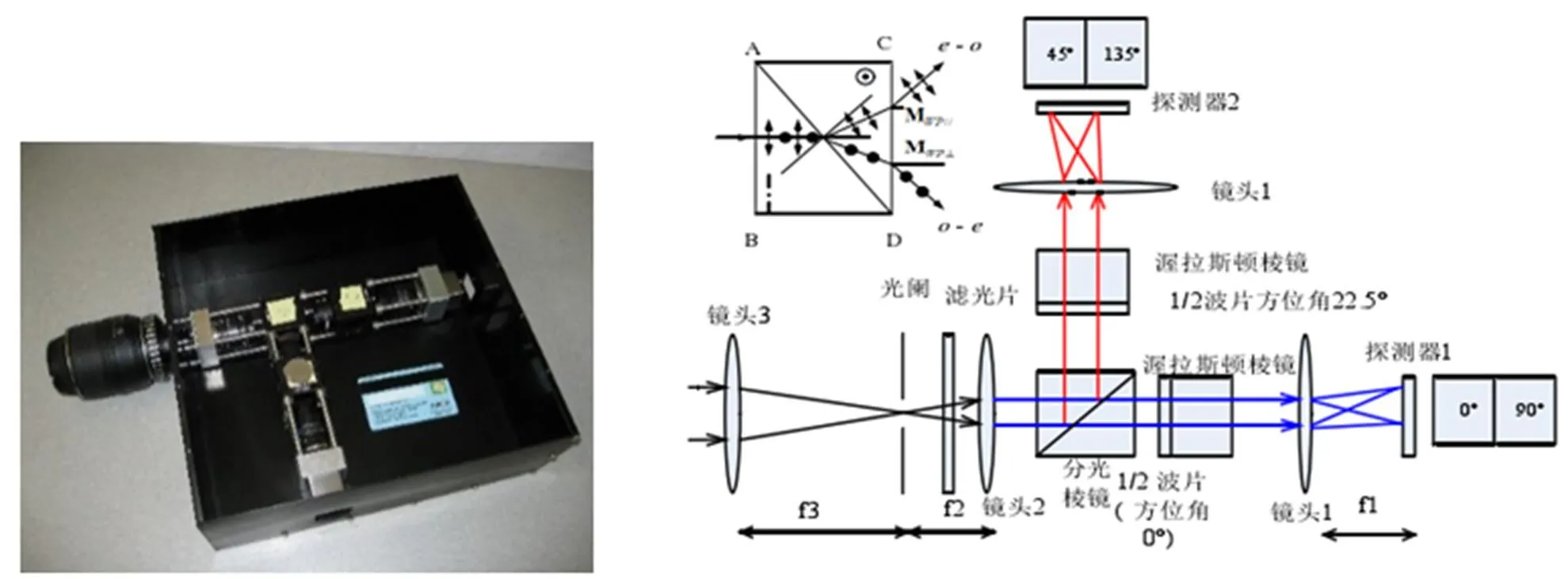
圖1 SIP-DSWP同時偏振成像系統及其成像原理圖

圖2 SIP-DSWP同時偏振成像系統獲取的原始圖像

圖3 SIP-DSWP同時偏振成像系統的配準圖像

如上所述，需要考慮漸暈等不均勻成像的影響，誠然，逐點建立儀器矩陣可獲得最佳的校正效果，但因逐個像素定標數據過大，會造成實際儀器矩陣參數儲存和校正計算量偏大，不利于實際實時的校正處理。為此，我們認為可采用分區儀器矩陣進行處理。這里直接采用圖4所示的9個子區域進行計算，得到的子區域儀器矩陣1至9如表1所示。可以看出：各個子區域的儀器矩陣存在差異，若僅用平均儀器矩陣0計算整幅圖像的斯托克斯矢量，不利于準確獲得景物的偏振信息。

2.2 對透明玻璃面傾角的非接觸測量實驗

如圖5，測量實驗是在陰天室外自然光照明條件下進行，將K9平板玻璃（＝1.5163）與SIP-DSWP系統水平放置在同一直線上（間隔2m），系統物鏡焦距為35mm，將平板玻璃的傾斜角度與偏振成像系統光軸分別調整成10°、20°、30°、40°、50°、60°、70°和80°共8個角度，并同時采集相應的0°、45°、90°、135°四幅玻璃平板的偏振圖像。

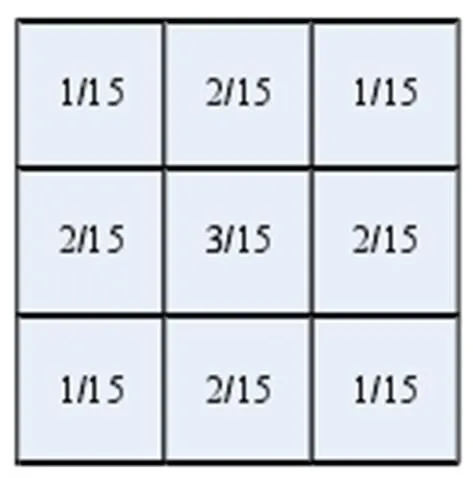
圖4 儀器矩陣加權系數

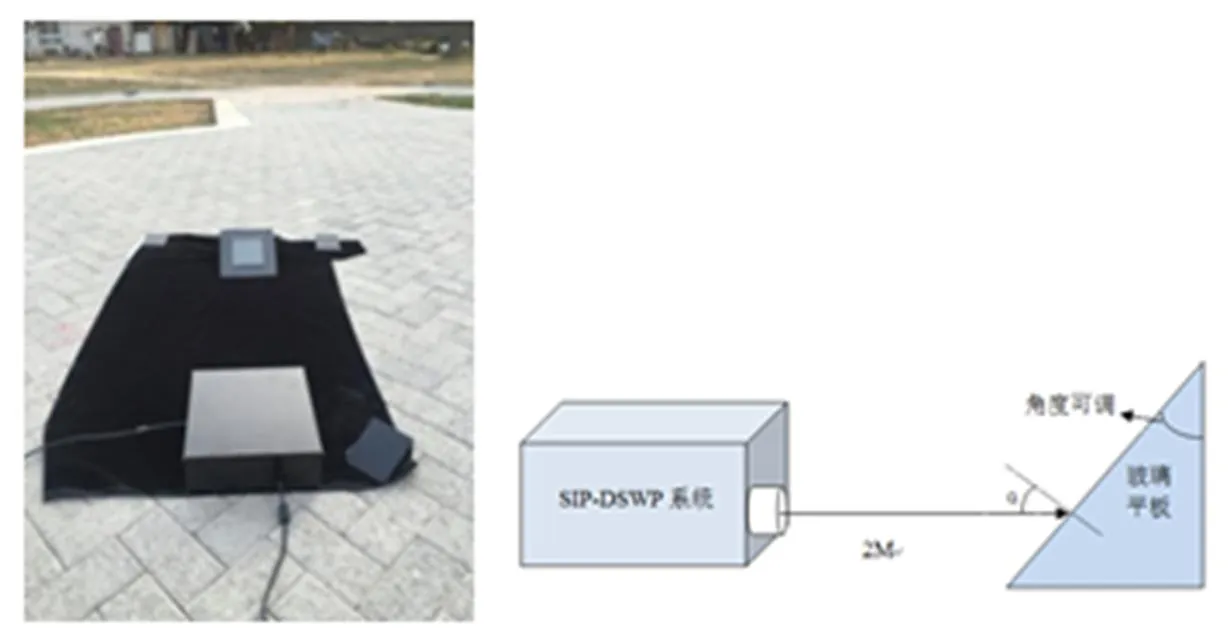
圖5 室外偏振成像系統玻璃平板角度檢測實驗

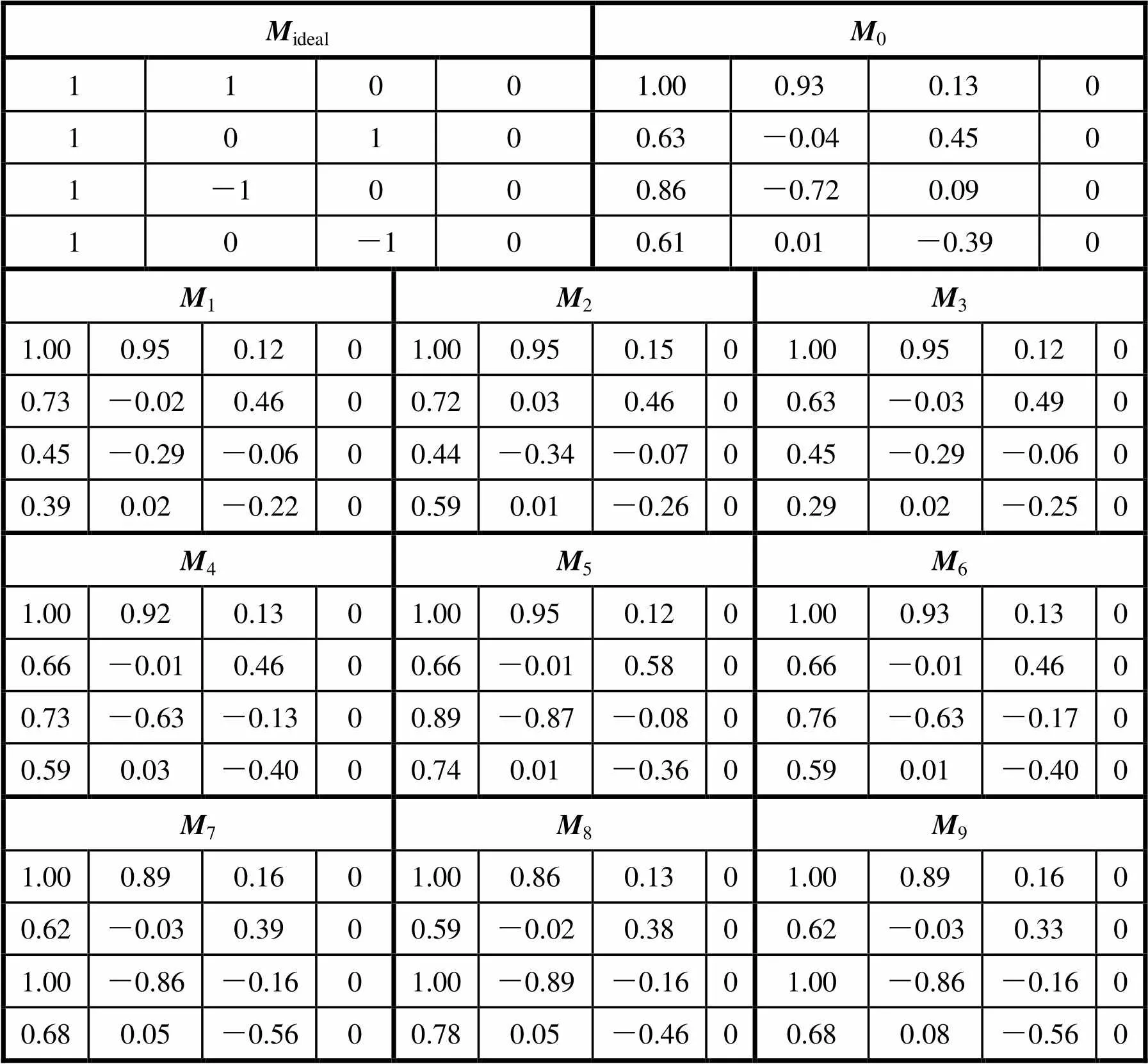
表1 理想、分區加權平均以及分區儀器矩陣

將采集到8組不同角度的圖像分為9個子區域并選取其中心點作為采樣點，分別用平均儀器矩陣與該子區域儀器矩陣計算斯托克斯矢量（由于80°玻璃平板無法充滿整個視場，特截取對應區域內玻璃板區域中心作為采樣點），進而按式(5)計算對應采樣點的偏振度、偏振角和玻璃平板傾角。

2.2.1 偏振度

表2給出分別采用平均和分區儀器矩陣計算的透明玻璃板偏振度。可以看出：1）用平均儀器矩陣重構的偏振度在分區5的結果與理想偏振度最為接近；2）用平均儀器矩陣在各分區計算的偏振度均優于采用平均儀器矩陣的結果；3）利用分區儀器矩陣計算的偏振度基本在分區5最接近理想偏振度。這說明由于圖像邊緣非均勻性，采用分區儀器矩陣是必要的，可減小偏振度的計算誤差。

2.2.2 偏振角

表3給出分別采用平均和分區儀器矩陣計算的玻璃板偏振角。同樣，用平均儀器矩陣重構的偏振角與理想偏振角基本在分區5最為接近；用分區儀器矩陣在各分區計算的偏振角均優于采用平均儀器矩陣的結果；分區儀器矩陣計算的偏振角最接近理想偏振角的分區較偏振度的離散更大，但基本在分區3、4和5，同樣說明分區儀器矩陣是必要的。

2.2.3 入射角

當入射光為自然光時，菲涅爾公式給出反射光偏振度Dolp與入射角、折射角l之間的定量關系[12]：

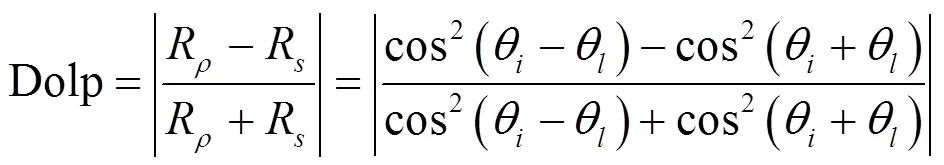
式中：為介質折射率。入射角與折射角之間滿足折射定律：sin＝×sin。

由圖5可知，光線入射角與玻璃平板的傾角一致。因此，根據SIP-DSWP系統確定的偏振度Dolp，可以進一步確定入射光的入射角即玻璃平板的傾角如表4所示。可以看出：①由平均儀器矩陣計算的入射角相對理想入射角有大有小，而由分區儀器矩陣計算的入射角均大于理想入射角，且偏差幅度均小于平均儀器矩陣；②平均儀器矩陣計算的最佳值均在第5區，分區儀器矩陣在第5區最接近理想數值。

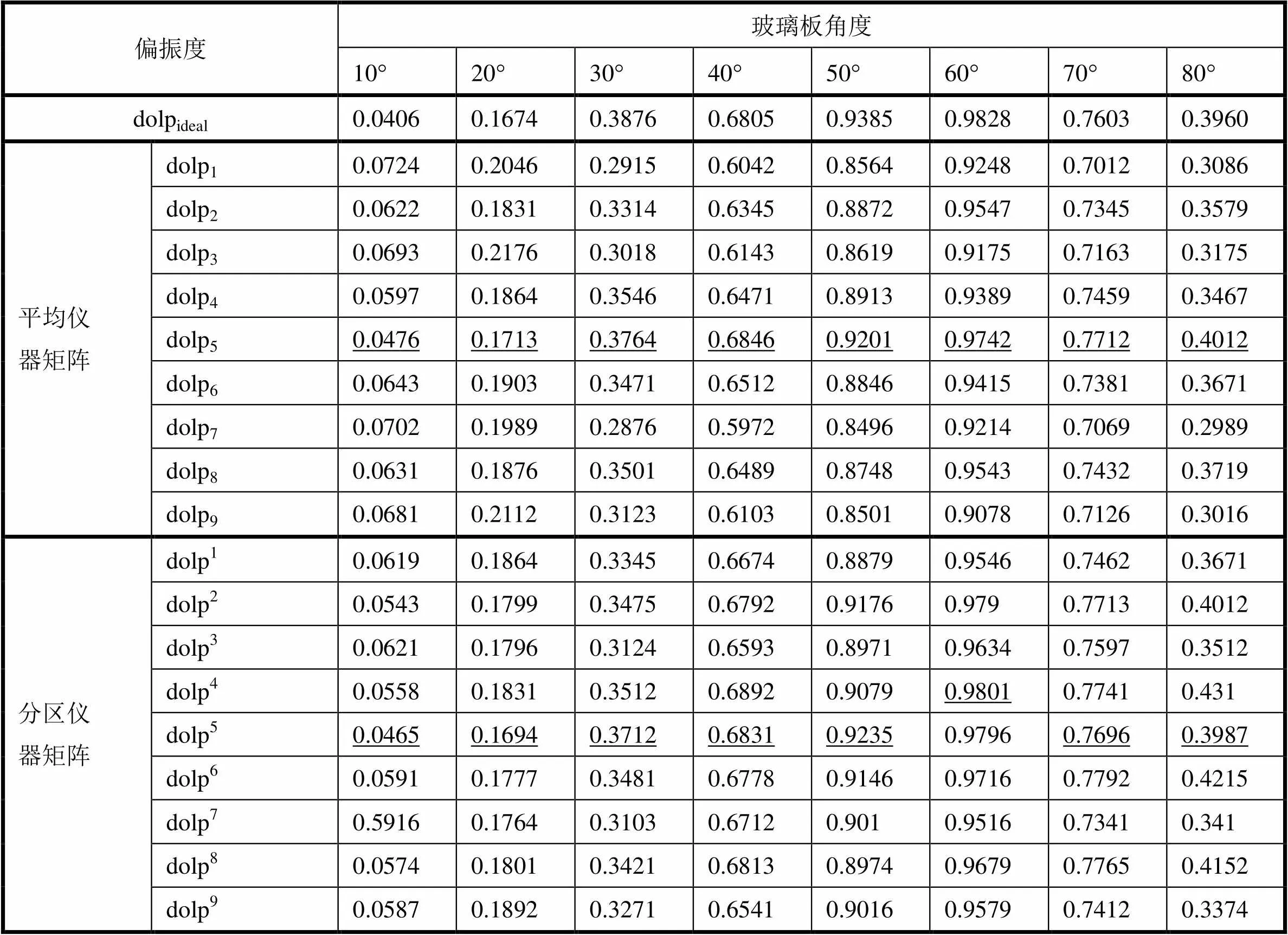
表2 平均儀器矩陣與分區儀器矩陣分別計算采樣點的偏振度

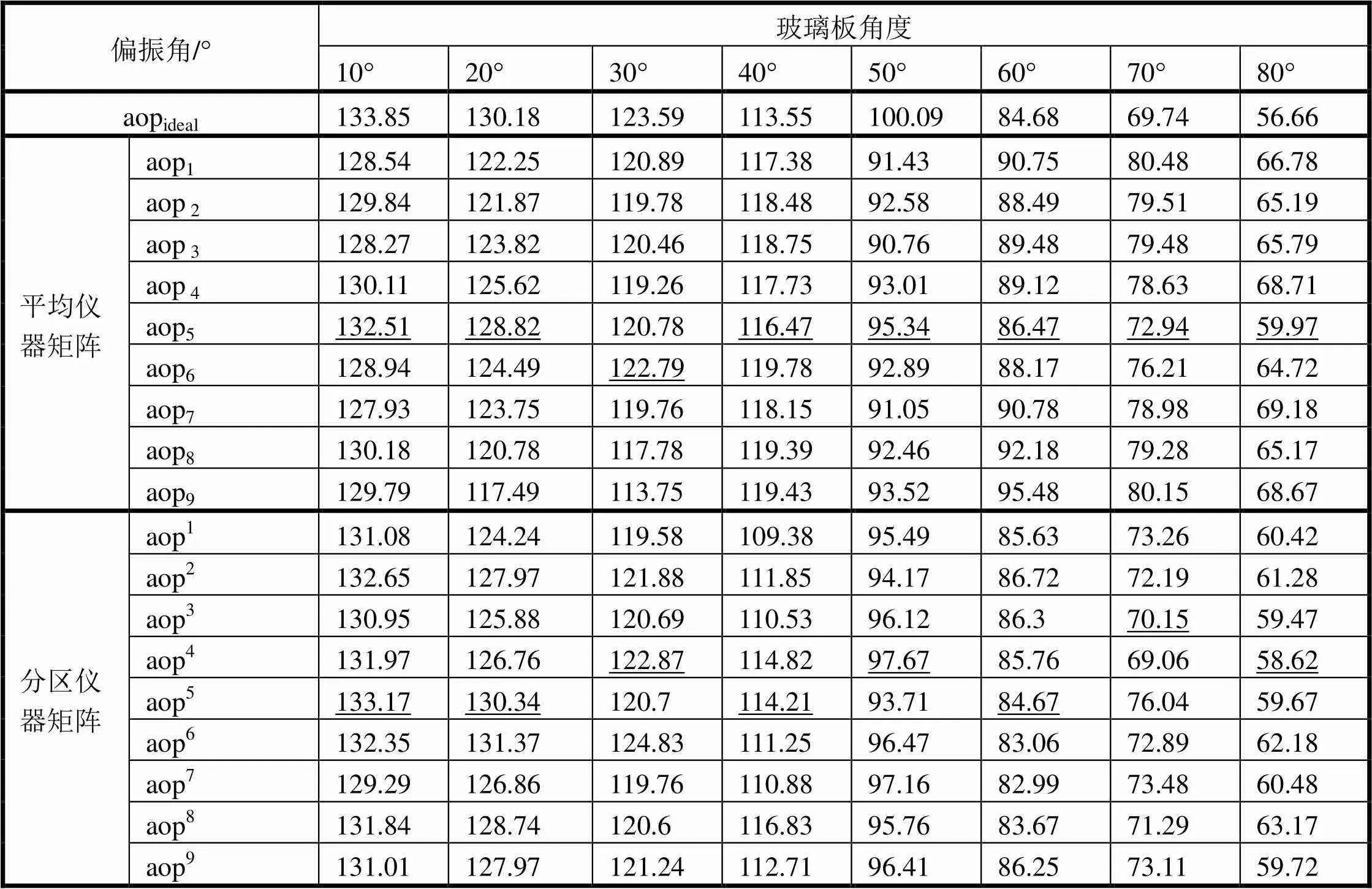
表3 平均儀器矩陣與分區儀器矩陣分別計算的采樣點偏振角

實際上，第5區屬于視場中心，其偏轉度、偏振角計算結果更為接近理想結果。對偏振成像的非理想性及軸外偏振信息及玻面傾角重構模型等，都是提高偏振信息及玻璃板的檢測精度需要進一步研究的內容。

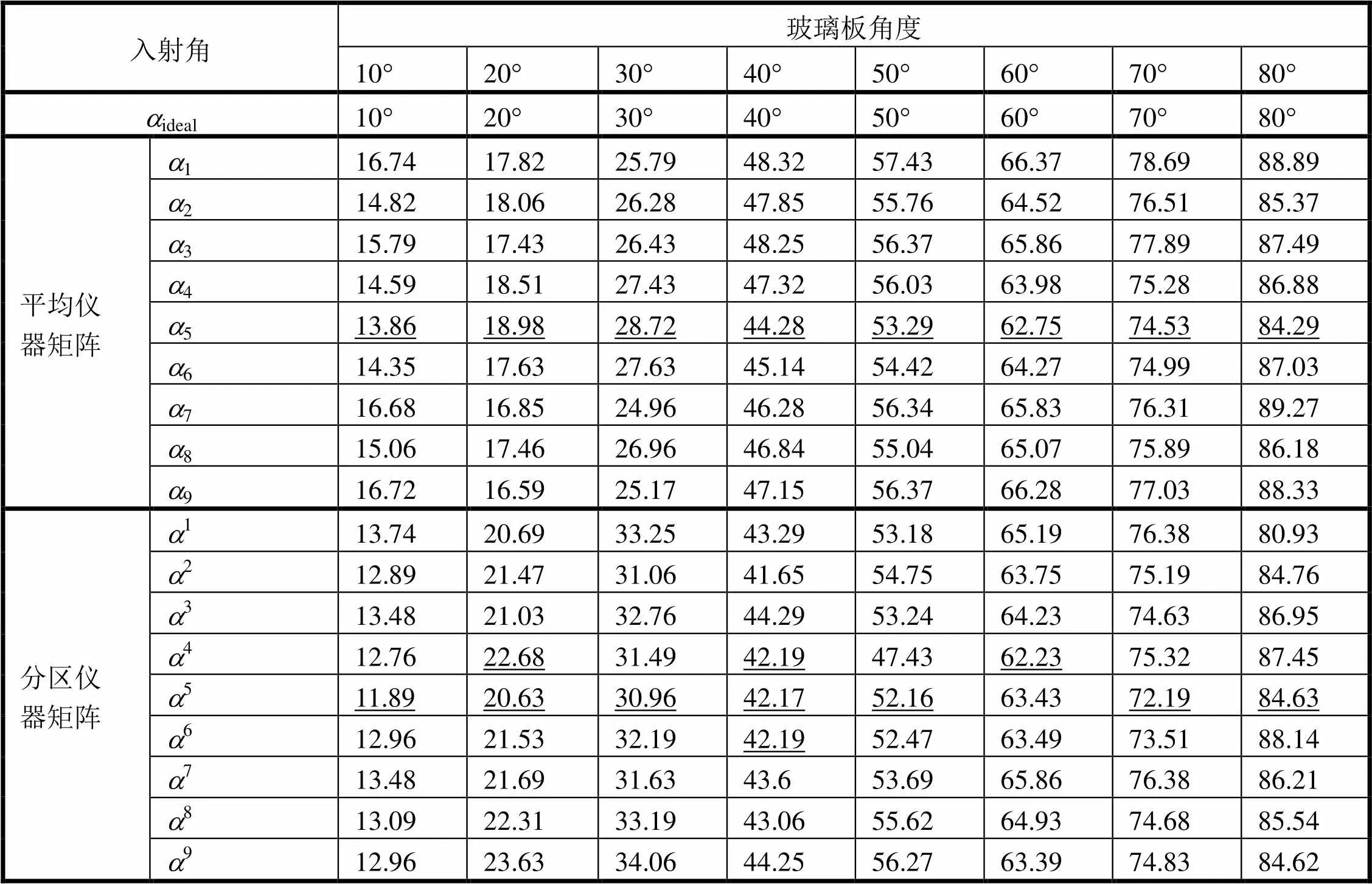
表4 平均儀器矩陣與分區儀器矩陣分別計算的采樣點入射角

3 總結

基于SIP-DSWP同時偏振成像系統，研究了在偏振成像系統視場邊緣存在漸暈條件下的分區儀器矩陣校正方法，利用E-P定標法將成像視場分為3×3個分區域進行分區域儀器矩陣標定，并對玻璃平板傾角進行了檢測實驗驗證，證明能夠獲得較文獻[6]采用9個子區域的平均儀器矩陣更準確的偏振度、偏振角和玻璃平板傾角信息，為后續偏振成像方法研究和定量檢測應用奠定理論基礎。

同時偏振成像系統能夠獲得動態場景目標的偏振信息，提高復雜背景下目標檢測率。我們以透明玻璃平板作為檢測目標，已驗證偏振成像可實現對水面波紋等的成像檢測，對發展新型水下目標探測技術具有意義。

[1] 劉敬, 金偉其, 王霞, 等. 透明物體面形偏振成像測量技術綜述[J]. 紅外技術, 2014, 36(9): 681-687.

Liu Jing, Jin Weiqi, Wang Xia, et al. Review of shape from polarization for transparent object[J]., 2014, 36(9): 681-687.

[2] 劉敬, 夏潤秋, 金偉其, 等. 基于斯托克斯矢量的偏振成像儀器及其進展[J]. 光學技術, 2013, 39(1): 56-65.

Liu Jing, Xia Runqiu, Jin Weiqi, et al. Review of imaging polarimetry based on stokes vector[J]., 2013, 39(1): 56-65.

[3] Zappa C J, Banner M L, Schultz H, et al. Retrieval of short ocean wave slope using polarimetric imaging[J]., 2008, 19(5): 120-125.

[4] Pezzaniti J.L., Chenault D., et al. Wave slope measurement using imaging polarimetry[C]//, 2009, 7317: 73170B-13.

[5] Schultz H, Corrada-Emmanuel A. System and method for imaging through an irregular water surface: US, US7630077[P]. 2009.

[6] 劉敬, 金偉其, 王霞, 等. 考慮探測器特性的光電偏振成像系統偏振信息重構方法[J]. 物理學報, 2016, 65(9): 094201-1.

LIU Jing, JIN Weiqi, WANG Xia, et al. Considering the probe gamma the polarization information reconstruction method[J]., 2016, 65(9): 094201-1.

[7] 劉敬, 金偉其, 王霞, 等. 雙分離渥拉斯頓棱鏡同時偏振成像系統設計[J]. 光學學報, 2015, 35(5): 0511001-10.

Liu Jing，Jin Weiqi，Wang Xia，et al. Design of Simultaneous Imaging Polarimetry with double separate Wollaston prism[J]., 2015, 35(5): 0511001-10.

[8] 廖延彪. 偏振光學[M]. 北京: 科學出版社, 2003.

Liao Yanbiao.[M]. Beijing: Science Press, 2003.

[9] R. M. Matchko. High-speed imaging chopper polarimetry[J]., 2008, 47(1): 16-18.

[10] J.S.Tyo. Review of passive imaging polarimetry for remote sensing[J]., 2006, 45(22): 5453-5469.

[11] Azzam. Arrangement of four photo-detectors for measuring the state of polarization of light[J]., 1985, 10(7): 309-311.

[12] L.B. Wolff. Polarization vision: a new sensory approach to image understanding[J]., 1997, 15(2): 81-93.

Partition Calibration Polarization Measurement Method of the Transparent Glass Surface Angle Based on SIP-DSWP System

WEN Renjie，LU Xiaotian，JIN Weiqi，LIU Jing，WANG Xia，GUO Hong

(,,100081,)

Because of the vignette effect of the edge field viewing, deflection exists in the reconstruction of polarization information using polarization imaging system. Therefore, in this paper, we proposed an imaging system correction method. The method was realized by filed viewing effect correction using the partition instrument matrix. The non-contact testing experiment of the glass-plate angle was conducted by calibrating the 3×3 partition instrument matrix of the SIP-DSWP synchronous polarization imaging system. The result of the experiment shows that the imaging edge field viewing effect and its noise are likely to affect the reconstruction of polarization imaging and polarization information. Compared to the instrument matrix, the partition instrument matrix can reconstruct the polarization information of the target view more accurately, increasing the test accuracy of the transparent glass-plate angle and subsequently establishing an academic foundation for the study of polarization imaging and quantitative testing application.

polarization imaging system at the same time，the stokes vector，polarization information，partitioning instrument matrix

O436

A

1001-8891(2017)09-0807-07

2016-12-05；

2017-06-29.

溫仁杰（1990-），男，碩士研究生，主要從事偏振成像及其圖像處理方面的研究。E-mail：635225289@qq.com。

金偉其（1961-），男，教授，博士生導師，主要從事光電圖像處理、夜視與紅外技術、光電檢測與儀器等方面的研究。E-mail：jinwq@bit.edu.cn。

國家自然科學基金面上項目（61575023），總裝預研基金。