沖積河流平灘面積調整模擬計算方法研究

于新榮陶西勇李凌云

（1.慈利縣零溪鎮水利管理站張家界市427200；2.慈利縣巖泊渡鎮水利管理站張家界市427200；3.長江科學院河流研究所武漢市430010）

沖積河流平灘面積調整模擬計算方法研究

于新榮1陶西勇2李凌云3

（1.慈利縣零溪鎮水利管理站張家界市427200；2.慈利縣巖泊渡鎮水利管理站張家界市427200；3.長江科學院河流研究所武漢市430010）

沖積河流水位達到新生河漫灘時的過流斷面面積稱為平灘面積，平灘面積調整對河道防洪、航運、水資源利用等多方面存在重要影響。文章基于河道沖淤變形基本方程和不平衡輸沙方程，推導建立了沖積河流河道平灘面積調整變化模擬計算方法。方法從理論上闡明了沖積河流平灘面積隨水沙條件變化的調整機理，揭示了不平衡輸沙是沖積河流河道斷面調整的根本原因。利用黃河下游高村站1960～2002年實測水沙資料對模擬計算方法進行了檢驗，結果表明所提出的方法能夠較好模擬出河道平灘面積的調整過程。研究成果有利于準確把握沖積河流斷面調整規律，可為相關河道治理與開發提供技術支持。

沖積河流平灘面積水沙條件不平衡輸沙

平灘面積是指水位達到新生河漫灘時的過水斷面面積，是研究河床演變的重要參數，也是河道主槽修復的重要指標。前人圍繞實際地形條件下平灘面積的確定、平灘面積的作用以及平灘面積與各種河流參數之間的定量關系等問題進行了大量研究，為認識河道主槽斷面的調整規律，以及開展河道整治和修復河道的輸水輸沙功能提供了基礎。然而由于河床演變本身是一個很復雜的過程，以往大量的研究成果也以經驗性的總結為主，缺乏理論基礎，計算方法物理意義不明確，給人們深入認識水沙條件變化與河道主槽調整之間的內在聯系帶來了很大的困難。本文從河床沖淤變形基本方程和不平衡輸沙方程出發，建立沖積河流的平灘面積計算方法，為從理論上闡明平灘面積的調整機理提供了基礎。

1 基本模型

對于沖積河流，河床變形通過挾沙水流的沖淤來實現。當河流沒有水沙量側向匯入時，一維河床沖淤變形的連續方程如下[1]：

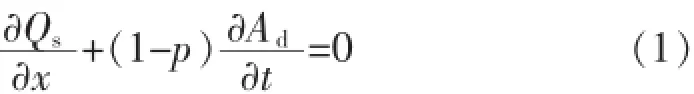
式中Qs——輸沙率；

Ad（Ad〉0河道淤積，Ad〈0河道沖刷）——沖淤面積；

p——淤積物空隙率；

x——沿程水平距離；

t——時間。

通常河道平灘面積Ab的調整體現在河道沖淤面積Ad的變化，在不漫灘的情況下，二者有如下關系：

式（2）代入式（1）可得：

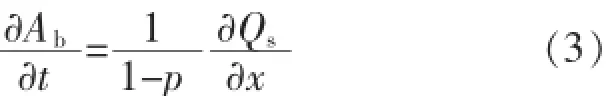
式（3）右端項展開：

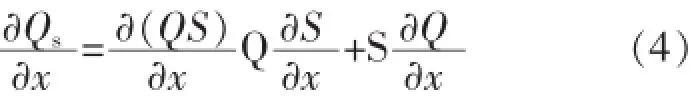
式中

Q——流量；

S——斷面平均含沙量。

假定來水來沙條件不變，則沿程流量不變，因此式（4）右端最后一項中?Q/?x為零。為計算方便，暫假設河道床沙為均勻沙，根據韓其為的不平衡輸沙方程，均勻沙條件下不平衡輸沙時平均含沙量沿程變化基本方程如下[2]：

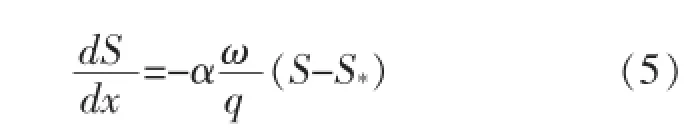
式中

S*——水流挾沙力；

α——含沙量沿程恢復飽和系數；

ω——泥沙顆粒在水中的沉速；

q——單寬流量。

式（5）改寫為偏導形式，并與式（4）一起代入式（3）可得：

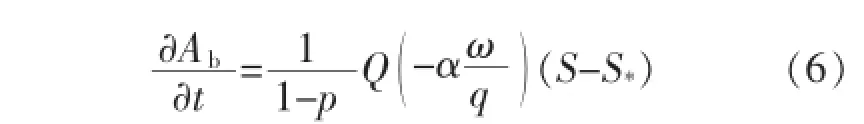
式（6）僅涉及對時間的求導，可將偏導數直接改寫為全導數的形式。假設水面寬為B，化簡可得：

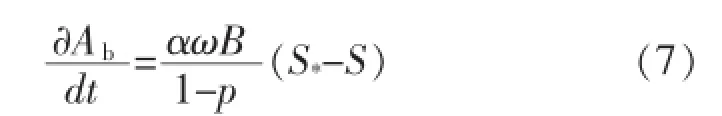
式（7）即為河道平灘面積調整的基本方程。從中可以看出，平灘面積調整的根本原因是河道不平衡輸沙，即來水含沙量與水流挾沙力不相等，河道平灘面積的調整通過河道沖淤變形來實現。式（7）揭示了來水來沙條件與平灘面積調整之間的相互作用過程。

2 實用模型

式（7）給出了平灘面積調整的基本方程，但方程中包含有水流挾沙力S*項，基于兩方面的原因需要對S*項進行處理：一是常見的水流挾沙力公式使用不方便。常用的挾沙力公式一般涉及到流速、沉速或者粒徑等，但這方面的資料往往比較缺乏；二是水流挾沙力的概念一般基于較短的時間尺度而言，一般為幾天幾個小時甚至幾分幾秒，關注的是較短時間內水流的挾沙能力，體現短時間內的河道主槽的沖淤情況，而這里我們考慮的是河道主槽在一定水沙條件下長時間作用后的調整情況，關注的時間尺度一般為幾個月或者一年甚至更長時間。基于以上原因，下面對式（7）的計算進行變換。

當給定了上游來水來沙條件時，河道會通過沖淤的形式進行調整，調整的結果是使河道含沙量S向水流挾沙力S*靠近，最終河道平灘面積由Ab調整至Ae時達到平衡狀態，此時含沙量S與水流挾沙力S*相等。因此可以將S*看成是Ae對應的某種特性，而S看成是Ab對應的某種特性。為方便計算做如下假定：

式中k、k*為系數，式（8）代入式（7）得：

采用近似k=k，*其值大小與水面寬、含沙量恢復飽和系數以及空隙率等因素有關，實際計算過程中可根據實測資料率定。代入式（9）簡化為：

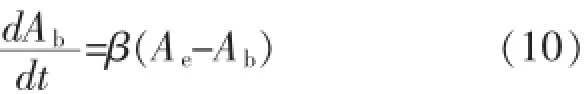
可以看到，式（10）與吳保生所建立的平灘面積滯后響應模型具有相同的形式[3]。不同的是平灘面積滯后響應模型是基于沖積河流具有自動調整的原理，其調整速率與當前狀態同平衡狀態之間差值成正比的假設得出，而本文是基于河床沖淤變形基本方程和不平衡輸沙方程推導得到，其理論基礎相對較強，這也正是以往常用的計算方法所缺乏的。

當來水來沙條件確定時，平灘面積平衡值Ae即為一定值。因此式（10）有以下形式的通解（負指數衰減函數）：

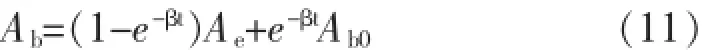
其中Ab0為t=0時的平灘面積。吳保生的研究表明，平灘面積的調整與來水來沙條件密切相關，平灘面積平衡值Ae可采用如下方程計算[4]：

式中

Qf——汛期平均流量；

ξf——汛期平均來沙系數，其值為汛期平均含沙量與汛期平均流量之比。

k、b和c——待定系數和指數，根據實測資料率定。

將式（12）代入式（11）得：

式（13）即為實用的平灘面積計算模型。

3 模型應用

黃河下游是典型沖積河段，其河道斷面形態隨水沙條件頻繁劇烈變化。本文收集了黃河下游高村水文站1960～2002年系列水沙及平灘面積資料，根據這些水沙資料，率定式（13）中的相關參數，可得k=6.6，b=0.171，c=－1.075，β=0.213，代入式（13）得：

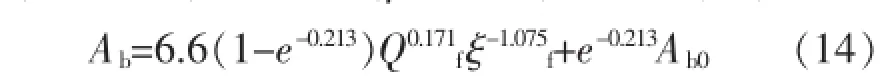
式（14）計算結果如附圖所示。計算值與實測值符合很好，相關系數R2=0.90。從附圖可以看出，利用該方法模擬計算高村站的平灘面積，計算值與實測值歷年變化過程基本一致，說明該方法能夠真實反映平灘面積隨水沙條件的調整規律。

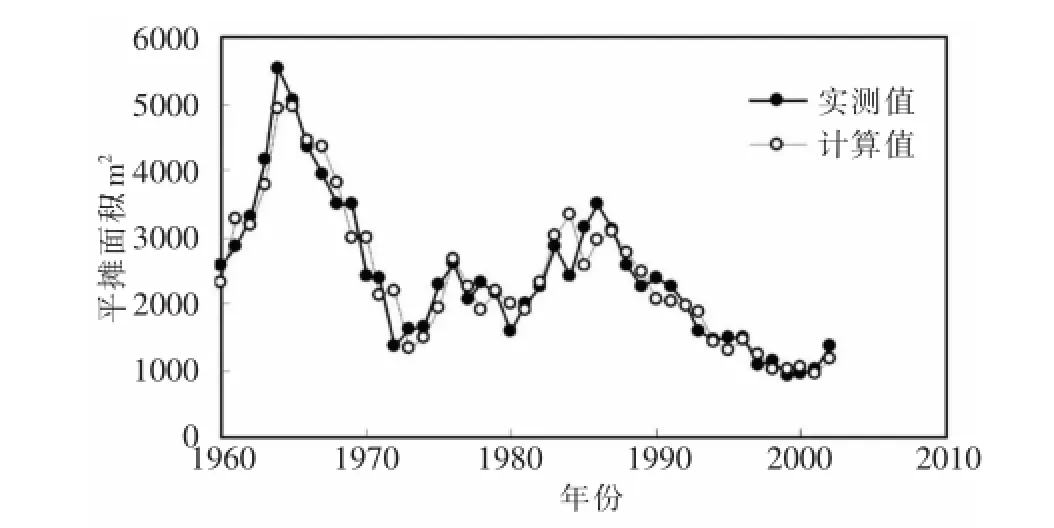
附圖式（14）計算高村站平灘面積與實測值對比

同時我們也看到，有些年份計算值與實測值變化趨勢不一致的情況，分析原因是原模型是基于不漫灘的情況下推導得出。當洪水不漫灘時，河道若發生淤積，則淤積全部集中在主槽，主槽斷面減小，式（2）即反映了這種情況；當洪水出現漫灘時，河道發生淤積，其中部分淤積量將分布在灘地，這部分淤積量不僅不會使主槽斷面面積減小，反而有可能因抬高了灘唇高程使主槽斷面面積擴大，這與式（2）反映的情況不一致。因此下一步的研究可在考慮漫灘的情況下對模型進行改進。

4 結論

本文從河道沖淤變形基本方程和不平衡輸沙方程，推導出了平灘面積調整模擬計算方法，并利用黃河下游高村站水文站1960～2002年的水沙實測資料進行了驗證。主要結論如下：

（1）推導建立了具有一定理論基礎的平灘面積計算方法式（13），方法反映了來水來沙條件同河道平灘面積調整之間的內在聯系。

（2）利用黃河下游高村水文站1960～2002年實測水沙資料驗證表明，式（13）能夠很好地描述河道平灘面積的調整規律。

[1]錢寧，張仁，周志德.河床演變學[M].北京：科學出版社，1987.

[2]韓其為.水庫淤積[M].北京：科學出版社，2003.

[3]Wu B S,Xia J Q,Fu X D,et al.Effect of altered flow regime on bankfull area of the Lower Yellow River,China[J].Earth Surface Processes and Landforms,2008,33（10）：1585－1601.

[4]吳保生.沖積河流平灘流量的滯后響應模型[J].水利學報，2008，39（6）：680－687.

2016－07－20）

于新榮（1980－），女，湖南慈利人，大學本科，工程師，現在慈利縣零溪鎮水利管理站工作，聯系電話：0744－3223633；陶西勇（1976－），男，湖南慈利人，大學本科，工程師，現在慈利縣巖泊渡鎮水利管理站工作，聯系電話：0744－3510006；李凌云（1982－），男，湖南慈利人，博士，高級工程師，主要從事水力學及河流動力學相關研究工作，聯系電話：027－82926172。