基于MATLAB的超磁致伸縮致動器動態模型研究

陽學進

（武漢輕工大學，湖北武漢430020）

基于MATLAB的超磁致伸縮致動器動態模型研究

陽學進

（武漢輕工大學，湖北武漢430020）

超磁致伸縮致動器具有響應快，應變大的特點，廣泛應用于各種精密場合。而超磁致伸縮致動器的輸出與輸入的模型研究，是其應用到實際中的基礎。在忽略了電渦流以及線圈電感系數變化的影響下，建立了超磁致伸縮致動器的動態模型，并在MATLAB中進行了動態仿真，驗證了模型的正確性。

GMA；MATLAB；動態模型

超磁致伸縮材料（Giant Magnetostrictive Material簡稱GMM，是一種能夠實現電磁能與機械能相互轉化的材料[1]，其具有高的應變值，高能量轉化率，快響應速度，被應用在超聲換能器、測量與傳感、控制驅動等領域[2]。本文以超磁致伸縮材料的Joule效應為理論基礎，分析了以GMM制成的超磁致伸縮致動器（Giant Magnetostrictive Actuator簡稱GMA，的輸入輸出關系模型，并在MATLAB中進行了模型仿真。

1 超磁致伸縮致動器（GMA）的結構

GMA的設計主要需要處理以下幾個方面的問題[3]：GMA中磁路設計，電流的確定，驅動器機構設計，線圈冷卻處理。其基本設計過程為：GMM棒尺寸的設計與選擇，閉合磁路的設計、GMM所處的磁場設計、預壓機構設計、冷卻系統設計[4]。

所設計出的GMA的結構參數如下表1所列。

表1 GMA主要參數表

2 超磁致伸縮致動器的動態模型

將GMA進行簡化，得到的力學模型如圖1所示。GMM制成的棒至于線圈內部。當線圈通過電流時，GMA會在末端輸出微小位移，其對負載產生輸出力fGMM.

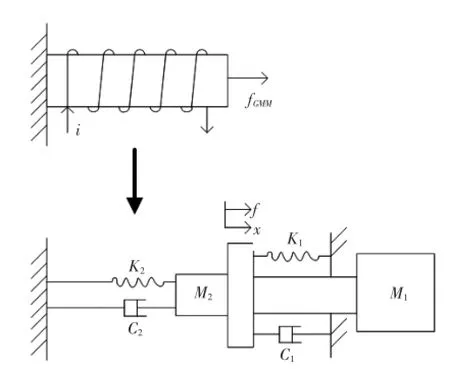
圖1 GMA動態模型

取位移x作為自變量，系統的微分方程為：

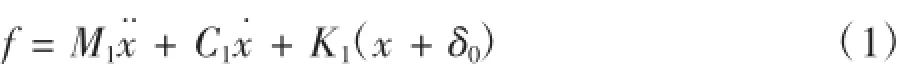
式中，δ0為預壓彈簧的初始伸縮量；K1為預壓彈簧的剛度系數；C1為輸出軸與彈簧組成的整體的阻尼系數；M1為輸出軸及負載的質量。

得到GMM棒的輸出力大小為

對于GMM棒，考慮其質量和阻尼的影響，可以得到其運動微分方程：

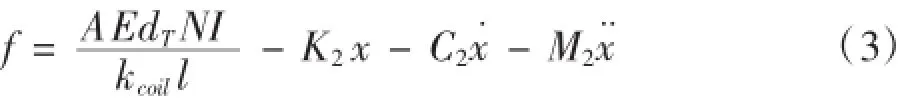
K2、C2、M2分別為GMM棒的等效剛度系數、阻尼系數、質量。將其位移函數表示為形狀函數與廣義坐標乘積的形式，可求出M2、K2、C2[3]。

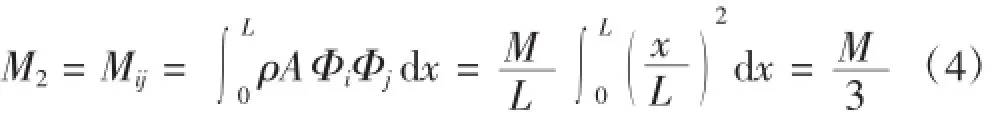
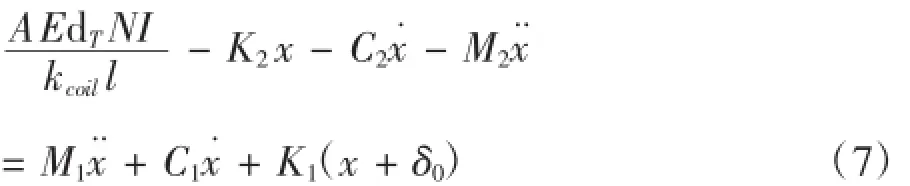
則GMA的系統微分方程變換為：對上式進行拉普拉斯變換，得到系統的傳遞函數為：

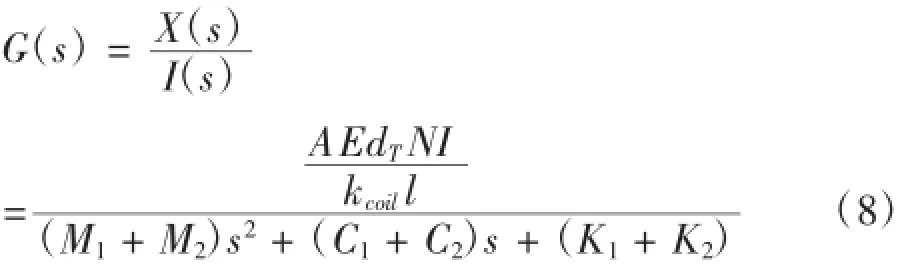
將參數代入到公式（4）可以得到系統的傳遞函數為：

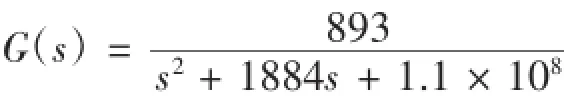
3 MATLAB仿真

針對上述得到的超磁致伸縮致動器的傳遞函數，借助階躍相應函數進行響應分析，進行系統性能分析，其響應如圖2所示。從其中可以看出，系統的響應時間為4 ms，具有較好的響應性能。

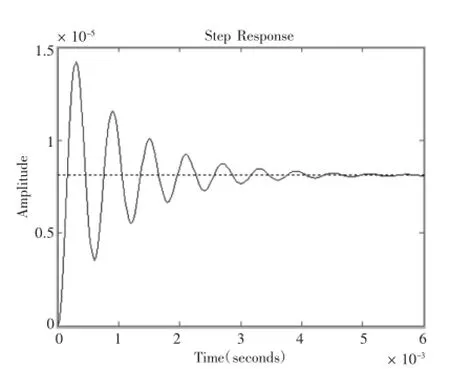
圖2 系統階躍響應圖

4 結束語

本文對所涉及的GMA進行模型提煉，得到了忽略了電渦流以及線圈電感系數變化的影響下的系統動態模型，并得到了系統的傳遞函數。最后通過MATLAB進行仿真分析，驗證了系統的良好響應性能。

[1]姜德生.智能材料器件結構域應用[M].武漢：武漢工業大學出版社，2000.

[2]盧全國，陳定方.GMM的發展現狀及其在精密致動器件中的應用[J].湖北工業大學學報，2006，21（3）：92-94.

[3]Goran Engdahl.Handbook of Giant Magnetostrictive Materi als.Sa Diego：Academic Press，2000.

[4]陽學進.考慮磁滯瞬態損耗的GMA在振動主動控制中的應用[D].武漢：武漢理工大學，2014.

Research on Dynamic Model of GMA Based on MATLAB

YANG Xue-jin
（Wuhan Polytechnic University，Wuhan Hubei 430020，China）

GMA is widely used in various precision occasions with fast response，large strain.The relationship of the output and input for GMA is the basis for its application in practice.So the dynamic model of the giant magnetostrictive actuator is established under the influence of eddy current and inductance of the coil.The dynamic simulation is carried out in MATLAB，which verifies the correctness of the model.

GMA；MATLAB；dynamic model

TP216

：A

：1672-545X（2017）01-0054-02

2016-10-07

陽學進（1989-），男，湖北監利有，碩士，助教，研究方向：智能結構與器件。