高等數學中不等式證明的幾類常用方法

潘娟娟，凌雪岷

（安徽新華學院 通識教育部，安徽 合肥 230088）

高等數學中不等式證明的幾類常用方法

潘娟娟，凌雪岷

（安徽新華學院 通識教育部，安徽 合肥 230088）

不等式在高等數學中的應用非常廣泛，但是其本身邏輯性較強，證明方法多樣，學習難度較大.本文立足高等數學，通過實例補充介紹了6種比較常用的證明不等式的方法，對每種方法給出了具體的證明思路，并輔以典型例題，旨在使學生對不等式的證明有更深的理解和掌握.

高等數學；不等式；證明

不等式的證明是高等數學中重要的考察內容，正確的使用不等式可以將一些復雜的數學問題簡單化，但是不等式證明方法多樣且繁雜，學生在使用時往往無法選擇最合適且最簡便的方法，因此對不等式證明方法進行總結和歸納很有必要，既可以提高教師的教學水平，還可以增強學生學習的效果.基于不等式的重要性，本文總結了證明不等式的幾種常用的方法，并配以具體的例子，便于學生更好的掌握不等式證明的技巧，在以后的學習中可以熟練的選擇合適的簡潔的證明方法.

1 利用函數的性質證明不等式

1.1 函數的凹凸性

定義1[1]設f(x)在區間I上連續，如果對任意兩點x1,x2恒有

那么稱f(x)在I上的圖像是(向上)凹的(或凹弧)；

如果恒有

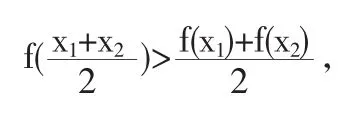
那么稱f(x)在I上的圖像是(向上)凸的(或凸弧).

說明 函數判定函數的凹凸性，一般我們不通過定義去判定，而是通過凹凸性的判定定理來判定，設f(x)在[a,b]上連續，在(a,b)內具有一階和二階導數，那么若在(a,b)內f"(x)＞0 (或f"(x)＜0)，則f(x)在[a,b]上圖形是凹(或凸)的[1].

1.2 函數的單調性

利用函數的單調性比較函數的大小，是高等數學不等式證明中常用到的方法之一.

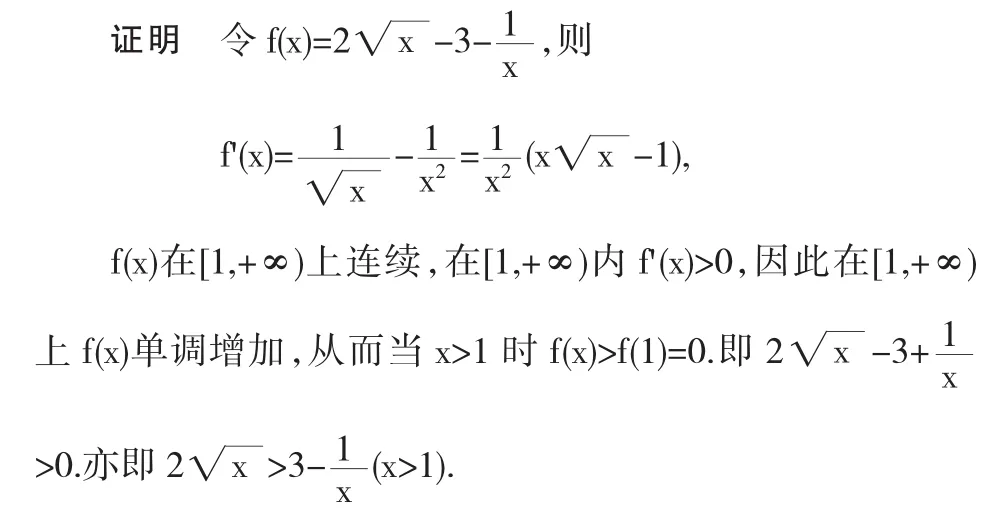
說明 利用函數單調性證明不等式的一般步驟:

(1)構造輔助函數f(x)；

(2)根據f'(x)的符號判定函數的單調性；

(3)根據函數f(x)的單調性，得出所求不等式.

2 利用Lagrange中值定理和Cauchy中值定理證明不等式

2.1 Lagrange中值定理[1]

如果函數f(x)滿足:

(1)在閉區間[a,b]上連續；

(2)在開區間(a,b)內可導，那么在(a,b)內至少有一點ξ (a＜ξ＜b),使等式

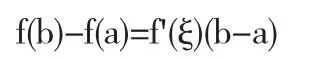
成立.

例3 設b＜a＜0，證明nan-1(b-a)＜bn-an＜nbn-1(b-a).

證 設f(x)=xn,顯然f(x)在區間[a,b]上滿足拉格朗日中值定理的條件，根據定理，應有f(b)-f(a)=f'(ξ)(b-a)(a＜ξ＜b)，由于f'(ξ)=nξn-1，因此上式可化簡為bn-an=nξn-1(b-a)，又由于a＜ξ＜b，有nan-1(b-a)＜nξn-1(b-a)＜nbn-1(b-a)，

即nan-1(b-a)＜bn-an＜nbn-1(b-a).

說明 利用Lagrange中值定理證明不等式的步驟如下:

(1)通過觀察不等式經過恒等變形可以化成函數值之差的形式，則可考慮運用拉格朗日中值定理，并合理設定f(x)；

(2)根據a＜ξ＜b對拉格朗日中值定理進行適當的放縮，推導出所證不等式.

2.2 Cauchy中值定理[1]

如果函數f(x)及F(x)滿足:

(1)在閉區間[a,b]上連續；

(2)在開區間(a,b)內可導；

(3)對任一x∈(a,b),F'(x)≠0,

那么在(a,b)內至少有一點ξ(a＜ξ＜b)使不等式

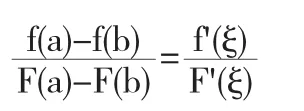
成立.

例4 設e＜a＜b＜e2.證明

3 利用Taylor公式證明不等式

高等數學中，泰勒公式除了用于逼近一些較復雜的的函數、近似值計算以及求函數極限以外，還可以用于證明一些幾何不等式.

例5 b＞a＞e證明:ab＞ba.

說明 運用泰勒展開具體步驟如下:

(1)合理給出輔助函數f(x)，給出函數在某點的泰勒展開式，展開式的階數根據具體題設來確定；

(2)根據所證不等式，對朗格朗日余項進行適當的放縮，從而證明出所給不等式.

4 利用函數的最值證明不等式

利用閉區間上連續函數的有界性與最大值最小值定理，求出函數f(x)在區間的最大值M和最小值m，則該函數在區間段內任意值都滿足f(x)≤M或者f(x)≥m.

5 利用定積分的性質證明不等式

5.1 定積分的估值定理[2]

設M及m分別是函數f(x)在區間[a,b]上的最大值和最小值，則

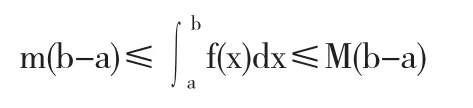
說明 找出被積函數的在積分區間上的最大值和最小值，可以估計積分值的大致范圍，從而證明了不等式.

5.2 積分中值定理[1]

如果函數f(x)在區間[a,b]上連續，至少存在一個點ξ，使下式成立:

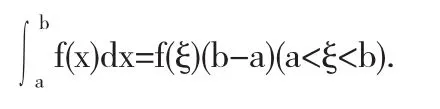
積分中值定理是解決含有積分不等式問題的重要方式之一.

例8 設f(x)在[0,1]連續單調減，

6 利用定積分中的一些著名不等式證明不等式

柯西-施瓦茨不等式

例9 設f(x)在區間[a,b]上連續，且f(x)＞0.證明:

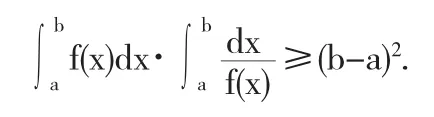
說明 利用琴生不等式證明不等式時，要選用合適的輔助函數，然后通過求一階二階導數得到函數的凹凸性，根據琴生不等式求證.

8 結語

本文僅僅總結歸納了高等數學中七種常用的證明不等式的方法，但是教學過程中并不僅僅局限于上述若干種方法，而且同一個問題也可以選擇不同的證明方法去解決，這就需要教師和數學愛好者在平時的教學工作中不斷去發覺和探索，從而可以綜合運用各種方法和技巧靈活解決不等式證明的相關問題.

〔1〕同濟大學數學系.高等數學[M].北京：高等教育出版社，2015.

〔2〕裴禮文.數學分析中的典型問題和方法[M].北京：高等教育出版社，2001.

O172

A

1673-260X（2017）02-0001-03

2016-09-02

安徽省高校省級重點項目（KJ2016A310）；安徽省級質量工程項目名師工作室(2014msgzs168)