一種新的基于NIG模型的四元數小波圖像去噪方法

朱 芳，劉 衛

?

一種新的基于NIG模型的四元數小波圖像去噪方法

朱 芳1，劉 衛2

（1. 安徽新華學院通識教育學院，安徽 合肥 230088；2. 中國科學院合肥智能機械研究所，安徽 合肥 230031）

基于正態逆高斯模型和快速雙邊濾波，本文在四元數小波變換域提出一種新的圖像去噪算法。首先將噪聲圖像進行四元數小波變換分解，其次應用快速雙邊濾波算法處理低頻子帶，高頻子帶采用正態逆高斯模型對其進行建模，并結合最大后驗概率估計準則推導出相應的閾值函數，最后結合最優線性插值得到的閾值算法實現圖像去噪。對提出的算法進行實驗仿真，通過與已有優秀去噪算法比較，結果顯示本文方法取得了不錯的視覺效果，且在峰值信噪比和平均結構相似性上都得到一定的提高。

四元數小波變換；雙邊濾波；正態逆高斯模型；最大后驗概率估計；最優線性插值；圖像去噪

0 引言

當今社會已經進入數字化的信息時代，超大容量、實時地、高效率地獲取各種有用信息已成為當代的典型特點。大量數據顯示，人類有70%以上的信息都是來源于圖像，自然圖像在獲取和傳輸過程中都會受到不同程度噪聲的污染，如何快速有效地去除噪聲已成為當今學者研究的重點。經典的去噪方法主要有空間域濾波和變換域濾波，都在一定程度上實現了噪聲去除，但在降噪和保留細節折中方面難以令人滿意。小波變換作為新型的時頻分析方法，具有多尺度、多分辨率、低熵性及去相關性等特點，其中Donoho基于小波變換提出一系列的閾值去噪方法[1-2]。由于小波變換不具有平移不變性，使得去噪后的圖像出現偽吉布斯現象，為此，1998年Kingsbury等提出雙樹復小波變換（DT-CWT）[3]并廣泛應用于圖像去噪中，DT-CWT達到近似平移不變性，同時方向特性也增強。Chang[4]等人利用廣義高斯模型建模原始圖像的小波系數，提出BayesShrink去噪算法。Portilla[5]等人則借助一種高斯尺度混合模型實現圖像去噪。2002年，Sendur[6]等基于小波系數尺度間關系提出Bishrink算法。這些方法一定程度上達到了圖像去噪的效果，但仍舊存在一些局限性。Cho D[7]在2005年基于Gaussian、GGD、Non-Gaussian提出了多元廣義高斯模型，但去噪過程中涉及到較為復雜的參數估計。2006年，Cunha[8]等人提出了非下采樣Contourlet變換，但NSCT計算復雜度較高，所需的運行時間較長，同時Guo[9]等人提出了Shearlet變換，但該方法不具備平移不變性，在圖像融合時容易在奇異點附近產生偽吉布斯現象。由于傳統的實小波變換缺乏平移不變性和方向選擇性，同時雙樹復小波變換（DT-CWT）具有近似平移不變性，但相位信息不夠豐富，在圖像信號局部特征表征時容易產生相位歧義，2008年，Chan[10]等提出了四元數小波變換（QWT），是基于二維Hilbert變換給出的一種新的多尺度分析工具，具有近似平移不變性和3個相位信息，克服了實小波與復小波的不足，且廣泛應用于圖像分割、邊緣檢測和圖像重構等。

常見的基于變換域的圖像去噪方法主要集中在處理變換后的系數上面，處理的原則一般都是選擇合適的統計模型來逼近分解后的系數，其中基于最大后驗概率（MAP）準則的Bayesian估計是經典的方法之一。一般情況下，變換域中分解系數的先驗概率密度函數中含有未知參數，其中Laplacian密度函數中只含有一個未知參數，是描述分解系數的標準模型，廣義Gaussian[11]密度函數中涉及兩個參數等，然而這些方法在方差不同的條件下不能準確建模分解后系數，因為它們忽略了系數層間和層內之間的關系。正態逆高斯模型（NIG）的密度函數中含有4個參數，其模型可以用來描述任意形狀的曲線，可以準確建模不同程度拖尾的圖像分解系數，因而用其作為QWT分解系數的先驗模型是合適的。2011年，賈建[12]等人運用正態逆高斯模型（NIG）[13]建模NSCT變換后的系數，在去噪效果上取得了一定成效。

本文提出一種基于快速雙邊濾波[14]和NIG模型的QWT變換域圖像去噪算法，充分考慮圖像經過QWT變換后低頻和高頻部分，因為圖像經過多尺度幾何變換后，噪聲主要集中在高頻子帶，但低頻子帶中仍舊含有一些噪聲。新算法將QWT變換與NIG模型結合，對變換后的低頻子帶采用快速雙邊濾波算法，高頻子帶的系數用NIG模型進性建模，并利用Bayesian最大后驗概率估計推導出閾值函數，最后結合最優線性插值閾值算法（OLI-shrink），實現圖像去噪的目的。實驗結果表明本文所提方法可以取得較好地去噪效果。

1 基于NIG模型的四元數小波變換（QWT）

1.1 四元數小波變換

W. R. Hamilton[15]在1843年基于復數理論提出四元數概念，也可作為特殊的Clifford代數。設四元數＝r＋i＋j＋kk且r、i、j、k?，r為四元數的實部，i、j、k為四元數的虛部，i、j、k為正交虛數單位且滿足下式：

四元數的共軛記為：*＝r－qi－jj－kk，其范數記為：

四元數小波變換的思想是將圖像進行多分辨率分解，得到不同空間、頻率的子圖像，再對系數選擇合適的方法進行處理。設二維信號(,)的四元數解析信號[11]為：

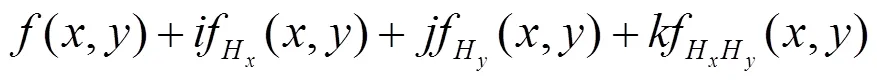
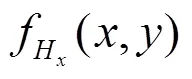
設一維小波函數的尺度函數和小波函數分別為h()，h()：

記(,)＝h()h()＋g()h()＋h()g()＋g()g()為2(2;)空間的四元數小波尺度函數，同時記：

為2(2;)空間的四元數小波函數。則對于"(,)?2(2;)，令c,k,m＝((,),,k,m(,))，d,k,m＝((,),,k,m(,))（＝1, 2, 3,,,?），則稱d,k,m（＝1,2, 3）為(,)的離散四元數小波變換。在文獻[16]中詳細講解了雙數復小波及四元數小波的分解和合成算法。

1.2 QWT域圖像去噪算法

多分辨率分析是圖像去噪中常用的經典方法，在以往的圖像處理算法中，很多學者只單純處理小波變換后的高頻子帶部分，而忽略低頻子帶系數認為其不含任何噪聲，使得處理后的圖像視覺效果不是很理想。因此，本文對圖像進行QWT分解后，兼顧低頻和高頻子帶系數特征，首先對低頻子帶采用快速雙邊濾波[17-18]算法；然后在高頻子帶基于MAP估計準則用NIG模型對分解系數進行建模，得到相應的閾值公式；最后結合OLI-Shrink算法實現圖像去噪。

1.2.1 NIG模型

NIG模型[12]主要是由逆高斯和不同均值高斯分布混合構建而成，理論上NIG模型可以描述任何形狀的曲線，則可以作為QWT變換系數的先驗分布，且其概率密度函數記為：

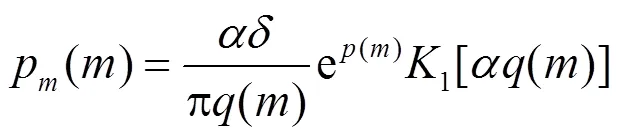
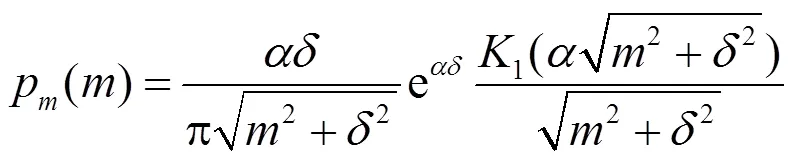
由于圖像通常由一些平滑區域和細節豐富區域組成，對于平滑區域，其四元數小波變換系數趨近于零值，對于紋理豐富區域，其變換系數會具有較大的幅值，因此非高斯分布特性是圖像變換系數的一個重要統計特征，它們呈現出零均值，重拖尾的特點。NIG模型可以靈活選擇模型參數用來準確描述具有不同拖尾形狀的數據屬性，因此NIG模型可以作為QWT高頻系數的先驗分布并對其進行建模。為了檢驗使用NIG模型作為四元數變換后系數分布的先驗模型的合理性，我們分別使用紋理結構較為豐富的圖像（Barbara）及紋理較少、對比度較低的紅外圖像（Plane）作為擬合示例，圖1是結果圖。圖中顯示的是Barbara圖像及Plane圖像經3層QWT分解的第3層水平方向的實部系數直方圖分布結果以及分別用NIG和GGD擬合這個概率密度函數結果。從圖1中我們可以看出，NIG模型可以準確地對這一高頻系數分布進行擬合，特別是重拖尾部分。NIG模型分布在零值附近呈現出尖銳的峰值，在峰值兩端表現出很長的拖尾特點，這與高頻系數的分布特點非常接近，這種高度擬合情形也同樣出現在其他的高頻子帶中。在其他測試圖像中也出現了相似的系數分布直方圖擬合結果，這再次證明了我們假定NIG為圖像的系數先驗分布的合理性。

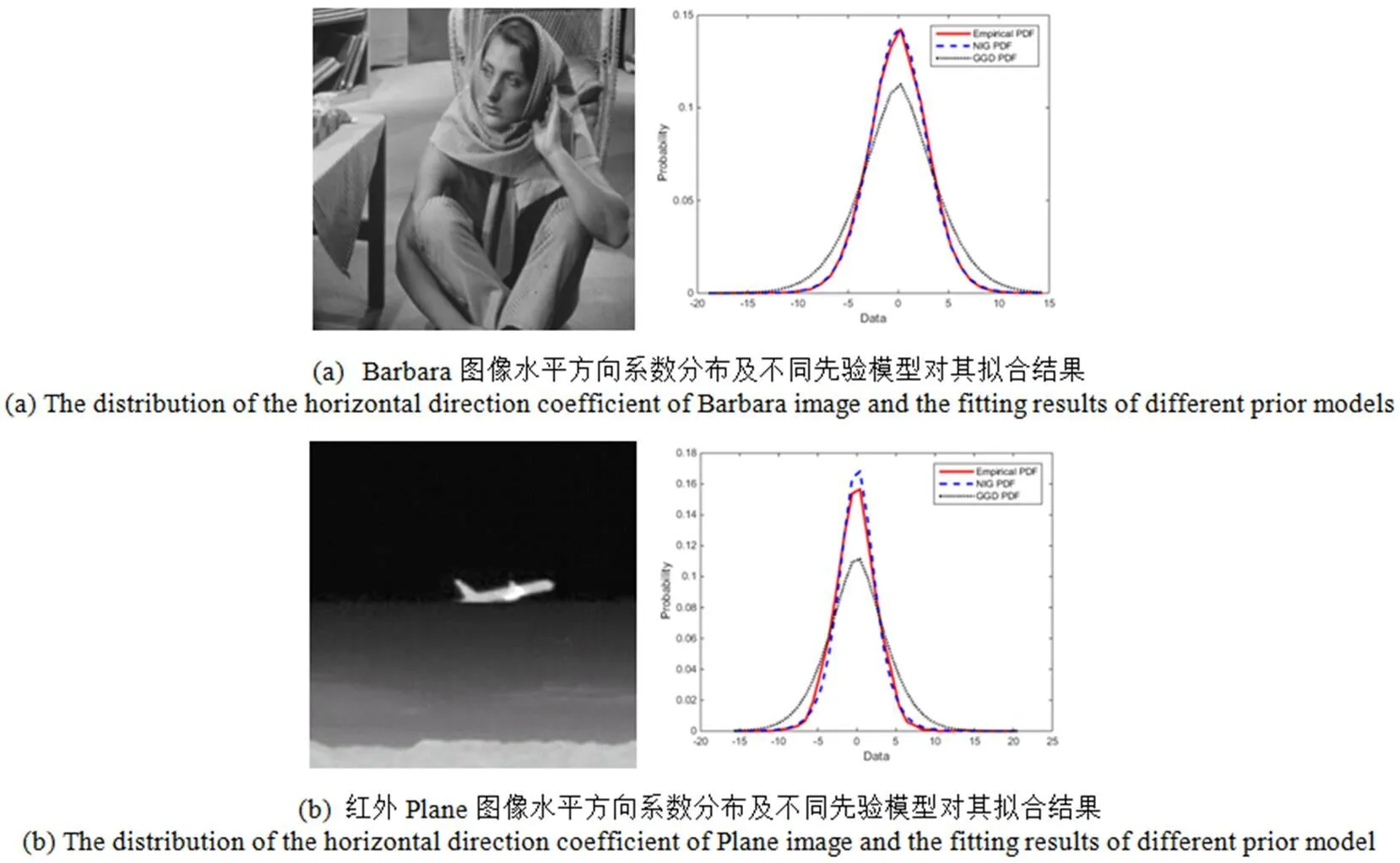
圖1 不同先驗模型擬合結果

1.2.2 貝葉斯最大先驗概率估計

設原始圖像(,)，含噪圖像(,)，(,)是均值為零，方差為2的高斯白噪聲，且滿足＝＋。經過QWT變換后，得到系數：

＝＋(6)

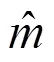
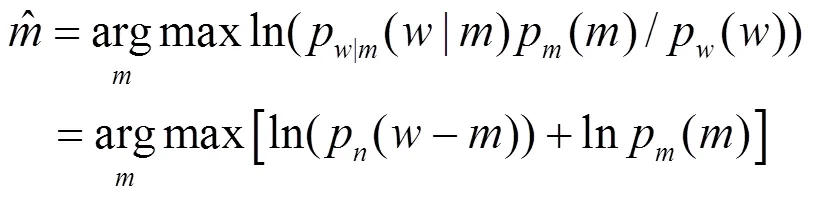
由假設知噪聲服從高斯分布，則其概率密度函數為：

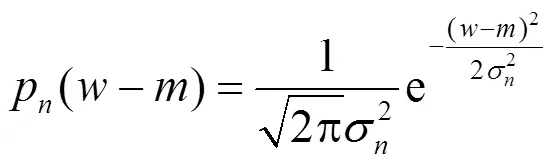
通過求導并結合文獻[15]得出的估計解為：

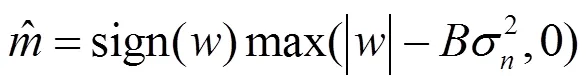
利用(9)式進行圖像去噪時需要在每個子帶估計參數和，可以自適應的在所有子帶中去除噪聲，同時(9)式類似于經典的軟閾值函數，閾值函數2的值依據QWT變換后系數。

1.2.3 參數估計

用(9)式進行圖像去噪時需要估計NIG模型的參數、及噪聲方差2，其中2可以用第一層小波分解對角子帶估計得到：

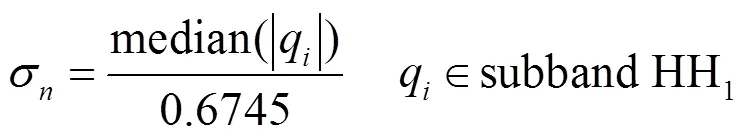
式中：HH1為第一層小波分解對應的高頻子帶，參數、根據不同的分解系數進行估計。

1.3 閾值算法

基于小波變換的閾值去噪主要通過設定一個特定的值，將大于閾值的系數去除以達到去噪的效果，可以應用到很多變換域中，比如四元數小波變換域。經典的閾值函數有硬閾值函數，軟閾值函數等，使用硬閾值公式時令分解后系數小于特定閾值的部分為零，硬閾值準則為：

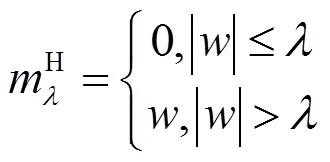
軟閾值準則為：

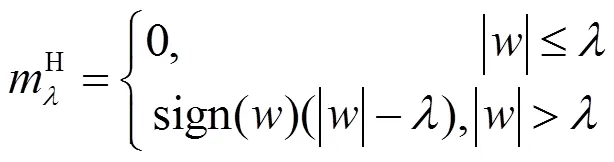
軟閾值函數比硬閾值函數更加實用有效，但對于大的系數很難選擇合適的最優閾值，Fathi和Nilchi[19]應用最優線性插值給出一種新的閾值算法（OLI-Shrink）：

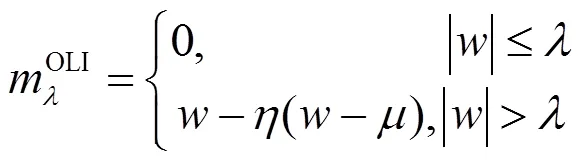
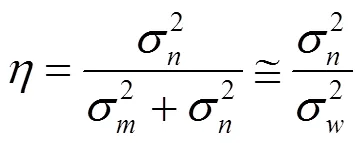
1.4 算法的主要步驟

Step 1：對含噪圖像進行3層QWT變換，得到高頻子帶和一系列的低頻子帶；

Step 2：低頻子帶采用快速雙邊濾波算法進行處理；

Step 3：采用(10)式估計噪聲標準，正態逆高斯模型的參數、采用(11)式估計；

Step 4：利用(9)式估計閾值函數中的變量，再通過(14)式估計系數；

Step5：最后進行逆QWT變換，得到去噪圖像。

2 實驗結果與分析

為了驗證本文提出的去噪算法在去除加性高斯白噪聲時的可行性和有效性，我們分別對自然圖像Lena、Barbara、紅外圖像Plane及遙感圖像（Pentagon）進行測試，加入零均值、方差為2的高斯白噪聲。在仿真實驗中，將本文所提的去噪算法與Mihcak等人[20]提出的LAWML算法，非下采樣Contourlet變換[21]（NSCT）算法、基于雙樹復小波（DT-CWT）的雙變量收縮（BiShrink）[22]算法、四元數小波變換域的Bayesian閾值算法（BQWT）[23]以及SURE-LET[24]進行比較；然后使用峰值信噪比（PSNR）、平均結構相似性[25]（MSSIM）以及去噪后的視覺效果結合起來評價本文方法。其中峰值信噪比定義為：

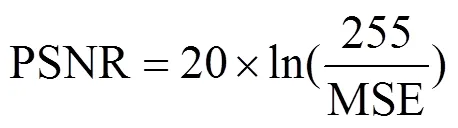
式中：、分別為原始圖像和降噪圖像；2為圖像大小，下面給出實驗結果。

圖2～圖4為含高斯噪聲標準差為20的自然圖像（Barbara）、紅外圖像（Plane）及遙感圖像（Pentagon）采用不同方法得到的去噪效果圖。從圖中可以看出，相比較于其他去噪方法，本文方法表現出更加優秀的抑制噪聲的性能，得到的圖像視覺效果更好。LAWML方法和SURE-LET方法去除噪聲不夠徹底，圖像中仍存在一些噪聲；NSCT方法可以有效地去除圖像噪聲，但是紋理信息丟失嚴重，邊界信息不能很好地得到保留；BiShrink方法和BQWT方法得到的去噪圖像出現了嚴重的塊效應，在邊界處存在較為嚴重的偽Gibbs現象；本文所提算法可以有效地去除噪聲，圖像的邊緣及紋理信息可以有效地保留，偽Gibbs現象得到很好的抑制。

圖2 噪聲方差為20的圖像（Barbara）去噪后局部放大圖

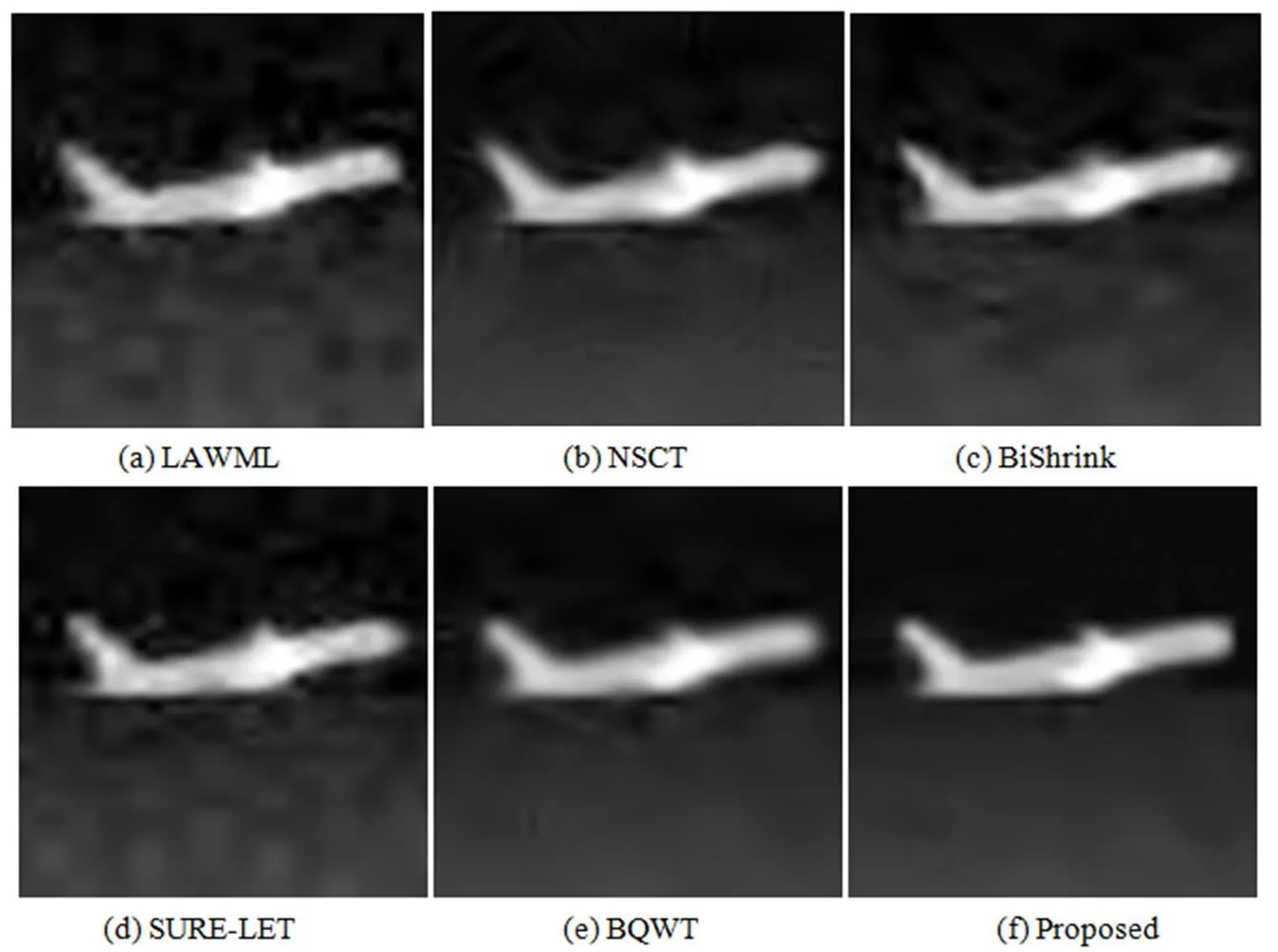
圖3 噪聲方差為20的紅外圖像（Plane）去噪后局部放大圖

圖4 噪聲方差為20的遙感圖像（Pentagon）去噪后局部放大圖

從圖5可以看出，隨著噪聲方差的增加，PSNR值存在一個下降的趨勢。對于不同的含噪圖像，在所有方法中本文方法取得了最大的PSNR值。與LAWML及SURE-LET方法相比，本文方法獲得的PSNR值有較大的提高，特別是對紅外圖像Plane和遙感圖像Pentagon，本文方法獲得的PSNR值的優勢較為明顯；相比于其他幾種去噪方法，本文方法去噪后的PSNR也有不同幅度的提升，這主要是因為所提算法處理高頻噪聲時的閾值合適，此外對低頻噪聲也有相關對策，這些處理都為抑制噪聲作了貢獻。

平均結構相似性可以用來評估去噪算法保留邊界信息的能力，因此我們在實驗中也使用了平均結構相似性作為客觀度量。不同方法處理不同噪聲等級圖像得到的客觀數據如表1所示。在表1中，本文去噪后的平均結構相似性是最高的，這表明了本文方法去噪后的圖像保持原圖像的結構能力是最高的。

3 結束語

本文在QWT小波域基于快速雙邊濾波和NIG模型提出一種新的圖像去噪算法，充分考慮小波變換后低頻和高頻子帶中的噪聲情況。低頻子帶采用快速雙邊濾波算法進行處理，去除低頻子帶中的噪聲；高頻子帶采用最優線性插值閾值算法（OLI-shrink）進行處理，其中該算法中的閾值函數是通過對子帶系數應用NIG模型建模并結合MAP估計準則推導給出的，由于NIG模型中參數的自適應性，使得OLI-shrink算法中閾值也具有相應的自適應性，提高了去噪后圖像質量。實驗結果顯示，本文算法在主觀視覺效果和客觀評價（PSNR，MSSIM）上都取得明顯的改進，達到一定的去噪效果并充分保留原始圖像的細節信息，說明本文算法的有效性。

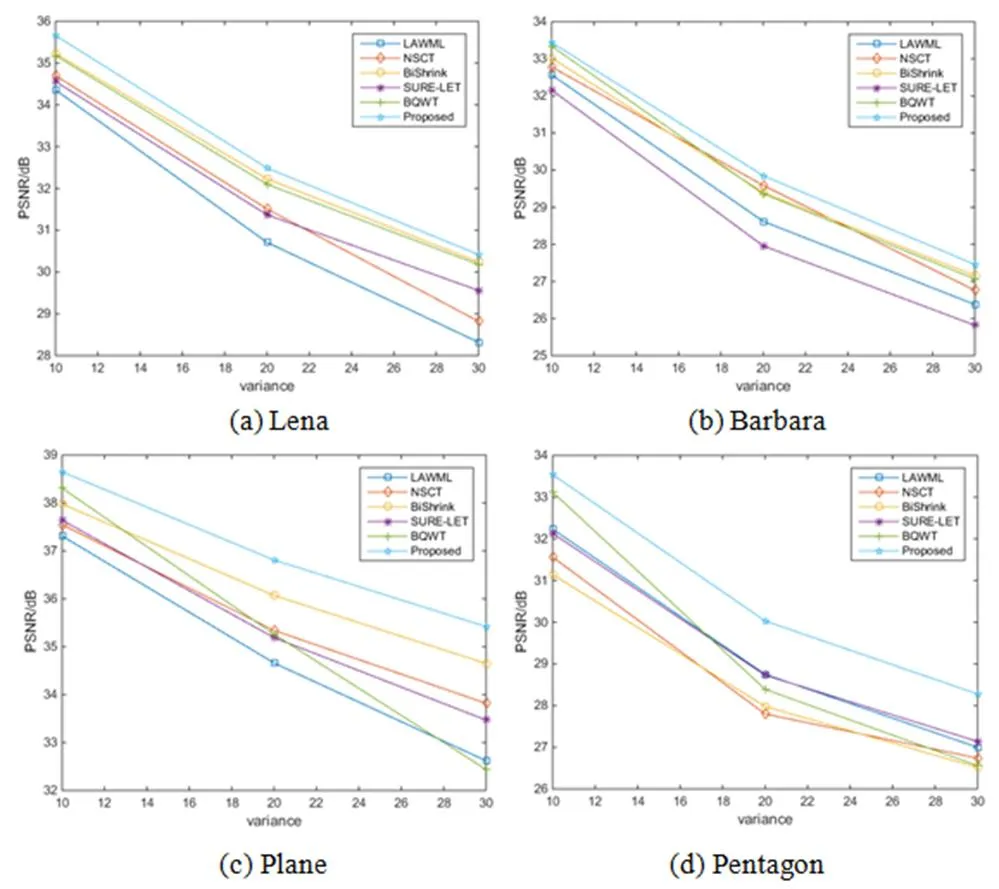
圖5 不同圖像去噪性能對比

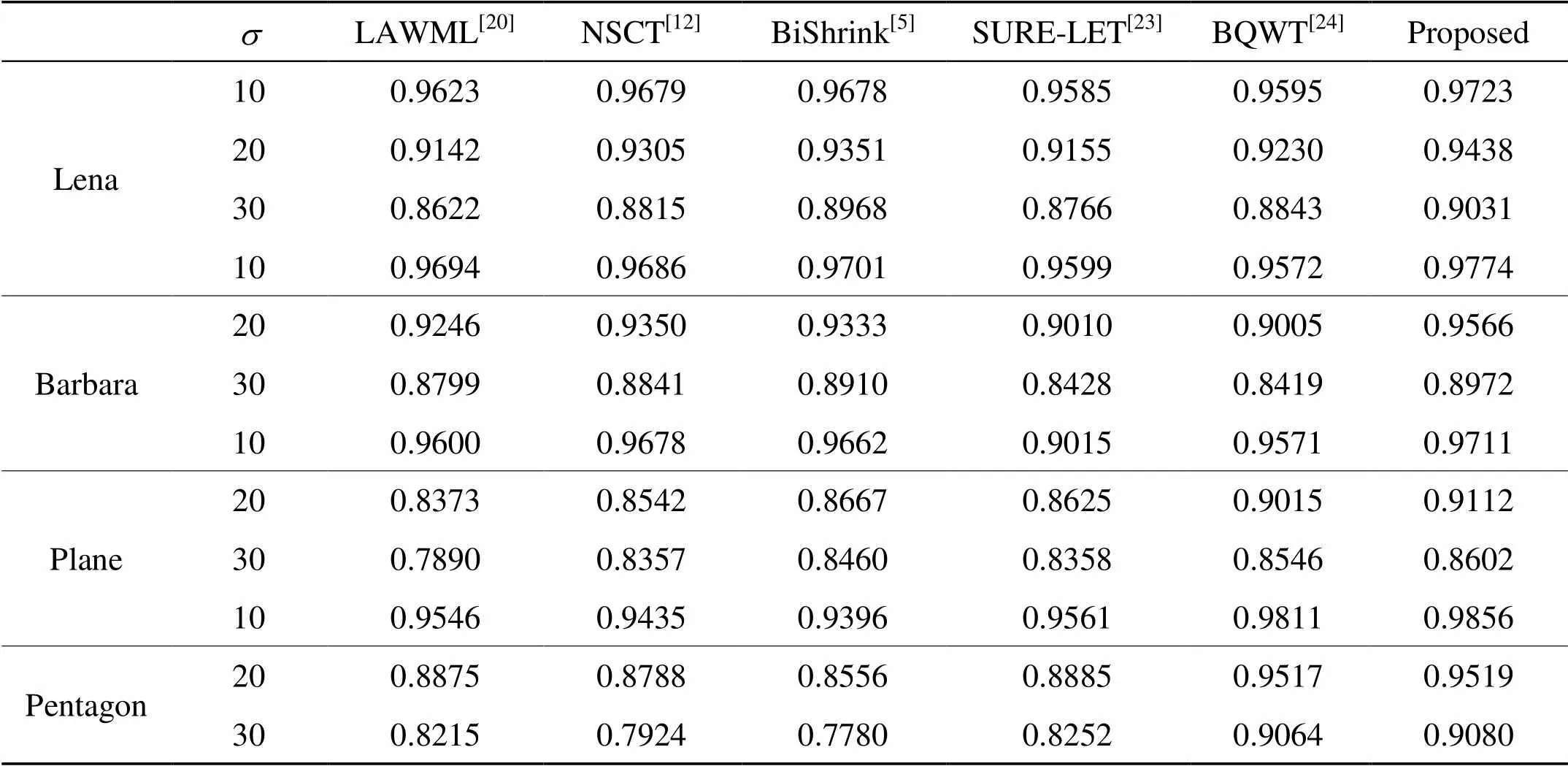
表1 不同方法對不同圖像去噪后的平均結構相似性（MSSIM）

[1] Donoho D L, Johnstone I M. Ideal spatial adaptation via wavelet shrinkage[J]., 1994, 81(3): 425-455.

[2] Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]., 1995, 90(432): 1200-1224.

[3] Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]., 2005, 22(6): 123-151.

[4] CHANG S G,YU B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]., 2000, 9(9): 1532-1546.

[5] Portilla J, Strela V, Wainwright M, et al. Image denoising using scale mixtures of gaussians in the wavelet domain[J]., 2003, 12(11): 1338-1351.

[6] Sendur L, Selesnick I W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency[J]., 2002, 50(11): 2744-2756.

[7] Cho D, Bui T D. Multivariate statistical for image denoising using wavelet transforms[J]., 2005, 20(1): 77-89.

[8] Cunha A L, ZHOU J P, DO M N. The nonsubsampled contourlet transform: theory design and application[J]., 2006, 15(10): 3089-3101.

[9] GUO K, Labate D. Optimally sparse multidimensional representation using shearlets[J]., 2007, 39(1): 298-318.

[10] Chan W L, Choi H, Baraniuk R G. Coherent multiscale image processing using dual-tree quaternion wavelets[J]., 2008, 17(7): 1069-1082.

[11] Moulin P, LIU J. Analysis of multiresolution image denoising schemes using generalized Gaussian and complexity priors[J]., 1999, 45(3): 909-919.

[12] 賈建, 陳莉. 基于正態逆高斯模型的非下采樣Contourlet變換圖像去噪[J]. 電子學報, 2011, 39(7): 1563-1568.

JIA Jian, CHEN Li. Using normal inverse Gaussian model for image denoising in NSCT domain[J]., 2011, 39(7): 1563-1568.

[13] Barndorff-nielesn O E. Normal inverse Gaussian distribution and stochastic volatility modeling[J]., 1997, 24(1): 1-13.

[14] Chaudhury K N. Acceleration of the shiftable O(1) algorithm for bilateral filtering and non-local means[J]., 2013, 22(4): 1291-1300.

[15] Corrochano E B. Multi-resolution image analysis using the quaternion wavelet transform[J]., 2005, 39(1): 35-55.

[16] Selesnick I W, Kingsbury N G, Baraniuk R B. The dual-tree complex wavelets transform[J]., 2005(11):123-151.

[17] Bulow T. Hypercomplex spectral signal representations for the processing and analysis of images[D]. Kiel, Germany: Christian Albrechts Univ., 1999.

[18] Bhuiyan M I H, Ahmad M O, Swamy M N S. Wavelet based despeckling of medical ultrasound images with the symmetric normal inverse Gaussian prior[C]//,, 2007: I-721-I-724.

[19] Fathi A, Naghsh-Nilchi A R. Efficient image denoising method based on a new adaptive wavelet packet thresholding function[J]., 2012, 21(9): 3981-3990.

[20] Mihcak M K, Kozintsev M, Ramchandran I K. Low-complexity image denoising based on statistical modeling of wavelet coefficients[J]., 1999, 6(12): 300-303.

[21] 劉炳良. 一種小波域改進雙邊濾波的水果圖像去噪算法[J]. 紅外技術, 2014, 36(3): 196-199.

LIU Bingliang. A new improved bilateral filtering algorithm for the fruit image based on wavelet transform domain[J]., 2014, 36(3): 196-199.

[22] Crouse M S, Nowak R D, Baraniuk R G. Wavelet-based statistical signal processing using hidden Markov models[J]., 1988, 46(4): 886-902.

[23] YIN Ming, LIU Wei, SHUI Jun, et al. Quaternion wavelet analysis and application in image denoising[J]., 2012, 18(6): 587-612.

[24] Luisier F, Blu T, Unser M.A new SURE approach to image denoisng: interscale orthonormal wavelet thresholding[J]., 2007, 16(3): 593-606.

[25] ZHOU W, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]., 2004, 13(4): 600-612.

New Image Denoising Algorithm Based on NormalInverse Gaussian Model in Quaternion Wavelet Domain

ZHU Fang1，LIU Wei2

(1.,,230088,; 2.,,230031,)

This paper proposes a novel image denoising algorithm based on the normal inverse Gaussian model and fast bilateral filtering in the quaternion wavelet transform domain. The quaternion wavelet transform is utilized to decompose a noised image. The fast bilateral filtering algorithm is used to deal with the low frequency sub-band coefficients. The normal inverse Gaussian model for the prior model is used to describe the distributions of the image’s high frequency coefficients. Its corresponding threshold function is then derived using Bayesian maximum a-posteriori probability estimation theory. Finally, an optimal linear interpolation thresholding algorithm is employed to guarantee a gentler thresholding effect. Experimental results show that the proposed method outperforms other existing state-of-the-art denoising methods in terms of peak signal-to-noise and mean structural similarity.

quaternion wavelet transform，bilateral filtering，normal inverse Gaussian model，Bayesian maximum posterior estimation，optimal linear interpolation，image denoising

TP391

A

1001-8891(2017)10-0928-08

2017-03-08；

2017-04-07.

朱芳（1987-），女，碩士，講師，研究方向為數字圖像處理。

安徽省高等學校自然科學研究重點項目（KJ2016A310）；安徽新華學院《概率論與數理統計A》教改課程項目（2015jgkcx11）；安徽科技學院校級項目（ZRC2016499）。