斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距原理可行性

肖榮康，王雨時(shí)，王曉鵬，聞 泉，張志彪

(南京理工大學(xué)機(jī)械工程學(xué)院，江蘇 南京 210094)

斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距原理可行性

肖榮康，王雨時(shí)，王曉鵬，聞 泉，張志彪

(南京理工大學(xué)機(jī)械工程學(xué)院，江蘇 南京 210094)

針對(duì)引信計(jì)時(shí)定距方法精度受彈丸初速影響大的問(wèn)題，提出斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距方法。該方法對(duì)初速變化造成的定距誤差可忽略不計(jì)，彈丸無(wú)需膛口測(cè)速。數(shù)值計(jì)算結(jié)果表明，彈重和射角變化對(duì)計(jì)轉(zhuǎn)數(shù)定距精度影響很小，但尾翼斜切角變化的影響較大。盡可能加大尾翼斜切角可提高計(jì)轉(zhuǎn)數(shù)定距精度，并降低尾翼斜切角制造誤差對(duì)定距精度的影響。低轉(zhuǎn)速?gòu)椡栌?jì)轉(zhuǎn)數(shù)定距原則上只適用于殺傷威力較大的中大口徑彈丸。

引信；計(jì)轉(zhuǎn)數(shù)定距；尾翼彈；斜切尾翼；外彈道

0 引言

精確控制炸點(diǎn)是提高彈藥打擊精度和殺傷效能的重要手段之一。利用引信裝定實(shí)現(xiàn)彈丸定距起爆控制的原理，一般有兩種類(lèi)型，一是裝定彈丸飛行時(shí)間信息，二是裝定彈丸飛行轉(zhuǎn)數(shù)信息。引信采用定時(shí)方法實(shí)現(xiàn)定距時(shí)其精度受初速影響較大，而計(jì)轉(zhuǎn)數(shù)定距無(wú)需膛口測(cè)速，精度較高[1]。目前由武器身管膛線(xiàn)賦予旋轉(zhuǎn)的旋轉(zhuǎn)穩(wěn)定彈丸引信通過(guò)計(jì)轉(zhuǎn)數(shù)定距技術(shù)研究已較為成熟。旋轉(zhuǎn)穩(wěn)定彈丸計(jì)轉(zhuǎn)數(shù)定距的基本原理是：對(duì)于飛行過(guò)程中由旋轉(zhuǎn)穩(wěn)定且彈道平直的彈丸，飛行經(jīng)過(guò)的距離正比于彈丸轉(zhuǎn)過(guò)的轉(zhuǎn)數(shù)，與炮口速度無(wú)關(guān)，因此可通過(guò)計(jì)測(cè)彈丸轉(zhuǎn)數(shù)實(shí)現(xiàn)彈丸定距起爆[2]。對(duì)計(jì)轉(zhuǎn)數(shù)引信研究起步較早的是俄羅斯，他們根據(jù)章動(dòng)計(jì)轉(zhuǎn)數(shù)原理設(shè)計(jì)出了電子計(jì)轉(zhuǎn)數(shù)引信[3]。文獻(xiàn)[4]分析了旋轉(zhuǎn)彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距原理的可行性，證明了低伸彈道在超音速段和亞音速段旋轉(zhuǎn)彈丸引信計(jì)轉(zhuǎn)數(shù)定距原理是成立的。文獻(xiàn)[5]聯(lián)立求解六自由度剛體彈道方程組和轉(zhuǎn)數(shù)計(jì)算方程，結(jié)果表明，射角變化、初速誤差、發(fā)射時(shí)藥溫變化、彈道上橫風(fēng)對(duì)計(jì)轉(zhuǎn)數(shù)定距精度影響較小；初始擾動(dòng)、彈道上氣壓、氣溫變化和縱風(fēng)等對(duì)計(jì)轉(zhuǎn)數(shù)定距精度影響較大。

對(duì)于尾翼彈，為了提高射擊精度，除了要具備恰當(dāng)?shù)姆€(wěn)定儲(chǔ)備量之外，往往還應(yīng)該使尾翼彈在飛行中伴之以低速轉(zhuǎn)動(dòng)。利用空氣動(dòng)力使尾翼彈旋轉(zhuǎn)常用的方法有兩種：尾翼斜置法和翼平面斜切法。尾翼斜置法是使尾翼片平面與彈軸呈一傾斜角；翼平面斜切法則是將尾翼片兩面中的一面削去一部分，使削面與彈軸呈一傾斜角[6]。對(duì)于這兩種不同的尾翼設(shè)計(jì)方法，賦予彈丸旋轉(zhuǎn)的原理相同。在迎面氣流作用下，彈丸每一對(duì)尾翼在對(duì)稱(chēng)位置上產(chǎn)生大小相等、方向相反的升力，其合力為零，力偶構(gòu)成導(dǎo)轉(zhuǎn)力矩使彈丸繞其幾何軸線(xiàn)旋轉(zhuǎn)，轉(zhuǎn)速?gòu)?開(kāi)始逐漸增大，至近似穩(wěn)定轉(zhuǎn)速(平衡轉(zhuǎn)速)。尾翼穩(wěn)定彈與旋轉(zhuǎn)穩(wěn)定彈探測(cè)轉(zhuǎn)速的技術(shù)原理相同。目前尚未見(jiàn)有文獻(xiàn)研究尾翼彈計(jì)轉(zhuǎn)數(shù)定距系統(tǒng)方法。本文針對(duì)此問(wèn)題，提出了斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距方法。

1 斜切尾翼彈外彈道轉(zhuǎn)數(shù)理論計(jì)算

1.1 數(shù)學(xué)模型

彈丸飛行過(guò)程中的轉(zhuǎn)數(shù)與彈丸轉(zhuǎn)速變化規(guī)律有關(guān)，其轉(zhuǎn)數(shù)計(jì)算公式為：

(1)

(2)

式中，C為彈丸極轉(zhuǎn)動(dòng)慣量。

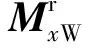
(3)

式中，λ1為尾翼之間相互影響對(duì)導(dǎo)轉(zhuǎn)力矩的修正因子，λ2為彈體直徑對(duì)導(dǎo)轉(zhuǎn)力矩的修正因子，n為尾翼的對(duì)數(shù)，zg為彈丸尾翼附加法向力的作用點(diǎn)到彈軸的距離，

(4)

由尾翼斜切角產(chǎn)生的附加法向力

(5)

對(duì)于有限翼展尾翼，當(dāng)翼型和翼面形狀確定后，不論亞音速或超音速，尾翼的升力系數(shù)導(dǎo)數(shù)為

(6)

則導(dǎo)轉(zhuǎn)力矩

(7)

導(dǎo)轉(zhuǎn)力矩系數(shù)

(8)

當(dāng)尾翼彈繞彈軸旋轉(zhuǎn)時(shí)，彈丸受到的極阻尼力矩是彈體極阻尼力矩和尾翼極阻尼力矩之和。彈體的極阻尼力矩系數(shù)為：

(9)

式中，ηλ為形狀修正系數(shù)，ηM為壓縮性修正系數(shù)，(CxfP)M=0為未計(jì)及形狀影響和壓縮性影響的平板摩阻系數(shù)，可按文獻(xiàn)[6]由雷諾數(shù)ReL計(jì)算得到。

由于雷諾數(shù)

(10)

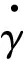
(11)

尾翼的極阻尼力矩系數(shù)為：

(12)

(13)

斜切尾翼彈丸的極阻尼力矩可寫(xiě)成

(14)

由上述分析知，斜切尾翼彈丸的導(dǎo)轉(zhuǎn)力矩和極阻尼力矩與彈丸的速度和角速度有關(guān)。若考慮彈丸速度的衰減，則自然坐標(biāo)系下的彈丸質(zhì)心運(yùn)動(dòng)方程組為[10]：

(15)

聯(lián)立式(1)、式(2)和方程組(15)，就可計(jì)算彈丸飛行過(guò)程中與飛行距離x對(duì)應(yīng)的轉(zhuǎn)數(shù)N。

1.2 模型求解

某大口徑滑膛炮榴彈的尾翼外形如圖1所示。

(17)

(18)

(19)

(20)

表1 彈丸和尾翼外形計(jì)算用參數(shù)

表2 靶場(chǎng)試驗(yàn)初始來(lái)流參數(shù)

表3 工程計(jì)算用修正系數(shù)[8-9]

1.3 模型驗(yàn)證

為保證外彈道計(jì)算可信性，需驗(yàn)證外彈道計(jì)算用參數(shù)。以某大口徑滑膛炮榴彈為例，已知該彈在14°射角時(shí)最大射程為9 600m。將初始條件v0=850m/s、θ0=14°、x0=0、y0=0代入式(16)，計(jì)算得最大射程xmax=9 780m，與已知試驗(yàn)值相對(duì)誤差為1.88%，說(shuō)明計(jì)算可信。

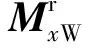
表4 測(cè)試轉(zhuǎn)速與理論計(jì)算轉(zhuǎn)速對(duì)比及誤差

理論計(jì)算所得彈丸轉(zhuǎn)速變化曲線(xiàn)與試驗(yàn)測(cè)量值對(duì)比如圖2所示。由表4及圖2知，彈丸在試驗(yàn)點(diǎn)處的轉(zhuǎn)速理論計(jì)算值與試驗(yàn)值有25%左右的相對(duì)誤差。該誤差可能主要是由攻角影響造成的。但理論計(jì)算得到的轉(zhuǎn)速變化規(guī)律與試驗(yàn)值在彈丸轉(zhuǎn)速上升階段趨勢(shì)一致，而彈丸轉(zhuǎn)速的上升與衰減均由導(dǎo)轉(zhuǎn)力矩和極阻尼力矩作用所致，說(shuō)明表1至表3所列外彈道計(jì)算參數(shù)可用。因此使用理論和數(shù)值分析模型研究斜切尾翼彈丸引信計(jì)轉(zhuǎn)數(shù)定距系統(tǒng)原理是可行的。

2017年韓國(guó)化妝品對(duì)中國(guó)大陸出口同比增長(zhǎng)23.1%，達(dá)129億元。而經(jīng)過(guò)一年的調(diào)整，以愛(ài)茉莉太平洋及LG生活健康為代表的韓妝企業(yè)迎來(lái)了新的曙光。2018年第二季度，二者化妝品業(yè)務(wù)銷(xiāo)售額及營(yíng)業(yè)利潤(rùn)均達(dá)到雙位數(shù)增長(zhǎng)，高端品牌表現(xiàn)亮眼。

2 計(jì)轉(zhuǎn)數(shù)定距原理及特點(diǎn)

以初速v0=850 m/s、射角θ0=1°、尾翼斜切角β=6.24為初始條件對(duì)模型進(jìn)行數(shù)值計(jì)算，得彈丸轉(zhuǎn)數(shù)N與水平距離x的關(guān)系如圖3所示。由圖3知，斜切尾翼彈丸出炮口后受導(dǎo)轉(zhuǎn)力矩作用加速旋轉(zhuǎn)，此時(shí)彈丸轉(zhuǎn)速較低，因而N-x曲線(xiàn)的斜率較大，且曲線(xiàn)斜率隨著轉(zhuǎn)數(shù)增加逐漸減小。當(dāng)彈丸達(dá)到平衡轉(zhuǎn)速后，斜切尾翼彈飛行距離與轉(zhuǎn)數(shù)的關(guān)系與旋轉(zhuǎn)穩(wěn)定彈相似，基本呈線(xiàn)性關(guān)系。在曲線(xiàn)的初始段，彈丸旋轉(zhuǎn)一周對(duì)應(yīng)的水平距離較大，若此階段應(yīng)用計(jì)轉(zhuǎn)數(shù)定距會(huì)導(dǎo)致定距精度較低，故斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距應(yīng)在彈丸達(dá)到平衡轉(zhuǎn)速之后。

3 初速變化對(duì)計(jì)轉(zhuǎn)數(shù)定距的影響

針對(duì)由武器身管膛線(xiàn)賦予旋轉(zhuǎn)的彈丸，文獻(xiàn)[1]以彈丸初速波動(dòng)3%在不同射程上進(jìn)行外彈道仿真，結(jié)果表明，在相同水平距離上彈丸初速變化對(duì)轉(zhuǎn)數(shù)的影響很小，計(jì)轉(zhuǎn)數(shù)定距精度能滿(mǎn)足精確定距要求。對(duì)于加農(nóng)炮，初速散布約為0.15%v0至0.2%v0[12]。為探究斜切尾翼彈丸初速對(duì)計(jì)轉(zhuǎn)數(shù)定距的影響，以彈丸初速v0=850 m/s、射角θ0=1°、初速變化△v0=±10 m/s(變化率為1.18%)按前述理論方法進(jìn)行外彈道仿真，得彈丸在轉(zhuǎn)數(shù)N分別為49、79、109時(shí)對(duì)應(yīng)的水平距離如表5所列。

表5 彈丸初速變化在不同轉(zhuǎn)數(shù)下的水平距離

由表5知，在同一轉(zhuǎn)數(shù)下，彈丸初速越大，對(duì)應(yīng)水平距離也越大。彈丸初速變化在10 m/s內(nèi)轉(zhuǎn)數(shù)N=49時(shí)定距誤差△x≤2.1 m(約為0.21%)；轉(zhuǎn)數(shù)N=79時(shí)定距誤差△x≤1.6 m(約為0.11%)；轉(zhuǎn)數(shù)N=109時(shí)定距誤差△x≤1.0 m(約為0.05%)；定距誤差隨彈丸轉(zhuǎn)數(shù)的增加而減小。對(duì)于斜切尾翼彈丸，初速變化對(duì)計(jì)轉(zhuǎn)數(shù)定距的影響很小(只相當(dāng)于定時(shí)原理產(chǎn)生的距離誤差的1/24～1/6)，亦即斜切尾翼彈外彈道計(jì)轉(zhuǎn)數(shù)定距原理是成立的。

4 計(jì)轉(zhuǎn)數(shù)定距彈丸影響因素

由斜切尾翼彈外彈道轉(zhuǎn)數(shù)計(jì)算模型知，尾翼斜切角、彈重和射角等因素對(duì)計(jì)轉(zhuǎn)數(shù)定距有影響，其影響程度直接決定了計(jì)轉(zhuǎn)數(shù)定距原理的可行性。

4.1 尾翼斜切角影響分析

以彈丸初速v0=850 m/s、射角θ0=1°進(jìn)行數(shù)值計(jì)算，尾翼斜切角β=6.24°時(shí)在水平距離1 000 m、1 500 m、2 000 m處的近似轉(zhuǎn)數(shù)分別為49、79、109；尾翼斜切角β=12.48°時(shí)在水平距離1 000 m、1 500 m、2 000 m處的近似轉(zhuǎn)數(shù)分別為98、158、218。表6列出了尾翼斜切角β= 6.24°變化±15′時(shí)，彈丸在轉(zhuǎn)數(shù)N分別為49、79、109所對(duì)應(yīng)的水平距離。由表6知，尾翼斜切角β=6.24°變化±15′引起的定距誤差在彈丸飛行轉(zhuǎn)數(shù)N=49時(shí)約為33 m，N=79時(shí)定距誤差約為55 m，N=109時(shí)定距誤差約為76 m。表7為尾翼斜切角β=12.48°變化±15′時(shí)，彈丸在轉(zhuǎn)數(shù)N分別為98、158、218所對(duì)應(yīng)的水平距離。由表7知，尾翼斜切角β=12.48°變化±15′引起的定距誤差在彈丸飛行轉(zhuǎn)數(shù)N=98時(shí)約為16 m，N=158時(shí)定距誤差約為26 m，N=218時(shí)定距誤差約為36 m。因此，尾翼斜切角對(duì)計(jì)轉(zhuǎn)數(shù)定距精度的影響較大，由尾翼斜切角誤差造成的定距誤差隨轉(zhuǎn)數(shù)的增加而增大，加大尾翼斜切角可降低尾翼斜切角誤差對(duì)定距精度的影響。

表6 尾翼斜切角β =6.24°±15′時(shí)不同轉(zhuǎn)數(shù)對(duì)應(yīng)的水平距離

表7 尾翼斜切角β=12.48°±15′時(shí)不同轉(zhuǎn)數(shù)對(duì)應(yīng)的水平距離

4.2 彈重變化影響分析

(21)

4.3 射角變化影響分析

表9給出了彈丸初速v0=850 m/s、射角θ0從1°到10°變化時(shí)，水平距離分別為1 000 m、1 500 m、2 000 m處所對(duì)應(yīng)的彈丸轉(zhuǎn)數(shù)。從中可看出，彈丸在某一水平距離下的轉(zhuǎn)數(shù)隨射角的增大而增大。表10為彈丸初速v0=850 m/s、射角θ0從1°到10°變化時(shí)，轉(zhuǎn)數(shù)分別為49、79、109所對(duì)應(yīng)的水平距離。從中可看出，彈丸在某一確定轉(zhuǎn)數(shù)下的水平距離隨射角的增大而減小。而對(duì)于加農(nóng)炮，射角散布為0.2密位左右[12]。因此，在射角變化較小時(shí)，彈丸在某一距離上的轉(zhuǎn)數(shù)可視為定值，射角變化對(duì)計(jì)轉(zhuǎn)數(shù)定距精度的影響很小。

表8 彈重變化時(shí)不同轉(zhuǎn)數(shù)對(duì)應(yīng)的水平距離

表9 彈丸不同射角在水平距離1 000 m、1 500 m、2 000 m處的轉(zhuǎn)數(shù)

表10 彈丸不同射角在轉(zhuǎn)數(shù)49、79、109處的水平距離

5 改善斜切尾翼彈引信計(jì)轉(zhuǎn)數(shù)定距精度分析

由身管膛線(xiàn)賦予轉(zhuǎn)速的旋轉(zhuǎn)穩(wěn)定彈丸出炮口后自轉(zhuǎn)角速度很大，彈丸自轉(zhuǎn)一周(1轉(zhuǎn))對(duì)應(yīng)的水平距離很小，保證了引信計(jì)轉(zhuǎn)數(shù)定距精度。而斜切尾翼彈丸的自轉(zhuǎn)角速度較低，彈丸自轉(zhuǎn)一周對(duì)應(yīng)的水平距離較大，使得引信計(jì)轉(zhuǎn)數(shù)定距的精度較低。表11為彈丸初速v0=850 m/s、射角θ0=1°、尾翼斜切角β=6.24°在不同轉(zhuǎn)數(shù)變化下對(duì)應(yīng)的水平距離變化表。由表10知，彈丸轉(zhuǎn)數(shù)變化△N=±0.5時(shí)，水平距離變化△x約為±8.3 m。設(shè)轉(zhuǎn)數(shù)Ns對(duì)應(yīng)的水平距離為xs，則定距在xs±8.3 m范圍內(nèi)彈丸裝定轉(zhuǎn)數(shù)應(yīng)為Ns。若該彈丸的動(dòng)態(tài)殺傷半徑r≥8.3 m，則在忽略其他因素的情況下，計(jì)轉(zhuǎn)數(shù)定距精度可以滿(mǎn)足要求。

為提高斜切尾翼彈引信計(jì)轉(zhuǎn)數(shù)定距精度，應(yīng)在不影響彈丸飛行穩(wěn)定性的基礎(chǔ)上提高彈丸外彈道轉(zhuǎn)速。根據(jù)前述的斜切尾翼彈旋轉(zhuǎn)機(jī)理，可通過(guò)加大尾翼斜切角β使尾翼導(dǎo)轉(zhuǎn)力矩增大，從而提高彈丸外彈道轉(zhuǎn)速以提高計(jì)轉(zhuǎn)數(shù)定距精度。表12為彈丸初速v0=850 m/s、射角θ0=1°、尾翼斜切角β=9.36°(加大50%)在不同轉(zhuǎn)數(shù)變化下對(duì)應(yīng)的水平距離變化表。由表12知，彈丸轉(zhuǎn)數(shù)變化△N=±0.5時(shí)，水平距離變化△x約為±5.6 m，此時(shí)若彈丸的動(dòng)態(tài)殺傷半徑r≥5.6 m，則在忽略其他因素的情況下，計(jì)轉(zhuǎn)數(shù)定距精度能滿(mǎn)足要求，精度相比之前有較大提高。

表11 β=6.24°時(shí)彈丸轉(zhuǎn)數(shù)變化對(duì)應(yīng)的水平距離

表12 β=9.36°時(shí)彈丸轉(zhuǎn)數(shù)變化對(duì)應(yīng)的水平距離

6 結(jié)論

本文提出了斜切尾翼彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距方法。該方法對(duì)初速變化造成的定距誤差可忽略不計(jì)，彈丸無(wú)需膛口測(cè)速。數(shù)值計(jì)算結(jié)果表明彈重和射角變化對(duì)計(jì)轉(zhuǎn)數(shù)定距精度影響很小，但尾翼斜切角變化的影響較大。盡可能加大尾翼斜切角可提高計(jì)轉(zhuǎn)數(shù)定距精度，并降低尾翼斜切角制造誤差對(duì)定距精度的影響。為彌補(bǔ)斜切尾翼彈丸轉(zhuǎn)速低所導(dǎo)致的地磁探測(cè)誤差對(duì)定距精度的影響，彈丸動(dòng)態(tài)威力應(yīng)盡可能加大。低轉(zhuǎn)速?gòu)椡栌?jì)轉(zhuǎn)數(shù)定距原則上只適用于殺傷威力較大的中大口徑彈丸。

[1]沈波,賴(lài)百壇. 計(jì)轉(zhuǎn)數(shù)定距引信炸點(diǎn)散布精度分析[J]. 探測(cè)與控制學(xué)報(bào),2004,26(1):35-37.

[2]沈波,陳荷娟,王志興,等. 基于地磁傳感器的計(jì)轉(zhuǎn)數(shù)引信可行性研究[J]. 探測(cè)與控制學(xué)報(bào),2001,23(4):45-48.

[3]程翔,黃文良,陸靜. 自動(dòng)榴彈發(fā)射器引信及其計(jì)轉(zhuǎn)數(shù)方法[J]. 探測(cè)與控制學(xué)報(bào),2001,23(2):1-4.

[4]王雨時(shí). 旋轉(zhuǎn)彈引信外彈道計(jì)轉(zhuǎn)數(shù)定距原理研究[C]//中國(guó)兵工學(xué)會(huì)引信專(zhuān)業(yè)委員會(huì)引信技術(shù)創(chuàng)新研討會(huì)論文集. 西安：中國(guó)兵工學(xué)會(huì)引信專(zhuān)業(yè)委員會(huì)，2002.

[5]王中原,張比升,史金光,等. 炮彈記轉(zhuǎn)數(shù)定距影響因素分析[J]. 彈道學(xué)報(bào),2006,18(4):8-11.

[6]沈仲書(shū),劉亞飛. 彈丸空氣動(dòng)力學(xué)[M]. 北京:國(guó)防工業(yè)出版社,1984.

[7]《引信設(shè)計(jì)手冊(cè)》編寫(xiě)組. 引信設(shè)計(jì)手冊(cè)[M]. 北京:國(guó)防工業(yè)出版社,1978.

[8]張維權(quán),周南,詹德來(lái),等. 彈箭空氣動(dòng)力特性分析與計(jì)算[M]. 北京:國(guó)防工業(yè)出版社,1979.

[9]臧國(guó)才,李樹(shù)常. 彈箭空氣動(dòng)力學(xué)[M]. 北京:兵器工業(yè)出版社,1989.

[10]浦發(fā),芮筱亭. 外彈道學(xué)[M]. 北京:國(guó)防工業(yè)出版社,1989.

[11]王曉鵬. 某大口徑滑膛炮多功能彈彈底觸發(fā)引信相關(guān)技術(shù)研究[D]. 南京：南京理工大學(xué),2015.

[12]王兆勝. 射角和初速對(duì)地面密集度的影響[J]. 火炮發(fā)射與控制學(xué)報(bào),2008(4):1-4.

[13]鮑廷鈺,邱文堅(jiān). 內(nèi)彈道學(xué)[M]. 北京:北京理工大學(xué)出版社,1995.

Fin-stabilized Projectile Revolution Counting for Determining Distance

XIAO Rongkang，WANG Yushi，WANG Xiaopeng，WEN Quan，ZHANG Zhibiao

(School Of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094,China)

Aiming at the problem that the ranging and timing precision are quite influenced by initial velocity of projectile while the fuze uses the method of determining distance by counting time, a method of determining distance by counting revolution for fuze of fin-stabilized projectile with beveled fin in exterior ballistic trajectory was proposed. The error of determining distance caused by the variation of velocity could be ignored by using this method, and the initial velocity of projectile need not be measured. The results of numerical calculation indicated that variations of the mass of projectile and firing angle have very small effects on precision of determining distance by counting revolution, but the effect of the angle variation of beveled fin was larger. By increasing the angle of beveled fin as large as possible could improve the precision of determining distance by counting revolution and lower the effect of manufacturing error of the angle of beveled fin on the precision of determining distance. Determining distance by counting revolution of low rotation speed projectiles could only be applied to?medium?and?large?caliber projectiles which the lethality was relatively large in principle.

fuze; counting revolution determining distance; fin-stabilized projectile; beveled fin; exterior ballistic trajectory

2016-07-02

肖榮康(1992—)，男，江西贛州人，碩士研究生，研究方向：探測(cè)制導(dǎo)與控制。E-mail：xrk0924@163.com。

TJ43

A

1008-1194(2017)01-0013-07