優化的BP神經網絡在水輪機調節系統中的應用研究
譚 聯,許永強,楊沛源,楊超杰,劉萬康
(華北水利水電大學電力學院,鄭州 450000)
0 引 言
自PID控制器被提出以來,由于其結構簡單、易于操作、參數易于調整和控制精度可靠等優點,使得工程中各種先進控制過程或優化均是以PID控制回路為基礎。然而實際生產過程中被控對象多為結構復雜、參數時變的非線性動態系統,譬如,在水力發電行業中,水輪機調節系統就是一典型的具有變參數、非線性等特性的非最小相位系統,目前該調速器所采用的控制規律仍然是PID控制規律,但在實際生產運行中常規PID控制往往出現參數不易實時調整、自適應能力差、控制效果不佳等問題。
伴隨著水電在電力系統中比重的不斷增加,電網對水輪機調節系統的控制品質的要求也越來越高。所以,尋求更好的控制策略應用于該系統以獲得更好的動態過渡過程,獲得更安全、更優質的電能即是本文的研究重點。目前,水輪機組控制策略多側重于智能化控制方式的研究,但這些智能方式仍然存在著各種各樣的問題:模糊PID控制效果相較于常規PID控制雖有了明顯改善,但在較小偏差范圍內控制品質仍不能令人滿意[1];BP神經網絡PID控制除具有常規PID控制的基本特點,又擁有神經網絡自身固有的自適應、自學習的特性及任意非線性逼近的能力,使其能夠很好地實現在線參數調整,但由于BP神經網絡自身的缺陷,使其還存在著諸如收斂速度慢、易陷入局部極小等問題[2]。
主成份分析是研究在原始樣本數據(多變量)中如何通過少數幾個主成份來揭示原變量間的內部結構的方法,它的應用可以使神經網絡的輸入單元減少,進而使得網絡結構得到簡化,以此達到縮短網絡收斂時間、提高網絡的精度和穩定性的目的。
本文主要研究采用主成份分析對BP神經網絡進行優化[3,4],設計新的水輪機調節PID控制系統,并在MATLAB中完成M語言的編寫,進行實例仿真、分析。
1 基于主成份-BP神經網絡的水輪發電機組調節系統
1.1 主成份分析
1.1.1 主成份分析概念
主成份分析是多元統計分析中對樣本數據進行降維的最為常用的一種方法。其主要任務是利用數學算法將原來樣本數據庫中具有一定相關性的指標變量X1,X2,…,Xp(假如為p個變量),去除變量間多重共線性(相關性)重新組合成一組較少個數的綜合指標F1、F2、…、Fm(m 1.1.2 主成份分析計算步驟 假設原始數據有n個樣本,每個樣本有p個變量,構成一個n×p階的矩陣。 (1) 計算樣本相關系數矩陣。 (2) 矩陣中相關系數為: (3) 求出矩陣R的特征值λi和相應的正交化單位向量ai,前m個特征值λ就是前m個主成份對應的方差,ai便是主成份各個變量前的系數。即: Fi=a′iX (4) 選擇主成份:根據方差累積貢獻率G(m)的大小來確定最終選取的主成份個數。 (5) 當G(m)≥85%時,就可以認為新樣本能夠反映原來樣本的信息了,相應的取前m個主成分,即:F1、F2、…、Fm。 1.2.1 BP神經網絡PID控制結構 BP神經網絡PID控制(BPNN-PID)結構包括兩個部分[2]: (1)常規PID控制:直接對被控對象進行控制。仿真試驗中,其控制規律增量式為: (6) 式中:kp為比例系數;ki為積分時間常數;kd為微分時間常數;u(k)為k采樣時刻控制器輸出;rin(k)為k采樣時刻期望系統輸出值;yout(k)為k采樣時刻系統實際輸出值;e(k)為rin(k)與yout(k)所形成的偏差。 (2)BP神經網絡(BPNN):憑借神經網絡任意非線性逼近的能力,在誤差允許范圍內,根據給定期望輸出量、實際輸出量及二者所形成的偏差,逐層調整網絡系數以完成控制系統最優PID參數的整定。網絡輸出分別為參數kp,ki,kd。 1.2.2 主成份-BP神經網絡PID算法 (1)本文中BPNN確定為3層,常規BPNN-PID(網絡結構為4-5-3)輸入量為: X=[rin(k),yout(k),e(k),dec(k)]T (7) 式中:dec(k)為k采樣時刻系統偏差變化率。 在MATLAB中完成該方法程序的編寫并進行仿真試驗[5,6],整定出該方法下最優的kp,ki,kd參數組合,在學習、自適應過程中得到的矩陣X即為主成份分析的數學樣本。 (2)對矩陣X進行主成份分析,選取若干主成份與rin(k)組成新的樣本矩陣Xm+1: Xm+1=[rin(k),F1,F2,…,Fm]T (8) 將其作為網絡輸入量搭建新的BP神經網絡并進行仿真試驗,整定出該方法下控制系數的最佳組合,算法及步驟與常規BPNN-PID控制相同。 將上節中主成份-BP神經網絡-PID控制器應用于某水電廠混流式水輪發電機組,構成的控制系統如圖1所示[2,7],圖1中各部分傳遞函數為公式(9)~式(11)所示。 圖1 基于主成份-BP神經網絡的水輪發電機組調節系統結構圖Fig.1 Based on the principal component-BP neural network control system of hydroelectric generating set structure (9) (10) Gg(s)=1/(Tas+en) (11) 式中:Ty為接力器反應時間常數;Tw為水流慣性時間常數;Ta為機組慣性時間常數;ey、eh、eqy、eqh、en均為系統傳遞系數。 該機組調節系統的初始設計參數為:Ta=8.5 s,Tw=1.774 s,Tb=0.26Ta=2.21 s,en=1.0,Ty=0.3 s,選工況一(額定工況)和工況二(非額定工況)進行仿真計算。兩工況的水輪機傳遞系數如表1所示。 表1 兩工況點的水輪機傳遞系數Tab.1 Two point of the water turbine transfer coefficient 分別采用常規PID、BP神經網絡PID及主成份-BP神經網絡PID對上述兩個工況點的被控系統進行仿真分析、比較,常規PID參數值由Ziegler-Nichols方法整定[1]。 由Ziegler-Nichols整定方法得到該工況點下常規PID參數分別為:kp=11.02,ki=4.61,kd=6.59。 2.1.1 基于BP神經網絡的PID控制仿真[5] 設定η=0.2,α=0.01,網絡輸入為X=[rin(k),yout(k),e(k),dec(k)]T。 首先選取了一組隨機數作為權值、閾值: wi=[0.190 4,0.616 4,-0.042 2,0.099 6; 0.247 3,-0.224 1,-0.159 3,0.215 8; 0.607 7,-0.032 7,0.334 2,-0.236 5; -0.715 8,0.084 6,0.016 4,-0.066 8; 0.056 4,-0.097 0,-0.090 4,-0.130 9] wo=[0.227 5,-0.264 3,0.123 2,-0.424 9,-0.038 9; -0.418 4,-0.054 3,-0.404 1,0.392 0,0.125 5; 0.348 2,0.229 7,0.142 7,0.332 5,0.422 9] 仿真結果如圖2所示:采用PID控制,取kp=0.717 9,ki=0.179,kd=0.563 2。在simulink仿真給定頻率設定為50 Hz,給定頻率階躍跟蹤曲線如圖3所示。 圖2 參數自適應曲線Fig.2 The parameter adaptive curve 圖3 頻率給定階躍跟蹤曲線Fig.3 The frequency of a given step tracking curve 由圖3可以看出,相較于常規PID該控制系統具有嚴重的遲滯現象。所以采用高增益的PID控制器進行補償[8],加大比例系數kp=7.179,ki=1.79,kd=5.632進行仿真,能得到如圖4所示的跟蹤結果。 圖4 采用高增益PID控制時的階躍跟蹤曲線Fig.4 Step tracking curve with high gain PID control 由圖4可以看出,采用高增益的PID控制器進行補償時,跟蹤效果較前面有了很大改善,調節時間由常規PID控制系統的14.66 s降低到了13.75 s(穩態誤差允許范圍設定為|ess|≤0.2,下同),超調量也有了很大程度的降低。 2.1.2 主成份-BP神經網絡PID控制仿真 將2.1.1節BPNN-PID控制系統中實際輸出值yout(k)、誤差e(k)及誤差變化率dec(k)作為優化BP神經網絡的學習樣本,進行主成份分析(表2)(統計軟件SPSS 22.0中實現,數據略)。 表2 主成份貢獻率Tab.2 Principal component contribution rate 注:提取方法為主成份分析。 由表2可知得到3個主成份,根據選定的累積貢獻率,選取主成份F1、F2(包含了樣本數據93%的信息),并由表3中系數矩陣寫出相應主成份表達式。 表3 主成份系數矩陣Tab.3 Principal component coefficient matrix F1=-0.982yout(k)+0.982e(k)+0.401dec(k) (12) F2=0.187yout(k)-0.187e(k)+0.916dec(k) (13) 網絡輸入此時變為X3=[rin(k),F1,F2]T,網絡結構為3-5-3,選取初始連接權、閾值: wi=[0.574 3,-0.125 3,-0.012 6; 0.296 5,-0.153 6,0.434 4; -0.446 6,0.167 2,0.121 2; -0.453 4,0.035 5,0.457 2; -0.537 7,0.310 9,-0.235 8] wo=[0.153 8,0.172 8,-0.298 2,-0.177 8,-0.515 6; -0.233 2,-0.454 3,0.145 5,0.258 2,0.079 9; 0.149 5,-0.267 5,0.322 1,0.153 0,-0.135 5] 仿真結果如圖5所示。采用PID控制:kp=0.832,ki=0.224,kd=0.409在Simulink中仿真,同樣給定頻率設定為50 Hz,給定頻率跟蹤曲線如圖6所示。從圖6中可以看出,相較于常規PID該控制系統同樣出現了嚴重的遲滯現象,所以采用高增益的PID控制器進行補償,加大比例系數kp=8.32,ki=2.24,kd=4.09進行仿真。 圖5 優化后參數自適應曲線Fig.5 Parameter adaptive curve after optimization 將BP神經網絡PID控制系統優化前后仿真曲線放在同一張仿真圖里進行比較,如圖6所示(圖中主成份-BP神經網絡及BP神經網絡PID參數均為高增益比例參數,圖7亦同)。通過系統仿真對比可以看出(表4):系統采用主成份-BP神經網絡-PID控制方式后,調節系統的控制性能相較于BPNN-PID控制除了超調量略大,其他動態性能均得到了明顯的改善,且在9.31 s左右就能達到穩定狀態。 圖6 BP-PID優化前后仿真結果對比圖Fig.6 Comparison of simulation results before and after BP-PID optimization σ/%tr/stp/sts/s常規PID65.643.204.9414.66BPNN-PID28.874.116.1713.75主成份-BP神經網絡-PID44.743.555.169.31 注:σ、tr、tp、ts分別為超調量、上升時間、峰值時間、調節時間(下同)。 該工況仿真方法同工況一,各整定方案下PID參數如表5所示。 表5 工況二各整定方案PID參數Tab.5 The PID parameters of each setting scheme on second working condition 工況二(非額定工況)下各控制方案PID控制仿真圖: 從圖7和表6不難看出,在工況二主成份優化后的BP神經網絡PID控制系統也獲得了較好的控制效果。 圖7 工況二各控制方案仿真曲線Fig.7 Simulation curves of each control scheme of the second working condition σ/%tr/stp/sts/s常規PID60.372.784.5913.12BP-PID6.474.375.849.83主成份-BP神經網絡-PID06.836.836.83 從上面的結果來看,采用主成份優化的BP神經網絡PID控制器對被控系統的控制效果明顯好于常規PID控制、BPNN-PID控制,調節時間(或超調量)明顯縮短(或降低),波動程度明顯改善。 綜上所述,我們將主成份優化后的BP神經網絡PID控制進行了水輪機調節實例仿真試驗,取得了較好的結果。該方法有效地彌補了BP神經網絡算法收斂速度慢的影響,改善了控制系統跟蹤性能,具有一定的實際意義。 □ [1] 袁海鋒.PID控制器參數整定與自整定方法的研究[D]. 南京:南京工業大學,2007. [2] 侯樹文, 王琳琳, 盧家濤,等. BP網絡模糊PID控制在水輪機調速器中的應用[J]. 人民長江, 2008,39(2):79-80. [3] 許永強,劉萬康.基于主成分-BP神經網絡的我國農村居民用電量的預測研究[J].電力學報,2016,(2):162-166. [4] 李旭軍.基于PCA方法的地理系統分析[J].赤峰學院學報(自然科學版),2011,(12):41-43. [5] 何繼愛, 達正花. BP神經網絡PID控制器仿真實現[J]. 蘭州文理學院學報(自然科學版), 2005,19(2):31-34. [6] 陳鐵華,李樹剛.基于神經網絡的水輪機調節系統非線性仿真[J].水電能源科學,2012,30(10):120-123,215. [7] 程遠楚,張江濱.水輪機自動調節[M]. 北京:中國水利水電出版社,2010. [8] 盧禮華,郭永豐,大刀川博之,等.高增益PID控制器實現納米定位[J].光學精密工程,2007,(1):63-68.1.2 主成份-BP神經網絡-PID控制器
1.3 水輪機調速系統的組成及數學模型



2 算例仿真
2.1 工況一實例仿真






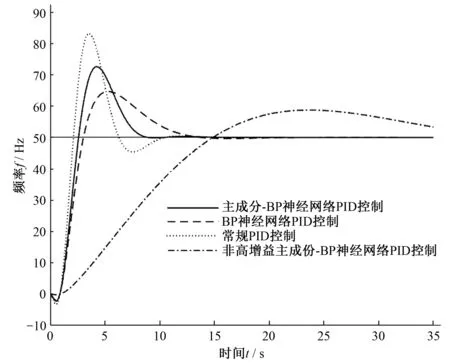

2.2 工況二實例仿真



3 結 語

