風力機葉片氣動性能設計研究

李文浩，余 波，張禮達，崔軍玲

(西華大學能源與動力工程學院，四川 成都 610039)

風力機氣動設計的任務就是利用合理的風輪氣動計算方法來配置合理的葉片參數(如翼型的選擇、翼型的布置、弦長和扭角的分布)，從而達到提高風能利用系數的目的［1］。而我國的風力機葉片氣動設計技術較國外還有一定的差距，因此，開展風力機葉片的氣動設計研究是風力機發展中的重要課題。

在風力機葉片氣動設計中，研究者們往往在設計中把主要翼型沿葉片展向位置事先固定，再進行氣動設計［2～6］。由于主要翼型沿葉片展向的位置事先固定，而這樣就可能造成所設計的風力機葉片氣動性能達不到最優，故把葉片弦長、扭角和主要翼型沿展向的分布作為控制變量，基于遺傳算法以風能利用系數最大化為目標，開展風力機葉片氣動性能設計研究。

1 基于遺傳算法的葉片氣動設計程序

根據經典風力機葉片氣動設計理論動量—葉素理論［7］，考慮葉片損失(葉根損失、葉尖損失)、推力系數修正和葉片厚度、寬度對葉素攻角的改變，編寫出風力機氣動性能計算程序。把氣動性能計算程序作為遺傳算法的個體評價函數，以風能利用系數最大化為目標，在MATLAB平臺上編寫了基于遺傳算法的風力機葉片氣動設計程序。基于遺傳算法的風力機葉片氣動性能設計程序流程如圖1所示。

1.1 動量—葉素理論

氣體軸向誘導因子a和周向誘導因子a'可通過迭代求得，迭代方程為

式中，B為葉片數;c為弦長;Cl為升力系數;Cd為阻力系數;r為展向位置;φ為入流角。

1.2 普朗特損失因子

Prandtl考慮到葉尖和葉根損失，對動量—葉素理論做了修正，定義了葉尖和葉根的損失系數。

式中，R為葉片半徑;R0為輪轂半徑。

1.3 推力修正

在軸向誘導因子a＞0.5時，動量理論預測的尾流中的氣流將會反向，這種情況在實際中是不可能發生的，必須用以下經驗公式代替

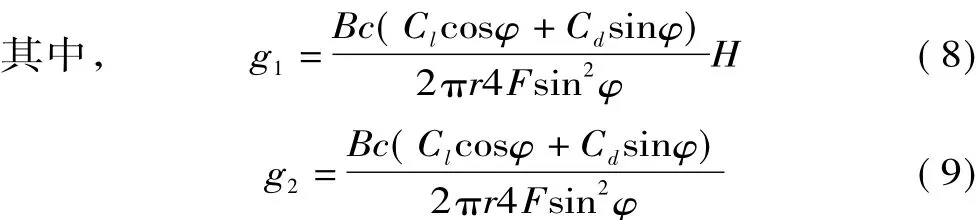
當 a≤0.353 9，H=1.0時;a＞0.353 9時，

1.4 葉片厚度和寬度對攻角的影響

葉柵理論研究葉片厚度和寬度的影響導致的攻角變化，攻角改變量可由下式表述［8～9］

式中，Δα1為葉片寬度對氣流方向的影響引起的攻角改變量;Δα2為葉片厚度對氣流方向的影響引起的攻角改變量;tmax為翼型的最大厚度;V1為風速;Ω為角速度。

1.5 葉片性能計算程序流程

風力機葉片氣動性能計算程序如下:

(1)將風力機葉片分成若干等分，確定每個葉素上的翼型外形以及氣動特性。

式中β為扭角。

(5)以步驟(3)求得的合速度對應的雷諾數調用翼型氣動特性數據，考慮葉片損失、推力修正和葉片厚度、寬度對攻角的影響，根據公式(3)～(12)，在允許誤差范圍內通過迭代確定軸向和周向誘導因子。

(6)迭代求得誘導因子對應的合速度后，雷諾數也相應的發生變化，代入該雷諾數下的翼型氣動數據，在允許雷諾數誤差下重復步驟(2)～(5)。

(7)求得所有截面的推力、扭矩數據，通過積分求得整個葉片的推力、功率、轉矩、風能利用系數等氣動參數。

2 算例

2.1 風力機基本參數的選取

風力機額定功率Pe為1.5 MW，風力機額定轉速n為19.5 r/m，額定風速Ve為10.3 m/s，電機效率η1取值為0.95，傳動效率η2取值為0.95，空氣密度ρ取值為1.205 kg/m3，假設風能利用系數為0.48，風輪直徑D可由下式求得

風輪半徑R=40.3 m。

高速風力機的尖速比一般取值在6～8之間，設計尖速比可由下式求得

2.2 過渡翼型的處理

采用翼型數據沿厚度的線性平均化方法來對翼型數據進行插值處理。

過渡翼型數據計算方法為［10］

式中，t為過渡翼型的相對厚度，t1、t2分別為過渡翼型兩側設計翼型相對厚度，且t1＜t2;y為過渡翼型的坐標數據或氣動特性數據，y1、y2分別為過渡翼型兩側設計翼型的坐標數據或者氣動特性數據。

2.3 控制變量的選擇

弦長、扭角控制曲線采用具有局部修改能力且靈活度較好的準均勻二次B樣條曲線來進行控制［11］。根據弦長、扭角曲線的特點，選擇7個控制點來控制曲線，以這7個控制頂點的橫坐標和縱坐標為變量。B樣條基函數的節點向量選擇為［1.3 10 20 25 35 40.3］，則B樣條基函數曲線如圖所示，曲線控制方程為

圖2 B樣條基函數曲線

式中，P(x0，y0) ～ P(x6，y6) 為控制點;N0，3～ N6，3為B樣條基函數，如圖2所示。其中，弦長、扭角曲線首末端點的橫坐標分別確定為x0=1.3和x6=40.3，弦長曲線控制頂點坐標控制范圍為:y0=［1.5 1.8］;x1=［3 5］;y1=［1.5 1.8］;x2=［5 10］;y2=［1.5 2.3］;x3=［15 20］;y3=［1.5 2］;x4=［35 40］;y4=［1.5 2］;x5=［38 40.2］;y5=［1.5 2］;y6=［0 1］; 扭角曲線控制頂點坐標控制范圍為:y0=［5 10］;x1=［2 10］;y1=［5 15］;x2=［5 15］;y2=［10 30］;x3=［5 20］;y3=［5 25］;x4=［15 35］;y4=［0 15］;x5=［35 40］;y5=［－10 10］;y6=［0 10］。

在NREL S翼型族［12］中，S83X系列具有相對良好的氣動特性，故在葉根處選擇厚度為24%的S818翼型，在葉中部位布置厚度分別為21%、18%的S830翼型和S831翼型，在葉尖部位布置相對厚度為15%的S832翼型。故主要翼型位置變量有3個，翼型位置按占葉片展向百分比來表示，控制范圍為:S818［0.4 0.58］;S830［0.6 0.78］;S831［0.780.95］，所有變量共計27個。

2.4 遺傳算法參數選取

根據各編碼、選擇、交叉、變異操作的優缺點［13］以及風力機葉片氣動設計的特點，選用格雷碼作為編碼方式，選用隨機歷遍抽樣以0.9的概率進行選擇重組，選用單點交叉以0.7的概率進行交叉操作，染色體中每個元素的變異概率近似為0.5。確定種群數量為80，遺傳代數為250代。

3 結果分析

以風能利用系數最大化為目標，在運行基于遺傳算法的風力機葉片設計程序后，在最大遺傳代數250代內，風能利用系數逐漸收斂于一個最優解。如下圖3所示，在50代以內風能利用系數很低，呈逐漸上升趨勢;50代以后，風能利用系數上升趨勢明顯減緩，直至250代，逐漸收斂于0.480 7。

圖3 種群解的變化

風力機葉片氣動性能設計程序得到的軸向誘導因子α和周向誘導因子α'沿展向的分布分別如圖4、5所示。由圖4可知，軸向誘導因子α在葉根處較小，沿葉片展向逐漸增加至理想值0.33左右。這是由于葉根處厚度較大，對來流形成了堵塞，對風能的利用較小;在葉片中段部位，軸向誘導因子α大致在理想值0.33左右;在葉尖處，軸向誘導因子a增大，對風能的利用較大。由圖5可知，由于葉根部氣流阻塞，周向誘導因子在葉根處較大，沿葉片展向位置逐漸降低，并接近于0。

圖4 軸向誘導因子隨葉片展向變化曲線

圖5 周向誘導因子對葉片展向變化曲線

對所設計葉片的總體氣動性能進行評估，計算其在設計狀態和非設計狀態下的不同葉尖速比的風能利用系數CP。根據尖速比分別為3、4、5、6、7、8、9、10、11、12、13時，葉片風能利用系 數 分 別 為 0.134、0.213、0.318、0.405、0.454、0.479、0.481、0.471、0.448、0.417、0.378，圖6給出分別為風能利用系數隨尖速比的變化曲線。

圖6 風能利用系數Cp隨葉尖速比λ變化曲線

由圖6所示，從啟動風速開始，隨著尖速比增加，風能利用系數逐漸增加，在達到設計尖速比8時達到最大值，而后逐漸減小，設計尖速比與曲線中最大風能利用系數對應的尖速比基本相等，驗證了所設計葉片的合理性。

設計程序運算結束后求得風能利用系數為0.480 7的風力機葉片弦長、扭角參數如表1所示，弦長、扭角沿葉片展向分布分別如圖7、8所示。4結論

表1 弦長、扭角沿葉片展向分布

圖7 風力機葉片弦長分布

圖8 風力機葉片扭角分布

開展了以弦長、扭角曲線和主要翼型安放位置為變量，以風能利用系數最大化為目標的風力機葉片氣動性能遺傳算法設計研究。運用7個頂點控制的準均勻二次B樣條曲線控制弦長、扭角曲線的方法比之Bezier曲線控制更具靈活性以及增加了局部修改的能力，該方法應用于風力機弦長、扭角曲線的控制更具優勢。

在給定變量范圍內，最終利用程序成功搜索到了在風力機設計參數下風能利用系數達到0.480 7的風力機葉片，計算了在設計狀態和非設計狀態下的不同葉尖速比的風能利用系數Cp，驗證了設計工況下的風力機葉片性能為最佳。所使用的以弦長、扭角曲線和主要翼型分布位置為變量的風力機葉片氣動性能遺傳算法設計方法，可作為風力機葉片設計的參考方法。

［1］賀德馨．風工程與工業空氣動力學［M］．北京:國防工業出版社，1979．

［2］戴巨川，趙尚紅，尹喜云，等．大型風力機葉片氣動外形及其運行特性設計優化［J］．機械工程學報，2015，51(17):138-144．

［3］董禮，廖明夫，井延偉．風力機葉片氣動設計及偏載計算［J］．太陽能學報．2009，30(1):122-128．

［4］黃之龍，劉沛清，趙萬里．某兆瓦級水平軸風力機葉片氣動設計和性能評估［J］．電網與清潔能源．2010，26(1):68-72．

［5］張釗．大型水平軸風力機葉片氣動優化設計及氣動載荷分析［D］．蘭州:蘭州理工大學，2013．

［6］汪泉．風力機葉片氣動外形與結構的參數化耦合設計理論研究［D］．重慶:重慶大學，2013．

［7］蔡新．風力發電機葉片［M］．北京:中國水利水電出版社，2014．

［8］趙萬里．大型風力機氣動設計及流動控制研究［M］．北京:中國水利水電出版社．2001．

［9］李軍向．大型風機葉片氣動性能計算與結構設計研究［D］．武漢:武漢理工大學，2008．

［10］廖明夫，宋文萍，王四季，等．風力機設計理論與結構動力學［M］．西安:西北工業大學出版社，2014．

［11］任洪海．計算機圖形學理論與算法基礎［M］．沈陽:遼寧科學技術出版社，2012．

［12］SOMERS D M．The S830，S831，and S832 airfoils November 2001-November 2002［R］．Washington:National Renewable Energy Lab，2005．

［13］雷英杰等．MATLAB遺傳算法工具箱及應用［M］．西安:西安電子科技大學出版社，2014．