一類二維非自治離散系統中的復雜簇發振蕩結構1)

陳振陽 韓修靜畢勤勝

(江蘇大學土木工程與力學學院，江蘇鎮江212013)

一類二維非自治離散系統中的復雜簇發振蕩結構1)

陳振陽 韓修靜2)畢勤勝

(江蘇大學土木工程與力學學院，江蘇鎮江212013)

簇發振蕩是多時間尺度系統復雜動力學行為的典型代表，簇發振蕩的動力學機制與分類問題是簇發研究的重要問題之一，但當前學者們所揭示的簇發振蕩的結構大多較為簡單.研究以非自治離散Duffing系統為例，探討具有復雜分岔結構的新型簇發振蕩模式,并將其分為兩大類，一類經由Fold分岔所誘發的對稱式簇發，另一類經由延遲倍周期分岔所誘發的非對稱式簇發.快子系統的分岔表現為典型的含有兩個Fold分岔點的S形不動點曲線，其上、下穩定支可經由倍周期(即Flip)分岔通向混沌.當非自治項(即慢變量)穿越Fold分岔點時，系統的軌線可以向上、下穩定支的各種吸引子(例如，周期軌道和混沌)進行轉遷，因此得到了經由Fold分岔所誘發的各種對稱式簇發；而當非自治項無法穿越Fold分岔點，但可以穿越Flip分岔點時，系統產生了延遲Flip分岔現象.基于此，得到了經由延遲Flip分岔所誘發的各種非對稱簇發.特別地，文中所報道的簇發振蕩模式展現出復雜的反向Flip分岔結構.研究結果表明，這與非自治項緩慢地反向穿越快子系統的Flip分岔點有關.研究結果豐富了離散系統簇發的動力學機理和分類.

離散Duffing系統，復雜的簇發振蕩模式，延遲Flip分岔，反向Flip分岔結構

引言

諸如神經元的簇放電活動[1-3]、化工生產中液體的流動特性[4]、反應物的反應速率[5-6]和濃度[7]的變化、湍流的脈動分析[8]、生物代謝過程中的變構效應[9]、環境因素對農作物生長的影響[10]等實際問題，很難用單一時間尺度的動力學模型來描述，必須采用含多個時間尺度的耦合模型加以刻畫.與一般的非線性系統相比，多時間尺度耦合系統具有獨特的復雜動力學行為，比如所謂的簇發振蕩(bursting oscillations).簇發振蕩的基本單元被稱為振蕩簇，所謂振蕩簇，即去極化波形上的一系列動作電位[11]，故對簇發振蕩而言，其特征在于在每一演化周期中，小幅振蕩與大幅振蕩的交替出現.現有的研究表明，簇發振蕩通常是不同時間尺度耦合作用的產物[12]，而其中的耦合作用機制可用Rinzel的快慢分析法[13]加以解釋.該方法隨后被Izhikevich[1]用在簇發的分類研究中，在理論上極大拓展了不同時間尺度之間各種可能的耦合作用機制.基于Rinzel的快慢分析和Izhikevich的分類工作，國內外學者從理論[14-15]、數值[3,16]和實驗[3,17]等方面對不同時間尺度的耦合系統，尤其是其中的多時間尺度簇發振蕩模式，做了系統、深入的研究，取得了豐碩的成果.

近年來，基于離散系統的多時間尺度耦合效應逐漸受到了學者們的廣泛關注.Channell等[18]指出，采用Poincar′e映射可將連續時間系統約化為一維Poincar′e映射；然后，通過對Poincar′e映射的分析來揭示原系統中的簇發振蕩的動力學特性和轉遷機制.Izhikevich等[19]指出，用離散映射去實現連續系統中的簇發振蕩在理論上是可行的.隨后，Courbage等[20]提出了一個二維映射，以此再現了真實神經系統中包括簇發在內的各種放電模式.而Maslennikov等[21-22]的研究進一步表明，離散映射是研究單個神經元乃至復雜神經網絡的有效工具.基于前人的研究工作，特別是Rinzel的快慢分析法，文獻[19]利用分岔理論系統地探討了一維和二維離散系統中各種可能的簇發振蕩模式，并對它們進行了分類.

然而，需要指出的是，到目前為止，大部分已報道的離散簇發振蕩模式均較為簡單.這主要表現在兩個方面，一是與連續的尖峰(repetitive spiking)相對應的激發態的分岔模式較為簡單.對于連續尖峰內部仍有分岔的情形，相關文獻少有涉及；二是所報道的激發態通常是周期軌道,對于激發態是非周期(例如，混沌)的情形，鮮有報道.基于此，考慮受擾動的Duffing映射[23]

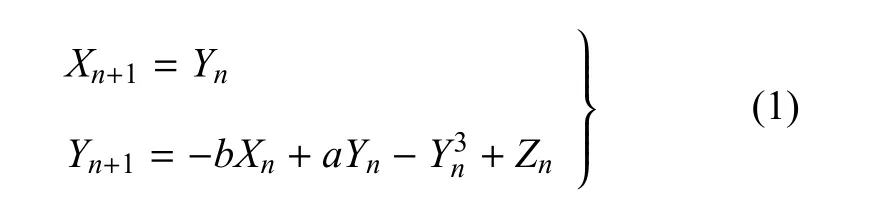
其中a,b是實參數,Zn是慢變的擾動項.為了便于分析，假設Zn是周期擾動，即Zn=Fcos(ωn),其中F為擾動項的振幅，而頻率ω遠低于系統的固有頻率ω0，即ω?ω0.本文以系統(1)為例，旨在探討復雜的簇發振蕩模式及其誘發機制.說明系統在由激發態向沉寂態轉遷之前可能會發生多次分岔，因此簇發振蕩可以呈現出復雜的分岔結構.此外，激發態不僅可以是周期振蕩，也可以是混沌態，因此簇發振蕩可以展現復雜的振蕩形式，即在簇發振蕩中能夠觀測到混沌式的振動簇.

1 快子系統的分岔分析

由于擾動項的頻率遠遠低于系統的固有頻率，因此在較慢的尺度上演化，而未受擾的Duffing映射則在相對較快的尺度上演化.顯然，受擾系統(1)是一個典型的快慢系統，它由快、慢子系統耦合而成.快子系統由如下映射給出

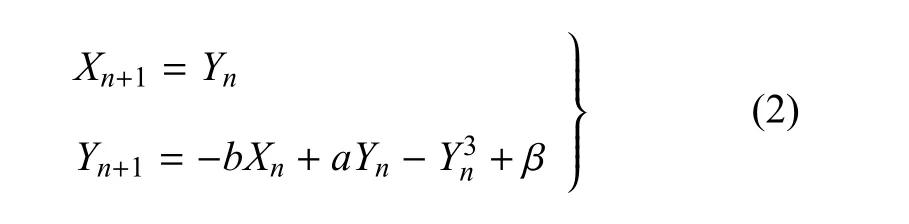
其中，β=Zn是控制參數；而慢子系統(慢變量)則由Zn=Fcos(ωn)刻畫.

一般說來，簇發振蕩因軌線在快子系統的吸引子之間相互轉遷而產生，這種轉遷是由慢變量穿越快子系統的分岔點加以調控[124].因此，快子系統的穩定性和分岔行為對簇發振蕩的產生起決定性作用.基于此，本部分探討快子系統(2)的穩定性和分岔行為.

為了直觀地了解系統的分岔行為，圖1給出了快子系統關于參數β的單參數分岔圖，其中參數b固定在b=0.35.圖中FB±代表不動點F±的Fold分岔;PD±n-2n(n=1,2)代表上、下半支周期n到周期2n的Flip分岔.如圖所示，當β從0出發穿越FB-時，吸引子F-與排斥子F0碰撞、消失，即發生了Fold分岔.隨著β的不斷增大，吸引子F+因倍周期(即Flip)分岔逐漸演化為混沌,而當β從0出發不斷減小時，可以觀測到類似的動力學演化行為.

為了進一步揭示系統的分岔行為，圖2給出了快子系統在平面(β,b)上的兩參數分岔集，其中各分岔曲線的含義與圖1相同.注意到快子系統具有對稱性：(Xn,Yn,β)→(-Xn,-Yn,-β)，即快子系統的穩定性和分岔行為關于β=0對稱.因此，如果β=β1時，快子系統存在某種穩定性或分岔行為，那么當β=-β1時，快子系統必然存在著同樣的穩定性或分岔行為(見圖1和圖2).

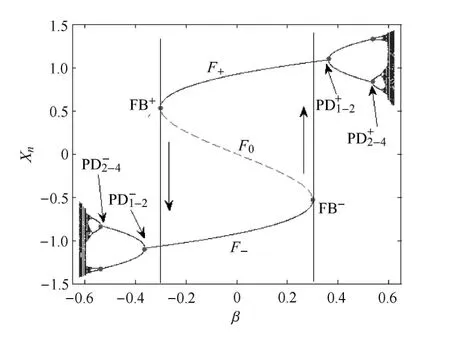
圖1 快子系統關于單參數β的分岔圖Fig.1 One parameter bifurcation diagram of the fast sub-system with respect to β

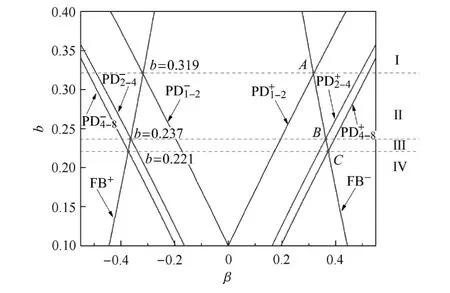
圖2 快子系統在(β,b)平面上的分岔集Fig.2 Bifurcation set of the fast system on the plane(β,b)

如圖 2所示，A,B,C分別是 Fold分岔曲線和倍周期分岔曲線的交點，它們的縱坐標依次是bA=0.319,bB=0.237,bC=0.221.過點A,B,C作三條水平線，它們將參數平面劃分為I,II,III,IV四個區域，對應著快子系統不同的動力學行為.

易知，圖1所示的分岔圖是區域I中分岔行為的典型代表，其特征是在Fold點附近可以觀測到由兩個不動點吸引子構成的雙穩態.因此，Fold分岔將誘發從一個不動點吸引子(如F+)到另一個不動點吸引子(如F-)的轉遷.然而，如圖2所示，當參數b不斷減小時，Fold分岔值逐漸增大，而各Flip分岔值不斷減小.特別地，當Fold分岔曲線落在兩條Flip分岔曲線之間時，Fold點附近的雙穩態會發生定性的變化.因此，由Fold分岔所誘發的轉遷必然也會隨之定性地改變.基于此，接下來我們探討幾類典型的轉遷模式.

情形1：從不動點向周期2吸引子的轉遷.這種轉遷模式對應著參數b屬于區域II時的情形.圖3(a)給出了區域II中典型的分岔行為.可見，Fold分岔點附近的雙穩態已經發生了定性的變化，即不動點與周期2軌道共存.因此，Fold分岔誘發了系統從不動點吸引子向周期2軌道的轉遷.

情形2：從不動點向周期4吸引子的轉遷.當參數b屬于區域III時，可以得到另一種不同的轉遷模式，即由Fold分岔所誘發的從不動點吸引子向周期4軌道的轉遷.圖3(b)給出了區域III中典型的分岔圖.由于不動點吸引子與周期4軌道在Fold點附近共存，因此Fold分岔誘發了從不動點向周期4吸引子的轉遷.由于不動點吸引子經由Flip分岔通向混沌，因此在的左側區域以及的右側區域存在著間距越來越狹窄的無數條Flip分岔曲線.這些Flip曲線與周期2n(n≥3)等具有較高周期的軌道相對應，并逐漸將周期軌道以Flip分岔的方式引向混沌.因此，隨著參數b進入IV區并不斷減小，可以得到從不動點向高周期軌道2n(n≥3)甚至是混沌吸引子的轉遷.

情形3：從不動點向周期8吸引子的轉遷.當b=0.22時，圖3(c)給出了區域IV中的一種典型的分岔轉遷行為.可見，在Fold分岔點附近，不動點吸引子與周期8吸引子共存，因此由Fold分岔誘發了從不動點向周期8軌道的轉遷.

圖3 映射(2)關于參數β的典型單參數分岔圖Fig.3 Typical one parameter bifurcation diagrams of the map(2)with respect to β

情形4：從不動點向混沌吸引子的轉遷.在區域IV內繼續調整b的值，可得如圖3(d)所示的向混沌吸引子轉遷的模式.在Fold分岔點附近，系統處于不動點吸引子與混沌吸引子共存的雙穩態，進而會出現由Fold分岔所誘發的向混沌吸引子的轉遷.

2 對稱式簇發

前面已經探討了快子系統的分岔行為，分析表明：由于在Fold點附近不動點吸引子可與多種周期軌道甚至混沌共存，因此Fold分岔可以誘發從不動點向不同類型吸引子的轉遷.基于此，本部分進一步探討與這些轉遷相關的各種簇發振蕩模式.

2.1 對稱式“Fold/反向Flip”簇發

當b位于II區時，系統能夠產生對稱式“Fold/反向Flip”簇發.不失一般性，考慮b=0.25的情形來解釋這種簇發振蕩的產生機理.注意到當Zn=Fcos(ωn)處于 βFB+與βFB-之間時，系統處于雙穩態，因此要實現軌線在不同吸引子間的轉遷,就必須使Zn能夠穿越βFB±.由數值計算可知，βFB-=0.356，故這里選取Zn=0.38cos(ωn)，其振幅略大于βFB-.圖4(a)給出了系統在該參數條件下的簇發行為.為進一步闡明系統軌線隨慢變量的變化趨勢，在此將Zn視為廣義變量,給出相應的轉化相圖[25-26],并將其與分岔圖疊加，如圖4(b)所示.

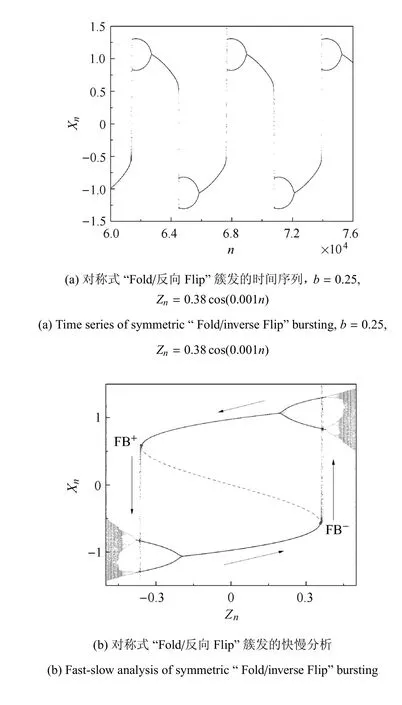
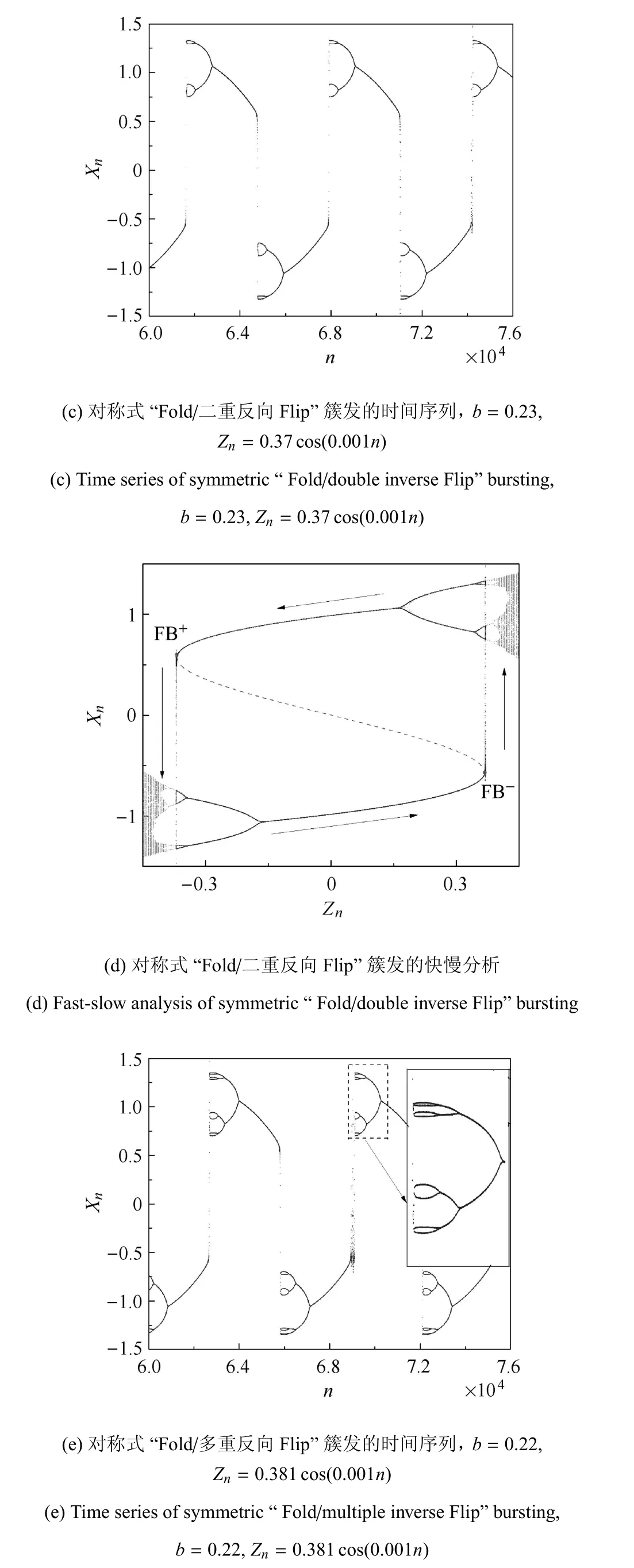
圖4 不同的對稱簇發Fig.4 Dif f erent symmetric bursting

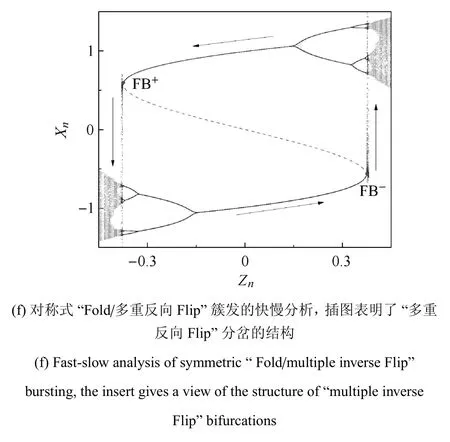
圖4 不同的對稱簇發(續)Fig.4 Dif f erent symmetric bursting(continued)

從圖4(b)中可以看出，當Zn從0出發逐漸增大至βFB-時,原本處于下半支的軌線會由于Fold分岔而轉遷到上半支的周期2吸引子，從而使系統進入激發態.Zn在到達最大值0.38后，開始逐漸減小，并“反向”地穿過使得激發態終止，系統進入沉寂態F+;隨著Zn繼續減小，直至越過FB+，雙穩態再次被破壞，軌線躍遷到下半支的周期2吸引子;在此之后，系統通過與前述過程相似的方式再次回到沉寂態，并進入下一個周期的演化.此過程中，系統由沉寂態進入激發態是通過Fold分岔，而激發態的終止則是通過反向Flip分岔.根據文獻[1]中的分類方法，同時考慮到對稱性，這種簇發行為可以歸類為對稱式“Fold/反向Flip”簇發.

2.2 對稱式“Fold/二重反向Flip”簇發

當b位于III區時，可以得到另一種不同的簇發形式.考慮b=0.23的情況，此時βFB-=0.369.選取Zn=0.37cos(ωn),顯然Fold分岔將會發生，這預示著簇發將會出現.

圖4(c)給出了含二重反向(double inverse)Flip分岔結構的簇發模式，相應的轉化相圖為圖4(d).當Zn越過FB-后，軌線會躍遷到周期4吸引子，該吸引子隨后經過二重反向Flip分岔演變為F+.緊接著系統經歷與之對稱的演變，并進入下一周期.按之前的分類方法，這種激發態為周期4軌道的簇發模式可命名為對稱式“Fold/二重反向Flip”簇發.

2.3 對稱式“Fold/多重反向Flip”簇發

由備注2知，若b位于IV區,系統可產生激發態為周期8等高周期軌道乃至混沌的簇發振蕩.如取b=0.22,F=0.381,通過數值模擬可發現，系統在通過Fold分岔由沉寂態轉遷到周期8軌道后，經由多重反向Flip分岔演變到沉寂態.對該簇發振蕩模式，可將其稱作對稱式“Fold/多重反向Flip”簇發,見圖4(e)和圖4(f).

2.4 對稱式“Fold/級聯反向Flip”簇發

根據前面所做的分析，在區域IV中繼續調整b的值，可以得到激發態為混沌乃至周期窗口的簇發模式.圖5給出了混沌激發態的簇發振蕩模式，其中b=0.215，F=0.4，快子系統分岔行如圖3(d).當Zn越過Fold分岔點后，系統轉遷到混沌狀態，隨后系統又經過一系列反向Flip分岔回到沉寂態，故可將其命名為對稱式“Fold/級聯反向Flip”簇發.

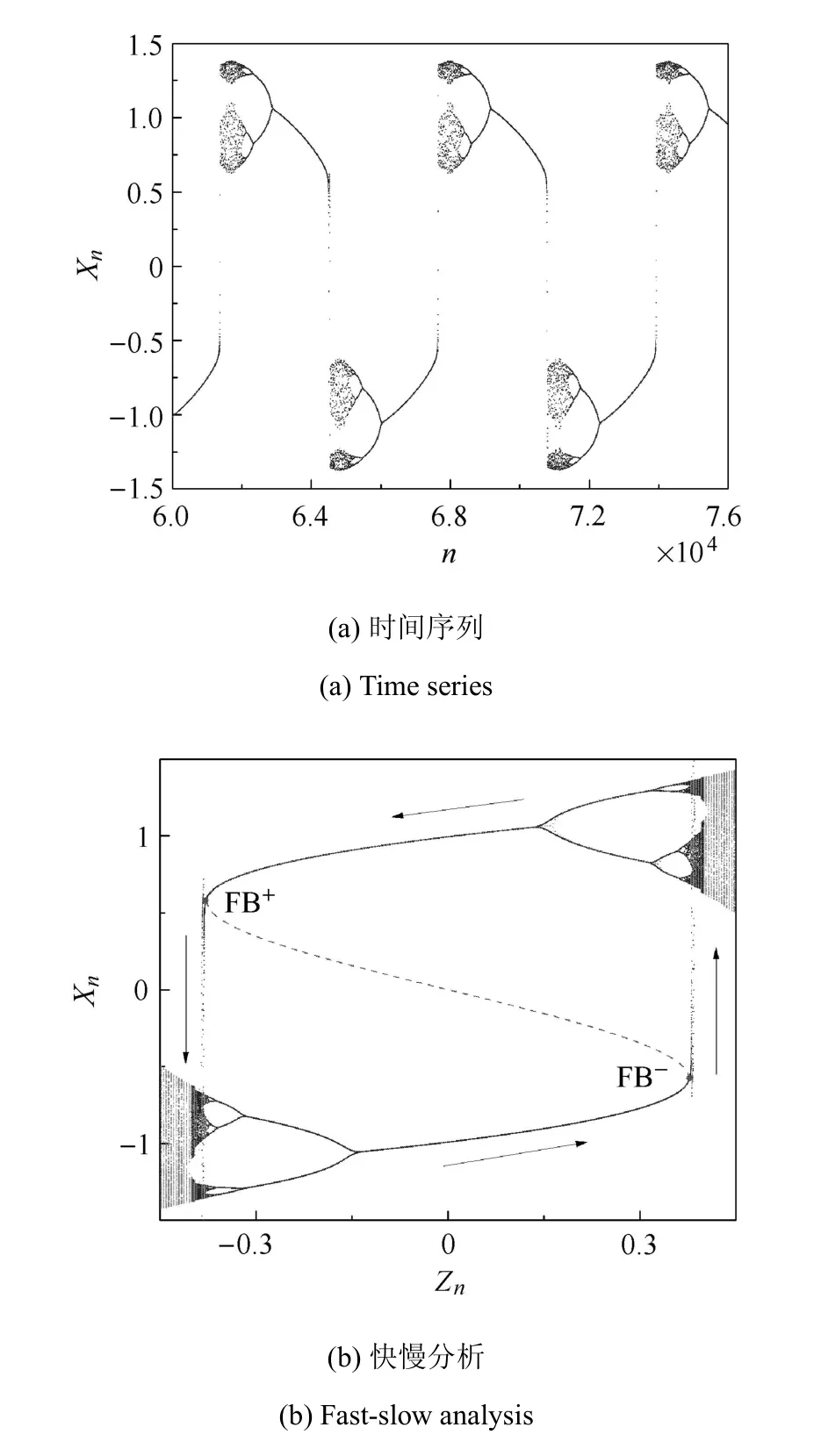
圖5 對稱式“Fold/級聯反向Flip”簇發,b=0.215,Zn=0.4cos(0.001n)Fig.5 Symmetric“Fold/a cascade of inverse Flip”bursting,b=0.215,Zn=0.4cos(0.001n)

進一步的數值模擬顯示，在快子系統分岔圖中,存在著一些使系統展現出周期性的孤立區間，將混沌區分割成若干段，這意味著可能存在與不動點共存的周期窗口.例如，取a=1.975,b=0,F=0.38時,快子系統的單參數分岔圖為圖6(a),簇發行為則如圖6(b)所示.當Zn越過FB±后，系統從沉寂態轉遷到周期3軌道，并迅速進入混沌，之后又通過一系列反向Flip分岔演變為沉寂態，從而產生一種分岔結構不同于圖5(a)的混沌簇發模式.

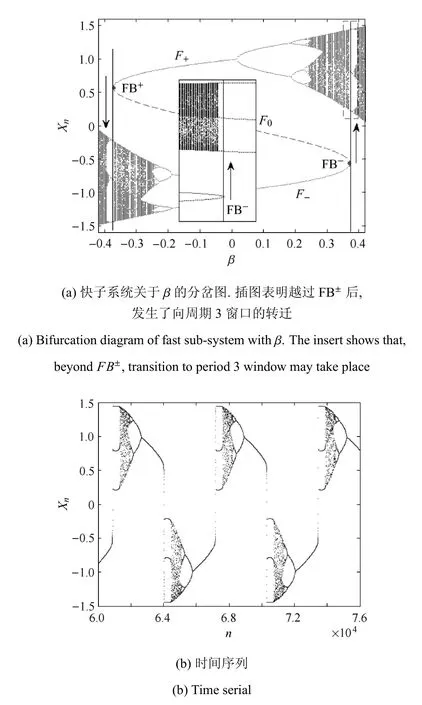
圖6 另一種混沌簇發,a=1.975,b=0,Zn=0.38cos(0.001n)Fig.6 Another chaotic bursting,wherea=1.975,b=0,Zn=0.38cos(0.001n)

3 非對稱式簇發

前面探討了由Fold分岔所誘發的幾種復雜簇發振蕩模式及其動力學機理，這些簇發振蕩模式的產生離不開慢變量對Fold分岔點的周期穿越，即要求慢變量具有足夠大的振幅.本文接下來的內容，將探討慢變量振幅相對較小，即慢變量無法穿越Fold分岔點時，系統可能存在的簇發振蕩模式.

3.1 “延遲Flip/反向Flip”簇發

圖7給出了b=0.2時,快子系統關于β的單參數分岔圖，其中Fold分岔值和各Flip分岔值分別是我們以此為例，探討簇發振蕩模式的產生.由于慢變量無法穿越Fold分岔點，因此軌線無法在快子系統的上、下穩定支之間來回轉遷，即軌線必然會沿某一穩定支(可以是上半支，也可是下半支)，這由軌線的初值決定演化[27].

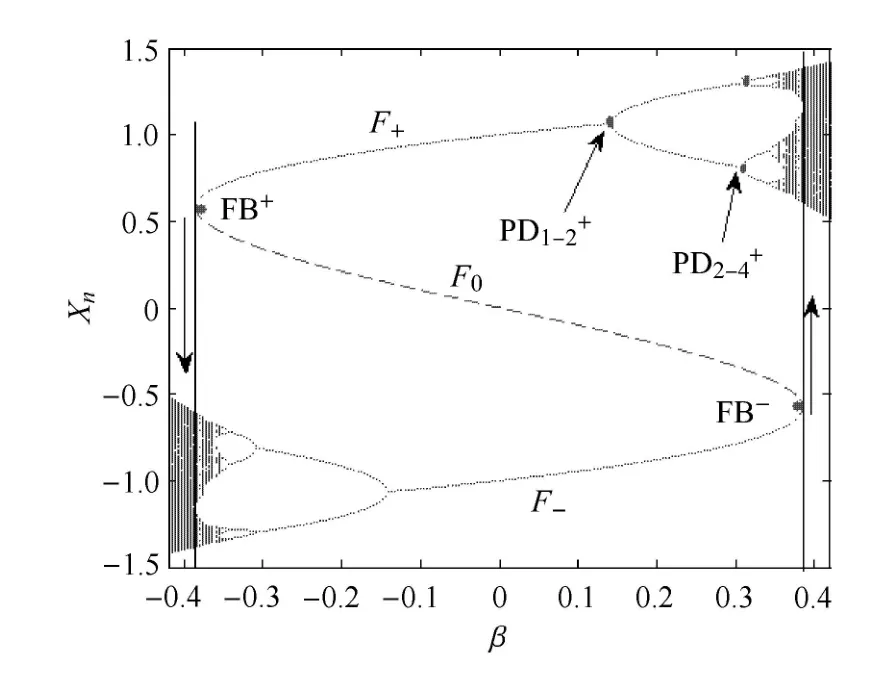
圖7 b=0.2時快子系統關于β的分岔圖Fig.7 Bifurcation diagram of fast subsystem with β forb=0.2

圖8(a)給出了Zn=0.27cos(0.001n)時系統的一種簇發振蕩模式.為了揭示其中的動力學機制，圖8(b)進一步給出了該簇發的轉換相圖與分岔圖的疊加.由圖8(b)可知，當慢變量不斷增加、穿越Flip分岔點時，系統出現了有趣的延遲分岔現象.延遲分岔，又稱為慢過效應(slow passage ef f ect)或記憶效應[28-29](memory ef f ect)，是吸引子的一種延遲失穩現象[30-31]，即當吸引子失穩變成排斥子時，系統的軌線繼續在排斥子上停留了一段時間，然后再離開排斥子的現象.由于延遲的作用，該參數組合下出現了排斥子F+與周期2軌道間的滯后.因此，當延遲結束時，軌線得以迅速向該周期2吸引子轉遷，從而導致激發態的出現.

當Zn不斷減小，“反向”越過Flip分岔點時，數值計算表明：系統在Zn=0.126處由周期2振蕩進入沉寂態.將其與Flip分岔值相比，盡管仍能觀察到一定的延遲，但相應延遲量明顯小于“正向”通過時的情形.因此，這里只考慮“正向”穿越時的延遲行為，而對“反向”的延遲忽略不計.考慮到系統因延遲Flip分岔從沉寂態進入激發態，隨后又由反向Flip分岔從激發態返回沉寂態，故可以將這種簇發振蕩模式命名為“延遲Flip/反向Flip”簇發.

圖8 “延遲Flip/反向Flip”簇發，b=0.2,Zn=0.27cos(0.001n)Fig.8“Delayed F lip/inverse Flip”bursting,b=0.2,Zn=0.27cos(0.001n)

我們已經看到，延遲 Flip分岔可以引起系統從排斥子向吸引子的災難性轉遷(catastrophic transition)，由此得到了由延遲Flip分岔誘發的簇發振蕩.接下來，我們簡要地分析由延遲Flip分岔誘發的其它幾類典型的簇發振蕩模式，它們與慢變量穿越Flip分岔點以及混沌區域有關.

3.2 “雙重延遲Flip/雙重反向Flip”簇發

當F=0.34時，系統可產生“雙重延遲Flip/雙重反向Flip”式簇發.在Zn越過之后，延遲效應使得軌線繼續停留在不動點上，直至軌線才迅速地轉遷到周期2軌道.隨后，在Zn=0.337處,軌線離開已經失穩的周期2軌道，躍遷到周期4軌道.當Zn達到最大值后，通過雙重反向Flip分岔，系統又回到沉寂態，并進入下一周期，數值模擬結果如圖9.

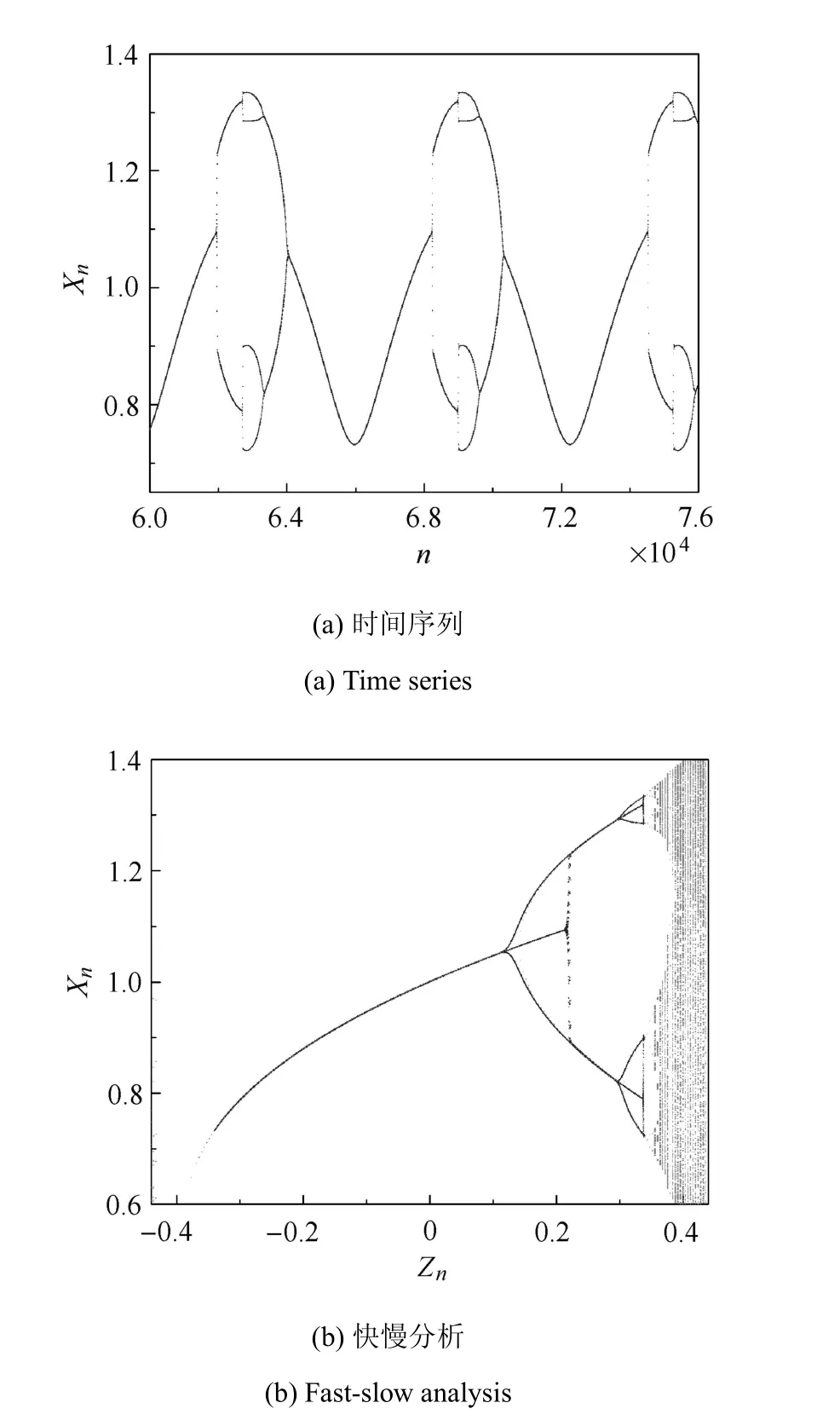
圖9 “雙重延遲Flip/雙重反向Flip”簇發,b=0.2,Zn=0.34cos(0.001n)Fig.9“Delayed double Flip/double inverse Flip”bursting,b=0.2,Zn=0.34cos(0.001n)

3.3 “多重延遲Flip/多重反向Flip”簇發

如圖10，取F=0.35，系統可產生“多重延遲Flip/多重反向Flip”形式的簇發.分岔延遲使得軌線在Zn=0.219處離開不動點，突然轉遷并一直保持在周期2軌道上.直到Zn=0.343時，延遲效應使系統離開已經失穩的周期2軌道，直接躍遷到周期8.當Zn到達最大值后，激發態經由多重反向Flip分岔逐級演變為沉寂態，隨后系統進入下一周期.

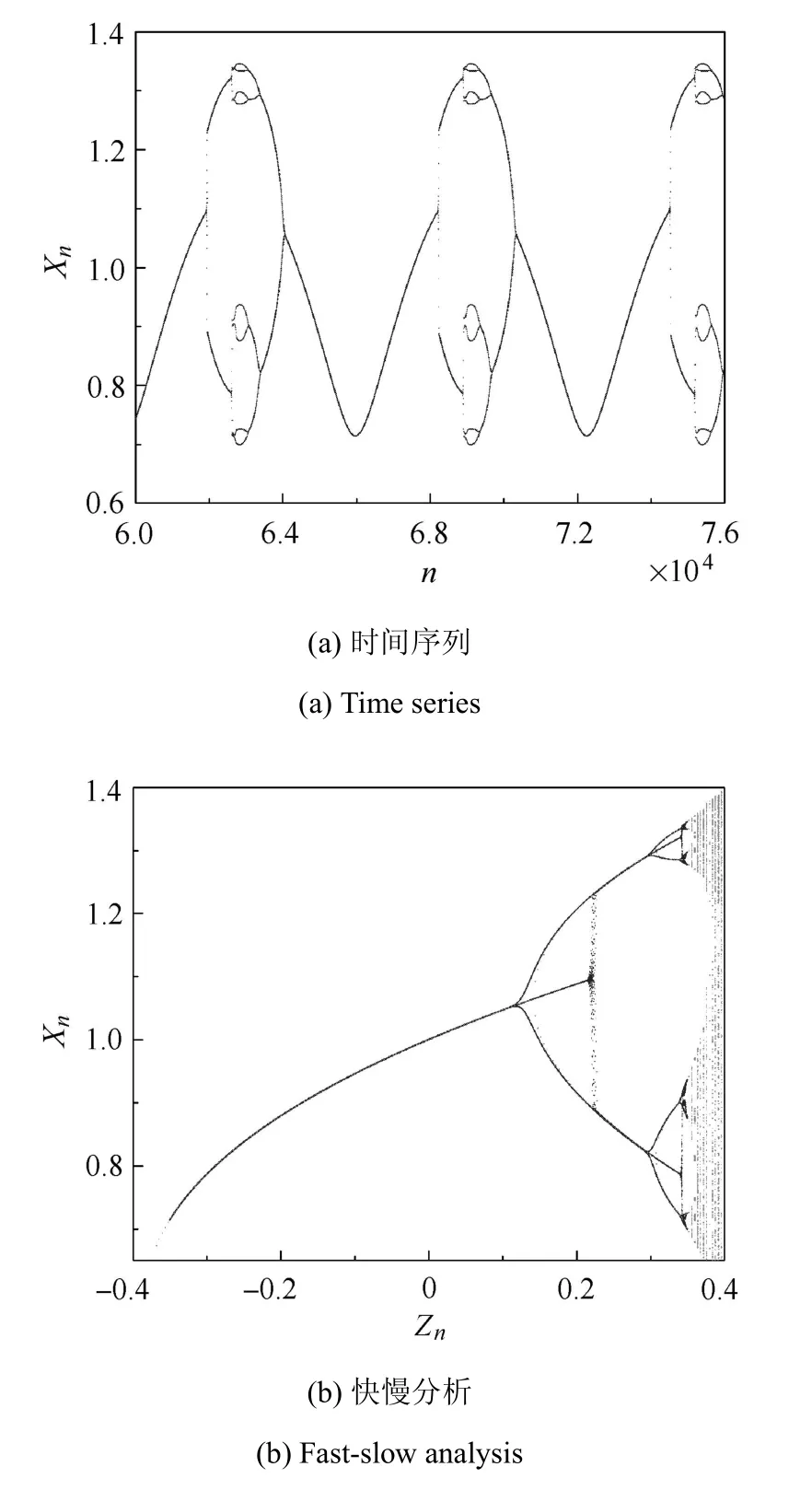
圖10 “多重延遲Flip/多重反向Flip”簇發,b=0.2,Zn=0.35cos(0.001n)Fig.10“Delayed multiple Flip/inverse multiple Flip”bursting,b=0.2,Zn=0.35cos(0.001n)

3.4 “級聯延遲Flip/級聯反向Flip”簇發

當F=0.38時，軌線先在Zn=0.222處轉遷到周期2，隨后出現的第二次分岔延遲則使系統在Zn=0.351處直接進入混沌態.隨著Zn到達最大值，系統又通過一系列反向Flip分岔回到沉寂態，進而進入下一周期，數值模擬如圖11所示.依據前面所采用的分類方法，將其稱為“級聯延遲Flip/級聯反向Flip”簇發.

4 結論

圖11 “級聯延遲Flip/級聯反向Flip”簇發,b=0.2,Zn=0.38cos(0.001n)Fig.11“A cascade of delayed Flip/a cascade of inverse Flip”bursting,b=0.2,Zn=0.38cos(0.001n)

本文以離散Duffing系統為例，探討了由于慢變激勵的存在而誘發的具有復雜分岔結構的簇發振蕩模式.在S形不動點曲線的Fold分岔點附近，不動點吸引子可與諸如2n周期或混沌等不同類型的吸引子共存.研究表明，若慢變激勵振幅充分大，以致慢變量能越過Fold分岔點時，吸引子的共存會因Fold分岔而被破壞.于是，系統向原先共存的吸引子轉遷，由此產生了由Fold分岔所誘發的各類對稱式簇發.另一方面，當慢變激勵無法越過Fold分岔點時，延遲分岔現象形成了不穩定的2n軌道與穩定的2n+1(n=0,1,2,··)軌道間的滯后.基于此，得到了由延遲Flip分岔所誘發的各種非對稱式簇發.特別的，本文所報道的簇發其“激發態”大多由兩次以上的反向Flip分岔才過渡到“沉寂態”，從而導致簇發具備多級反向Flip分岔這類復雜的結構.然而，需要指出的是，本文的研究主要針對簇發動力學機制的定性分析，仍有一些與簇發相關的重要問題需進一步探討，例如簇發中延遲現象的本質以及延遲量的計算等問題.

1 Izhikevich EM.Neural excitability,spiking and bursting.Int J Bifurcat Chaos,2000,10(6)：1171-1266

2 Izhikevich EM.Resonance and selective communication via bursts in neurons having subthreshold oscillations.Bio Systems,2002, 67(1-3)：95-102

3 古華光，朱洲，賈冰.一類新的混沌神經放電的動力學特征的實驗和數學模型研究.物理學報,2011,60(10)：1005051-10050512 (Gu Huaguang,Zhu Zhou,Jia Bing.Dynamics of a novel chaotic neural firin pattern discovered in experiment and simulated in mathematical model.Acta Phys Sin,2011,60(10)：1005051-10050512(in Chinese))

4 王帥,于文浩,陳巨輝等.鼓泡流化床中流動特性的多尺度數值模擬.力學學報，2016,48(3)：585-592(Wang Shuai,Yu Wenhao, Chen Juhui,et al.Multi-scale simulation on hydrodynamic characteristics in bubbling fluidize bed.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3)：585-592(in Chinese))

5 Li XH,Bi QS.Single-Hopf Bursting in periodic perturbed Belousov—Zhabotinsky reaction with two time scales.Chinese Phys Lett,2013,30(1)：10503-10506

6 Li XH,Zhang C,Yu Y,et al.Periodic switching oscillation and mechanism in a periodically switched BZ reaction.Sci China E, 2012,55(10)：2820-2828

7 Lashina EA,Chumakova NA,Chumakov GA,et al.Chaotic dynamics in the three-variable kinetic model of CO oxidation on platinum group metals.Chem Eng J,2009,154(1-3)：82-87

8 賈宏濤,許春曉,崔桂香.槽道湍流近壁區多尺度輸運特性研究.力學學報,2007,39(2)：181-187(Jia Hongtao,Xu Chunxiao,Cui Guixiang.Multi-scale energy transfer in near-wall region of turbulent channel fl w.Chinese Journal of Theoretical and Applied Mechanics,2007,39(2)：181-187(in Chinese))

9 Clarke RJ,Apell HJ,Kong BY.Allosteric ef f ect of ATP on,Na+, K+-ATPase conformational kinetics.Biochemistry,2007,46(23)：7034-7044

10 郭建俠,卞林根,戴永久.玉米生育期地表能量平衡的多時間尺度特征分析及不平衡原因的探索.中國科學D,2008,38(9)：1103-1111(Guo Jianxia,Bian Lingen,Dai Yongjiu.Analysis of characteristics of multiple time scale in surface energy balance of corn in growth period,and exploration of the reasons for unbalance.Sci China D,2008,38(9)：1103-1111(in Chinese))

11 Courbage M,Nekorkin VI,Vdovin LV.Chaotic oscillations in a map-based model of neural activity.Chaos,2007,17(4)：155-160

12 Butera Jr RJ,Rinzel J,Smith JC.Models of respiratory rhythm generation in the pre-Btzinger complex.II.populations of coupled pacemaker neurons.J Neurophysiol,1999,82(1)：398-415

13 RinzelJ.Bursting oscillation in an excitablemembrane model//Everitt WN,Sleeman BD.Lecture Note In Mathematics. Vol.1151.New York：Springer,1985：304-316

14 楊卓琴，陸啟韶.神經元Chay模型中不同類型的簇放電模式.中國科學G,2007,37(4)：440-450(Yang Zhuoqin Lu Qishao.Dif f erent types of bursting spiking mode in Chay model of neurons.SciChina G,2007,37(4)：440-450(in Chinese))

15 Rulkov NF.Regularization of synchronized chaotic bursts.Phys Rev Lett,2001,86(1)：183-186

16 Wagenaar DA,Pine J,Potter SM.An extremely rich repertoire of bursting patterns during the development of cortical cultures.BMC Neurosci,2006,7(1)：1-18

17 古華光，惠磊，賈冰.一類位于加周期分岔中的貌似混沌的隨機神經放電規律的識別.物理學報,2012,61(8)：0805041-08050410 (Gu Huaguang,Hui Lei,Jia Bing.Identificatio of a stochastic neural firin rhythm lying in period-adding bifurcation and resembling chaos.ActaPhysSin,2012,61(8)：0805041-08050410(inChinese))

18 Channell P,Cymbalynk G,Shilnikov A.Applications of the Poincar′e mapping technique to analysis of neuronal dynamics.Neurocomputing,2007,70(10-12)：2107-2111

19 Izhikevich EM,Hoppensteadt F.Classficatio of bursting mapping.Int J Bifurcat Chaos,2004,14(11)：3847-3854

20 Courbage M,Maslennikov OV,Nekorkin VI.Synchronization in time-discrete model of two electrically coupled spike-bursting neurons.Chaos Soliton Fract,2012,45(5)：645-659

21 Maslennikov OV,Nekorkin VI.Discrete model of the olivocerebellar system：structure and dynamics.Radiophys Quant El, 2012,55(55)：198-214

22 Nekorkin VI,Maslennikov OV.Spike-burst synchronization in an ensemble of electrically coupled discrete model neurons.Radiophys Quant El,2011,54(1)：56-73

23 Stoyanov B,Kordov K.Novel image encryption scheme based on Chebyshev polynomial and Duffing map.Scientifi World J,2014, 2014：283639-283639

24 Kuehn C.Multiple Time Scale Dynamics.New York：Springer, 2015：8-14

25 Han XJ,Bi QS.Bursting oscillations in Duffing’s equation with slowly changing external forcing.Commun Nonlinear Sci Numer Simul,2011,16(10)：4146-4152

26 張曉芳，陳小可，畢勤勝.快慢耦合振子的張馳簇發及其非光滑分岔機制.力學學報，2012,44(3)：576-583(Zhang Xiaofang,Chen Xiaoke,Bi Qinsheng.Relaxation bursting of a fast-slow coupled oscillation as well as the mechanism of non-smooth bifurcation.Chinese Journal of Theoretical and Applied Mechanics,2012,44(3)：576-583(in Chinese))

27 Han XJ,Bi QS.Slow passage through canard explosion and mixed mode oscillations in the forced Van der Pol’s equation.Nonlinear Dyn,2012,68(1-2)：275-283

28 Bear SM,Erneux T,Rinzel J.The slow passage through a Hopf bifurcation：delay,memory ef f ects,and resonance.SIAM J Appl Math, 1989,49(1)：55-71

29 BaesensC.Slowsweepthroughaperiod-doublingcascade：Delayed bifurcations and renormalisation.Physica D,1991,53(2-4)：319-375

30 Han XJ,Bi QS,Zhang C,et al.Study of mixed-mode oscillations in a parametrically excited van der Pol system.Nonlinear Dyn,2014, 77(4)：1285-1296

31 Tzou JC,Ward MJ,Kolokolnikov T.Slowly varying control parameters,delayed bifurcations,and the stability of spikes in reactiondif f usion systems.Physica D,2015,290：24-43

COMPLEX BURSTING OSCILLATION STRUCTURES IN A TWO-DIMENSIONAL NON-AUTONOMOUS DISCRETE SYSTEM1)

Chen Zhenyang Han Xiujing2)Bi Qinsheng
(Faculty of Civil Engineering and Mechanics，Jiangsu University，Zhenjiang212013，Jiangsu，China)

Bursting oscillations are the archetypes of complex dynamical behaviors in systems with multiple time scales, and the problem related to dynamical mechanisms and classification of bursting oscillations is one of the important problems in bursting research.However,up to now,most of the structures of bursting revealed by researchers are relatively simple.In this paper,we take the non-autonomous discrete Duffing system as an example to explore novel bursting patterns with complex bifurcation structures,which are divided into two groups,i.e.,symmetric bursting induced by Fold bifurcations and asymmetric bursting induced by delayed Flip bifurcations.Typically,the fast subsystem exhibits an S-shaped fi ed point curve with two Fold points,and the stable upper and lower branches evolve into chaos by a cascade of Flip bifurcations.When the non-autonomous term(i.e.,the slow variable)passes through Fold points,transitions to various attractors(e.g.,periodic orbits and chaos)on the stable branches may take place,which accounts for the appearance of Fold-bifurcation-induced symmetric bursting patterns.If the non-autonomous term is not able to pass through Fold points,but to go through Flip points,delayed Flip bifurcations can be observed.Based on this,delayed-Flip-bifurcation-induced asymmetric bursting patterns are obtained.In particular,the bursting patterns reported here exhibit complex structures containing inverse Flip bifurcations,which has been found to be related to the fact that the nonautonomous term slowly passes through Flip points of the fast subsystem in an inverse way.Our results enrich dynamical mechanisms and classification of bursting in discrete systems.

discrete Duffing system,complex bursting patterns,delayed Flip bifurcations,inverse Flip bifurcation structures

O322

A doi：10.6052/0459-1879-16-267

2016-09-22收稿，2016-11-06錄用,2016-11-11網絡版發表.

1)國家自然科學基金(11572141,11632008,11502091,11472115,11402226)和江蘇大學青年骨干教師培養工程資助項目.

2)E-mail：xjhan@mail.ujs.edu.cn

陳振陽，韓修靜，畢勤勝.一類二維非自治離散系統中的復雜簇發振蕩結構.力學學報,2017,49(1)：165-174

Chen Zhenyang,Han Xiujing,Bi Qinsheng.Complex bursting oscillation structures in a two-dimensional non-autonomous discrete system.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1)：165-174