磁感應強度和阻尼通道間隙對某發射裝置振動影響

趙致富,葛建立,張鴻浩,楊國來

(1.南京理工大學 機械工程學院,南京 210094; 2.北京特種機電研究所,北京 100012)

【裝備理論與裝備技術】

磁感應強度和阻尼通道間隙對某發射裝置振動影響

趙致富1,葛建立1,張鴻浩2,楊國來1

(1.南京理工大學 機械工程學院,南京 210094; 2.北京特種機電研究所,北京 100012)

本文主要研究磁流變阻尼器應用在高速、高沖擊性環境下發射裝置的反后坐裝置中，其結構參數磁感應強度和阻尼通道間隙對發射裝置的振動影響；采用有限元和abaqus軟件二次開發平臺相結合的方法建立該發射裝置結構動力學有限元模型，改變磁流變阻尼器的結構參數模擬整個裝置的發射過程，研究發射裝置的振動特性。仿真計算結果表明，輸入不同的電流值和不同的阻尼通道間隙值會對發射裝置振動特性產生影響，在設計和應用發射裝置上磁流變阻尼器時應給予重視。

磁流變阻尼器；高速沖擊；反后坐裝置；振動特性

以磁流變液為介質設計的磁流變阻尼器(MR)是一種新型的半主動控制裝置，目前對磁流變阻尼器的研究主要集中在低頻、低速或隨機載荷下的振動控制領域。磁流變阻尼器在高速、高沖擊載荷下的研究相對滯后，尤其是將其應用在武器系統反后坐裝置中，其優越的性能取決于阻尼器的結構參數，其中最主要的參數是輸入電流值和阻尼通道間隙的大小，因此，研究輸入電流和阻尼通道間隙對發射裝置振動特性的影響對于磁流變阻尼器的設計有重大意義。

由于磁流變阻尼器的優越性能，磁流變阻尼器在各領域中得到了廣泛的應用，針對磁流變阻尼器在高速沖擊環境下的性能進行了深入研究。Lee Dug Young推導了磁流變液模型描述公式[1]。J.M.Ko等闡述了阻尼器建模方法及其應用[2]。張莉潔通過實驗平臺測試了磁流變阻尼器在高速沖擊環境下的動態特性并做了分析[3]。侯保林研究了應用在艦炮上的磁流變阻尼器的本構模型以及模型參數的影響[4]。Ahmadian 等將磁流變阻尼器應用在中到大口徑的槍械系統，研究結果顯示磁流變阻尼器可減小后坐力、提高射擊精度和系統穩定性[5]。李良軍通過設計磁流變阻尼器參數并對某型號火炮后坐過程進行計算仿真動態分析，驗證了沖擊載荷下磁流變阻尼器應用的可行性[6]。胡紅生通過沖擊載荷激勵作用的阻尼器動態響應實驗平臺驗證了磁流變阻尼器優越的性能和可控性[7]。張俊飛、李強建立了某大口徑火炮的有限元模型，分析了火炮結構參數對火炮振動特性的影響[8]、[9]。賈長治通過研究緩沖裝置動態特性改進仿真方法，提高仿真結果的可靠性[10]。目前關于磁流變阻尼器的研究和在生活中的應用較為廣泛，但是在高速、高沖擊武器發射領域研究相對滯后，磁流變阻尼器結構參數對高速發射裝置的振動特性影響的研究處于起步階段。

針對現有文獻中磁流變阻尼器的設計幾乎都是以阻尼力和阻尼力可調范圍兩個設計指標計算阻尼器結構參數，本文建立了整個發射裝置的有限元動力學模型，并計算仿真，得出磁流變阻尼器的關鍵結構參數磁感應強度和阻尼通道間隙對發射裝置振動特性的影響規律，為專用磁流變阻尼器的結構設計提供新的思路。

1 發射裝置結構有限元建模

1.1 發射裝置組成及工作

以圖1示意的某發射裝置為研究對象，該發射裝置主要由后坐部分、外筒、阻尼器安裝座、磁流變阻尼器和滑軌等部件組成。發射裝置發射時，炮膛合力提供后坐動力，迫使后坐部分(包括身管、支架等后坐部件)向后運動，而后坐阻力由兩個對稱布置的磁流變阻尼器提供，同時為裝置復進提供動力。在炮膛合力的作用下，后坐部分沿滑軌向圖中箭頭方向后坐，后坐位移從零到最大位移處，速度從零加速到最大值再減速到零值，后坐過程結束。在磁流變阻尼器中復進簧的作用下完成后坐部分的復進到位過程。

圖1 發射裝置示意圖

1.2 發射裝置有限元建模

根據有限元建模方法利用Hypermesh軟件對發射裝置結構進行網格劃分。對阻尼器安裝座、滑軌、身管均采用縮減積分六面體單元進行劃分；對外筒、支架等鈑金件采用縮減積分殼單元進行劃分，單元類型以矩形為主，含少量三角形；對緩沖器采用連接器、彈簧單元和質量單元進行模擬。為了便于輸出炮口處的特征參數變量，將炮口中心點設置為參考點，并用耦合約束連接該參考點與炮口處的單元節點。為提高建模和計算效率，對小圓孔、圓角和倒角等進行簡化處理。為了保證計算精度與準確性，對主要零部件結構應保證網格與實體的一致性，而且在關鍵位置進行網格細化。整個發射裝置中，對于復雜的連接關系也必須進行妥善處理。通過在身管和支架上建立剛體約束模擬兩者之間的連接關系；通過建立綁定約束，模擬阻尼器安裝座與外筒、支座與安裝板、滑軌支座與外筒等連接關系；通過建立耦合約束，模擬滑軌上法蘭盤與滑桿、滑桿與支座以及阻尼器安裝座上支座和銷、銷和拉桿等區域的接觸碰撞關系。通過建立連接器，利用abaqus軟件二次開發平臺開發程序模擬磁流變緩沖器在受力情況下的運動關系。

1.3 施加載荷與邊界條件

該發射裝置在發射過程中，彈丸在身管膛內運動時間非常短，運動和受力情況較為復雜。發射過程中受的主動力為炮膛合力；而受到的其他外力主要是磁流變阻尼器提供的阻尼力和彈簧力，包括因磁場產生的庫侖阻尼力、液體自身產生的黏滯阻尼力、密封處的摩擦力和復進彈簧產生的彈力；后坐復進運動過程中，滑軌上法蘭盤和滑桿之間的摩擦接觸會產生相應的摩擦力。在本研究中，炮膛合力對發射裝置的作用是通過在身管上施加一個隨時間變化的脈沖載荷等效壓力模擬；而阻尼力則是通過在阻尼器與緩沖座和支架后板上的支座的連接點上施加一對共線且反向的隨時間變化的集中力模擬，力的大小采用abaqus二次開發的Fortran程序施加；復進彈簧力則通過建立彈簧單元模擬彈簧隨位移變化產生的彈力；滑軌上產生的摩擦力通過設置接觸碰撞關系和設置摩擦因數模擬。在發射裝置外筒后端面上施加全約束邊界條件。脈沖載荷隨時間變化曲線如圖2所示，發射裝置受力分析如圖3所示。

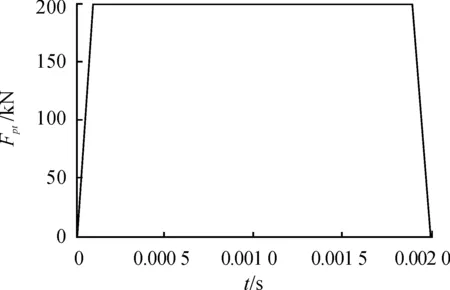
圖2 脈沖載荷等效壓力隨時間變化曲線

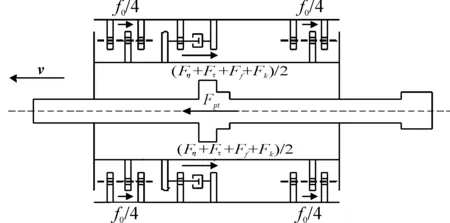
圖3 發射裝置受力分析示意圖

2 磁流變阻尼器建模與阻尼力的計算方法

根據1.3小節的圖3受力分析可以建立如下運動微分方程方程：

FR=Fη+Fτ+Ff+Fk

式中，m是后坐質量(kg)；Fpt是炮膛合力(N)；FR是磁流變阻尼器產生的總阻尼力(N)，包括與速度有關的黏滯阻尼力Fη、隨磁場改變的庫倫阻尼力Fτ、隨液體壓力改變的O型密封圈處的摩擦力Ff和復進彈簧產生的彈簧力Fk；f0是滑軌上法蘭盤與滑桿的滑動接觸摩擦力(N)。

圖4是研究的磁流變阻尼器的結構示意圖。該旁通閥式磁流變阻尼器由彈簧與磁流變阻尼裝置集成，它具有磁流變缸和主缸兩個油缸，勵磁線圈纏繞在磁流變缸活塞上，二者形成一個磁通回路，使活塞與油缸形成的環狀流口的磁流體具有一定的磁通密度，達到一定的屈服應力。

圖4 磁流變阻尼器結構示意圖

2.1 磁流變液本構特性模型

由于磁流變阻尼器自身的Bingham黏塑性特性，磁流變阻尼器的動力測試曲線表現出明顯的非線性滯回特性。為簡化模型，考慮磁流體會出現剪切稀化現象，選擇Bingham模型進行阻尼器建模，描述磁流體的本構特性模型可用下式表示[3]：

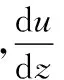
2.2 阻尼力的計算

依據經典的流變力學理論，可推導得到剪切閥式磁流變阻尼器的阻尼力簡化計算模型，即Bingham平板模型，該模型的阻尼力為[6]：

式中，Fη是與速度有關的黏滯阻尼力(N)；Fτ是隨磁場而改變的庫倫阻尼力(N)；η是磁流體的零場黏度(kPa·s)；L是活塞有效激活長度(mm)，即有效磁極寬度；Ap是活塞有效面積(mm2)；h是活塞與缸體間的阻尼通道間隙(mm)；D′是阻尼通道平均周長(mm)；τy是磁流體的剪切屈服強度(kPa)；v是活塞相對于缸體的運動速度(mm/s)。

考慮到阻尼器工作過程中的密封性，采用的O形密封圈處的摩擦力也要加以考慮，O形密封圈處的摩擦力Ff為[11]：

式中，fc是由O型圈的摩擦因數，fy是由磁流體壓力引起附加摩擦因數，D是圓環狀矩形槽直徑(mm)，d是相對運動的表面直徑 (mm)，p是磁流體壓力(MPa)。

彈簧是為后坐部分復進提供動力的部件，彈簧的參數為：預壓力240 N，剛度為10 N/mm。彈簧產生的力為：

Fk=240+10x

為求得阻尼器的阻尼力，首先需要確定流口中激活區的磁流體的屈服應力τy，根據實驗測得的MRF的τ-B曲線，利用Matlab軟件對曲線擬合，生成表示屈服應力τy的近似的數學函數式可表示為：

τy=43.44B4-178.12B3+183.74B2-3.02B

式中，τy為屈服應力(kPa)，磁感應強度T(Tesla)。

3 磁流變阻尼器參數對發射裝置后坐特性的影響

3.1 磁流變阻尼器影響參數的選取

MR阻尼器所產生的阻尼力由黏滯阻尼力(與液體黏度有關)、庫倫阻尼力(隨磁場改變)、彈簧力(隨位移改變)和摩擦力(隨液體壓力改變)組成。黏滯阻尼力由阻尼器結構參數和活塞運動速度決定；庫倫阻尼力由結構參數和MR流體屈服應力決定，而MR流體屈服應力取決于通過阻尼器的磁感應強度。在本研究中，選擇磁感應強度B和阻尼通道間隙h作為參考變量。結構參數值得選取如表1所示。

表1 影響結構參數選取值

3.2 發射裝置仿真結果與分析

為了仿真真實的反應后坐過程，采用abaqus有限元軟件，并嵌入Fortran程序實現二次開發，設置傳感器準確實時的模擬后坐過程各參數值，對全炮模型進行有限元仿真分析。這里選擇兩個主要的參數值：磁感應強度B和阻尼通道間隙h。以炮口各振動特性參數為研究對象，得到不同參數值對發射裝置后坐特性的影響。

圖5～圖8分別是發射裝置在相同沖擊載荷、不同的外加電流作用下(即不同的磁感應強度B作用下)的位移和速度曲線。由于不同外加電流作用下后坐時間不同，對炮口豎直方向振動位移速度圖時間采取歸一化處理。

圖5 身管后坐位移-時間曲線

圖7 炮口豎直方向位移-時間曲線

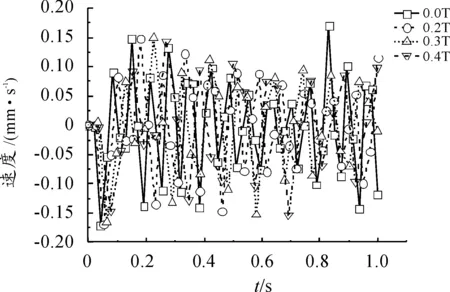
圖8 炮口豎直方向速度-時間曲線

由圖5～圖8可以看出：

(1)在磁感應強度為0.0T、0.2T、0.3T、0.4T時，后坐位移分別為21.75 mm、17.40 mm、13.99 mm、11.74 mm，后坐速度分別為645.17 mm/s、630.41 mm/s、615.64 mm/s、600.95 mm/s，后坐時間分別為0.070 5 s、0.058 5 s、0.046 5 s、0.039 s，炮口豎直方向位移最大值分別為2.54E-4 mm、1.08E-4 mm、1.51E-4 mm、1.42E-4 mm，速度最大值分別為0.17 mm/s、0.16 mm/s、0.16 mm/s、0.15 mm/s。

(2)由后坐的位移-時間曲線和速度-時間曲線可知，隨著電流的增加，位移-時間曲線在相同時間內后坐位移的增長幅度逐漸減小，且最大位移值相差明顯；速度-時間曲線后坐速度峰值呈現減小趨勢且相差不大，而速度下降階段是隨著電流的增大速度下降越快。

(3)由炮口振動的位移-時間曲線和速度-時間曲線可知，隨著電流的增加，炮口振動位移和速度均相應增加，且在后期振動幅度更大。因此在后坐的整個動態過程范圍內，可以實時控制輸入電流，控制后坐位移長度和炮口振動。

圖9～圖12分別是發射裝置在相同沖擊載荷、相同外加電流作用下(即相同磁感應強度作用下)、不同阻尼通道間隙值的位移-時間曲線和和速度-時間曲線。由于不同阻尼通道間隙下后坐時間不同，對炮口豎直方向振動位移速度圖時間采取歸一化處理。

圖9 身管后坐位移-時間曲線

圖10 身管后坐速度-時間曲線

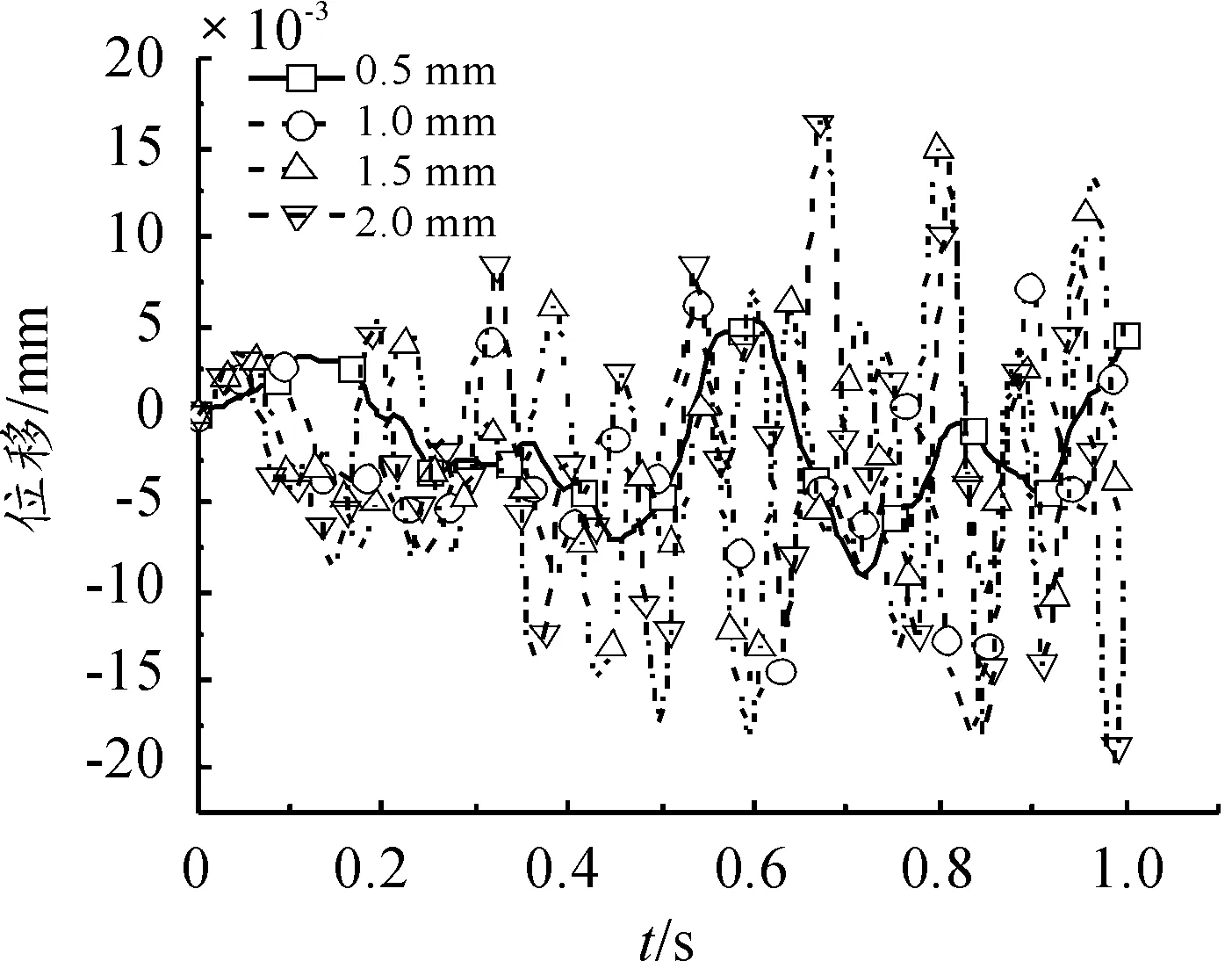
圖11 炮口豎直方向位移-時間曲線

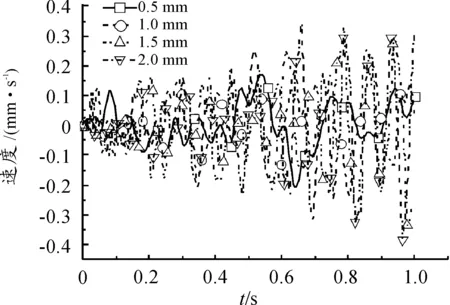
圖12 炮口豎直方向速度-時間曲線

由圖9～圖12可以看出：

(1)在阻尼通道間隙為0.5 mm、1.0 mm、1.5 mm、2.0 mm時，后坐位移分別為3.48 mm、6.94 mm、9.82 mm、12.20 mm，后坐速度分別為555.94 mm/s、599.03 mm/s、614.59 mm/s、624.18 mm/s，后坐時間分別為0.012 s、0.023 s、0.032 s、0.038 s，炮口豎直方向位移最大值分別為9.01E-5 mm、1.80E-4 mm、1.82E-4 mm、1.87E-4 mm，速度最大值分別為0.21 mm/s、0.24 mm/s、0.34 mm/s、0.38 mm/s。

(2)由后坐的位移-時間曲線和速度-時間曲線可知，隨著阻尼通道間隙的增加，位移-時間曲線在相同時間內后坐位移的增長幅度逐漸增加，且最大位移值變化很大，速度-時間曲線峰值呈現逐漸增大的趨勢且相差不大，而速度下降階段隨著阻尼通道間隙的增加減緩。

(3)由炮口振動的位移-時間曲線和速度-時間曲線可知，隨著阻尼通道間隙值的增加，炮口振動位移和速度前期變化規律大致相同，呈增長趨勢，而在后期振動幅度變化更大。因此在后坐的整個動態過程范圍內，在保證結構剛度滿足要求的前提下，盡量減小阻尼通道間隙。

4 結論

磁感應強度對發射裝置后坐位移和炮口振動有顯著影響，可以通過實時控制輸入電流控制后坐位移長度和炮口振動，實現理想的運動規律；磁流變阻尼器的阻尼通道間隙對發射裝置后坐位移和炮口振動也有較大的影響，在保證滿足結構剛度要求的前提下，選取較小的阻尼通道間隙有利于減小后坐位移、后坐時間、減小炮口振動和提高射擊精度。

本文僅考慮了磁感應強度和阻尼通道間隙對后坐位移和炮口振動的影響，后續的研究工作將對其他結構參數的影響進行分析，并對整個裝置優化，以獲得最佳性能要求。本文的研究對發射裝置緩沖器的合理設計具有一定的參考價值。

[1] LEE DUG YOUNG.WERELEY N M.Quasi steady Herschel-Bulkley analysis of electro and magneto rheological flow mode dampers[J].Journal of Intelligent Material Systems & Struetures,2000,10(10):761-769.

[2] KO J M,NI Y Q.Modeling of a full-scale MR damper and its application in open-loop vibration control of stay cables[J].Smart Structure and Materials 2005:Damping and isolation.SPIE Vol.5765 (2005):690-700.

[3] 張莉潔.沖擊載荷下磁流變阻尼器動態特性分析及其控制系統設計[D].南京:南京理工大學,2008.

[4] 侯保林.基于Herschel-Bulkley模型的火炮磁流變后坐阻尼器設計與分析[J].振動與沖擊,2006,25(3):6-10.

[5] AHMADIAN M,NORRIS J A.Experimental analysis of magnetorheological dampers when subjected to impact and shock loading[J].Communication in Nonlinear Science and Numerical Simnlation,2008,13:1978-1985.

[6] 李良軍.磁流變沖擊阻尼器在火炮反后坐裝置中的應用研究[D].南京:南京理工大學,2006.

[7] 胡紅生,王炅，蔣學爭，等.火炮磁流變后坐阻尼器的設計與可控性分析[J].振動與沖擊,2010,29(2):184-188.

[8] 張俊飛.某火炮結構參數靈敏度分析與優化研究[D].南京:南京理工大學,2014.

[9] 李強.影響彈丸起始擾動的某火炮結構參數分析與優化研究[D].南京:南京理工大學,2015.

[10]賈長治.火炮沖擊緩沖裝置動態特性影響仿真分析與改進方法[J].機械工程學報,2012，48(19):156-162.

[11]高躍飛.火炮反后坐裝置設計[M].北京:國防工業出版社,2010.

(責任編輯 周江川)

Impact of Magnetic Induction and Damping Channel Clearance on the Vibration of a Launching Device

ZHAO Zhi-fu1, GE Jian-li1, ZHANG Hong-hao2, YANG Guo-lai1

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2.Beijing Institute of Special Electromechanical Technology, Beijing 100012, China)

This paper mainly studied the influence of magnetic induction and damping channel clearance, which is used in the recoil device of a launcher working in a high speed and high impact environment. Finite element method and the secondary program development platform in ABAQUS were combined to establish the structural dynamic finite element model of the launcher. The launch process of the whole device was simulated by changing the structural parameters of MR dampers, and the vibration characteristics of the launcher were obtained. The simulation results show that the different value of the input current and the gap of different damping channel could influence the characteristics of the launcher, and attention should be paid to the design and application of MR damper on the launcher.

magnetorheological damper; high-speed impact; recoil system; vibration characteristics

2016-10-07；

2016-11-05

中央高校基本科研業務費專項資金項目(30915118825);國家重大科學儀器設備開發專項(2013YQ470765)

趙致富(1990—)，男，碩士研究生，主要從事非線性有限元仿真研究。

葛建立(1980—),男，博士，副教授，主要從事非線性有限元、虛擬樣機以及等幾何分析研究。

10.11809/scbgxb2017.02.011

趙致富,葛建立,張鴻浩,等.磁感應強度和阻尼通道間隙對某發射裝置振動影響[J].兵器裝備工程學報，2017(2):43-47.

format:ZHAO Zhi-fu, GE Jian-li, ZHANG Hong-hao, et al.Impact of Magnetic Induction and Damping Channel Clearance on the Vibration of a Launching Device[J].Journal of Ordnance Equipment Engineering,2017(2):43-47.

TJ866

A

2096-2304(2017)02-0043-05