平均法在不確定系統穩定性分析中的應用

王培光，候娟娟

(河北大學 數學與信息科學學院,河北 保定 071002)

?

平均法在不確定系統穩定性分析中的應用

王培光，候娟娟

(河北大學 數學與信息科學學院,河北 保定 071002)

討論了一類含參數的不確定系統,運用平均法,得到了該系統漸近穩定的結果,并給出了實例驗證.

平均法；不確定系統；漸近穩定性

MSC 2000：34D20；34A37

在許多實際工程應用中,幾乎所有可運行的系統均要求設計是穩定的,但由于系統自身的復雜性,尋求解析解是十分困難的,因而從理論上探討解的穩定性是一項有意義的工作.如果一個系統不僅僅依賴于某一時刻的狀態,而且還依賴于某種不確定因素,則稱該系統為不確定系統[1].Sundarapandian等[2]提出了參數穩定性的概念,并且應用Lyapunov 直接方法分析了不確定參數穩定性問題之后,Ohta等[3]提出了非線性不確定系統平衡位置的穩定性問題,Martynyuk等[4]通過運用不同的Lyapunov函數分析了不確定系統的運動穩定性.這些理論大都運用Lyapunov函數方法討論不確定系統穩定性問題.

平均法可避免構造Lyapunov 函數帶來的困難,Gama等[5]用平均法討論了右端不連續系統的穩定性問題.本文將平均法應用于不確定系統,得到了不確定參數系統穩定性的充分條件,發展和豐富了不確定系統穩定性理論.

1 預備知識

本文討論不確定系統

(1)

及其不確定平均系統

(2)

為得到本文主要結果,首先給出如下定義及引理.

定義1[4]稱系統(1)在參數α處是參數穩定的,若系統(1)滿足下列條件：

A1)存在平衡態xe(α)∈Rn,其中xe:Rd→Rn為向量參數函數,xe=xe(α),α∈Rd;

A2) 對任意的ε>0,存在δ=δ(ε,α)>0,當‖x0-xe(α)‖<δ時,有

‖x(t,α)-xe(α)‖<ε

對任意的t∈R+成立.

定義2[4]稱系統(1)在參數α處是參數漸近穩定的,若系統(1)滿足下列條件：

A3) 系統(1)在參數α處是參數穩定的；

A4)存在參數β的開領域N(β),對任意的α∈N(β),存在μ(α)>0,當‖x0-xe(α)‖<μ時,有

成立.

引理1 給定η>0,存在ε0>0,使得對任意的ε∈[0,ε0],有{x(t)}?{y(t)}+ηB成立.其中B={x∈Rn|‖x‖≤1},{x(t)},{y(t)}分別為系統(1)系統(2)解的集合.

證明：反證法.假設不然,即x(t)∈{x(t)},但x(t){y(t)}+ηB.

令τ2>τ1,那么

(3)

對(3)式兩邊同時除以τ2-τ1,且兩邊同時取極限得

(4)

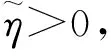
所以存在η>0,系統(1)的解x(t)與系統(2)的解y(t)滿足{x(t)}?{y(t)}+ηB.

2 主要結果

將運用平均法證明不確定系統與其平均系統解之間的逼近關系,并且進一步證明不確定系統的漸近穩定性.

定理1 假設

(H1)函數f∈C([t0,∞)×Rn×Rd),且滿足‖f‖≤M,‖f(s,x(s),α)-f(s,y(s)，β)‖≤λ(‖x(s)-y(s)‖+‖α-β‖),其中λ>0,M為常數,α,β∈S?Rd是向量物理參數,d≥1,S是緊集；

(H2)參數α,β滿足‖α-β‖≤q,其中q>0為常數.

則對任意的η>0和給定的L>0,存在ε∈(0,ε](ε0=ε0(η,L)),使得對0<ε<ε0,系統(1)的解x(t)與系統(2)的解y(t)滿足

‖x(t)-y(t)‖≤η,0≤t≤Lε-1.

證明：首先注意到,(1)的解滿足以下積分方程

(5)

且(2)的解滿足

(6)

進一步得

(7)

由條件(H1)(H2),有

(8)

令L>0為固定數,對于0≤t≤Lλ-1,有

其中

‖f(s,y(s),β)-f0(y(s))‖ds.

并且

進一步得

T2≤2LM.

(9)

再根據(7)和(9)得

(10)

其中δ=2LM+ελqt.

由引理2,對(10)式應用Gronwall不等式得,

‖x(t)-y(t)‖≤δexp{λL},0≤t≤Lε-1.

更進一步得到

‖x(t)-y(t)‖≤η,t∈[0,Lε-1].

定理1的證明到此完成.

定理2的證明到此完成.

推論1 假設

(H1)函數f∈([t0,∞)×Rn×Rd),且f(t,x,α)是周期為T的周期函數,且滿足‖f‖≤M,‖f(s,x(s),α)-f(s,y(s),β)‖≤λ(‖x(s)-y(s)‖+‖α-β‖),其中λ>0為常數α,β∈S?Rd, 是2個向量物理參數,d≥1,S是緊集;

(H2)參數α,β滿足‖α-β‖≤q,其中q>0為常數,則對任意的η>0和L>0,存在ε∈(0,ε](ε=ε0(η,L)),使得對0<ε<ε0,系統(1)的解x(t)與系統(2)的解y(t)滿足

‖x(t)-y(t)‖≤η,0≤t≤Lε-1.

推論1的證明同定理1證明過程類似,不再贅述.

推論2同定理2證明過程類似,不再贅述.

下面舉例說明定理的應用,運用平均法分析不確定系統穩定性問題.

3 例子

例1.考慮下列的不確定微分系統

及它的平均微分系統為

[1] 張子方,徐道義.不確定動力系統的穩定性及其應用[D].成都：四川大學, 2004. ZHANG Z F,XU D Y.The stability of uncertain dynamical systems and applications[D].Chengdu:Sichuan University,2004.

[2] SUNDARAPANDIAN V.New results on the parametric stability of nonlinear systems[J].Mathematical and Computer Modelling,2006,43:9-15.DOI:org/10.1016/j.mcm.2005.04.010.

[3] OHTA Y,SILJAK D D.Parametric quadratic stability of uncertain nonlinear systems[J].Systems and Control Letters,1994,22:437-444.DOI:10.1016/0167-6911(94)90087-6.

[4] MARTYNYUK A A,MARTYNYUK-CHERNIENKO Y A.Uncertain dynamical systems:stability and motion control[M].Boca Raton:Taylor and Francis Group,2012.

[5] GAMA R,GUERMAN A,SMIRNOV G.On the asymptotic stability of discontinuous systems analyzed via the averaging method[J].Nonlinear Anal:TMA,2011,74:1513-1522.DOI:10.1016/j.na.2010.10.024.

[6] 葛渭高,李翠哲,王宏洲.常微分方程與邊值問題[M].北京：科學出版社,2008.

(責任編輯：孟素蘭)

The stability of uncertain systems analyzed via the averaging method

WANG Peiguang,HOU Juanjuan

(College of Mathematics and Information Science,Hebei University,Baoding 071002，China)

The main purpose of this paper is to investigate the asymptotic stability of uncertain systems via the averaging method,and some corresponding results are obtained.We provide an example to illustrate our main results.

averaging method;uncertain systems;asymptotic stability

10.3969/j.issn.1000-1565.2017.01.001

2016-03-01

國家自然科學基金資助項目(11271106)；河北省自然科學基金資助項目(A2013201232)

王培光(1963—)，男，黑龍江哈爾濱人，河北大學教授，博士生導師，主要從事微分方程與控制理論的研究. E-mail:pgwang@hbu.edu.cn

O175.12

A

1000-1565(2017)01-0001-04