一種反演中高層大氣密度的新方法

周寶柱 陳金松 李清亮 李娜 唐楊,2

(1.中國電波傳播研究所 電波環境特性及模化技術重點實驗室,青島 266107; 2. 桂林電子科技大學信息與通信學院,桂林 541004)

引 言

中間層和低熱層(Mesosphere/Lower Thermosphere,MLT)區域中性大氣密度對于研究中高層大氣氣候、大氣動力學和大氣區域內O、O2和OH氣輝具有非常重要的意義,而連續測量MLT區域大氣密度的方法一直以來都是十分缺乏的．此外,中性大氣密度隨時間的變化是確定大氣阻力的關鍵信息,安全發射航天器,特別是低軌衛星和可控制的軌道衛星,同樣需要MLT區域中性大氣密度的準確知識．

工作在中頻(Medium Frequency, MF)到甚高頻(Very High Frequency, VHF)頻段的地基大氣雷達是研究MLT區域動態與結構的重要手段,但是它們通常沒法直接測量大氣密度．激光雷達能提供高時間分辨率和高精度的大氣密度剖面圖,但其需要在晴空條件下才能工作且很多雷達在夜間工作時都有一定限制．探空火箭也是一種探測中性大氣密度的有效手段,但是發射火箭的高成本和復雜的后勤使得常規檢測變得不切實際．

Hocking等人于2013年提出流星雷達技術并被廣泛用于研究MLT區域氣候和大氣動力學,包括風場和溫度[1]．2008年Stober等人提出流星雷達高度探測分布的峰值可以用來估計MLT區域的中性大氣密度變化[2]．Stober等人在2014年發現從2002年到2013年峰值高度的長期遞減是一個MLT區域中性大氣密度長期下降的現象,并發現主要原因是溫室氣體的冷卻[3]．流星雷達探測高度分布的峰值可以用來估計MLT區域的中性大氣密度變化,但是通過峰值高度的研究只能夠得到大氣密度的變化,不能確定大氣密度的準確值[4]．

2014年的第1到90天中國電波傳播研究所安裝在昆明觀測站的兩臺雷達開展了3個月的針對流星雷達觀測大氣的聯合觀測試驗．本文通過對該試驗數據的處理,提出一種利用流星雷達回波衰減時間確定的MLT區域雙極擴散系數[5]和利用大氣溫度梯度法[6-7]得到的溫度值共同反演中性大氣密度的方法．同時,通過不同高度的溫度梯度反演了不同高度的大氣密度,并將得到的大氣密度值與峰值高度對比,證明了流星雷達探測中高層大氣密度的可行性．

1 流星雷達

中國電波傳播研究所在昆明觀測站建立了一系列大氣雷達觀測系統(Kuming Atmospheric Radar Facility, KARF),該系統旨在研究低緯度地區低層與中層大氣的動力學和氣候學變化．其中包括一臺全天空流星雷達和一臺安裝全天空流星模式的ST雷達,這兩臺流星雷達由ATRAD 大氣雷達公司生產,同屬于Buckland Park全天空干涉流星雷達(Buckland Park All-sky Interferometic Meteor Radar, BPMR)系列,于2008年開始運行觀測[8]．

全天空流星雷達是目前世界上廣泛使用的中間層和低熱層區域大氣觀測手段．全天空流星雷達通過探測、接收和分析流星余跡回波的多普勒頻移,可以得到流星燒蝕區域(70～110 km)的背景大氣風場信息[5]．此外,還可以通過分析欠密度流星余跡回波的衰減時間來反演中間層頂區域(大約90 km和85 km)的中性大氣的溫度[6]．全天空流星雷達具有全天候連續觀測、無人值守、操作簡單、運行費用低廉、不受地域條件限制等特點,使其廣泛運用于世界各地．

昆明全天空流星雷達收發天線陣由1副相互正交兩單元八木天線作發射天線,5副交叉圓極化兩單元八木天線作接收天線組成[1]．表1給出了昆明全天空流星雷達和ST雷達的主要工作參數,可以看出兩臺雷達運行參數中只有發射機工作頻率和峰值輸出功率不同．

表1 流星雷達主要運行參數

2 流星雷達反演密度方法

微流星以11～72 km/s的速度進入地球大氣層,與大氣分子發生距離碰撞燒蝕形成等離子,一般的,在85～95 km高度內的流星余跡等離子體會以雙極擴散的形式擴散．在此條件下,流星雷達接收的欠密流星余跡反射回波其振幅會隨時間呈指數衰減,通過估算欠密流星余跡回波的衰減時間可以得到流星余跡雙極擴散的擴散系數[1],公式如下:

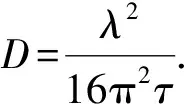
(1)

式中：λ為流星雷達的波長;τ為回波振幅由最大值衰減到其一半的時間;D為流星余跡等離子體擴散速率,即雙極擴散系數．

比較Yiwen提出的昆明流星雷達雙極擴散系數與衛星數據D值和高度的函數[6],可以發現在85 km到94 km之間,D的值是完全一致的,所以同樣的物理規律在此高度上是相同的．可得到雙極擴散系數D受背景大氣溫度、壓強和密度影響,且存在如下關系[9-11]:

(2)

式中：T、P和ρ分別表示中性大氣溫度、壓強和密度；K0是常數.因此,在知道大氣溫度的情況下,利用流星雷達觀測的雙極擴散系數D可以得到大氣壓強或者大氣密度[4,6-7,9].反之,知道大氣壓強或者大氣密度也可以得到大氣溫度[12-13]．

為了提高反演溫度的精確度需要剔除部分流星回波,去除回波種類如下:

1)剔除回波天頂角(zenith)大于55°的數據．回波天頂角越大,通過距離與天頂角計算得到的流星回波高度誤差越大．另外,流星進入地球大氣存在入射角,使得雷達探測到的流星天頂角大部分大于45°．因此,在保障回波高度精確度和流星回波數量情況下,昆明流星雷達選取天頂角小于55°的數據．

2)剔除高度太低但擴散系數很大(衰減時間很短)或高度太高但擴散系數很小(衰減時間很長)的流星回波．根據擴散系數與高度的關系曲線,各剔除水平和垂直方向上5%的數據．

通過溫度梯度法反演中間層頂的大氣溫度[6], 計算公式如下:

(3)

式中：T表示流星峰值高度處的中性大氣溫度；S表示lgD在高度分布上的斜率;dT/dz表示垂直溫度梯度;m表示空氣分子質量;k為波爾茲曼常數．本文直接利用溫度梯度法(式(3))反演的溫度,結合昆明流星雷達觀測的雙極擴散系數D,通過公式(2)反演85～94 km的中性大氣密度ρ．

3 數據驗證以及結果分析

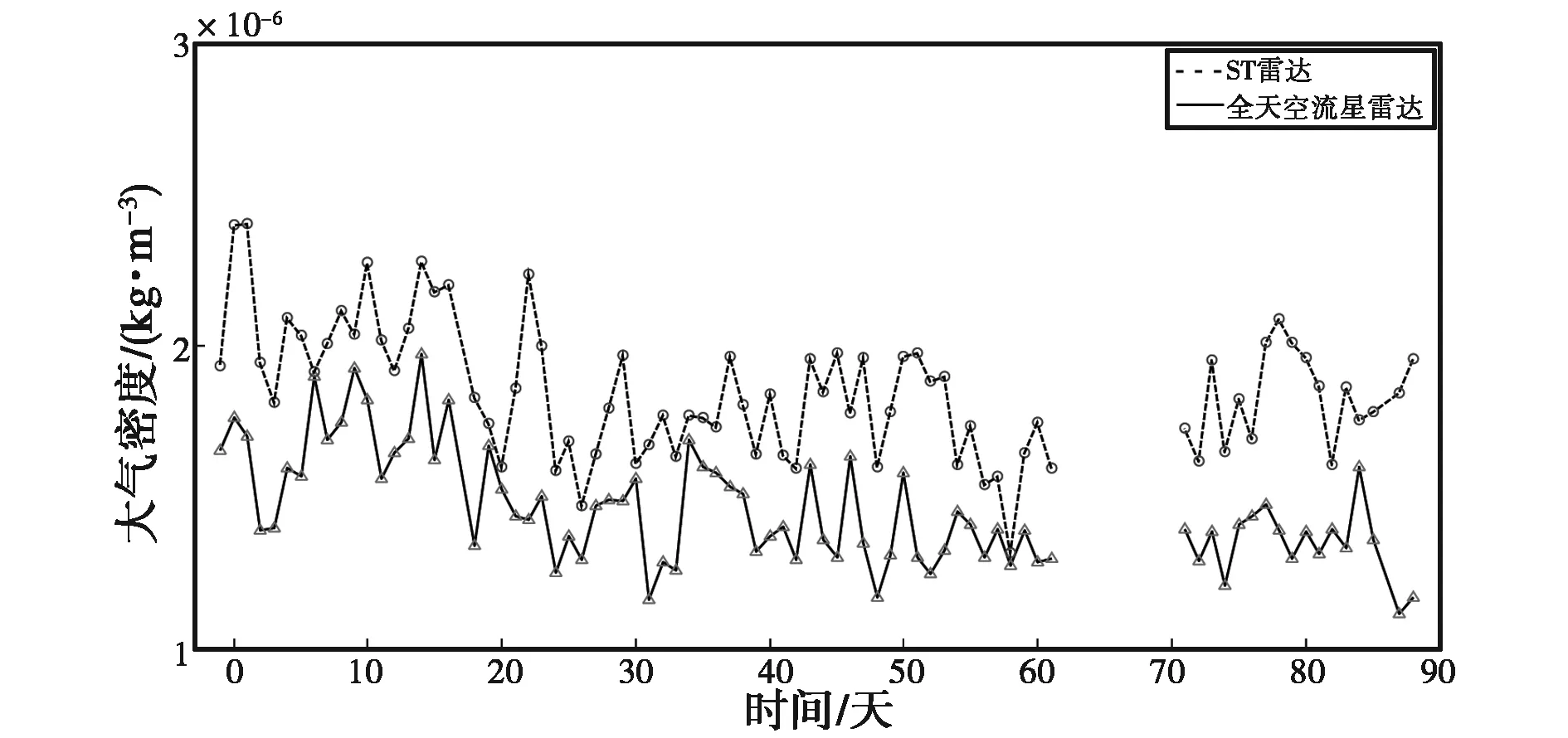
圖1～10給出了ST雷達和全天空流星雷達反演得到的大氣密度以及大氣密度差值日變化,其中ST雷達3月5日到15日缺少觀測數據．

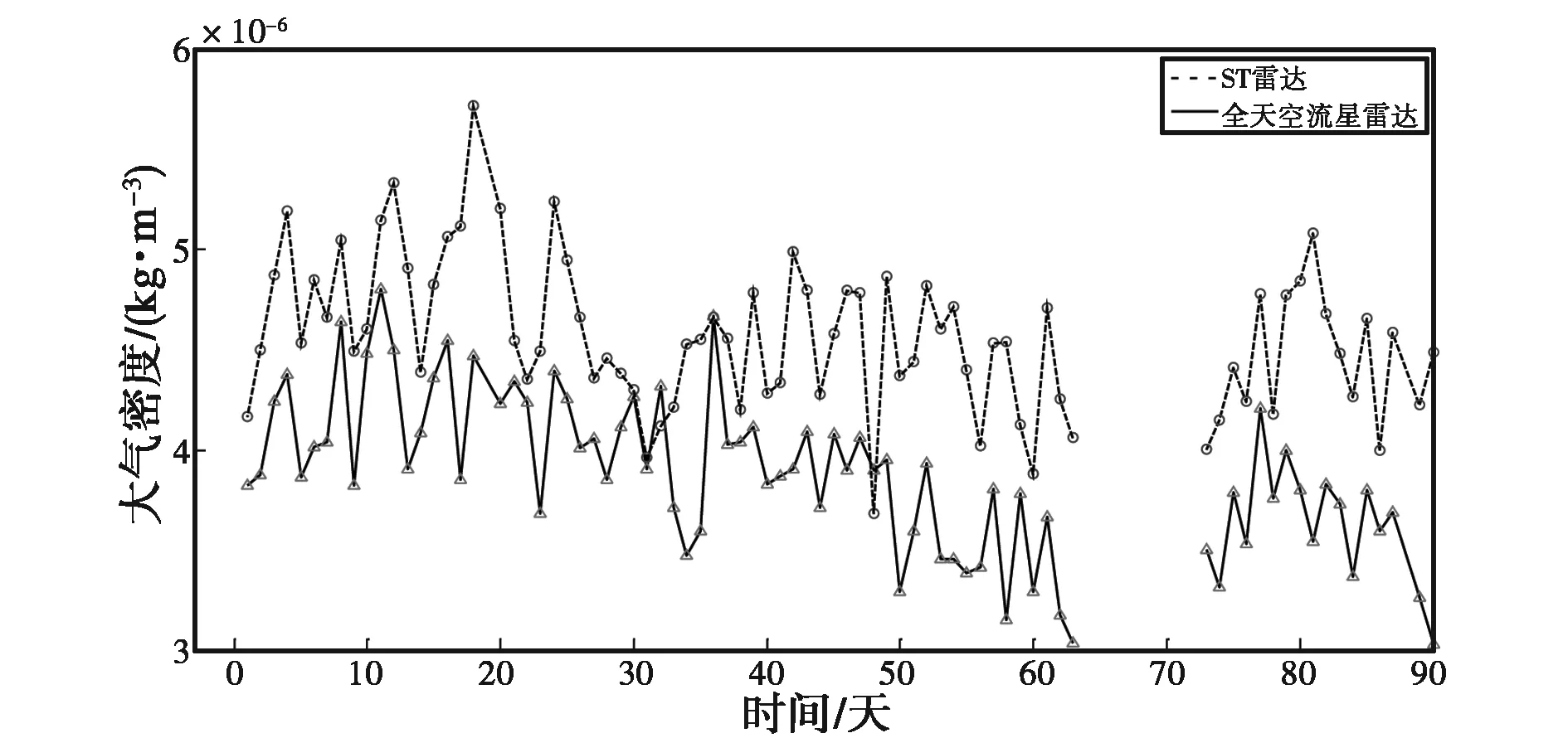
(a) 大氣密度日變化

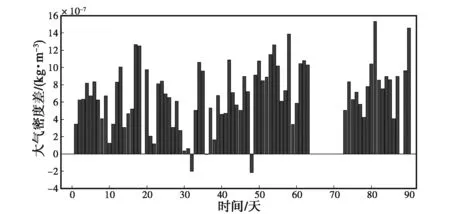
(b) 大氣密度差值日變化圖1 85 km處兩臺流星雷達得到的大氣密度及其差值日變化

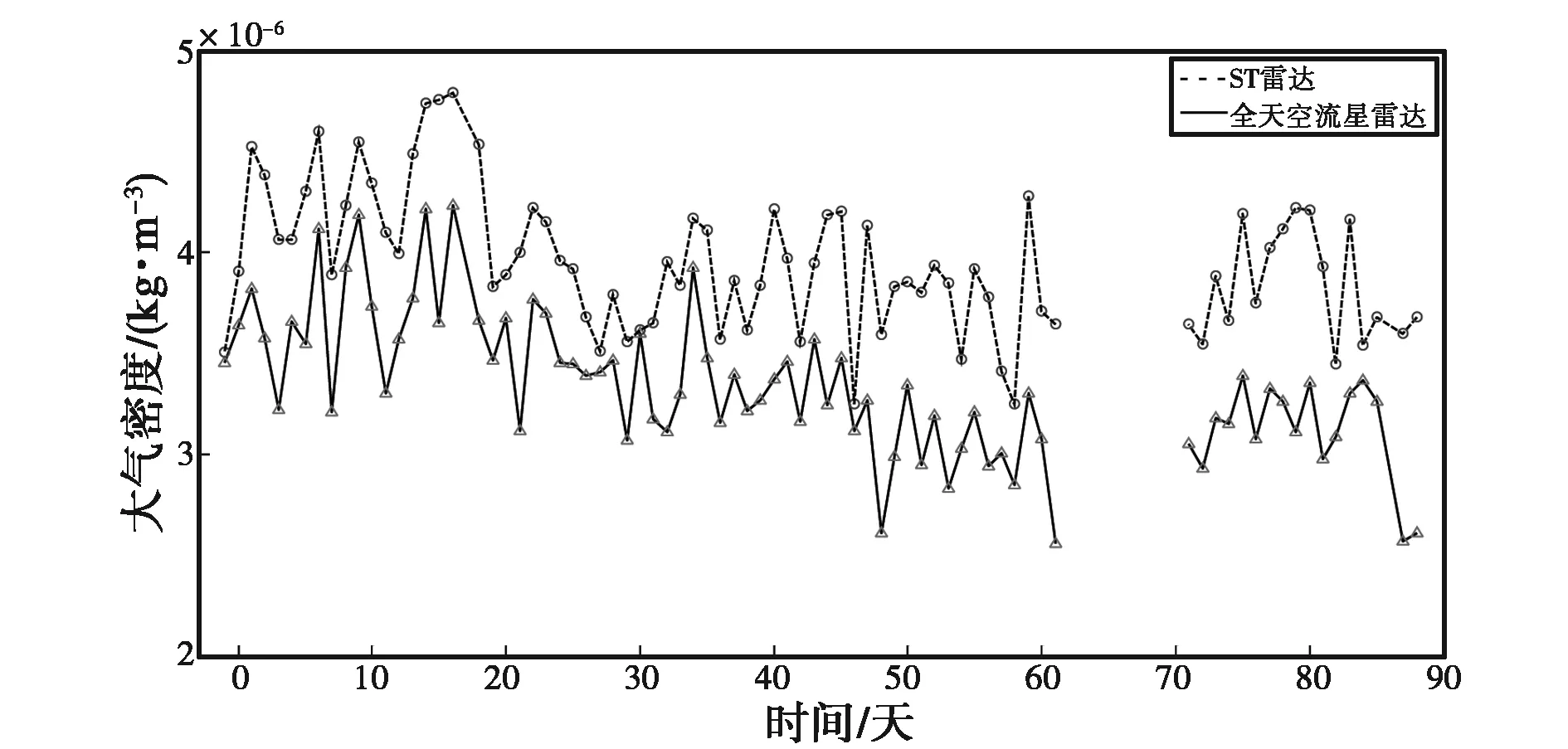
(a) 大氣密度日變化

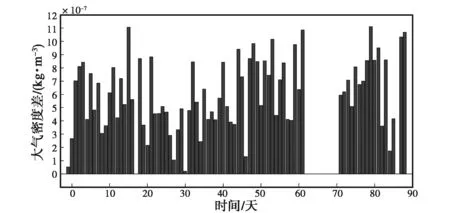
(b) 大氣密度差值日變化圖2 86 km處兩臺流星雷達得到的大氣密度及其差值日變化

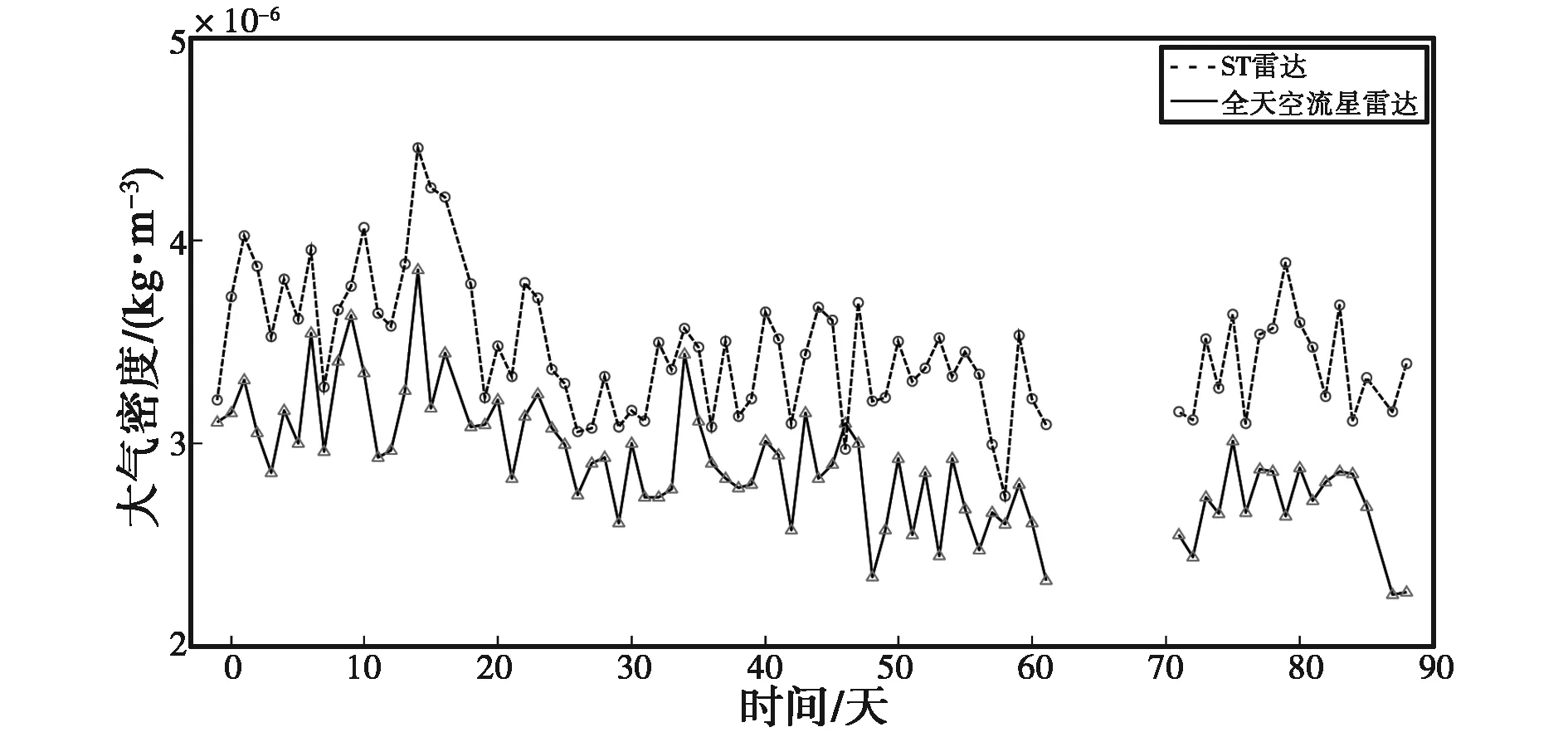
(a) 大氣密度日變化

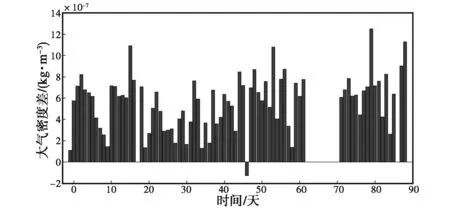
(b) 大氣密度差值日變化圖3 87 km處兩臺流星雷達得到的大氣密度及其差值日變化

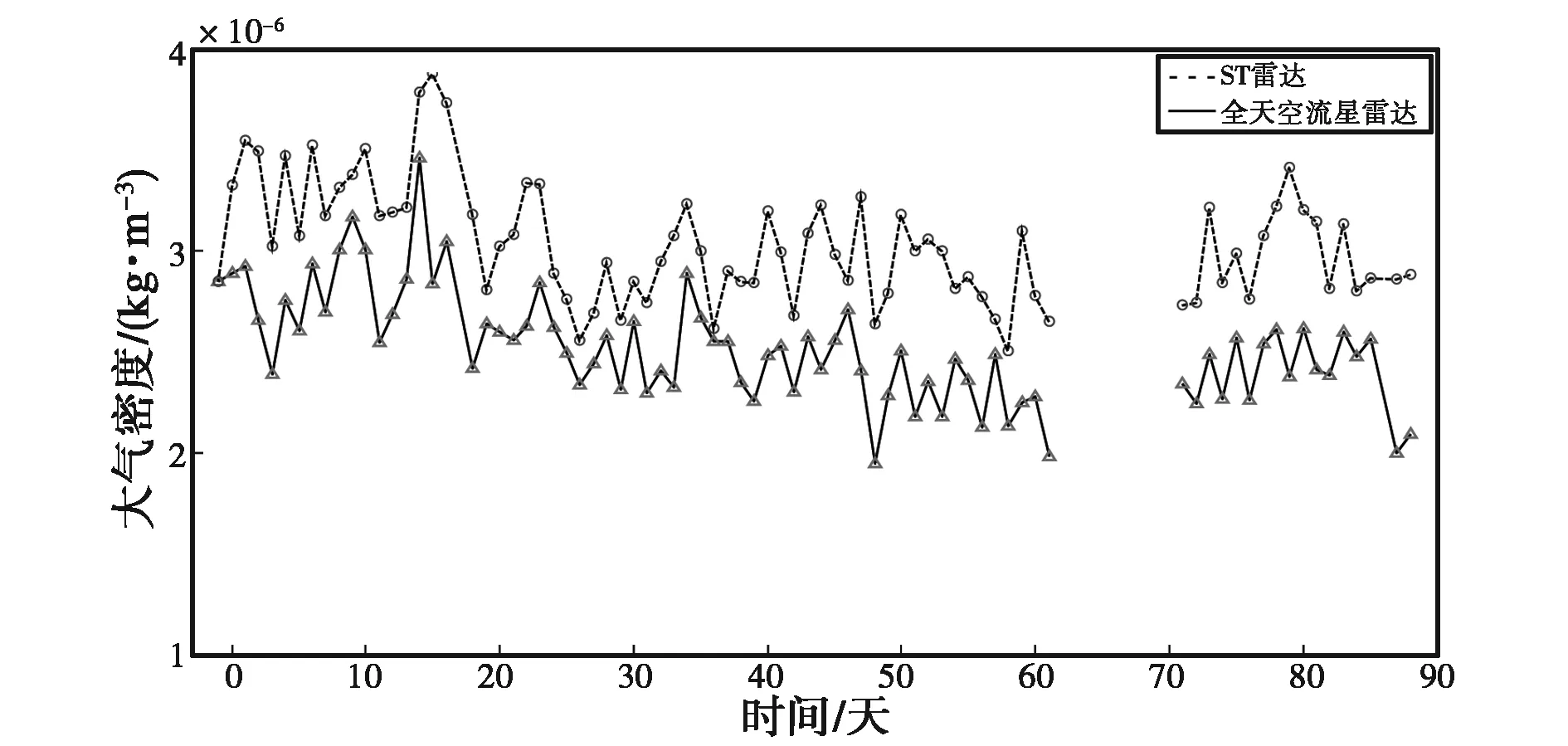
(a) 大氣密度日變化

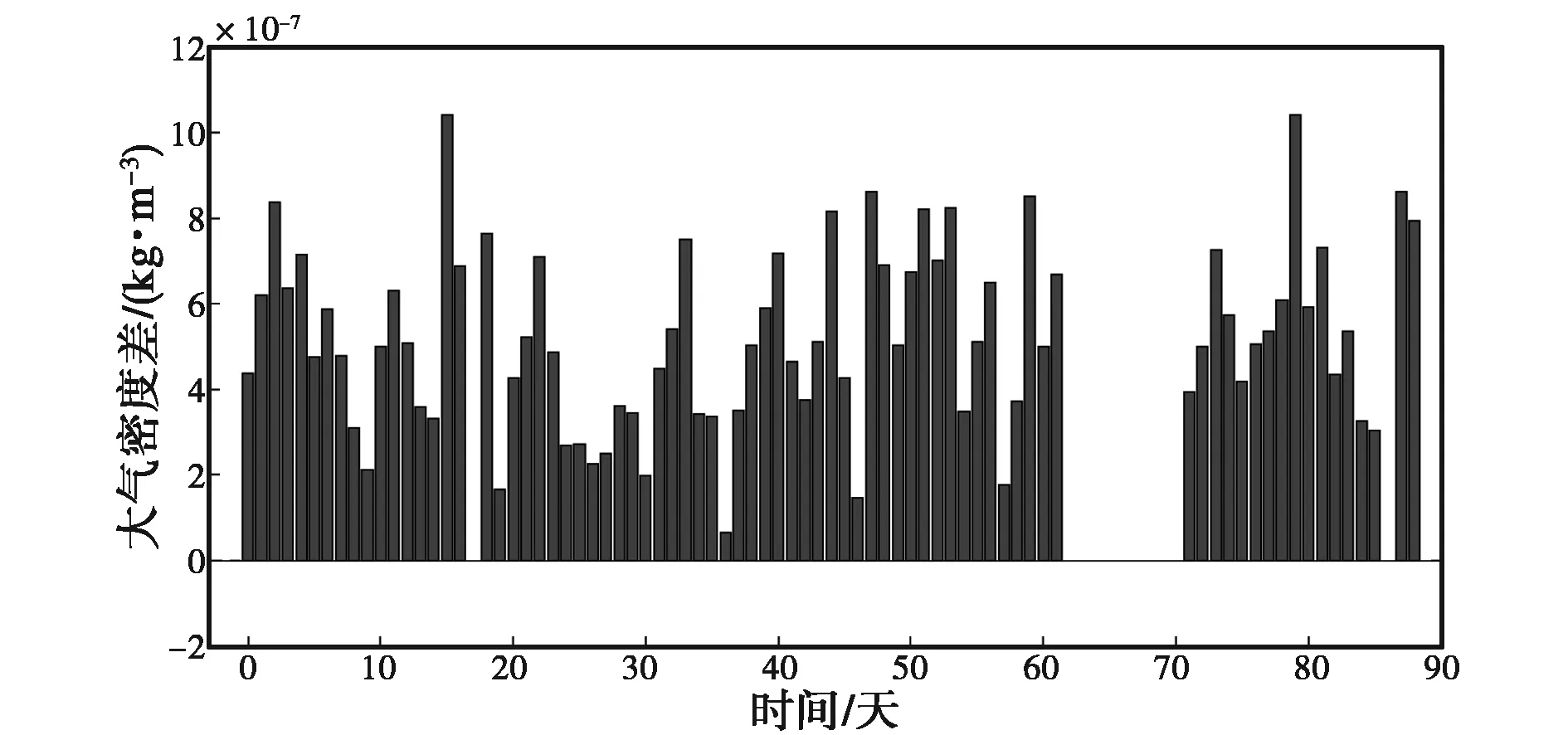
(b) 大氣密度差值日變化圖4 88 km處兩臺流星雷達得到的大氣密度及其差值日變化

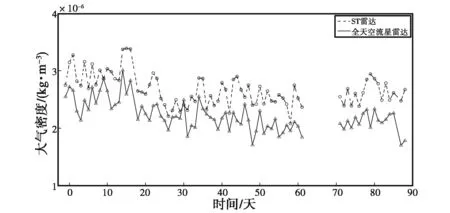
(a) 大氣密度日變化

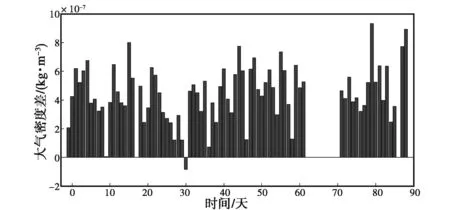
(b) 大氣密度差值日變化圖5 89 km處兩臺流星雷達得到的大氣密度及其差值日變化

(a) 大氣密度日變化

(b) 大氣密度差值日變化圖6 90 km處兩臺流星雷達得到的大氣密度及其差值日變化

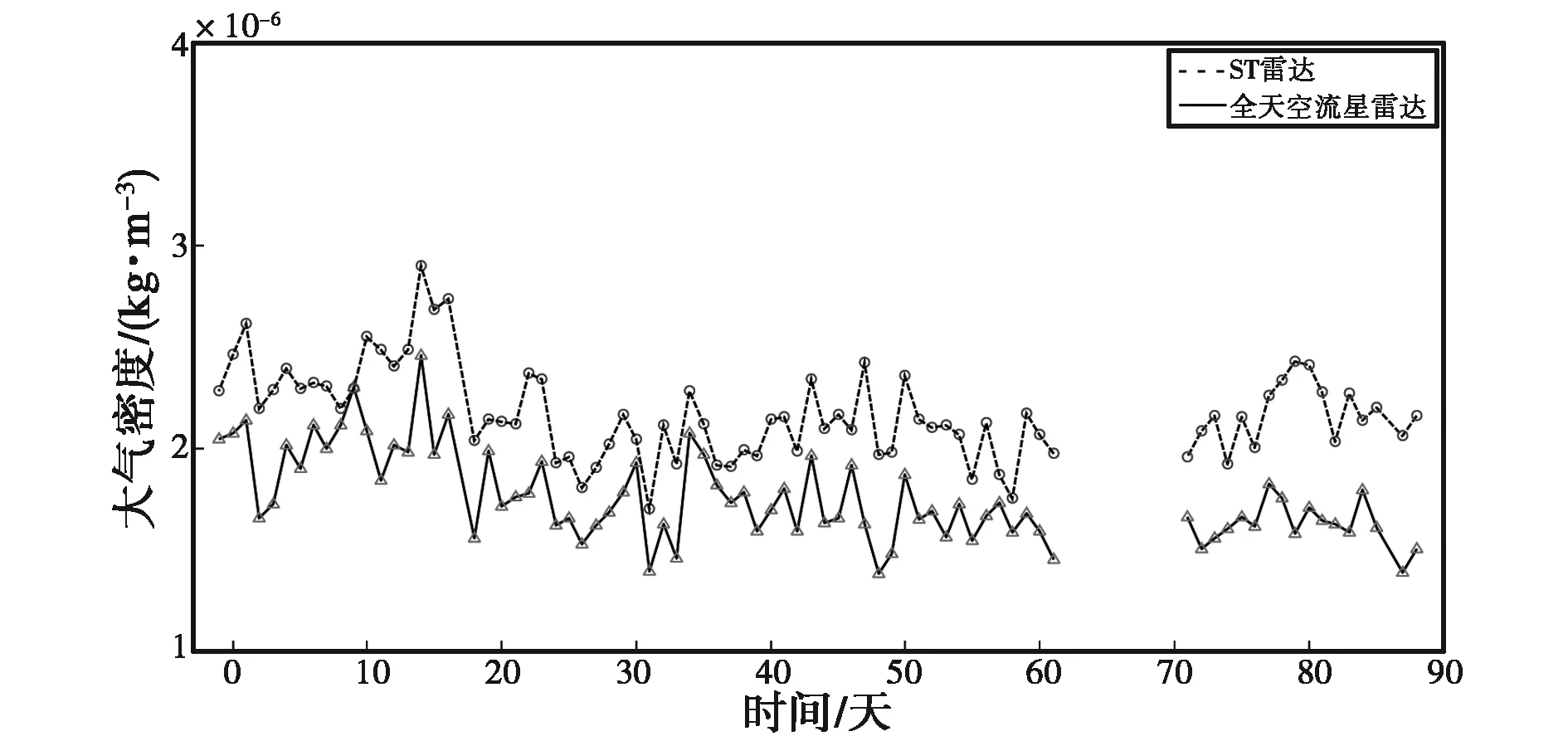
(a) 大氣密度日變化

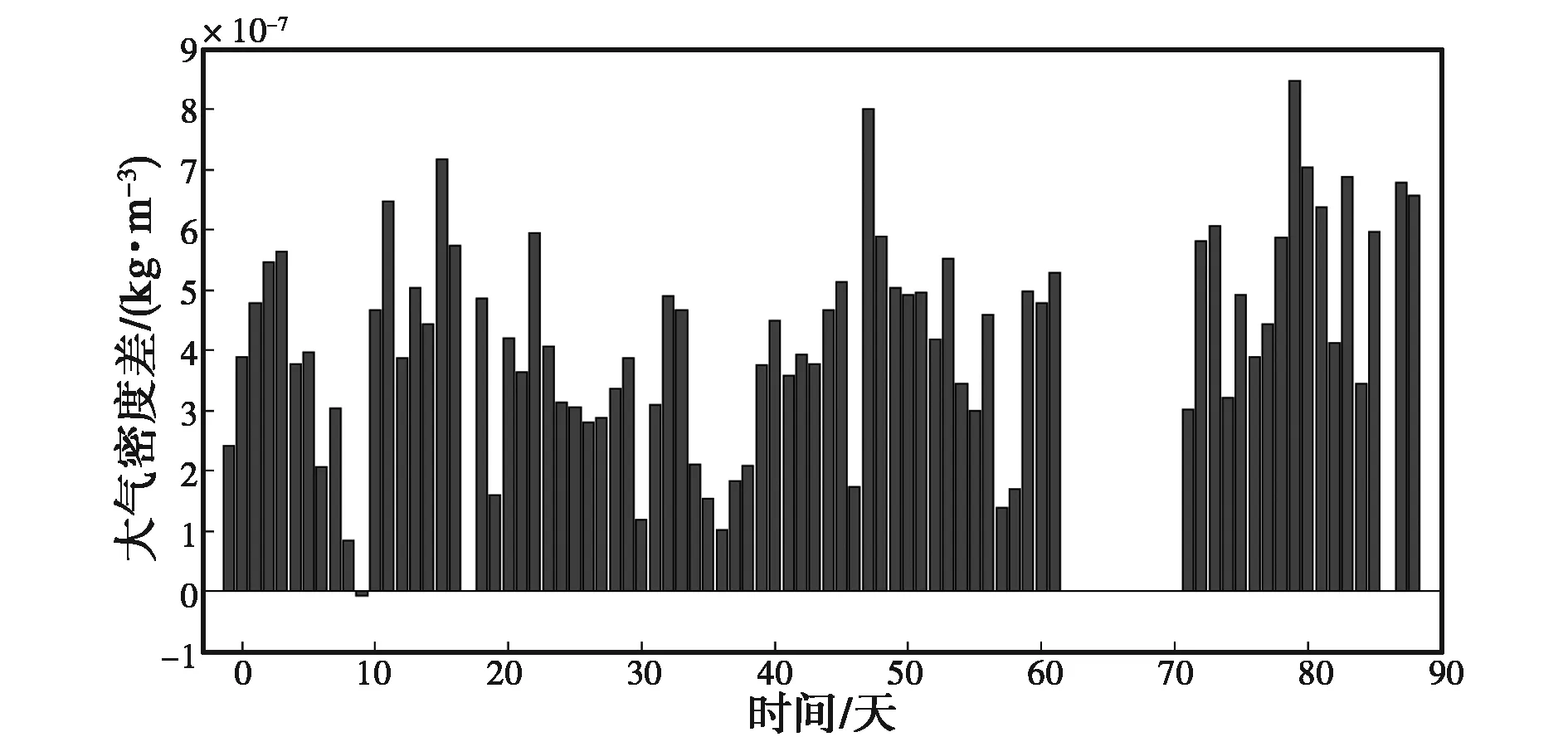
(b) 大氣密度差值日變化圖7 91 km處兩臺流星雷達得到的大氣密度及其差值日變化

(a) 大氣密度日變化

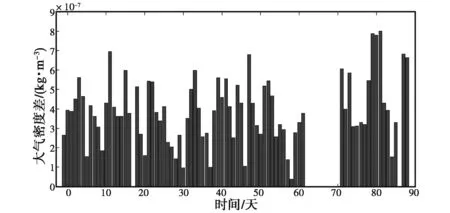
(b) 大氣密度差值日變化圖8 92 km處兩臺流星雷達得到的大氣密度及其差值日變化

(a) 大氣密度日變化

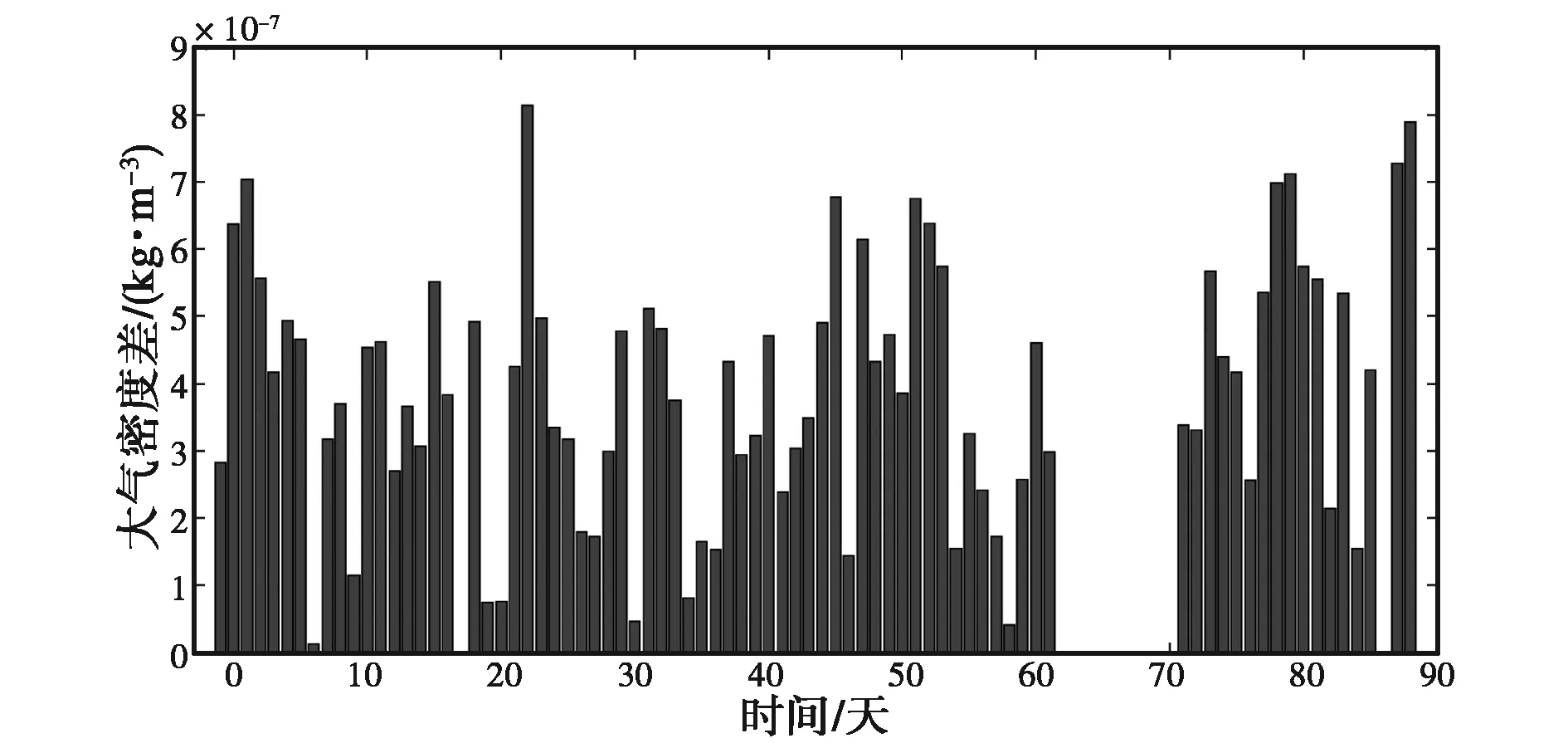
(b) 大氣密度差值日變化圖9 93 km處兩臺流星雷達得到的大氣密度及其差值日變化

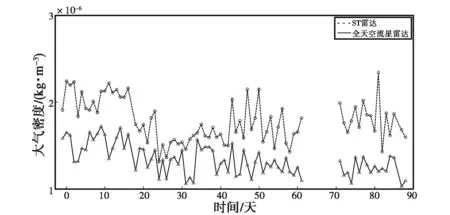
(a) 大氣密度日變化

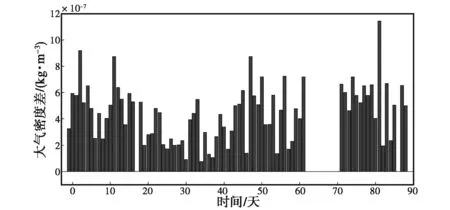
(b) 大氣密度差值日變化圖10 94 km處兩臺流星雷達得到的大氣密度及其差值日變化

由圖1～10可知:兩臺流星雷達反演出的大氣密度在各個高度上均具有較好的一致性,差值都在平均值的10%以內,整體相似度較高,但在同一高度上ST雷達得到的大氣密度值要高于全天空流星雷達．另外,計算了不同高度的大氣密度均值以及標準差,結果如表2、表3所示．

表2 全天空流星雷達反演高度剖面均值和標準差

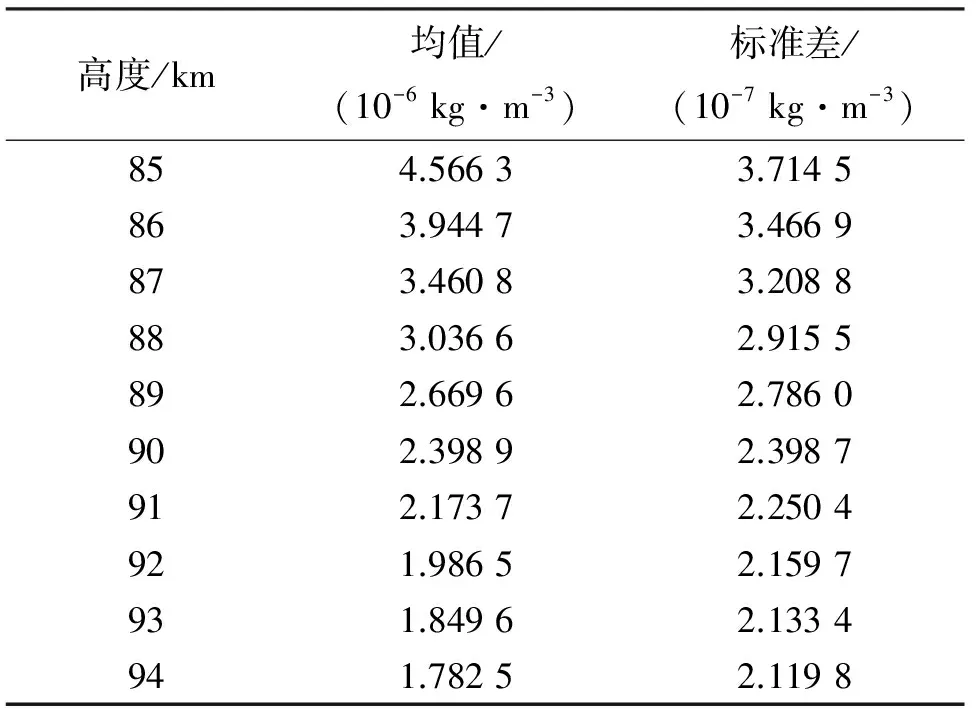
表3 ST雷達反演高度剖面均值和標準差

將表2、3中的數據通過誤差棒的形式整合,得到如圖11所示的剖面圖．

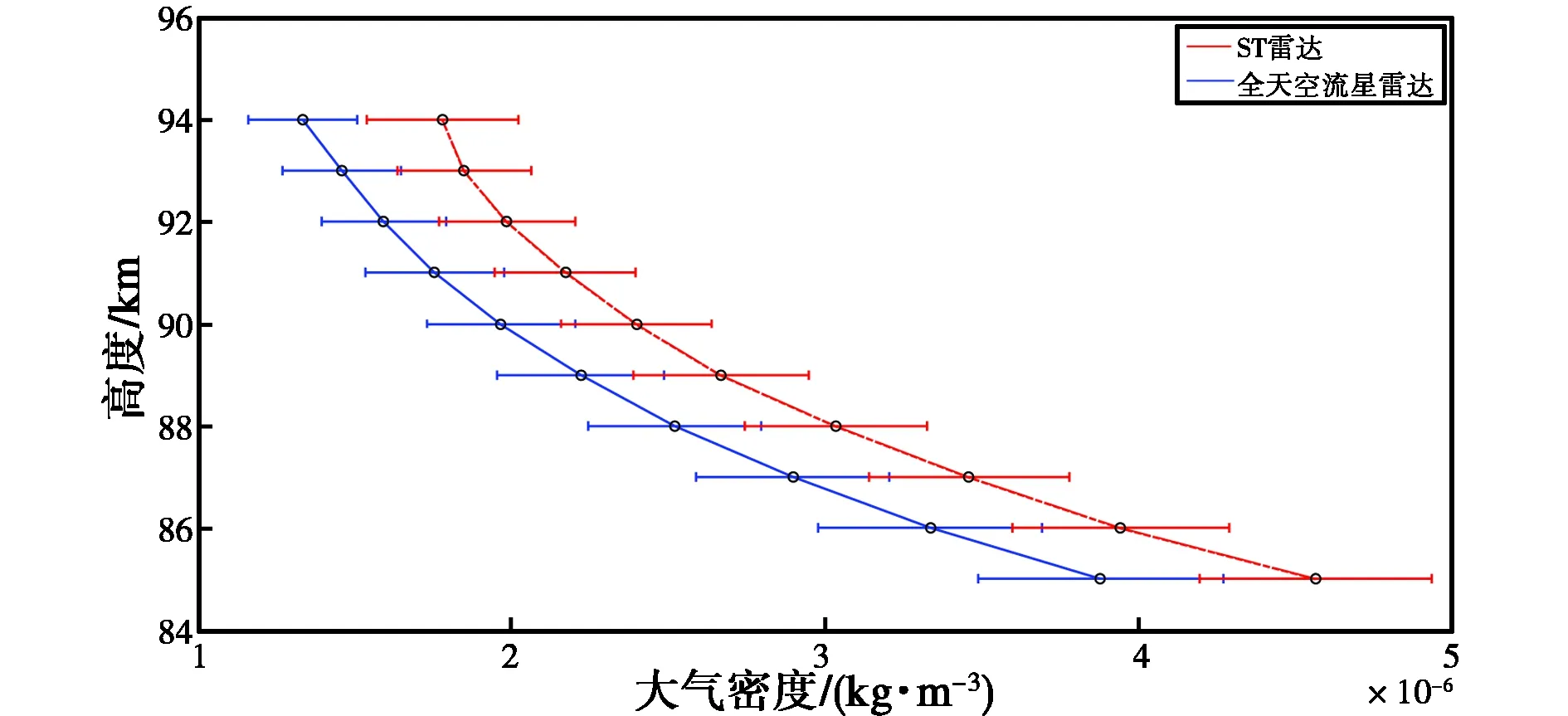
圖11 高度剖面以及大氣密度偏差

由表2、3和圖11可見:兩個雷達的高度剖面走勢曲線具有良好的一致性,且標準差的幅度均在均值的10%以內;大氣密度值較集中,可靠性較強,且隨著高度的升高,大氣密度減小的速率也逐漸變小．此外,由于峰值高度變化可以反映出大氣密度變化,圖12、13給出了兩臺雷達反演得到的大氣密度與峰值高度的走勢關系.

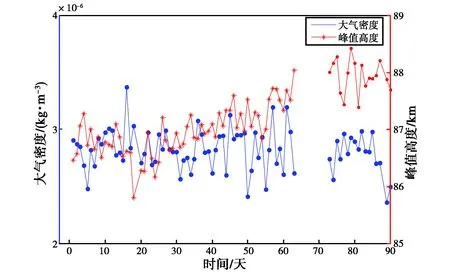
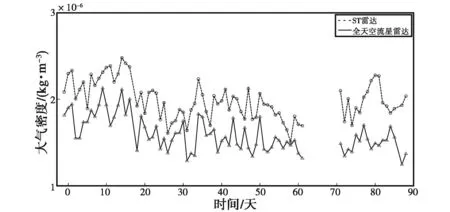
圖12 全天空流星雷達反演的峰值高度與大氣密度

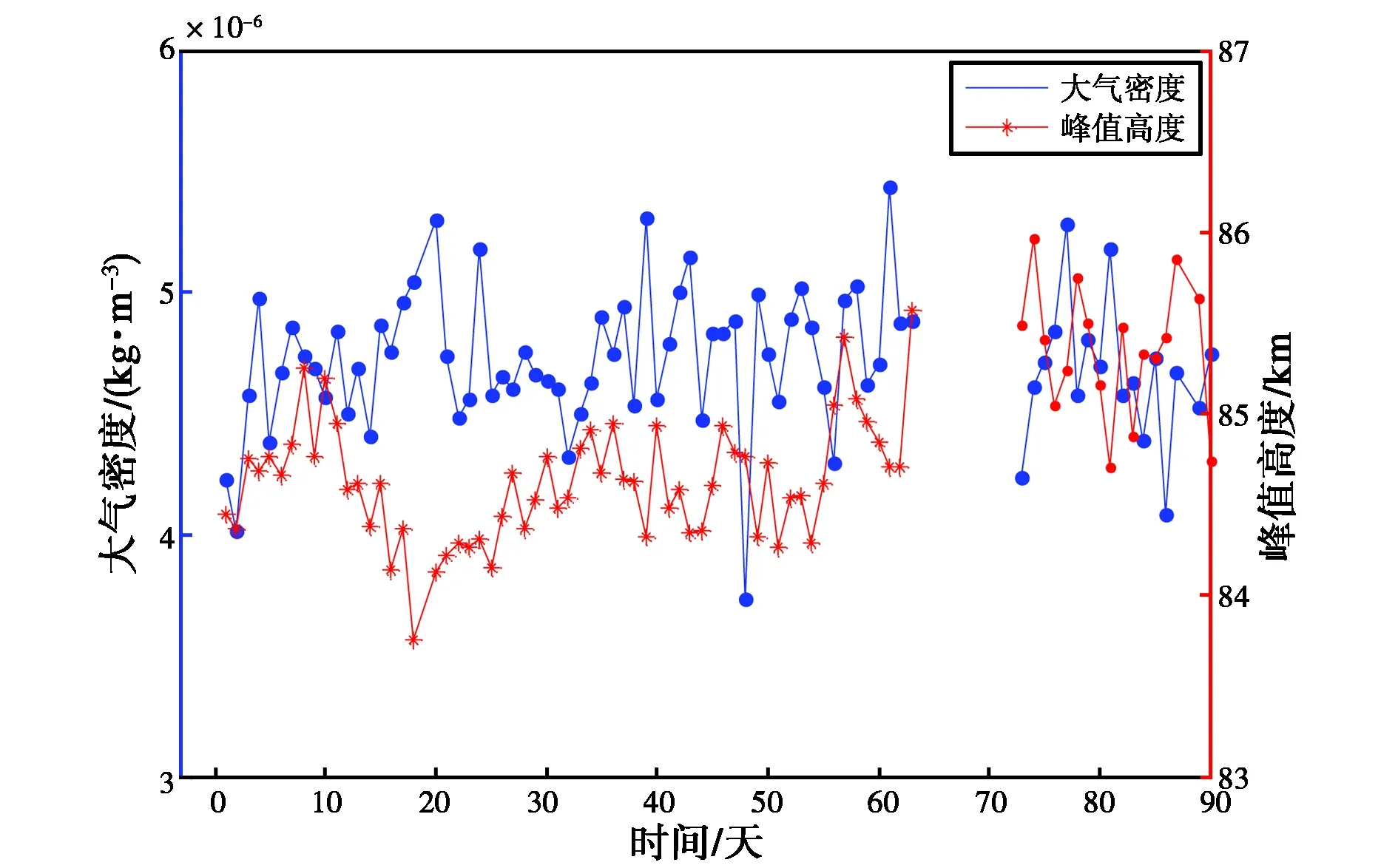
圖13 ST雷達反演的峰值高度與大氣密度

由圖12、13可以看出,除個別天數外,兩臺雷達的峰值高度與大氣密度走勢大體相似,且隔日變化一致度較高．

4 結 論

本文方法反演得到的大氣密度值與峰值檢測高度走勢大體一致,驗證了該方法的正確性．通過對比分析兩臺不同頻率雷達2014年1—3月長達90天聯合觀測得到的數據,發現兩者在對應高度上反演的大氣密度具有良好的一致性,高度剖面所呈現的偏差也在合理范圍之內．

但是由于本文方法依賴于溫度梯度公式,且溫度梯度模型在未來可能會進一步改進完善,同時所涉及數據量規模不大,季度及年變化并未給出,這也是之后所要繼續進行的研究．

流星雷達是目前探測中間層-低熱層區域大氣環境參數的強大手段,也是應用較廣泛的一套觀測系統,可以得到包括中高層大氣水平風場、中層頂大氣溫度在內的一系列參數．通過本文反演大氣密度的方法為探測中高層大氣相關參數提供了一種新的途徑．

[1] HOCKING W K, THAYAPARAN T, JONES J. Meteor decay times and their use in determining a diagnostic mesospheric temperature-pressure parameter: methodology and one year of data[J]. Geophysical research letters, 2013, 24(23): 2977-2980.

[2] STOBER G, JACOBI C, FROHLICH K, et al. Meteor radar temperatures over Collm (51.31°N, 131°E), Advance in space research, 2008, 42(7), 1253-1258.

[3] STOBER G, MATTHIAS V, BROWN P, et al. Neutral density variation from specular meteor echo observations spanning one solar cycle[J]. Geophysics research letters, 2014, 41:6919-6925.

[4] TAKAHASHI H, NAKAMURA T, TSUDA T, et al. First measurement of atmospheric density and pressure by meteor diffusion coefficient and airglow OH temperature in the mesopause region[J]. Geophysical research letters, 2001, 29(8):1165.

[5] 陳金松. 武漢流星雷達在空間環境探測中的應用研究[D]. 北京: 中國科學院, 2005.

CHEN J S. An application study of the Wuhan meter radar in space environment sounding[D]. Beijing: Chinese Academy of Sciences, 2005.(in Chinese)

[6] YI W, XUE X H, CHEN J S, et al. Estimation of mesopause temperatures at low latitudes using the Kunming meteor radar[J]. Radio science, 2016, 51 (3):130-141.

[7] HOCKING W K. Temperatures using radar-meteor decay times[J]. Geophysics research letters, 1999, 26, 3297-3300.

[8] HOLMEN S E, HALL C M, TSUTSUMI M. Neutral atmosphere temperature trends and variability at 90 km, 70°N, 19°E, 2003—2014[J]. Atmospheric chemistry & physics, 2016, 16(12):7853-7866.

[9] KUMAR K K. Temperature profiles in the MLT region using radar-meteor trail decay times: comparison with TIMED/SABER observations[J]. Geophysical research letters, 2007, 34(16):130-144.

[10] HALL C M, ASO T, TSUTSUMI M, et al. Neutral air temperatures at 90 km and 70°N and 78°N[J]. Journal of geophysical research atmospheres, 2006, 111: D14105.

[11] HALL C M, DYRLAND M E, TSUTSUMI M, et al. Temperature trends at 90 km over Svalbard, Norway (78°N l6°E), seen in one decade of meteor radar observations[J]. Journal of geophysical research atmospheres, 2012, 117(D8): 8104.

[12] NEILSEN K P, ROTTGER J, SIGERNES F. (2001), Simultaneous measurements of temperature in the upper mesosphere with an Ebert-Fastie spectrometer and a VHF meteor radar on Svalbard (78°N, 16°E)[J]. Geophysical research letters, 2001, 28(5): 943-946.

[13] HOLDSWORTH D A, MORRIS R J, MURPHY D J, et al. Antarctic mesospheric temperature estimation using the Davis mesosphere-stratosphere-troposphere radar[J]. Journal of geophysical research atmospheres, 2006, 111 (D5):1042-1063.