LC串聯電路測量液體電容率
竇如強,劉 鑫,何 鈺,杜進祥,吳 平,陳 森
(北京科技大學 a.數理學院;b.化學與生物工程學院;c.材料科學與工程學院; d.自然科學基礎實驗中心,北京 100083)

LC串聯電路測量液體電容率
竇如強a,劉 鑫a,何 鈺b,杜進祥c,吳 平a,陳 森d
(北京科技大學 a.數理學院;b.化學與生物工程學院;c.材料科學與工程學院; d.自然科學基礎實驗中心,北京 100083)
基于LC串聯電路存在“零電阻”狀態的電路特性,利用標準電感線圈和自制液體電容器,設計了可以精確測量液體電容率的實驗方法. 利用該方法測量了蒸餾水以及不同體積分數乙醇溶液的電容率,測量結果與文獻參考值的相對偏差在1%以內.
電容率;LC串聯電路;液體
電容率是反映材料極化性能的一個重要參數,它也是溶劑的重要參量,表征溶劑對溶質分子溶劑化以及隔開離子的能力[1]. 目前,對于電容率的測量主要有終端短路法[2]、波導微擾法[3-6]等,這些方法主要用于固體材料復電容率的測量,由于液體的電容率與溫度、濃度、頻率等多個物理量相關[7],應用到液體材料的測量時,對實驗設備和條件將會有更高的要求,在實驗室內完成精確測量具有一定的難度. 本文基于串聯電路存在“零電阻”狀態的電路特性,利用標準電感線圈和自制的液體電容器,提出了可以便捷、精確測量液體電容率的實驗方法.
1 實驗原理與計算方法
材料的電容率是頻率的函數,且是復數,實部反映材料容納電荷的能力,虛部反映傳導中的耗散能力. 對于液體材料而言,在大部分生化制劑及化學溶液的性質研究中,為了保證生物活性,主要關注其零頻電容率的實部,而電容率隨頻率變化的跳變點通常出現在GHz量值下[8]. 因此,在kHz,MHz甚至數十MHz下,對液體電容率的影響都可以看作是微擾,與零頻電容率相比幾乎不變. 基于上述特性,用液體材料作為電容器的填充介質,在低頻(≤1 MHz)條件下測得的電容率近似為零頻電容率. 因此本文在低頻下利用LC串聯電路的零電阻特性,設計了間接測量零頻電容率的方法. 原理如圖1所示,AC為交流信號源,R0為保護電阻,L標準電感線圈,C為自制圓柱形電容器,U為LC兩端電壓,Uo為電路輸出電壓.
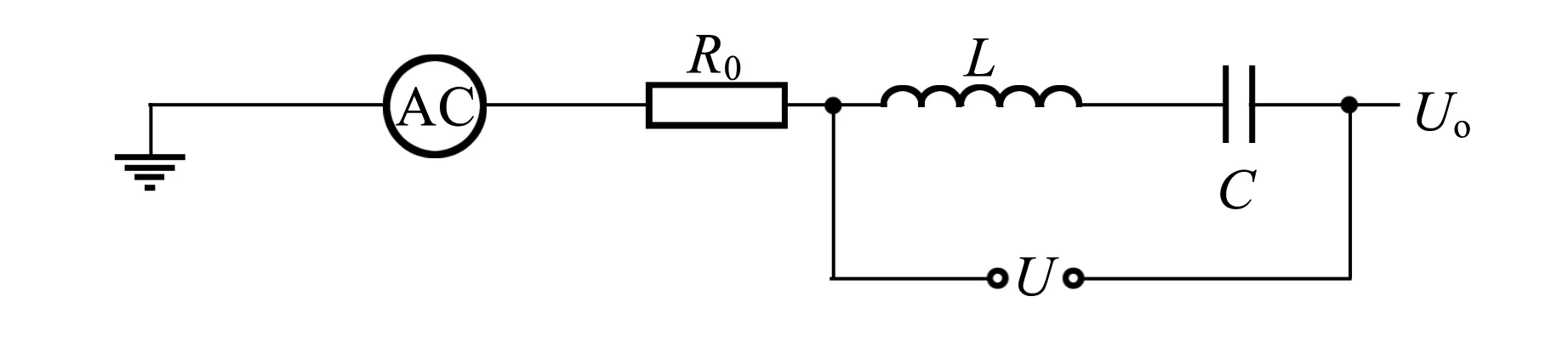
圖1 實驗原理圖
電路中輸入阻抗為

(1)
其中ω為輸入信號的圓頻率.
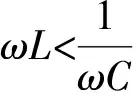
Umin=F(f0).
(2)
此時電路滿足零電阻狀態的頻率方程為
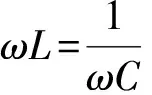
(3)
ω=2πf0.
(4)
實驗中選用圓柱形電容器,其電容值為
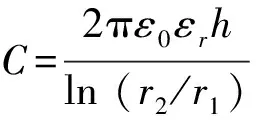
(5)
式中:εr為極間填充介質的相對電容率(零頻電容率),ε0為真空電容率,ε0=8.85×10-12F/m,h為圓柱形電容器的高度,r1為圓柱形電容器的內徑,r2為圓柱形電容器的外徑.
由式(3)~(5)可得待測電容率εr表達式為
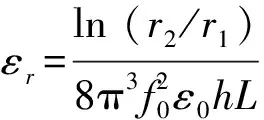
(6)
式中f0可以通過U-f曲線得到,其他量都是已知值.
2 實驗結果與討論
2.1 蒸餾水的電容率測量
實驗中所用標準電感L=1.15×10-3mH是,分別從幾個方向測量圓柱型電容器的內外徑和高度,求得平均值r1=1.2 cm,r2=4.6 cm,h=7.5 cm,利用上述方法測得的數據如表1所示.
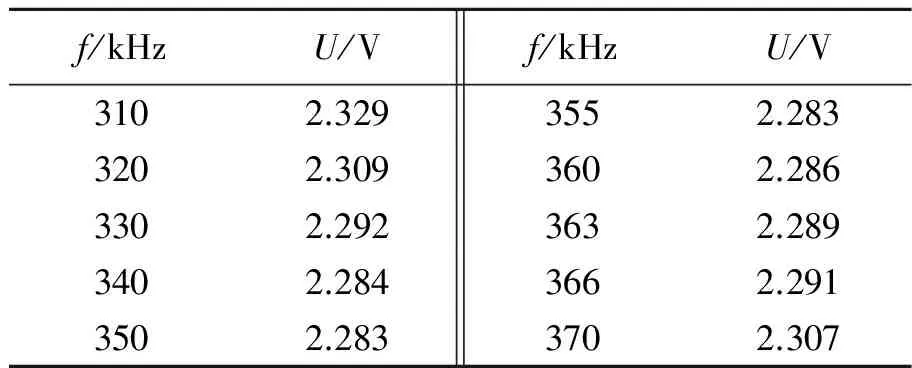
表1 LC兩端電壓U與頻率f對應關系
由表1畫出LC兩端電壓U隨輸入信號頻率f的變化關系曲線如圖2所示.
由圖2可以看出,LC兩端電壓U隨輸入信號頻率f變化先減小后增大,極小值對應的信號輸入頻率f0為352 kHz,利用式(6)可求得蒸餾水的相對電容率為78.21,與文獻參考值78.0[9]相比,相對偏差為0.27%.
2.2 不同體積分數的乙醇溶液的電容率測量
為了進一步驗證測量方法的有效性,采用同樣方法測量了不同體積分數的乙醇溶液的電容率,數據如表2所示.
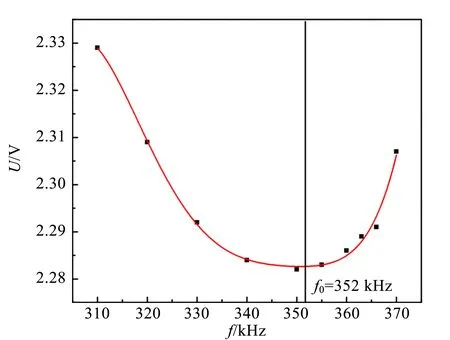
圖2 LC兩端電壓U與頻率f關系曲線
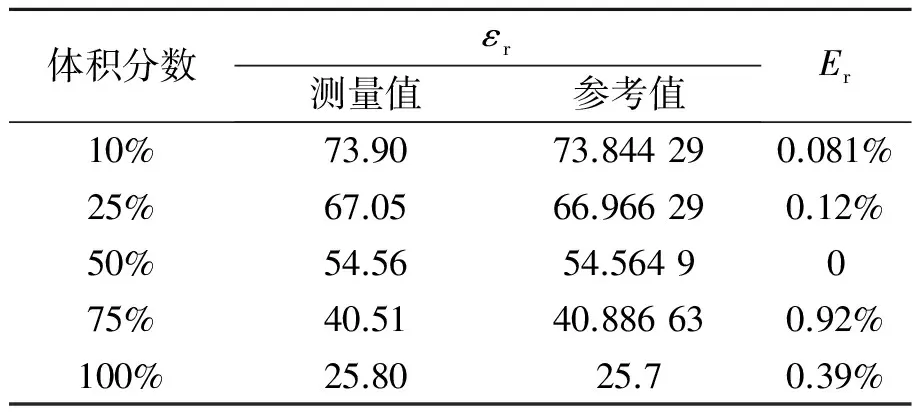
體積分數εr測量值參考值Er10%73.9073.844290.081%25%67.0566.966290.12%50%54.5654.5649075%40.5140.886630.92%100%25.8025.70.39%
由表2可看出,測得的不同體積分數乙醇溶液的電容率值與文獻參考值的相對偏差均在1%以內,利用LC串聯電路存在“零電阻”狀態的電路特性,電容值與液體電容率存在一一對應的函數關系,通過直接測量電容值可以精確、間接測量出液體的電容率,方法簡單可行.
3 結束語
通過上述實驗測量結果可以看出,基于LC串聯電路存在“零電阻”狀態的電路特性,利用標準電感線圈和自制的電容器,設計的方法不僅可以測量液體的電容率,也可以測量各種電容器的電容值,操作簡單、方便. 此外,通過測量零電阻狀態時的輸入信號頻率,可以間接計算求得電容器填充介質的電容率,減少了對直接測量數據LC兩端電壓U的使用,提高了測量精度.
[1] 李云峰,李建錫,李兵兵. 微波加熱過程中材料的復介電常數性質的研究[J]. 熱加工工藝,2012,41(12):4-6.
[2] 倪爾瑚. 用諧振腔—截止波導技術測量介質諧振器的復介電常數[J]. 微波學報,2000,19(5):554-600.
[3] 唐宗熙,張其助. 改進矩形腔微擾法測試微波電介質復介電常數[J]. 通信學報,1996,17(5):56-61.
[4] Yu K B. Accurate microwave resonant method for complex permittivity measurement of liquid [J]. IEEE Trans on MTT, 2000,48(11):2159-2164.
[5] 金浩,董樹榮. 微擾法測量介質陶瓷薄膜的介電特性[J]. 微波學報,2003,19(3):67-71.
[6] Krasezwski A W. Observations on resonant cavity Perturbation by dielectric object [J]. IEEE Trans on MTT, 1992,40(l):151-155.
[7] 金欽漢,戴樹珊,黃卡瑪. 微波化學[M]. 北京:科學出版社,1999.
[8] 鐘淑榮. 一種基于矩形波導的液體介電常數測量方法的研究[D]. 成都:四川大學,2006.
[9] 王福安,劉大壯. 二元非電介質溶液介電常數隨濃度變化的關系[J]. 鄭州工學院學報,1981(1):104-119.
[責任編輯:郭 偉]
Measuring the capacity of liquid materials using seriesLCcircuit
DOU Ru-qianga, LIU Xina, HE Yub, DU Jin-xiangc, WU Pinga, CHEN Send
(a. School of Mathematics and Physics; b. School of Chemistry and Biological Engineering;c. School of Material Science and Engineering; d. Basic Experimental Center for Natural Science,University of Science and Technology Beijing, Beijing 100083, China)
Based on the unique characteristic of seriesLCcircuit, a method was designed to measure the capacity of liquid materials, using a standard inductor and a cylinder capacitor. Using the above method, the capacity of distilled water and alcohol solution was measured. The relative error between the measured result and the reference value was less than 1%.
capacity; seriesLCcircuit; liquid materials
2016-05-29
北京科技大學研究型教學示范課建設項目(No.KC2014YJX30)
竇如強(1993-),男,河北承德人,北京科技大學數理學院黃昆班2013級本科生.
指導教師:陳 森(1978-),男,河南濮陽人,北京科技大學物理實驗中心高級工程師,碩士,主要從事物理實驗教學工作.
O441.1
A
1005-4642(2017)02-0046-03
“第9屆全國高等學校物理實驗教學研討會”論文

