電磁場下顆粒阻尼動態特性試驗研究

胡 溧, 涂 迪， 楊啟梁， 徐 賢

(1.武漢科技大學 汽車與交通工程學院，武漢 430081; 2.東風商用車有限公司 技術中心，武漢 430056)

電磁場下顆粒阻尼動態特性試驗研究

胡 溧1, 涂 迪1， 楊啟梁1， 徐 賢2

(1.武漢科技大學 汽車與交通工程學院，武漢 430081; 2.東風商用車有限公司 技術中心，武漢 430056)

利用穩態能量流法對直流電磁場作用下顆粒阻尼器的阻尼特性進行了試驗研究。試驗結果表明：在一定振動情況下，通過施加直流電磁場的方法，可以改變顆粒阻尼器阻尼性能;在較低振動加速度幅值(<32.5 m/s2)下，顆粒體產生的損耗功率和損耗因子隨電流強度的增強而減小；當振動加速度增大到32.5 m/s2后，損耗功率和損耗因子會隨電流強度的增強而增大。阻尼顆粒的有效質量隨激勵幅值的增加呈先平緩再降低的趨勢，且電流強度的變化對有效質量影響較小。

電磁顆粒阻尼器；損耗功率；損耗因子；有效質量

非阻塞性顆粒阻尼(Non Obstructive Particle Damping，NOPD)技術指將金屬或非金屬顆粒物質按某一填充率放入振動結構的空腔內，結構在振動過程中，通過顆粒物質之間以及顆粒物質與空腔壁間的碰撞和摩擦，將機械能轉化為熱能和聲能，從而耗散振動主結構的能量，產生阻尼效應的振動被動控制技術。非阻塞性顆粒阻尼具有減振頻帶寬，噪聲小，對原始結構改變較小等優點[1]。影響顆粒阻尼特性的因素有很多，如容器填充率、顆粒粒徑大小、顆粒的材料屬性等。胡溧等[2]建立了顆粒阻尼的粉體力學模型，對顆粒阻尼器容器形狀、尺寸對顆粒阻尼特性的影響進行了研究。

在較低振動強度下，摩擦是阻尼顆粒產生能量損耗的主要原因[3]。而影響阻尼顆粒摩擦耗能的因素有兩個，一個是顆粒間以及顆粒與容器壁間的摩擦因數，對于阻尼顆粒的材料、形狀和尺寸已經確定的顆粒阻尼器而言，摩擦因數也確定不變；另外一個因素為顆粒體之間的壓力大小，當顆粒間具有相對摩擦時，顆粒體間壓力越大摩擦力就越大，同樣振動水平下損耗能量越大。因此，如何改變顆粒體的受力來提高阻尼器性能成為研究的問題。

SHAH等[4]提出了將阻尼顆粒置于電磁場中的方案，研究電磁場對阻尼顆粒減振性能的影響。本文受此啟發將普通顆粒阻尼器改造成鐵磁顆粒阻尼器。通過試驗對該型阻尼器在電磁場作用下動態特性進行研究，得到顆粒阻尼器的阻尼特性隨加電流強度變化的規律。

1 實驗裝置及測量系統

將直徑0.7 mm碳鋼顆粒裝入高為6 cm，內徑為2.5 cm的不銹鋼圓柱容器(m=30 g)內。保證顆粒填充率為70%，此時碳鋼顆粒和容器質量和為100 g。然后采用外繞線圈的方法，在圓柱容器外表面均勻緊密繞400匝銅線圈，將普通顆粒阻尼器改造成電磁顆粒阻尼器，如圖1所示。

圖1 阻尼顆粒與電磁顆粒阻尼器Fig.1 Damping particle and electromagnetic particle damper

實驗采用LMS公司的振動測試系統(見圖2)完成信號的采集、處理以及對激振器的閉環控制。電磁顆粒阻尼器下方的加速度信號和力信號傳送到信號采集分析系統，同時內置信號發生器對該加速度信號進行反饋控制，實現激振器以確定的加速度和頻率對電磁顆粒阻尼器的進行激勵。直流電源和滑線變阻器用來控制電磁顆粒阻尼器線圈中的電流強度大小。

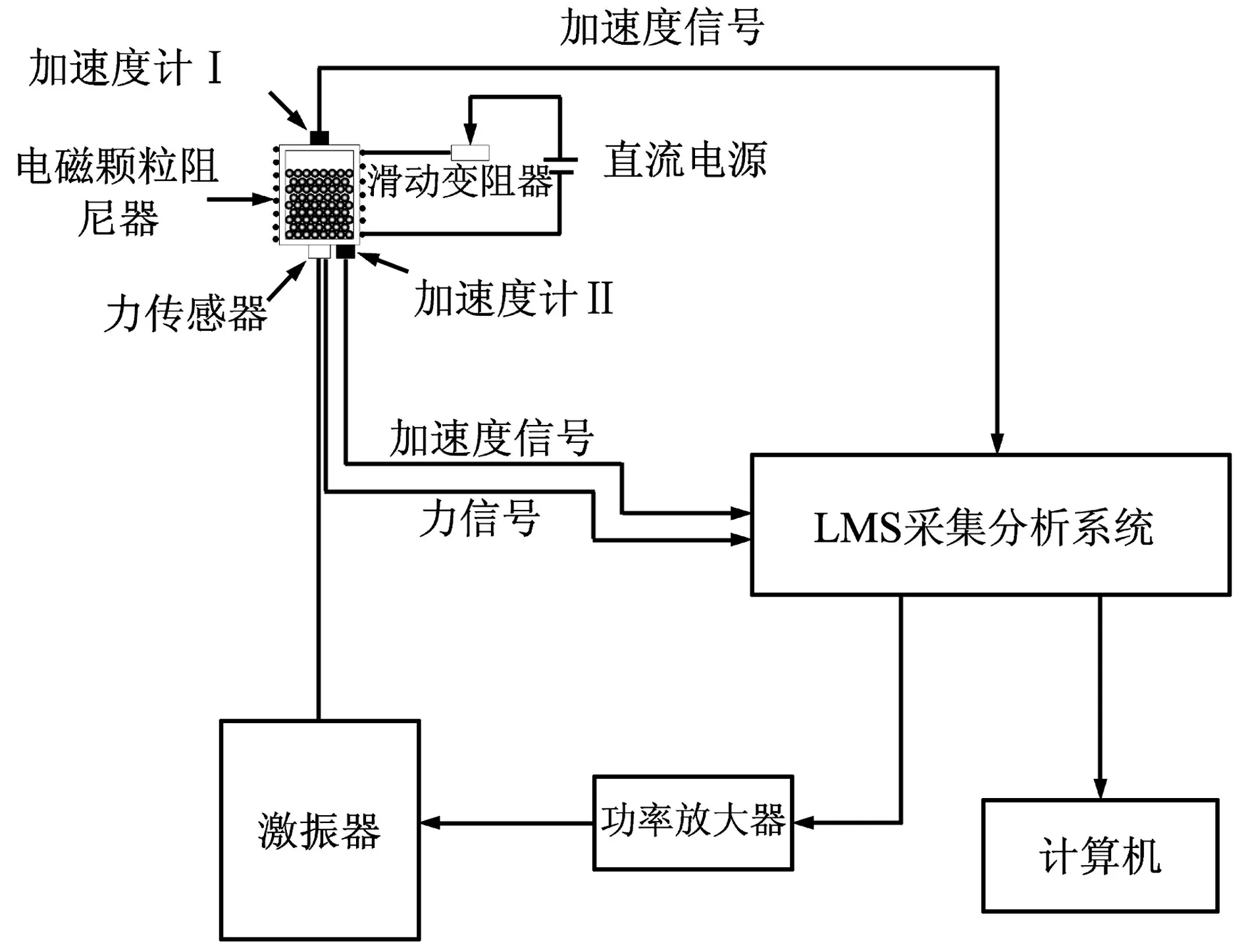
圖2 試驗測試系統示意圖Fig.2 Test system schematic diagram

2 穩態能量流法計算損耗功率、損耗因子及等效質量的原理

由振動力學可知，在穩態有阻尼受迫振動系統中，阻尼消耗的能量等價于激振力所做的功。因此，計算損耗功率(或損耗因子)可以通過測量系統的輸入功率來確定[5]。試驗中系統的輸入和輸出分別為力傳感器的力信號與加速度計Ⅰ的加速度信號。通過對采集的信號進行處理，得到力、加速度的幅值以及相位差值。

對于系統的輸入功率Pin可以表示

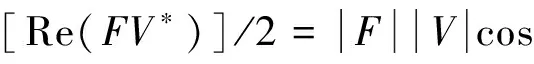
(1)

式中:Rfv、Sfv為力信號與加速度信號之間的互相關和互譜；f(t)、v(t)分別為力和速度信號的時間歷程；為時間平均；F和V分別為f(t)、v(t)的復幅值；V*為V的共軛復數量；(φF-φV)為力與速度之間的相位差。

對于穩態振動，損耗功率與系統的輸入功率相等

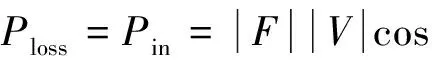
(2)

利用無功功率和結構動能之間的時間微分關系，求得結構體動態質量m[6]

(3)

(4)

式中:Im(Pin)為輸入復功率的虛部(無功功率);A為加速度信號的復幅值;i為虛數單位。

內部損耗因子可由下式計算得到

(5)

(6)

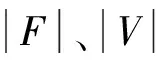
將式(3)、式(4)和式(6)代入式(5)中可以得到

(7)

3 鐵磁顆粒體在電磁場作用下的受力分析及摩擦特性

3.1 鐵磁顆粒體在電磁場作用下的受力分析

鐵磁顆粒體受磁場作用后，每個顆粒體會感應出固定大小的磁矩。顆粒體感應磁矩與磁感應強度成正比關系。作用在磁顆粒體上的力包括磁場對磁顆粒體的作用力和磁粒體之間通過磁偶極相互作用兩部分。

本文設計的顆粒阻尼器，可以看成通電螺線管，此時由安培定理可以求出阻尼器內磁場磁感應強度B

(8)

式中:μ0為真空磁導率;H為磁場強度;N為通電螺線管線圈匝數;n為單位長度上線圈匝數;l為通電螺線管管長。由式(8)可知，當電磁顆粒阻尼器施加的電流為定值時，此時電磁場為均勻恒定磁場。

3.1.1 電磁場對磁顆粒體的作用力

電磁場對磁顆粒體的作用力可表示為[7]

Fm=(m·B)=(m·)B=mB

(9)

式中:m為顆粒體感應磁矩;B為磁感應強度;m·B為磁矩與磁感應強度的點積;為標量場的梯度。

由式(9)可得磁顆粒體受力方向為磁場梯度方向， 力大小與磁場梯度成正比。但當磁場為均勻磁場時，磁場梯度為零, 磁顆粒體不受磁場作用力。

3.1.2 顆粒體間的相互作用力

由于顆粒體直徑較小(0.7 mm)，可以將每個顆粒體視為單獨的磁偶極子。顆粒體間的相互作用力可以用磁偶極子間的磁偶極-偶極作用來描述[8]。對于磁矩為m的磁偶極子與另一磁偶極子m′之間的磁作用力可以分為

當兩個磁偶極子共軸平行時，其相互作用力為

(10)

當兩個磁偶極子在垂直線上平行時，其相互作用力為

(11)

當兩個磁偶極子與連線成45°角平行時，其相互作用力為

(12)

由式(10)、式(12)可知，在恒定電磁場的作用下，圓柱形容器內不同層面的顆粒間的磁偶極作用力是吸引力。式(11)表示在同一水平層面內顆粒間的磁偶極作用力為排斥力，雖然在水平方向上會降低顆粒間的接觸力，但顆粒體與容器壁間的接觸力會加大,此時水平排斥力對顆粒阻尼性能的影響較小[9]。

上述分析得到，顆粒體只受到磁偶極作用力且與磁矩平方成正比。由于顆粒體感應磁矩大小與磁感應強度成正比，而磁感應強度與通電螺線管內電流成正比，那么線圈中的電流大小決定了磁顆粒間作用力強弱。

3.2 非阻塞性顆粒阻尼摩擦特性

毛寬民等[10]研究了非阻塞性顆粒阻尼結構的摩擦特性。其中顆粒切向接觸力可表達為

Ft=(-Ktδt-Cetνt)

(13)

顆粒間法向接觸力可表示為

Fn=(-Knδn-Cenνn)

(14)

顆粒間摩擦力表示為

(15)

式中:μf為動摩擦因數；Cet為切向接觸阻尼系數；δt和νt分別為切向疊合量和切向速度；Cen為法向接觸阻尼系數；δn和νn分別為法向疊合量和法向速度。

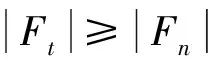
(16)

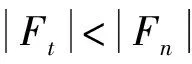
4 損耗因子、損耗功率和有效質量試驗測試及結果分析

為了研究電磁場下顆粒阻尼的損耗因子、損耗功率和有效質量，按試驗裝置圖(見圖3)連接好裝置進行試驗。加速度幅值變化區間為10～55 m/s2，幅值間隔2.5 m/s2；頻率變化區間為20～160 Hz，頻率間隔為10 Hz；電流變化區間為0～1.5 A，電流間隔為0.3 A。通過對所得數據進行處理后，由式(2)計算出損耗功率；由式(3)計算出阻尼器有效動質量；由式(7)計算出阻尼器的損耗因子。最后通過曲面擬合法得到不同電流強度下損耗功率、損耗因子以及有效質量關于頻率和加速度幅值的三維曲面圖。

圖3 試驗裝置示意圖 Fig.3 The installation of experimental system

4.1 顆粒阻尼損耗因子

損耗因子是衡量系統的阻尼特性并決定其振動能量耗散能力的重要參數，也稱為阻尼損耗因子[11]。通過計算得到的阻尼損耗因子反映了阻尼器耗能能力，是評價其耗能性能的指標。

運用Matlab軟件對所得數據進行三維曲面擬合，得到0～1.5 A，不同電流強度下損耗因子隨頻率及加速度幅值變化的三維曲面圖。選取電流I=0 A和I=1.5 A時三維曲面圖，分別如圖4所示。

由圖4可知，顆粒阻尼損耗因子對應加速度幅值、頻率的三維曲面呈山脊型形狀分布。當頻率一定時，損耗因子隨加速度的增大先快速增大，而后緩慢下降。這是因為振動加速度較小時，容器內的顆粒未能充分運動，此時耗能能力較差；當振動加速度增大到一定值時(大約為32.5 m/s2)，容器內顆粒充分運動，顆粒間以及顆粒與容器壁間摩擦、碰撞耗散較多能量，此時顆粒阻尼器耗能能力達到最大；而振動加速度繼續增大時，部分顆粒還沒獲得某一方向足夠的動能即隨阻尼器改變運動方向，導致摩擦和碰撞減弱，顆粒損耗因子隨激勵幅值增加而減小。

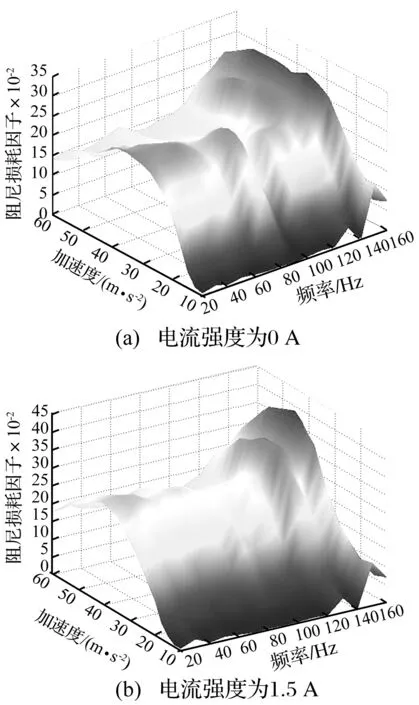
圖4 損耗因子三維曲面圖Fig.4 Loss factor three-dimensional surface diagram

選取頻率(f=40 Hz、80 Hz)對損耗因子三維曲面圖進行截取，得到不同電流強度下損耗因子隨加速度變化曲線圖(見圖5)。由圖5可知，振動加速度幅值較小時(<32.5 m/s2)，損耗因子隨電流強度的增加而減小。因為振動強度低，顆粒之間無相對運動。此時增大電流，由式(8)可知，阻尼器內磁感應強度增大。而顆粒體感應磁矩與磁感應強度成正比，那么顆粒體感應磁矩m會變大。由磁偶極作用力計算式(10)和式(12)得，顆粒間的吸引力作用會隨感應磁矩的變大而增強，顆粒法向接觸力相應變大。此時顆粒更不易發生相對運動，阻尼顆粒摩擦耗能能力減弱。當振動幅值增大到一定值后，損耗因子會隨電流強度的增加而增大。這是因為振動強度增大后，顆粒充分運動。顆粒間由于摩擦，會消耗能量。此時增大電流，顆粒間法向接觸力隨電流的增大而變大，由式(15)、式(16)知，顆粒間摩擦力變大，阻尼顆粒摩擦耗能能力增強。

同時由圖5可知，在相同振動強度下，施加的電流大小差值越大，阻尼器損耗因子變化越明顯。其中電流分別為0 A和1.5 A下阻尼器損耗因子對比如表1所示。可以看出，較低振動強度下，施加電流使得阻尼器損耗因子可減小約30%～40%；當振動強度增大到一定值，施加電流后，損耗因子可增大約20%～30%。

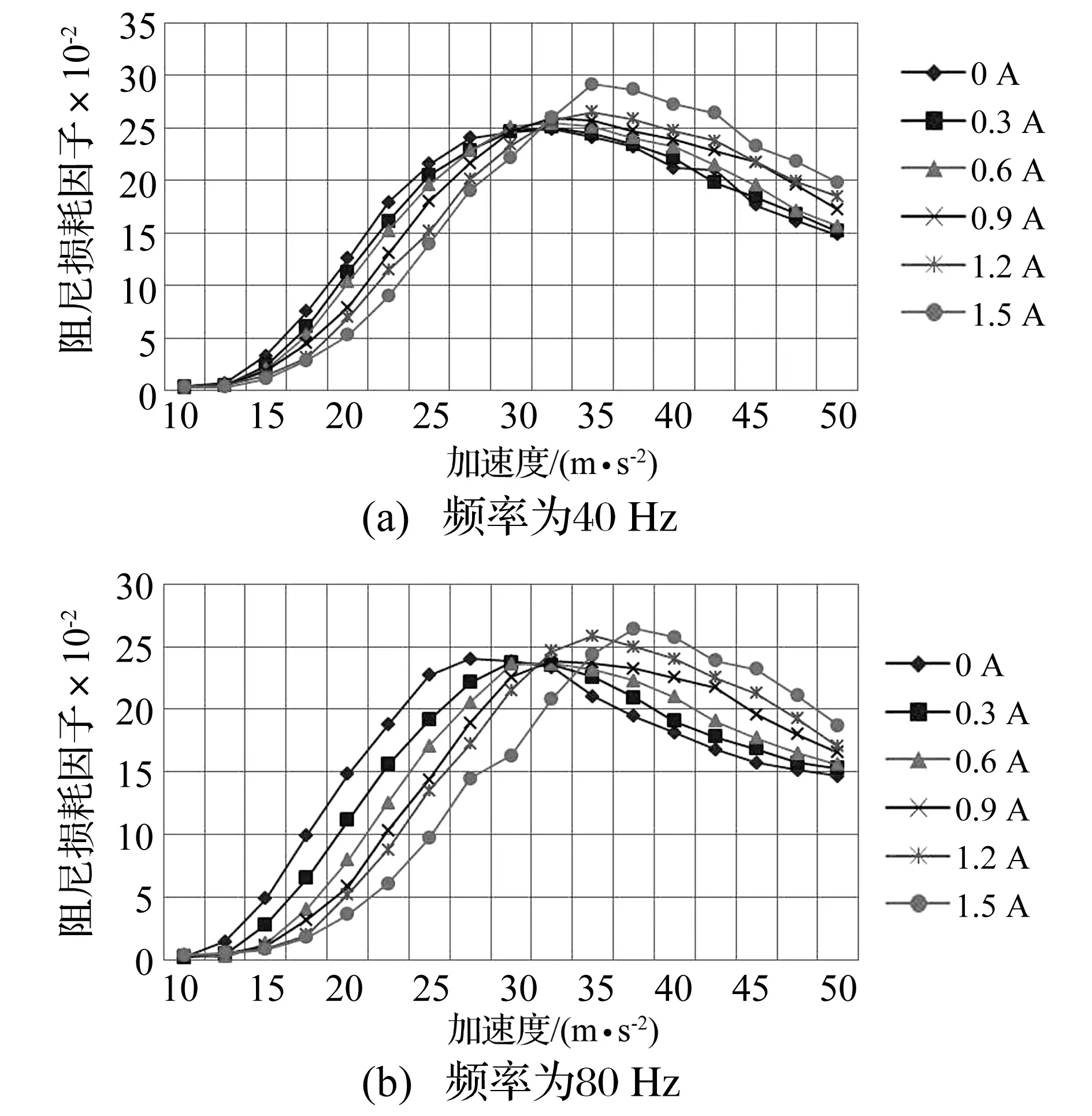
圖5 損耗因子隨加速度幅值變化關系圖Fig.5 Change of loss factor with vibration acceleration

頻率/Hz加速度幅值/(m·s-2)阻尼損耗因子0A1．5A改變百分比/%40250．2150．139-35．3400．2120．27326．9

4.2 損耗功率

同樣選取I=0 A和I=1.5 A時，損耗功率隨頻率及加速度幅值變化的三維曲面圖，如圖6所示。

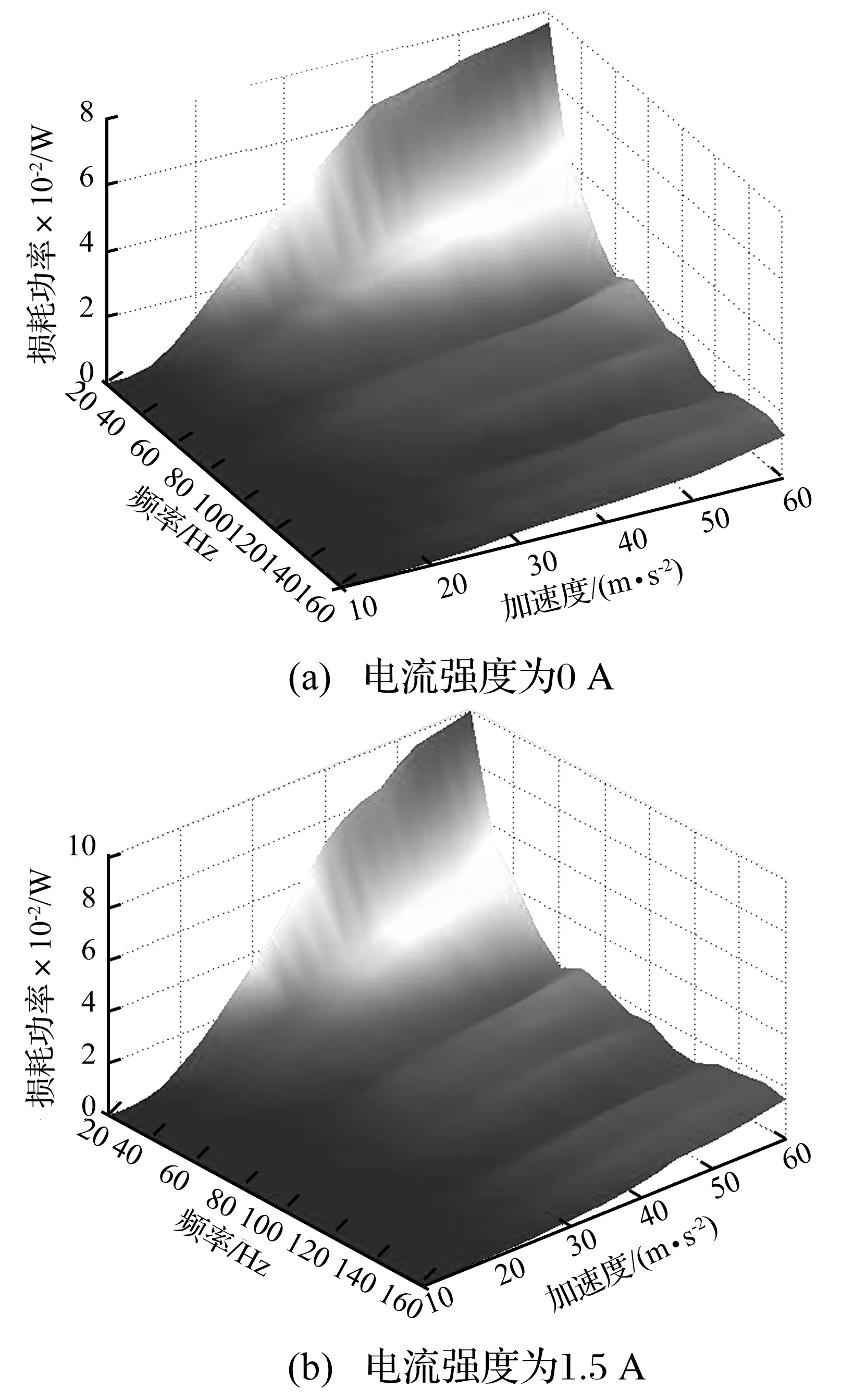
圖6 損耗功率三維曲面圖Fig.6 Loss power three-dimensional surface diagram

選取頻率(f=40 Hz、80 Hz)對損耗功率三維曲面圖進行截取，得到不同電流強度下損耗功率隨加速度變化曲線圖(見圖7)。由圖7可知，當加速度幅值高于某一臨界值時(15 m/s2)，激振力才對阻尼器做功，即只有當系統的激勵加速度達到一定強度時，阻尼顆粒才開始發揮作用，否則阻尼器的損耗功率為零；當加速度大于臨界值后，損耗功率隨激勵強度的增加而單調遞增大。同時可以看出，在較低振動強度下(振動加速度<32.5 m/s2)，損耗功率隨電流強度的增加而減小，即電流產生的磁場減小阻尼顆粒損耗功率；當激勵強度增大到一定值后，損耗功率會隨電流強度的增加而增大，電流產生的磁場會增大阻尼顆粒損耗功率。對比圖5可以看出，損耗因子與損耗功率隨電流強度變化規律相似。

同理，電流為0 A和1.5 A下阻尼器損耗功率對比如表2所示。可以得到，較低振動強度下，施加電流使得損耗功率可減小約30%～40%；當振動強度增大到一定值，施加電流后，損耗功率可增大約20%～30%。

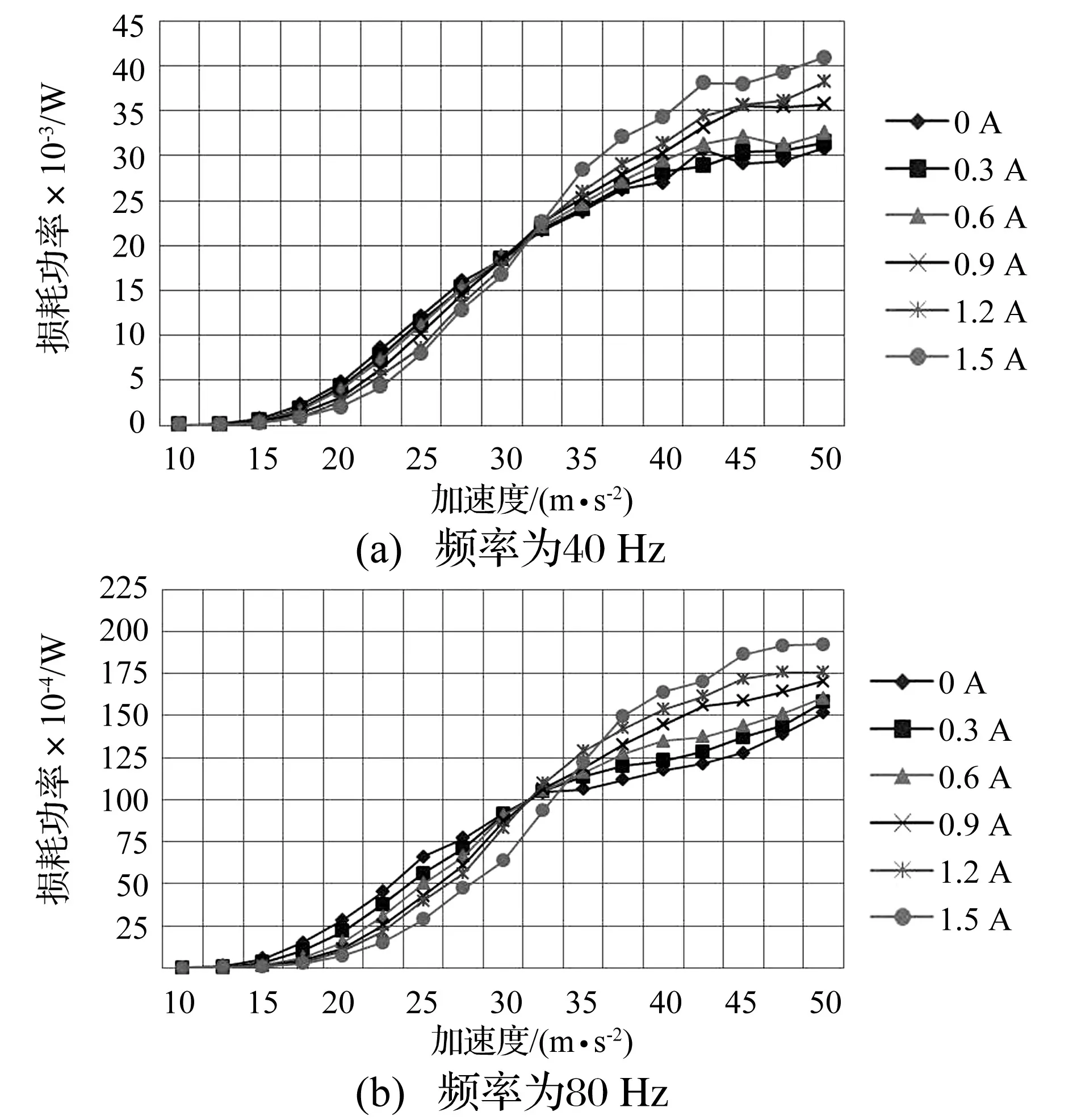
圖7 損耗功率隨加速度幅值變化關系圖Fig.7 Change of loss power with vibration acceleration

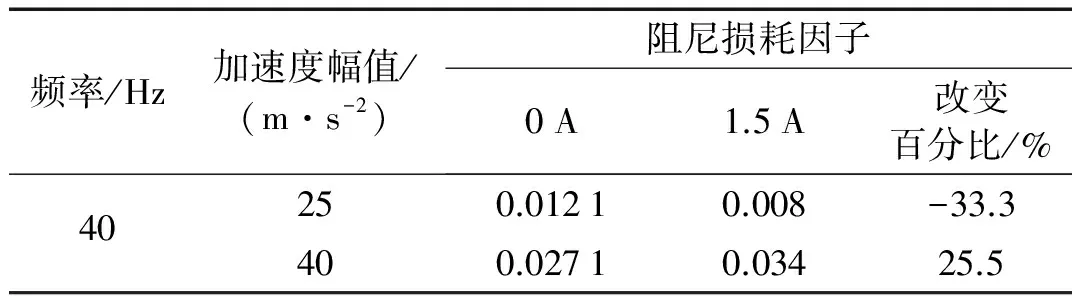
頻率/Hz加速度幅值/(m·s-2)阻尼損耗因子0A1．5A改變百分比/%40250．01210．008-33．3400．02710．03425．5

4.3 有效質量

同理選取I=0 A、I=1.5 A時顆粒阻尼器在不同激勵條件下有效質量(動態質量)的變化情況(見圖8)。由于容器與傳感器之間是固接的，其動態質量不發生變化。因此，曲面實際反映了阻尼顆粒在不同的振動環境下對結構產生附加質量(阻尼器有效質量減去容器質量)的變化趨勢。

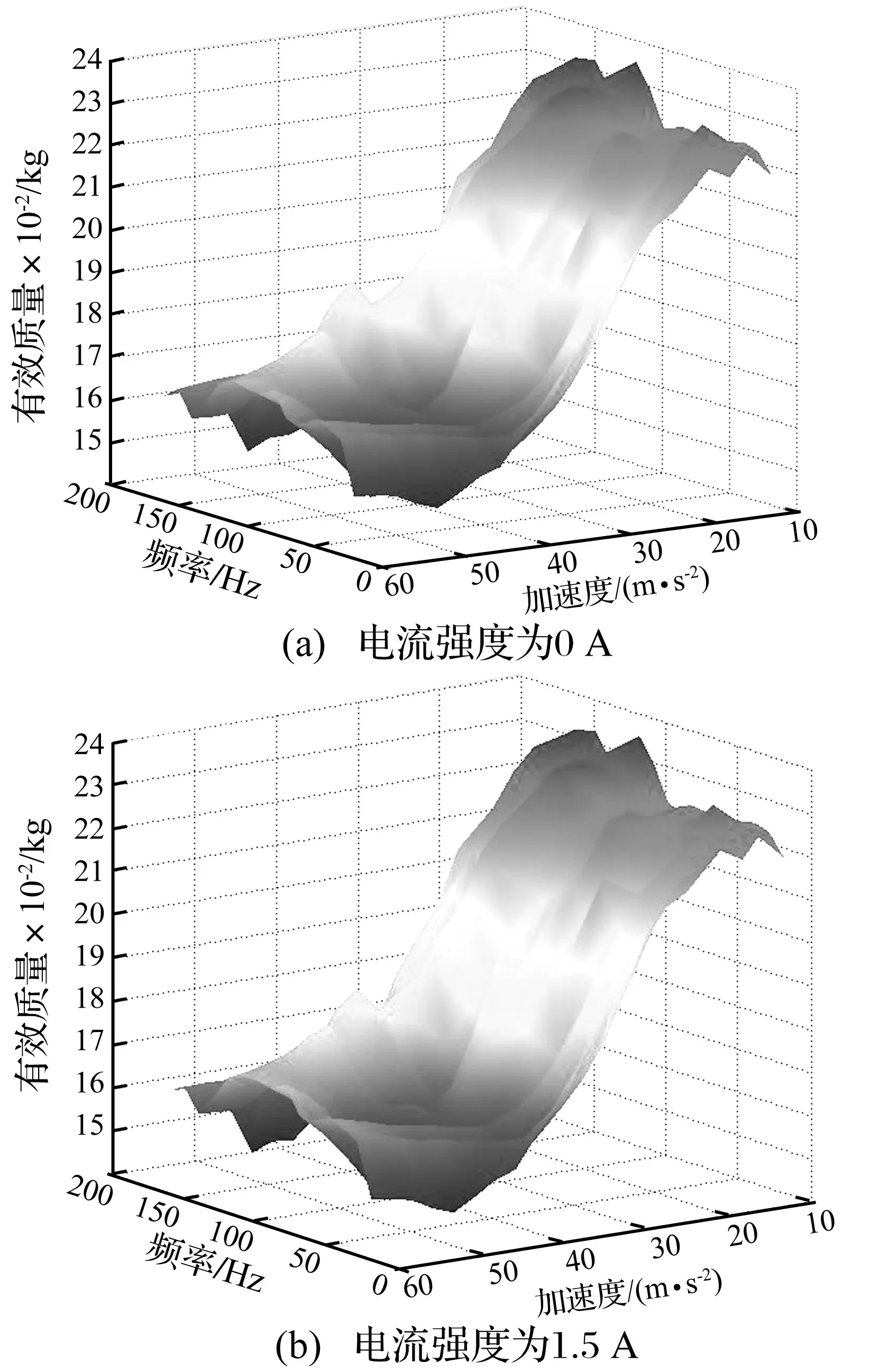
圖8 有效質量三維曲面圖Fig.8 Effective mass three-dimensional surface diagram

選取頻率(f=40 Hz、80 Hz)對有效質量三維曲面圖進行截取，得到阻尼器有效質量在不同電流強度下隨振動加速度變化情況(見圖9)。由圖9可知，阻尼顆粒對結構的附加質量主要受加速度激勵幅值影響，并隨加速度幅值增加呈現先平緩再降低的過程。其中電流為0 A和1.5 A下有效質量對比如表3所示，可以看出電流變化對阻尼顆粒有效質量的改變影響較小。

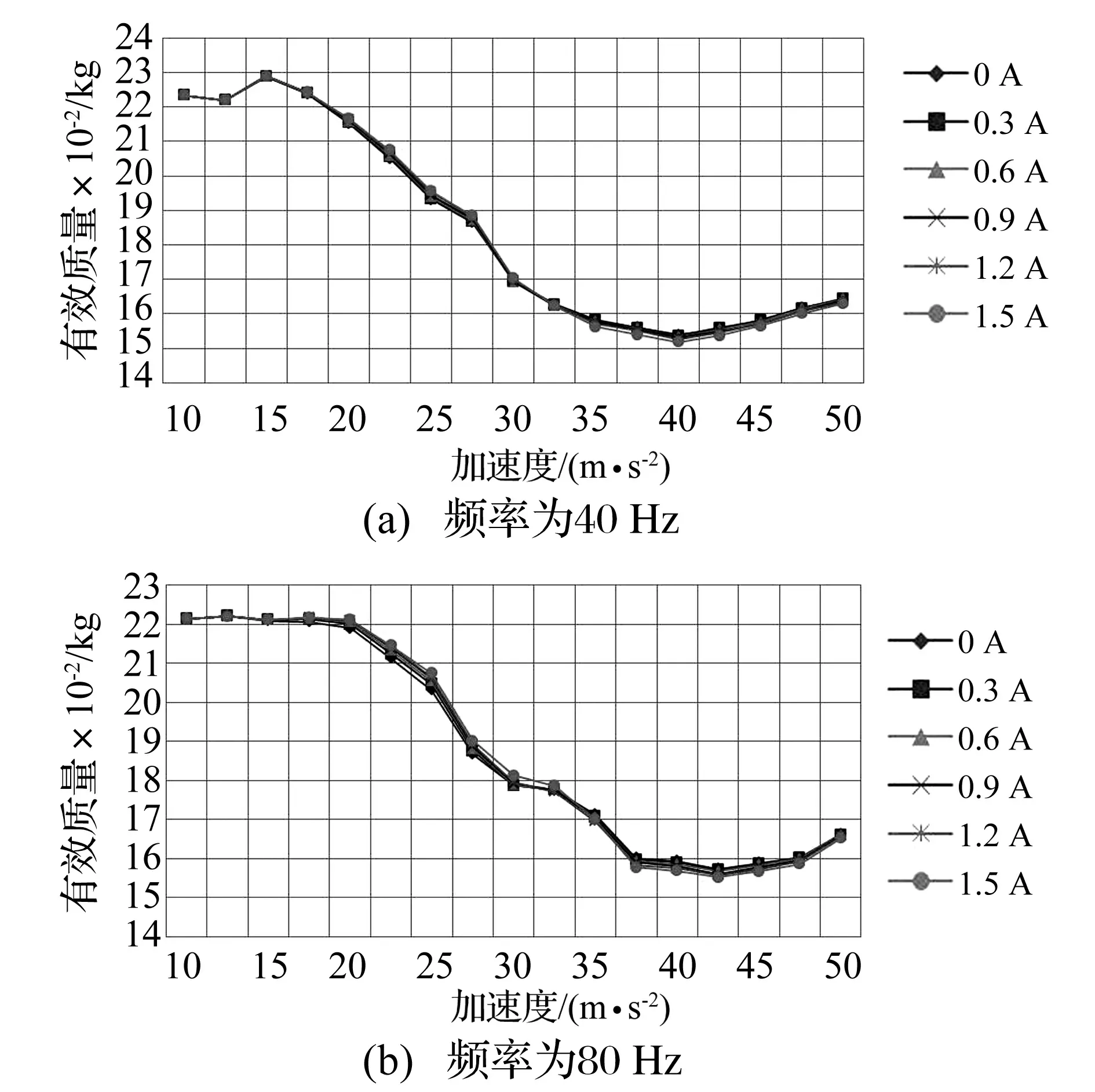
圖9 損耗功率隨加速度幅值變化關系圖Fig.9 Change of effective mass with vibration acceleration

頻率/Hz加速度幅值/(m·s-2)阻尼損耗因子0A1．5A改變百分比/%40250．1930．1961．55400．1540．1521．3

5 結 論

通過文中的試驗研究表明：在一定振動情況下，通過施加直流電磁場的方法，可以改變顆粒阻尼器阻尼性能，從而調節電磁顆粒阻尼器的阻尼特性。在較低振動強度(加速度<32.5 m/s2)下，顆粒體產生的損耗功率和損耗因子隨電流強度的增強而減小，其中數據表明可減小約30%～40%，即顆粒阻尼器阻尼性能隨電磁場強度的增強而減弱；當振動加速度幅值增大到32.5 m/s2后，損耗功率和損耗因子會隨電流強度的增強而增大，可增大約20%～30%，即顆粒阻尼器阻尼性能隨電磁場強度的增大而增強；阻尼顆粒的有效質量隨激勵幅值的增加呈現先平緩再降低的過程，且電流變化對阻尼顆粒的有效質量影響較小。

由于試驗器材性能有限，本文工作中所構建電磁場的強度大小有一定范圍(極限電流為1.5 A)。因此，探究更強電磁場下顆粒阻尼動態特性變化是進一步工作的重點。

[ 1 ] PANOSSIAN H V. An overview of NOPD: a passive damping technique[J]. Shock and Vibration,1991,1(6)：4-10.

[ 2 ] 胡溧，黃其柏，柳占新.顆粒阻尼的動態特性試驗研究[J].振動與沖擊，2009，28(1)：134-137. HU Li，HUANG Qibai，LIU Zhanxin. Dynamic characterstics of particle dampers[J].Journal of Virbration and Shock，2009，28(1):134-137.

[ 3 ] LIU W, TOMLINSON G R, RONGONG J A. The dynamic characterization of disk geometry particle dampers[J].Journal of Sound and Vibration, 2005, 280(3/4/5):849-861.

[ 4 ] SHAH B M, NUDELL J J, KAO K R,et al.Semi-active particle-based damping systems controlled by magnetic fields[J].Journal of Sound and Vibration,2011，330(2):182-193.

[ 5 ] 胡溧，唐喆，徐賢，等.顆粒阻尼器損耗因子外特性研究[J].中國機械工程，2015，26(15)：2005-2009. HU Li，TANG Zhe，XU Xian，et al.Study on external features of particle damping loss factor[J].China Mechanical Engineering,2015，26(15):2005-2009.

[ 6 ] YANG M Y. Development of master design curves for particle impact dampers[D].Pennsylvania: The Pennsylvania State University,2003.

[ 7 ] 李國祥.偶極子在一般外場中的能量與受力[J].安徽大學學報，2001，25(2)：75-77. LI Guoxiang. The force on a dipole and its energy in an external field[J].Journal of Anhui University Natural Science Edition, 2001，25(2)：75-77.

[ 8 ] 何濟洲，繆貴玲. 兩個磁偶極子間的相互作用[J].南昌大學學報，1996，18(3)：96-98. HE Jizhou, MIAO Guiling. The interaction between two magnetic dipoles[J].Journal of Nanchang University, 1996，18(3)：96-98.

[ 9 ] 周宏偉，陳前.電磁顆粒阻尼器減振機理及試驗研究[J].振動工程學報，2008，21(2)：163-166. ZHOU Hongwei, CHEN Qian. Theoretic and experimental investigation on electromagnetic particle damper[J].Journal of Vibration Engineering, 2008，21(2)：163-166.

[10] 毛寬民，陳天寧，黃協清.非阻塞性微顆粒阻尼機理的散體元研究[J].西安交通大學學報，1996，33(9)：80-89. MAO Kuanming, CHEN Tianning, HUANG Xieqing. Mechanism of non-obstructive particle damping with discrete element method[J].Journal of Xi’an Jiaotong University, 1996，33(9)：80-89.

[11] 周宏偉. 顆粒阻尼及其控制的研究與應用[D].南京：南京航空航天大學，2008.

Experimental investigation on dynamic properties of particle damping under electromagnetic field

HULi1，TUDi1，YANGQiliang1，XUXian2

(1.School of Automobile and Traffic Engineering,Wuhan University of Science and Technology, Wuhan 430081, China; 2.Research Center, Dongfeng Commercial Vehicle Co., Ltd., Wuhan 430056, China)

The steady state power technique was used to investigate the damping properties of particle damper which was under the effect of electromagnetic field in experiments. It was observed that the electromagnetic field could change the particle damper’s capability of energy dissipation. Under low vibration acceleration (less than 32.5 m/s2), the loss power and the loss factor decrease with current intensity increases. When the acceleration reaches a higher level, the loss power and the loss factor increase as current intensity increases. When the acceleration amplitude increases, effective mass decreases and current intensity hardly has influence on effective mass.

electromagnetic particle damper; loss power; loss factor; effective mass

國家自然科學基金資助項目(51105283)

2015-10-30 修改稿收到日期：2016-01-14

胡溧 男，博士，副教授，1977年3月生

TB53

A

10.13465/j.cnki.jvs.2017.04.007