基于時間序列的山西省GDP預測分析

韓慧婧++李曉萌

【摘要】GDP即國民生產總值，是衡量一個國家綜合實力的指標。本文在時間序列分析理論的基礎上，以山西省1993年到2013年21年來的GDP總值為基礎，使用 Eviews軟件和Excel對數據進行針對時間的分析，對模型進行檢驗，然后利用本文所建立的模型對山西省未來的6年作出預測。

【關鍵詞】時序分析 GDP ARIMA模型

第一、GDP；即國家國民生產總值，它分析的是一個國家或者地區的生產總值，是衡量經濟發展，經濟規模，經濟水平的重要指標，是反映一個國家的生產力水平。通過分析GDP的發展狀況，我們可以進一步的了解一國的過敏發展情況。

第二、隨著我國的經濟的逐步增長的同時，我們對計量的研究取得了很高的進展，并且在基礎的理論研究方面也有很大的進展，而對于時間序列的理論的分析主要表現有兩個方面，一是單位根的檢驗，二是非線性模型的研究。

第三、實證分析。本文以山西省的國民生產總值數據作為例子，在傳統的模型的基礎上，利用時序的分析方法，借助常用的數據分析的軟件，以時序平均值、標準差等等的參數，同時評價模型準則，建立山西省時間序列模型，分析經濟增長的內在特征。比較山西省的指數模型和時序模型，并對未來6年的國民經濟GDP做出預測，為政府制定對應的宏觀經濟發展戰略，同時也為政府作出最終決策提供數據依據。

我省GDP在總體上來觀察，是表現出很明顯的上升趨勢的，可以發現原來序列是非平穩的。可以進一步進行ADF檢驗，檢驗t統計量的值為0.426184，顯著性水平1%，5%，10%的臨界值分別-3.920350，-3.065585，-2.673459，可見t統計量的值大于各顯著性水平的臨界值，且p值明顯大于0.05，故接受原假設，認為序列不平穩。為了可以更好的進行數據分析，通常必須要求數據序列是平穩的，所以我們有兩種方法可以使數據平穩化：一是取對數，二是差分法。

對數據進行對對數化處理，再進行二階查分后，判斷進行ADF檢驗，檢驗t統計量的值為-4.746491，由得出的結果可以觀察到，所以t統計量的值小于其不同水平的臨界值，而且p值遠小于0.05，所以這里，可以認為是拒絕原假設，認為我們的序列是平穩的。這里，數據序列經過二階差分后是平穩的，所以相應模型的差分階數就可以定為2。

我們可以通過觀察模型的自相關和偏自相關系數來定階，通關觀察發現，滯后三階就呈現出了拖尾現象，所以我們可以選用ARIMA（1，2，1）和ARIMA（1，2，2）模型進行參數估計。

通過分析上面四圖中數據以及相應的參數估計結果，我們可以得到，ARIMA（1，2，1） 和ARIMA（1，2，2）模型的滯后多項式倒數根均落在單位圓內，滿足過程的平穩要求。但是，由于調整后的ARIMA（1，2，2）的Adjusted R^2值比ARIMA（1，2，1）的調整后的R方值大，且兩個模型的AIC值和SC值相差小，故選擇ARIMA（1，2，2）模型更好。做完模型的構建和參數估計的工作之后，需要檢查和分析對應統計數據結果，來判斷所選的模型能否符合要求。在所有值都大于0.05，接受殘差為我們隨機序列的假設。再進行對應異方差的White檢驗。所以表明該序列為白噪聲序列，所以信息的提取很充分，模型也選擇的比較合理。綜合比較上述兩個模型，ARIMA（1，2，1）更合理。所以我們用ARIMA（1，2，1）模型對山西省GDP進行分析預測。

由山西省統計年鑒報告可知，山西省2014年GDP的實際值為1275944（百萬元）。將2014年山西省GDP的預測值與實際值進行比較，來判定模型的合理性。

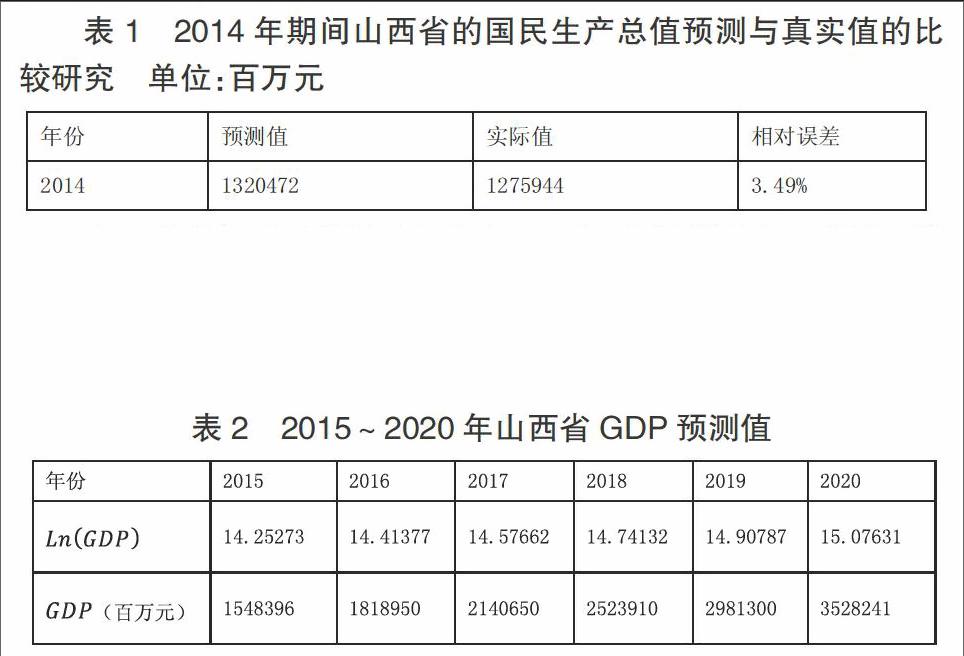
表1 2014年期間山西省的國民生產總值預測與真實值的比較研究 單位：百萬元

■

由上表我們可以得到，MAE和MAPE的值都很小，表明了預測模型較好，通過驗證了山西省2014年的數據，發現預測結果的相對誤差可以小于5%，說明預測效果很好。所以，我們選擇ARIMA（1，2，1）模型對山西省未來6年的GDP作出預測，如下表所示：

表2 2015～2020年山西省GDP預測值

■

第四，結論。通過對山西省1993～2013年的GDP進行時序分析，我們建立了ARIMA（1，2，1）模型，通過對模型進行檢測，我們判定該模型符合數據所需的要求，可以滿足預測條件，通過對2014年山西省的GDP進行預測，并且比較了預測值與實際值的相對誤差，結果為相對誤差很小，我們繼續對山西省的2015年至2020年的6年內的山西省GDP進行了預測，其呈現增長趨勢，說明其符合經濟發展的一般規律，為山西省的經濟政策提供了可參考的價值。

參考文獻

[1]門小琳.組合預測方法在我國CPI預測中的應用.南京財經大學碩士論文[D].2012年.

[2]趙紫旭.現階段推進我國基本公共服務均等化對策研究.渤海大學碩士論文[D].2012年.

[3]陳敏.1993.時間序列分析.北京：高等教育出版社：113-196.

[4]戴思銳.2003.計量經濟學.北京：中國農業出版社：298-299.

作者簡介：韓慧婧（1991-），女，山西大同人，山西財經大學2015（統計學）學術碩士究生，研究方向：金融高頻數據；李曉萌（1993-），女，山西運城人，山西財經大學2015（統計學）學術碩士研究生，研究方向：多維貧困測度方法及不平等研究。