組合梁考慮滑移效應(yīng)的理論分析

肖巖+彭羅文

摘 要：鋼混凝土組合梁的剛度和撓度分析因可能受到兩者界面的相對(duì)滑移影響而十分復(fù)雜.針對(duì)組合梁受界面滑移效應(yīng)的影響，進(jìn)行了靜力線(xiàn)彈性分析，提出了組合梁撓度計(jì)算的二階算法，分別建立了關(guān)于組合梁考慮滑移效應(yīng)的撓度和層間相對(duì)滑移的二階常微分方程，給出了相應(yīng)的邊界條件，求得了簡(jiǎn)支梁、懸臂梁、兩端固定梁和一端簡(jiǎn)支一端固定梁4種不同邊界條件組合梁在不同荷載作用下的層間相對(duì)滑移和撓度的理論精確解，并給出了組合梁受層間滑移效應(yīng)影響的內(nèi)力計(jì)算.通過(guò)與組合梁撓度計(jì)算高階算法的對(duì)比，二階算法簡(jiǎn)化了組合梁考慮滑移效應(yīng)的撓度計(jì)算，給出了相對(duì)全面的計(jì)算結(jié)果.

關(guān)鍵詞：組合梁；滑移效應(yīng)；撓度

中圖分類(lèi)號(hào)：TU398.9 文獻(xiàn)標(biāo)志碼：A

組合梁具有剛度大、承載能力高等優(yōu)點(diǎn)，在建筑結(jié)構(gòu)、橋梁結(jié)構(gòu)等領(lǐng)域得到了廣泛應(yīng)用[1].然而，廣泛應(yīng)用于實(shí)際工程的栓釘?shù)热嵝钥辜暨B接件由于受到鋼梁與混凝土翼緣板之間水平剪力的作用而產(chǎn)生變形，引起交界面產(chǎn)生滑移，從而使組合梁剛度降低，撓度也相應(yīng)增大.因此，相對(duì)精確的計(jì)算正常使用極限狀態(tài)下組合梁考慮滑移效應(yīng)的撓度十分重要.

國(guó)內(nèi)外眾多專(zhuān)家學(xué)者對(duì)組合梁的滑移效應(yīng)和撓度計(jì)算等進(jìn)行了深入研究[2]，在大量實(shí)驗(yàn)研究和理論分析的基礎(chǔ)上提出了各種不同的滑移、內(nèi)力和撓度等計(jì)算方法.Newmark等[3]進(jìn)行了組合梁考慮滑移效應(yīng)線(xiàn)彈性分析的早期研究.Girhammar 和Gopu[4]對(duì)組合梁進(jìn)行了內(nèi)力分析，建立了關(guān)于組合梁考慮滑移效應(yīng)撓度的六階常微分方程.聶建國(guó)等[5]在理論分析的基礎(chǔ)上建立了簡(jiǎn)支梁界面滑移微分方程，給出了簡(jiǎn)支梁變形計(jì)算的一般公式，并提出了組合梁變形計(jì)算的折減剛度法[6].盡管在其推導(dǎo)過(guò)程中附加曲率取層間相對(duì)滑移應(yīng)變與組合梁高度之比Δφ=εs/h值得商榷，另外取e-αL≈0也會(huì)造成一定程度的誤差，但是，折減剛度法使得組合梁的設(shè)計(jì)變得簡(jiǎn)潔，從而促進(jìn)了其推廣應(yīng)用.朱聘儒[7]對(duì)簡(jiǎn)支梁在均布荷載作用下的撓度計(jì)算進(jìn)行了分析計(jì)算.童根樹(shù)等[8]建立了簡(jiǎn)支梁均布荷載作用下的高階微分方程，得到了簡(jiǎn)支梁的撓度計(jì)算公式.Girhammar 和Pan[9]通過(guò)虛功原理建立了組合梁撓度計(jì)算的微分方程，得到了組合梁撓度計(jì)算的一般表達(dá)式.在此基礎(chǔ)上，Girhammar[10]提出了組合梁考慮滑移效應(yīng)靜力計(jì)算的簡(jiǎn)化方法.蔣麗忠等[11]在Goodman彈性?shī)A層假設(shè)和彈性體變形理論的基礎(chǔ)上，對(duì)簡(jiǎn)支組合梁在均布荷載作用下的界面滑移和撓度計(jì)算進(jìn)行了分析研究， 推導(dǎo)出了簡(jiǎn)支組合梁的界面滑移和撓度的計(jì)算公式.余志武等[12]給出了簡(jiǎn)支組合梁在集中荷載作用下的界面滑移和撓度的理論計(jì)算公式.苗林和陳德偉[13]利用Goodman 彈性?shī)A層法分析了雙層組合梁在彈性工作階段的滑移、內(nèi)力及撓度與荷載之間的關(guān)系.胡夏閩等[14]采用曲率等效原則提出了組合梁撓度計(jì)算的附加曲率法.

組合梁考慮滑移效應(yīng)的各個(gè)計(jì)算方法都有各自的特點(diǎn)和適用范圍，其中部分計(jì)算方法只對(duì)簡(jiǎn)支梁進(jìn)行了分析計(jì)算，并未考慮其他邊界條件的組合梁，尤其是對(duì)超靜定梁精確解的計(jì)算.同時(shí)我國(guó)《鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范》（GB50017—2003）[15]中，會(huì)出現(xiàn)隨剪力連接程度的增大組合梁考慮滑移效應(yīng)的折減剛度B反而減小，撓度反而增大的反常情況，這些問(wèn)題都值得進(jìn)一步的分析研究與對(duì)比.本文選取組合梁中任一微元體為研究對(duì)象進(jìn)行詳細(xì)的靜力線(xiàn)彈性分析，建立組合梁考慮滑移效應(yīng)的二階算法來(lái)簡(jiǎn)化組合梁的撓度計(jì)算，分別建立撓度和層間相對(duì)滑移的二階常微分方程，并與組合梁考慮滑移效應(yīng)撓度計(jì)算的高階算法進(jìn)行對(duì)比.利用二階算法通過(guò)相應(yīng)的邊界條件，求得4種不同邊界條件組合梁的撓度，同時(shí)給出組合梁受到層間滑移影響的內(nèi)力計(jì)算.

1 組合梁微分方程的建立

組合梁考慮滑移效應(yīng)理論分析的基本假設(shè)：

1） 組合梁各個(gè)子構(gòu)件材料均為線(xiàn)彈性，撓度均為小變形；

2） 組合梁剪力連接件均勻布置，交界面上的層間滑移力與層間相對(duì)滑移成正比；

3） 組合梁各個(gè)子構(gòu)件之間不會(huì)發(fā)生豎向剝離，各個(gè)子構(gòu)件的曲率和撓度均相等；

4） 組合梁各個(gè)子構(gòu)件均不考慮剪切變形，并分別符合平截面假定.

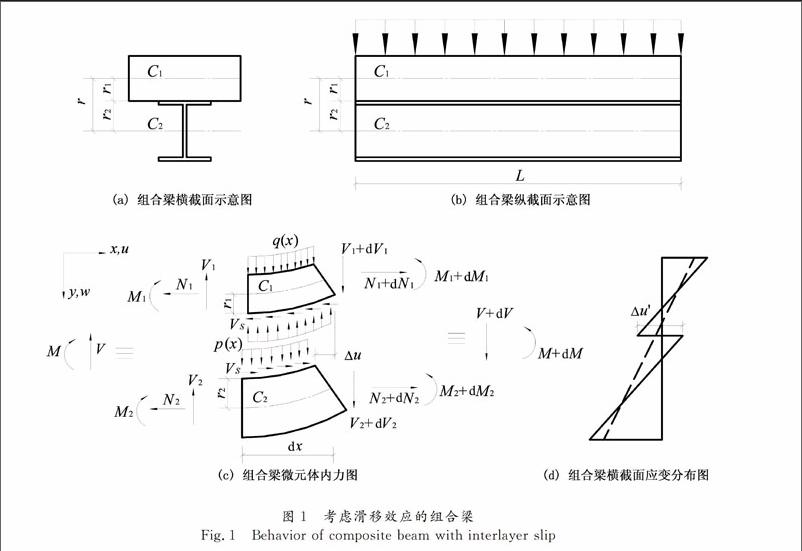
組合梁由子構(gòu)件1和子構(gòu)件2通過(guò)剪力連接件連接而成，取組合梁一微元體進(jìn)行受力分析，如圖1所示.在任意荷載q（x）作用下，組合梁橫截面如圖1（a）所示，組合梁縱截面如圖1（b）所示，組合梁微元體內(nèi)力如圖1（c）所示，組合梁橫截面應(yīng)變分布如圖1（d）所示，其中不考慮滑移效應(yīng)的應(yīng)變分布用虛線(xiàn)表示，考慮滑移效應(yīng)的應(yīng)變分布用實(shí)線(xiàn)表示.組合梁及其子構(gòu)件1和2所受軸力、剪力、彎矩、層間滑移力以及層間掀起力分別表示為N，V，M，VS和p（x），其中下標(biāo)1和2分別表示子構(gòu)件1和2.組合梁沿坐標(biāo)軸x和y方向的位移分別表示為u和w.子構(gòu)件1和2的中性軸位置分別表示為C1和C2.子構(gòu)件1和2中性軸到其交界面的距離分別表示為r1和r2，子構(gòu)件1和2中性軸之間的距離表示為r，其中r= r1+ r2.子構(gòu)件1和2之間的層間相對(duì)滑移表示為Δu.各個(gè)物理量的正方向均如圖1所示.

式中：Acf為混凝土翼緣板的橫截面面積；Icf為混凝土翼緣板的橫截面慣性矩；A為鋼梁的橫截面面積；I為鋼梁的橫截面慣性矩；dc為鋼梁橫截面與混凝土翼緣板橫截面的形心距；h為組合梁高度；l為組合梁跨度；p為抗剪連接件平均縱向間距；k為連接件的剛度系數(shù)；ns為連接件的列數(shù)；αE為鋼材相對(duì)于混凝土材料的彈性模量之比.

由公式（66）～（73），折減剛度B采用本文統(tǒng)一符號(hào)可表示為：

B=EI

SymboleB@ 1+18αL2·EI0EI

SymboleB@ 0.4-30.81αL2（74）

規(guī)范的撓度放大系數(shù)Φ采用本文統(tǒng)一符號(hào)可表示為：

Φ=1+18αL2·EI0EI

SymboleB@ 0.4-30.81αL2（75）

由公式（74）可知，折減剛度B隨著組合效應(yīng)系數(shù)αL變化呈現(xiàn)拋物線(xiàn)變化.當(dāng)αL≤3.38時(shí)，折減剛度B為負(fù)值，顯然錯(cuò)誤，雖然規(guī)范中規(guī)定當(dāng)ζ≤0時(shí)，取ζ=0，但缺乏相關(guān)理論依據(jù)；當(dāng)3.38≤αL≤4.78時(shí)，折減剛度B隨剪力連接程度（即組合效應(yīng)系數(shù)αL）的增大反而減小，可見(jiàn)規(guī)范存在不合理之處.

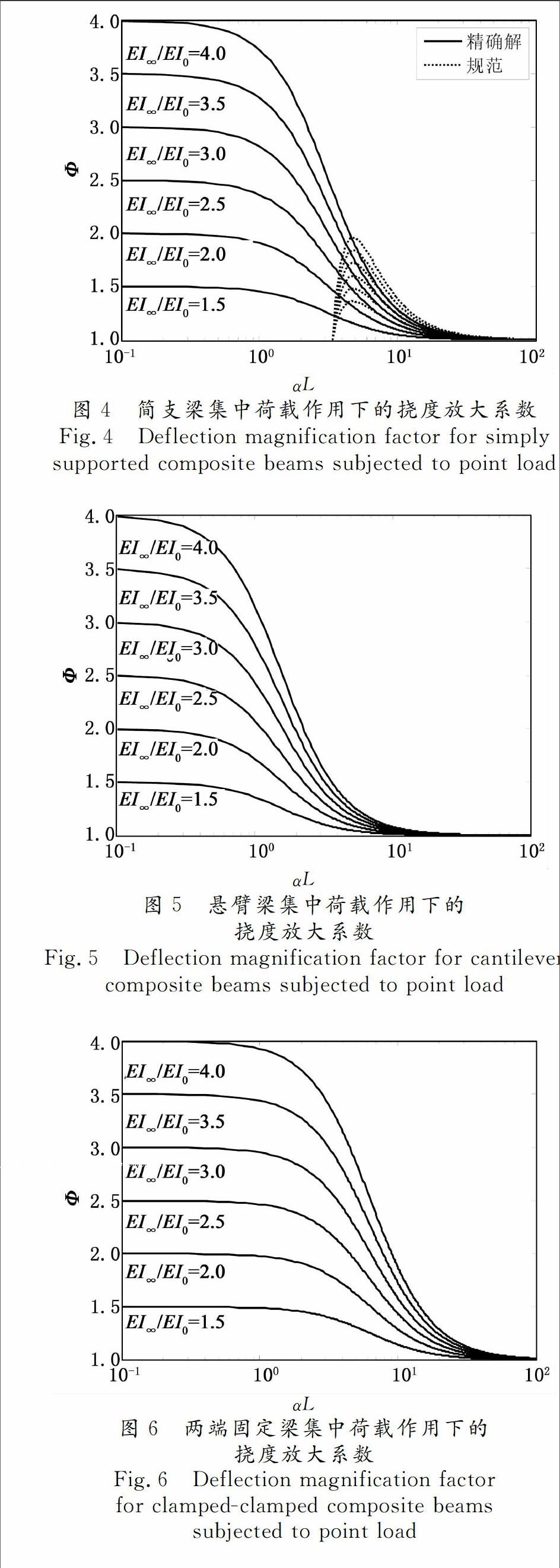
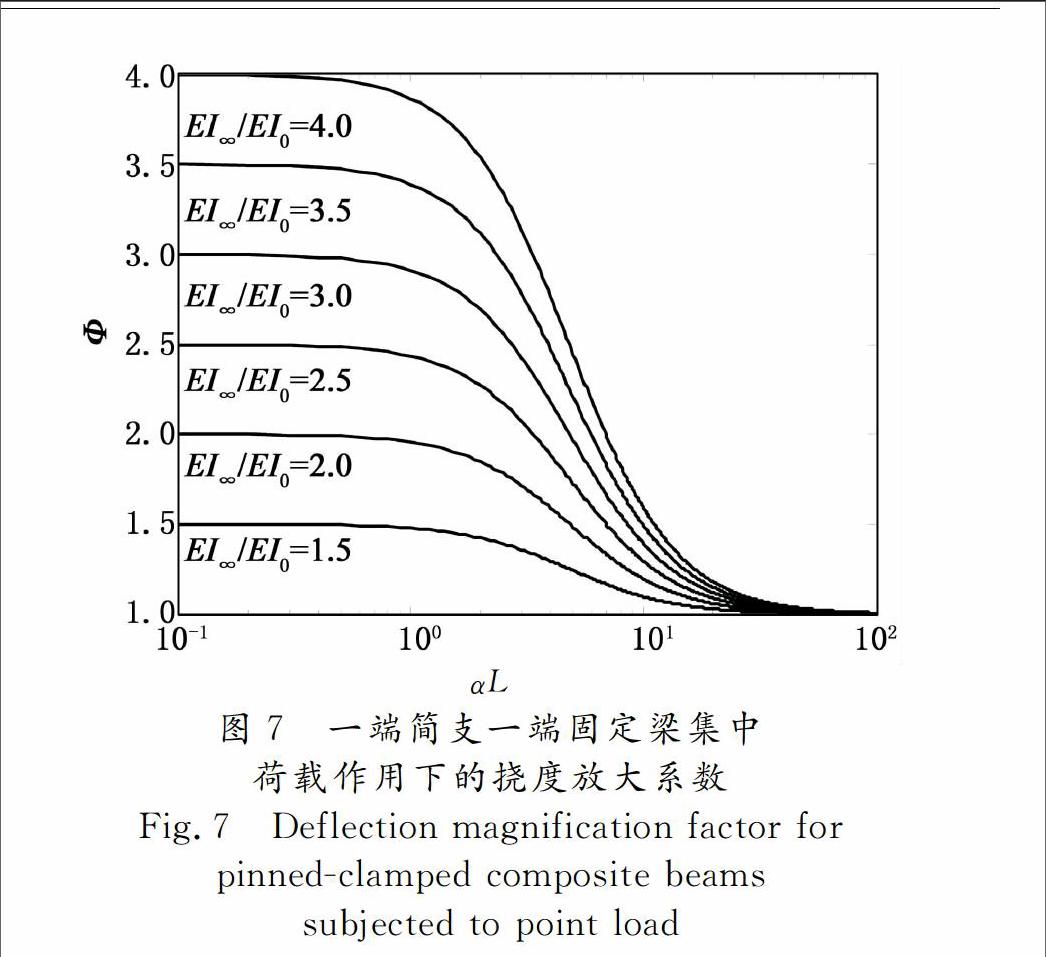
由公式（66）和表1可得，集中荷載作用下，4種不同邊界條件組合梁的撓度放大系數(shù)Φ如圖4～圖7所示，組合梁完全剪力連接與完全無(wú)剪力連接的剛度比EI

SymboleB@ /EI0如圖4～圖7所示.

由圖4～圖7可知，對(duì)于4種不同邊界條件的組合梁，當(dāng)組合效應(yīng)系數(shù)αL趨于0時(shí)，撓度放大系數(shù)Φ趨于剛度比EI

SymboleB@ /EI0，組合梁趨于完全無(wú)剪力連接；當(dāng)組合效應(yīng)系數(shù)αL不斷增大，即剪力連接程度不斷增大時(shí)，撓度放大系數(shù)Φ趨于1，組合梁趨于完全剪力連接.滿(mǎn)足組合梁的兩種極限狀態(tài)現(xiàn)象：完全無(wú)剪力連接與完全剪力連接.

規(guī)范中折減剛度是在簡(jiǎn)支梁的求解基礎(chǔ)上得到的，并沒(méi)有針對(duì)其他邊界條件的組合梁進(jìn)行相關(guān)說(shuō)明，因此不能應(yīng)用于其它邊界條件的組合梁.圖4中，采用規(guī)范的撓度放大系數(shù)與精確解相差較大，可見(jiàn)我國(guó)規(guī)范相關(guān)內(nèi)容有待進(jìn)一步補(bǔ)充與改進(jìn).

6 結(jié) 論

本文針對(duì)組合梁受界面滑移效應(yīng)的影響，進(jìn)行了靜力線(xiàn)彈性分析，建立了組合梁考慮滑移效應(yīng)的微分方程，得到了以下結(jié)論：

1） 建立了組合梁撓度計(jì)算的二階算法.建立了分別關(guān)于組合梁考慮滑移效應(yīng)撓度w和層間相對(duì)滑移Δu的二階常微分方程，并且給出了相應(yīng)的邊界條件.

2） 組合梁撓度計(jì)算的二階算法可將組合梁考慮滑移效應(yīng)撓度w中由于滑移效應(yīng)產(chǎn)生的附加撓度Δw單獨(dú)分離出來(lái)進(jìn)行計(jì)算.同時(shí)，在計(jì)算過(guò)程中計(jì)算求得出了組合梁的層間相對(duì)滑移Δu，對(duì)于研究組合梁的滑移效應(yīng)提供了一個(gè)重要的參數(shù).

3） 本文提出的二階算法簡(jiǎn)化了組合梁考慮滑移效應(yīng)的撓度計(jì)算，與以往文獻(xiàn)中的高階算法相比具有更好的優(yōu)越性，建議采用組合梁撓度計(jì)算的二階算法進(jìn)行相關(guān)分析計(jì)算.

4） 建立了組合梁考慮滑移效應(yīng)的內(nèi)力計(jì)算公式.

5） 給出了相對(duì)嚴(yán)密和全面的撓度計(jì)算結(jié)果，求得了4種不同邊界條件組合梁撓度和層間相對(duì)滑移的理論精確解.

參考文獻(xiàn)

[1] 毛小勇， 肖巖. 標(biāo)準(zhǔn)升溫下輕鋼-混凝土組合梁的抗火性能研究[J]. 湖南大學(xué)學(xué)報(bào)： 自然科學(xué)版， 2005， 32（2）： 64-70.

MAO Xiaoyong， XIAO Yan. Behavior of lightweight steelconcrete composite beams subjected to standard fire [J]. Journal of Hunan University： Natural Sciences， 2005， 32（2）： 64-70. （In Chinese）

[2] 邵旭東， 劉俊珂. 計(jì)入加勁肋的圓孔蜂窩組合梁強(qiáng)度簡(jiǎn)化計(jì)算[J]. 湖南大學(xué)學(xué)報(bào)： 自然科學(xué)版， 2009， 36（9）： 7-11.

SHAO Xudong， LIU Junke. Reduced computation of the strength of circular hole castellated composite beams with stiffened webs [J]. Journal of Hunan University： Natural Sciences， 2009， 36（9）： 7-11. （In Chinese）

[3] NEWMARK N M， SIESS C P， VIEST I M. Tests and analysis of composite beams with incomplete interaction [J]. Society for Experimental Stress Analysis， 1951， 9（1）： 75-92.

[4] GIRHAMMAR U A， GOPU V K. Composite beamcolumns with interlayer slipexact analysis [J]. Journal of Structural Engineering， 1993， 119（4）： 1265-1282.

[5] 聶建國(guó)， 沈聚敏， 袁彥聲. 鋼混凝土簡(jiǎn)支組合梁變形計(jì)算的一般公式[J]. 工程力學(xué)， 1994， 11（1）： 21-27.

NIE Jianguo， SHEN Jumin， YUAN Yansheng. A general formula for calculating the deformation of simply supported steelconcrete composite beams [J]. Engineering Mechanics， 1994， 11（1）： 21-27. （In Chinese）

[6] 聶建國(guó)， 沈聚敏， 余志武. 考慮滑移效應(yīng)的鋼-混凝土組合梁變形計(jì)算的折減剛度法[J]. 土木工程學(xué)報(bào)， 1995， 28（6）： 11-17.

NIE Jianguo， SHEN Jumin， YU Zhiwu. A reduced stiffness method for calculating deformation of steelconcrete composite beams with the consideration of slip effect [J]. China Civil Engineering Journal， 1995， 28 （6）： 11-17. （In Chinese）

[7] 朱聘儒. 鋼-混凝土組合梁設(shè)計(jì)原理[M]. 北京：中國(guó)建筑工業(yè)出版社， 2006： 76-96.

ZHU Pinru. Principles of steelconcrete composite beams design [M]. Beijing： China Architecture & Building Press， 2006： 76-96. （In Chinese）

[8] 童根樹(shù)， 夏駿. 考慮滑移影響的鋼-混凝土組合梁的剛度[J]. 建筑鋼結(jié)構(gòu)進(jìn)展， 2008， 10（6）： 1-8.

TONG Genshu， XIA Jun. Bending stiffness of steelconcrete composite beams considering effect of slip [J]. Progress in Steel Building Structures， 2008， 10（6）：1-8. （In Chinese）

[9] GIRHAMMAR U A， PAN D H. Exact static analysis of partially interaction composite beams and beamcolumns [J]. International Journal of Mechanical Sciences， 2007， 49（2）： 239-255.

[10]GIRHAMMAR U A. A simplified analysis method for composite beams with interlayer slip [J]. International Journal of Mechanical Sciences， 2009， 51（7）： 515-530.

[11]蔣麗忠， 余志武， 李佳. 均布荷載作用下鋼混凝土組合梁滑移及變形的理論計(jì)算[J]. 工程力學(xué)， 2003， 20（2）： 133-137.

JIANG Lizhong， YU Zhiwu， LI Jia. Theoretical analysis of interlayer slip and deformation of steelconcrete composite beams under uniformly distributed loads [J].Engineering Mechanics， 2003， 20（2）： 133-137. （In Chinese）

[12]余志武， 蔣麗忠， 李佳. 集中荷載作用下鋼混凝土組合梁界面滑移及變形[J]. 土木工程學(xué)報(bào)， 2003， 36（8）： 1-6.

YU Zhiwu， JIANG Lizhong， LI Jia. Interlayer slip and deformation of steelconcrete composite beams under concentrated loads [J]. China Civil Engineering Journal， 2003， 36（8）： 1-6. （In Chinese）

[13]苗林， 陳德偉. 考慮層間滑移效應(yīng)的組合梁解析計(jì)算[J]. 同濟(jì)大學(xué)學(xué)報(bào)： 自然科學(xué)版， 2011， 39（8）： 1113-1119.

MIAO Lin， CHEN Dewei. Closedform solution of composite beam considering interfacial slip effects [J]. Journal of Tongji University： Natural Science， 2011， 39（8）： 1113-1119. （In Chinese）

[14]胡夏閩， 薛偉， 曹雪嬌. 鋼-混凝土組合梁撓度計(jì)算的附加曲率法[J]. 建筑結(jié)構(gòu)學(xué)報(bào)， 2010（增刊1）： 385-389.

HU Xiamin， XUE Wei， CAO Xuejiao. The additional curvature method for calculating deflection of steelconcrete composite beams [J]. Journal of Building Structures， 2010（S1）：385-389. （In Chinese）

[15]GB 50017-2003 鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范[S]. 北京： 中國(guó)計(jì)劃出版社， 2003： 108-119.

GB 50017-2003 Code for design of steel structures [S].Beijing： China Planning Press， 2003： 108-119. （In Chinese）