風機葉片多點激振疲勞加載試驗分析

烏建中，馬 怡

（同濟大學機械與能源工程學院，上海201804）

風機葉片疲勞加載試驗的目的是測試葉片的可靠性和抗疲勞強度，確保葉片疲勞壽命達到設計要求。隨著風機技術的發展，大批兆瓦級大型風機投入規模化的生產，單點加載可能難以驅動大尺寸葉片試驗，而使用多套設備在不同點同時進行加載，即多點疲勞加載，可以加大激振能力，同時能更好地滿足彎矩分布要求，提高測試頻率，縮短試驗時間[1-2]。本文建立了多點葉片疲勞加載振動模型，并以兩點為例設計了多點疲勞加載系統。

1 風機葉片兩點疲勞加載試驗系統組成

風機葉片疲勞加載試驗系統由加載基座、測試葉片、疲勞加載系統等構成，其中疲勞加載系統由動力裝置、可移動質量塊和固定部分等構成。風機葉片的根部固定在加載基座上，多點激振試驗是多個加載源布置在沿葉片展向位置上，其動力裝置驅動可移動質量塊做直線往復運動，其產生的慣性力對葉片進行加載，以兩點激振疲勞加載試驗系統為例，如圖1所示。

2 風機葉片疲勞加載振動模型建立

2.1 葉片模型離散化

將連續的葉片分為各截面，離散成一個具有自由度的等效懸臂桿體系，每個離散段為一個單元，由無質量的梁段及截面處的集中質量塊組成，如圖2所示。

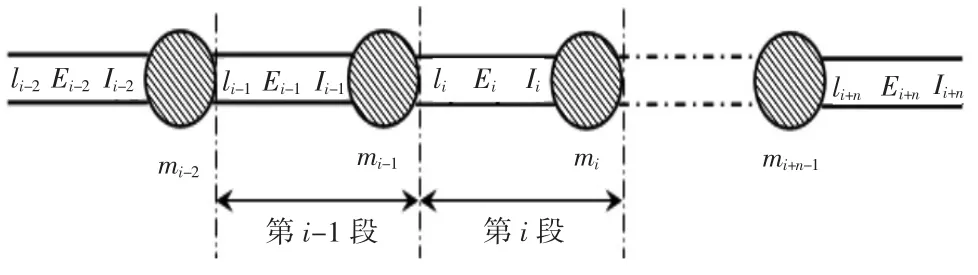
圖2 葉片離散化模型

葉片根部記為截面1，尖部為截面n，截面i與截面i+1組成離散段i.離散段長度為li，截面線密度為ρi，則離散段i的質量近似為：

n自由度系統的運動微分方程為：

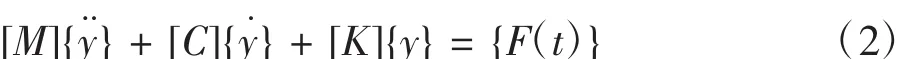
上式中：[M]為結構的質量矩陣，是對角線元素為集中質量mi的對角線矩陣；[K]為結構的抗彎剛度矩陣；[C]為結構的阻尼矩陣；{y}、{y˙}、{y¨}分別為結構的位移、速度和加速度；{F（t）}為激振力向量。

2.2 葉片系統受迫振動分析

多自由度系統的固有振動分析可歸結為求解矩陣特征值問題，當自由度數較大時計算量非常大，本文采用傳遞矩陣法進行振動分析。離散化的等效懸臂桿體系中一個典型單元包括一個無質量梁段和一個集中質量 mi，分別如圖 3（a）和（b）所示，用 4 個矢量來表示每個單元截面的狀態量Z：撓度yi、轉角θi、剪力Qi和彎矩Mi.

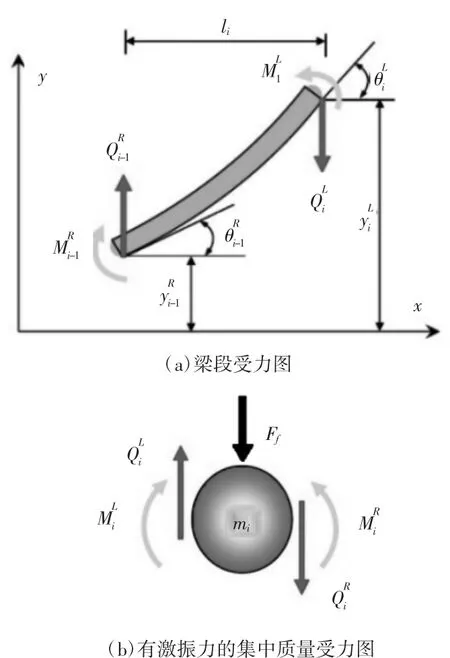
圖3 梁段受和有激振力的集中質量受力圖

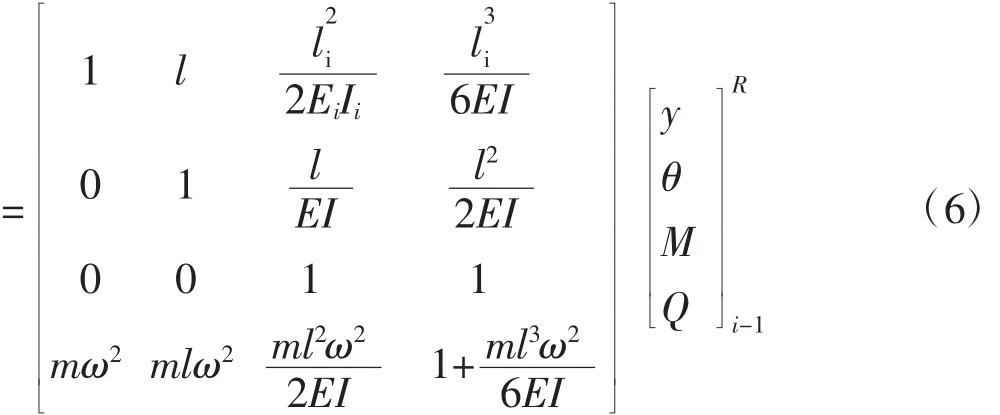
傳遞關系式按順序相乘，可得一個4×4矩陣，用u11與u44表示矩陣元素，得振動系統的狀態矢量傳遞關系為：

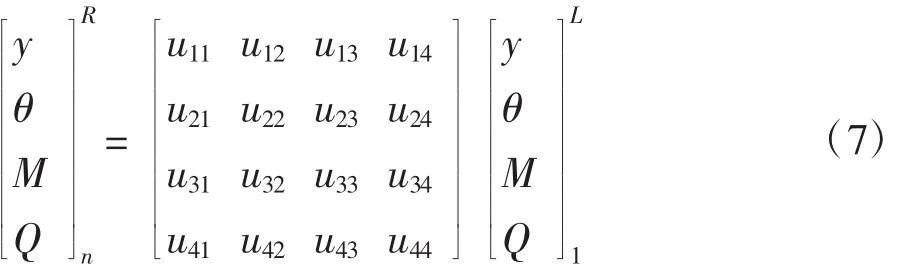
由圖3（a）及材料力學可得第i梁段的左端與第i-1梁段右端狀態變量的傳遞關系：

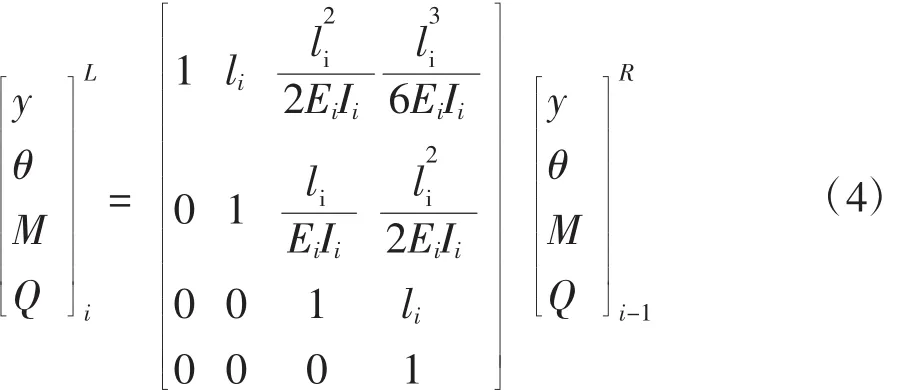
因疲勞加載試驗采取共振的方式，求解葉片振動系統的固有頻率時不考慮激振力。由圖3（b）忽略激振力Ff，非激振點的第i質量左右兩側狀態變量的傳遞關系為：=0，代入式（8）得到：采用普勞爾法或借助計算機可求解出式（9）中的固有圓頻率ω，進而得到該固有頻率的主振型。

由齊次方程組有非零解的條件得：

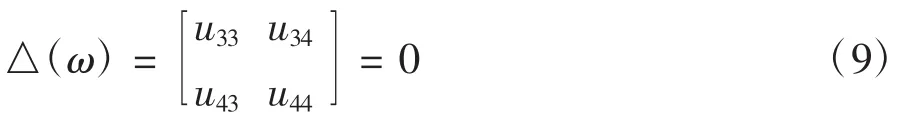
假設激振力加載位置為集中質量的質心處，由圖3（b）可得特定激振點f左右兩側剪力Qi的傳遞關系：

則激振點f左右兩側狀態變量的傳遞關系為：

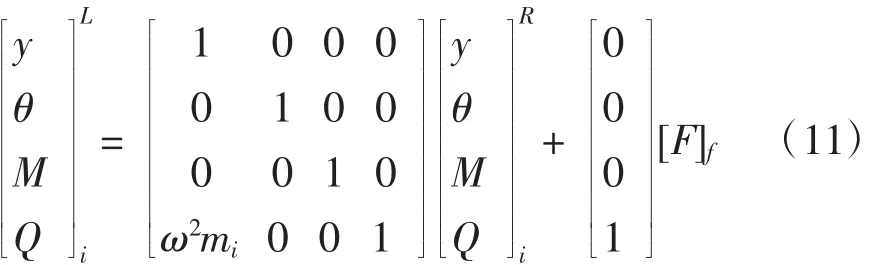
已知圓頻率ω、集中質量mi、截面剛度EiIi和各分段長度 li，由式（4）、（5）和（11），可得受迫振動系統的各分段的撓度yi、轉角θi、剪力Qi和彎矩Mi狀態量。

2.3 葉片振動系統激振力分析

根據IEC61400-23規范[3]，疲勞加載試驗時葉片展向上的彎矩分布要盡可能接近設計載荷彎矩，一般情況下，優先保證彎矩分布接近目標彎矩。為此通常在葉片不同位置上添加質量塊，與葉片共同組成振動系統。

根據工程試驗的需要，彎矩誤差δ按實際情況取值。假設特定截面j添加的質量塊質量為mj，則第j截面的集中質量總和為mi+mj.通常，直線驅動裝置控制質量塊相對于葉片做往復簡諧振動，產生余弦規律變化的激振力對葉片進行加載，假設激振力Ff（t）=Ffcos（ωt+ φ），即激振力的幅值 Ff＝ mjSω2，mj為激振點運動質量塊質量，S為運動質量塊行程。對于單點慣性式加載，以葉片為參考系，質量塊的位移為ym（t）=S cos（ωt）；葉片的位移為 y（t）=Yisin（ωt），Yi為激振點的撓度；則以地面為參考系，質量塊的位移為ym（t）+y（t） =S cos（ωt） +Yisin（ωt）.

可求得激振力一個周期能量輸入為：

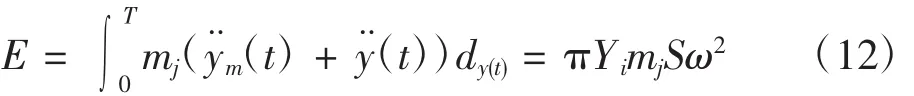
由 Ff=mjSω2可得：

當葉片在激振力的作用下運動時，在一個振動周期內所有離散段質量的動能為：

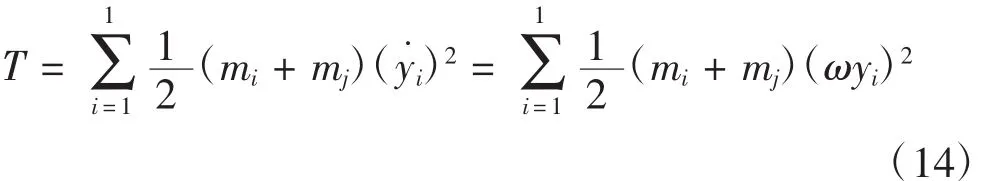
由此可以推導得到：

由式（13）和式（15）可求得激振力：

上式表達了單點激振力和動能的關系[4]，葉片在多點激振力作用下同樣要滿足動能關系式，則式（17）推及至多點激振，有如下表達式：

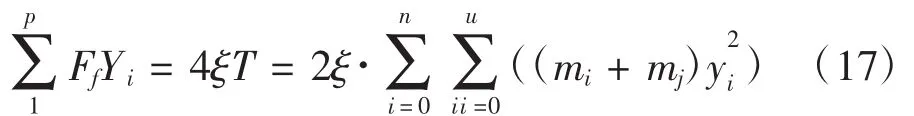
上式中：p表示激振點的個數，例如兩點加載時p=2；Yi為激振點的撓度；yi為各分段截面撓度。

已知試驗葉片n分段的集中質量mi、截面剛度EiIi、分段長度li及目標彎矩分布，激振力的求解步驟如下：

（1）對于試驗葉片，在未添加配重質量情況下，通過傳遞矩陣法分析試驗葉片的模態，并設定試驗頻率的下限值；

（2）選取適當的激振及配重塊添加位置，根據目標彎矩的分布，通過傳遞矩陣法，求能滿足誤差δ的匹配質量mj，并確定此時葉片振動系統的固有頻率ω.求解的約束條件為葉片振動系統的固有頻率高于步驟1設定的下限值，最優目標函數為添加的質量塊總和最小。當難以求得滿足條件的配重質量時，彎矩包絡范圍可適量縮小，后續通過激振力調節彎矩包絡范圍；

（3）對于單點激振，通過傳遞矩陣法，可計算使得彎矩完全滿足誤差δ和滿足式（15）的激振力；

（4）對于多點激振，還需要考慮各點激振力的分配問題，借助計算機對多個激振力的分配方案尋優，約束條件為滿足目標彎矩誤差δ和式（16），最優目標函數為彎矩誤差δ最小。

3 多點激振加載方案算例

對某型56.5m的葉片進行揮舞方向疲勞加載試驗，為了降低阻尼在試驗前將葉片尖部截斷，剩余的試驗葉片長度為48m，根據實際需要，彎矩包絡范圍設定為8m～32m，彎矩誤差δ為+10%，設計單點與多點激振方案，其中多點激振以兩點激振為例。兩點激振相比于單點，可使用兩個質量較小的激振器同時激振。兩個激振器的框架質量相同，運動質量可以不同，因此兩個激振器的總質量可以不同。根據以上建模方法，可得到單點及兩點激振的疲勞加載方案如表1，彎矩包絡曲線如圖4.將兩點激振與單點激振疲勞加載試驗方案進行對比，如表2所示。

表1 單點與兩點激振方案

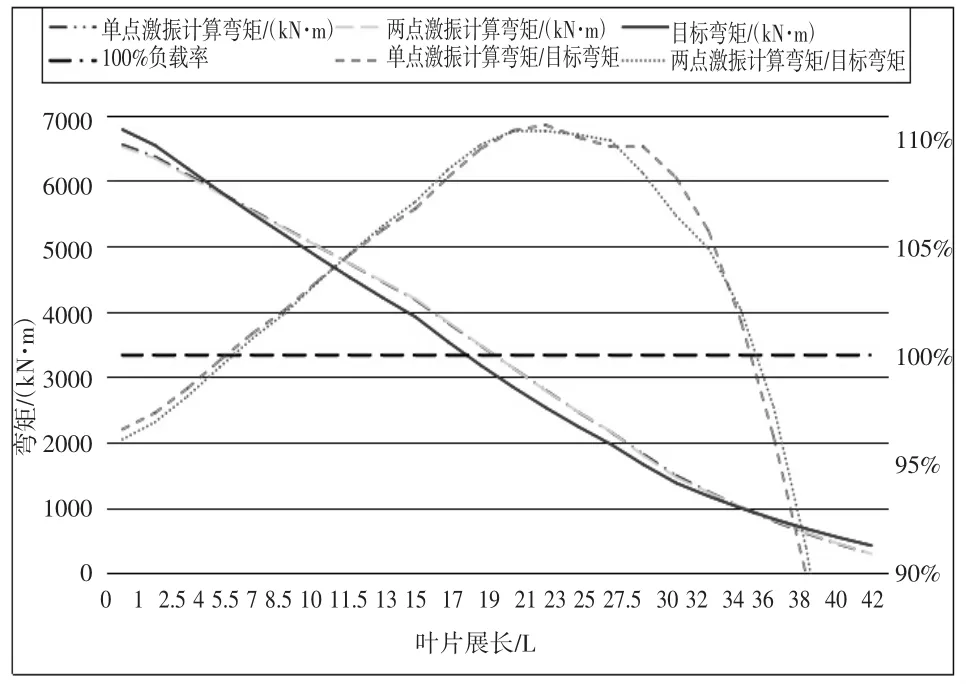
圖4 兩點激振方案彎矩曲線

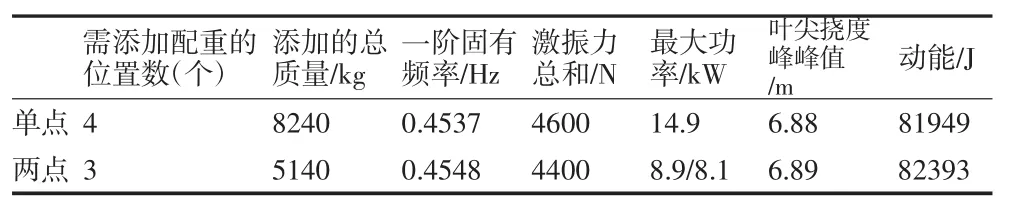
表2 兩點激振與單點激振方案對比

4 結束語

本文通過對風機葉片多點疲勞加載系統進行振動模型分析，從激振力和彎矩匹配的角度設計加載方案。通過方案對比，可知葉片多點激振疲勞加載試驗，激振力可替代部分質量塊的質量來調整彎矩分布，相較于單點激振可靈活調整疲勞試驗彎矩分布，使得彎矩更均勻，包絡范圍增大，且添加的總質量較小，葉片振動系統一階固有頻率升高，有利于增大激振力，減少疲勞試驗周期，提高試驗平臺的利用率。同時隨著風機葉片的大型化，多點激振可滿足大尺寸葉片疲勞試驗的要求。

[1]沈 宏，耿 超，劉 楠，等.國內外風電產業現狀及其發展前景[J].河南科技學院學報（自然科學版），2010，38（01）：97-101.

[2]廖高華，烏建中，張 豪.風電葉片雙慣性激振疲勞加載耦合振動特性[J].同濟大學學報（自然科學版），2017，45（07）：1016-1021.

[3]IEC TS 61400-23-2010，Wind turbines generator systems Part 23：Full scale structural testing of rotor blades[S]．

[4]樂韻斐，駱永云，劉 宇.風電機組葉片疲勞加載試驗減阻尼器結構優化設計[J].風能，2017（02）：96-98.