邊標志算法中常見問題及解決方法

摘 要

本文針對傳統的邊標志算法在遇到水平邊、狹長條以及極值點等情況時會出現錯誤填充的現象，提出了一種新的改進方法。改進后的算法需要設置一個計量型變量label，訪問到一個像素點時將該像素點的label值加1，以完全區別邊界點與內點。實驗結果表明，改進后的算法對上述問題僅使用標記值加1的簡單操作便能夠有效的處理，使得改進之后的算法在圖形圖像數據處理以及多媒體通信等范圍內取得更加廣泛的適用基礎。

【關鍵詞】邊標志算法 計算機圖形學 掃描轉換 區域填充

1 引言

多邊形填充是計算機圖形學中最基本的算法之一，而邊標志算法是多邊形填充算法中一種非常簡單容易描述的算法。在掃描的過程中設置一個布爾變量Label表示當前點的狀態，其初始值為假，對于每一個掃描范圍內的像素點如果是多邊形邊界上的點，便將Label的值取反，當Label的值為真時，便將當前像素點填充為填充色。

邊標志算法的這種思想是基于如矩形、橢圓等理想化規則圖形才能正確無誤的實現。但是在實際應用中，由于計算機硬件設備的限制以及現實生活中各種圖形的特點，該算法在離實際應用還有一定的距離。本文在深刻理解現有的邊標志算法的基礎上，對算法在實現過程中可能出現的問題進行分析，并給出一種相對簡單的解決方法。

2 算法的缺陷

2.1 極值點問題

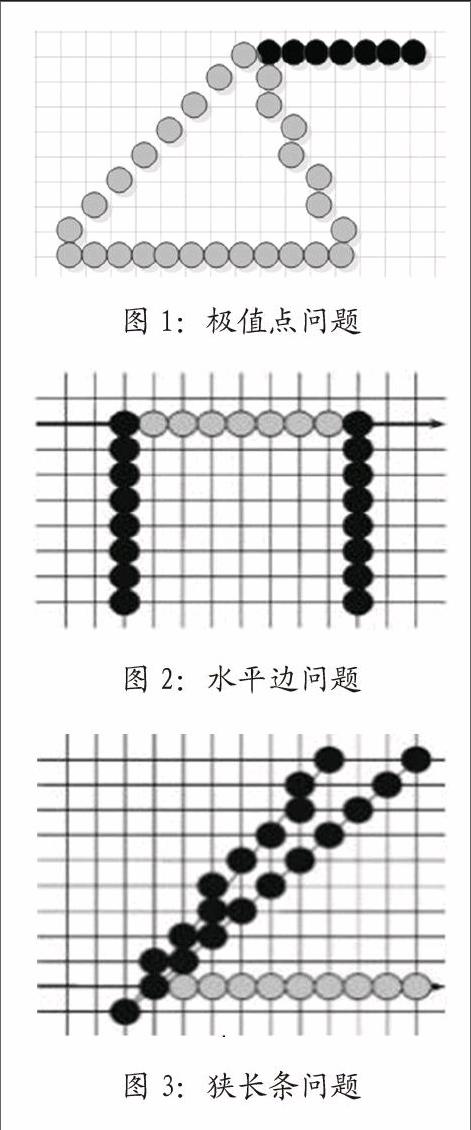
多邊形的頂點同時屬于兩條邊，但是并不是所有的頂點都會出現錯誤填充的現象。如果頂點不屬于極值點，則填充正常；否則在進行掃描填充時會使變量Label的值一直為真，從而出現該點右側出現“拖尾”現象。如圖1所示。

2.2 水平邊問題

當水平直線的像素點個數為偶數時，不會影響填充效果；當像素點個數為奇數時，就會出現填充錯誤，如圖2所示。

2.3 多邊形邊界線掃描轉換時的問題

邊標志算法實現的第一步是對多邊形的邊界線做上標記，但是這種情況在遇到邊界線斜率的絕對值小于1時，直線與同一掃描線之間的交點個數就有可能出現奇數，因此這種情況仍然會出現類似水平邊問題的填充異常現象。

2.4 狹長條問題

當兩條相交直線的斜率非常接近時，其交點在數字顯示器上的交點便會出現多個像素點，這時頂點附近的若干個像素點同樣也會重合，與水平掃描線之間的連續交點個數也有可能出現奇數。因此，在進行填充時同樣會出現類似于水平邊問題的填充異常現象，如圖3所示。

3 算法的改進

對上述問題深入分析，可以發現之所以會出現填充異常現象，是因為傳統的邊標志算法沒有將普通的邊界點與上述問題中的像素點區別開來。本文提出的新的改進方法的主要思想為：在對多邊形的每一條邊進行光柵化時，使用label（初始值為0）標記是否為多邊形的邊界，首先存儲單元中取出當前像素點的label值，然后對當前需要標記的像素點的label值進行加1，然后在存放到當前像素點的label值的位置。依次對對每一條邊進行光柵化。在對多邊形內部區域進行填充時，起先讀出當前像素點的label值，當前像素點的label值若是1，則讀取當前像素點的水平方向的左側和右側像素點的label值，如果他們的值都為1，則布爾變量inner的值不變，否則取反。填充顏色時若當前像素點的label值大于0或者inner為真時，則填充為填充色，不然填充為背景色。如對于圖1中的A點和B點，在對兩點所在邊界光柵化之后他們的label值等于2是大于1的，所以在填充顏色時將A和B點填充為填充色。又因為其前后兩個像素點的label值不都為1，所以inner的值仍為假，從而該點右邊的像素點不填充。

4 驗證

通過多次實驗的驗證可以發現，改進之后的算法避免了在掃描填充時反復調用邊表結構的問題，僅僅使用對邊界像素點的標記值加1的操作即可實現上述問題中多邊形的正常填充。無論從硬件實現還是從軟件實現，改進后的邊標志算法比原來算法在運行效率上都有相當的提高。

參考文獻

[1]D.F.羅杰斯（梁友棟，石教英，彭群生譯）.計算機圖形學的算法基礎[M].北京：科學出版社，1987.

[2]張志龍，李吉成，沈振康.一種新的快速復雜連通區域掃描線填充算法[J].計算機工程與應用，2004，40（31）：6-8.

[3]吳章文，楊代倫，勾成俊，等.區域填充極點判別算法[J].計算機輔助設計與圖形學學報，2003，15（08）：979-983.

作者簡介

王利祥（1987-），男，河南省濮陽市人。碩士學位。主要研究方向為電子與通信工程、嵌入式計算。

作者單位

河南護理職業學院網絡管理中心 河南省安陽市 455000