非連通圖2D3，4∪G的優美標號

吳躍生

（華東交通大學理學院，江西南昌330013）

非連通圖2D3，4∪G的優美標號

吳躍生

（華東交通大學理學院，江西南昌330013）

討論了非連通圖2D3，4∪G的優美性，給出了非連通圖D3，4∪G是優美圖的二十一個充分條件.證明了非連通圖2D3，4∪G(k)+a（a=2，3，4，5，6，8，9，…，23）都是優美的.

優美圖；交錯圖；非連通圖；優美標號

引言

記號[m，n]表示整數集合{m，m＋1，…，n}，m和n均為非負整數，且滿足0≤m＜n.記號G(k)+m表示圖G是特征為k且缺k＋m標號值的交錯圖.本文所討論的圖均為無向簡單圖，記號V（G）和E（G）分別表示圖G的頂點集和邊集，未說明的符號及術語均同文獻[1-17].

圖的優美標號問題是組合數學中一個熱門課題[1-17].

1 概念

定義1[1]對于一個圖G=（V，E），稱G是優美圖，θ是G的一組優美標號是指：如果存在一個單射使得對所有邊e=uv∈E（G），由導出的映射是一個雙射.

定義2[2]設θ是圖G的優美標號，V（G）=X∪Y，且X∪Y=Φ，如果，則稱θ是G的交錯標號.稱G是在交錯標號θ下的交錯圖.稱k為交錯圖G關于交錯標號θ的特征.

把任意m個圈Cn的恰有一個公共點所組成的圖記作Dm，n[1].

非連通圖2D3，4存在特征為12，且缺6，14，15，22和23標號值的交錯標號，如圖1所示，為方便記，把如圖1所示的標號記為：（13；9，21，10；12，19，11；8，17，7）；（24；3，16，2；0，18，1；4，20，5）；

非連通圖2D3，4存在特征為11，且缺1，2，9，10和18標號值的交錯標號，如圖2所示，為方便記，把如圖2所示的標號記為：（11；15，3，4；12，5，13；16，7，17）；（0；21，8，22；24，6，23；20，4，19）；本文討論了非連通圖2D3，4∪G的優美性.

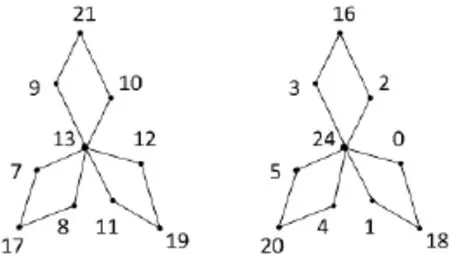
圖1 非連通圖2D3，4的交錯標號

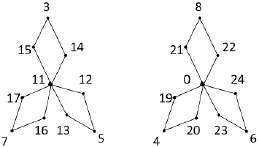
圖2 非連通圖2D3，4的交錯標號

2 主要結果及其證明

（1）特征為k＋14且缺k＋1，k＋8，k＋16，k＋17和k＋20標號值的交錯標號；

（2）特征為k＋14且缺k＋1，k＋8，k＋16，k＋17和k＋24標號值的交錯標號.

證設2D3，4如圖2所示，設X，Y是圖G(k)＋2的一個二分化，θ1是圖G(k)＋2的交錯標號，且

圖3 非連通圖2D3，4

非連通圖2D3，4∪G(k)+2的各種頂點標號θ定義為：

第一種標號：θ（x1）=k＋15，θ（x2）=k＋12，θ（x3）=k＋23，θ（x4）=k＋11，θ（x5）=k＋14，θ（x6）=k＋21，θ（x7）=k＋13，θ（x8）=k＋10，θ（x9）=k＋19，θ（x10）=k＋9，簡記為（下文同）：（k＋15；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）.

θ（y1）=k＋24，θ（y2）=k＋5，θ（y3）=k＋18，θ（y4）=k＋4，θ（y5）=k＋3，θ（y6）=k＋26，θ（y7）=k＋2，θ（y8）=k＋7，θ（y9）=k＋22，θ（y10）=k＋6.簡記為（下文同）：

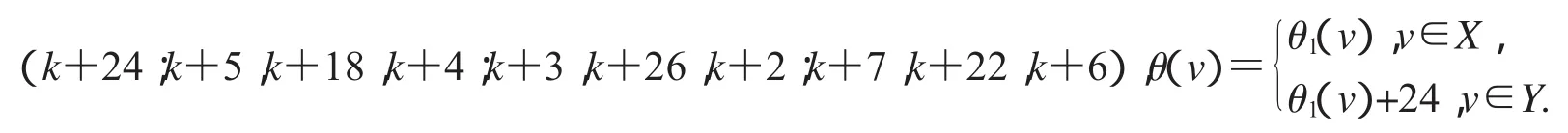
第二種標號：（k＋15；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）；

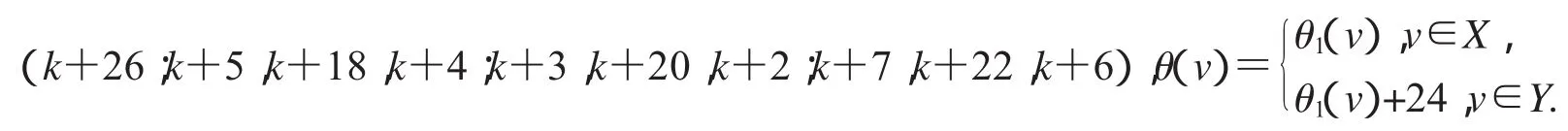
下面證明第一種標號θ是非連通圖2D3，4∪G(k)＋2的優美標號.

（1）θ：X→[0，k]是單射；θ：Y→[k＋25，q＋24]－{k＋26}是單射；

θ：V（2D3，4）→[k＋2，k＋24]∪{k＋26}－{k＋8，k＋16，k＋17，k＋20}是雙射；

有θ：V（2D3，4∪G(k)+2）→[0，q＋24]－{k＋1，k＋8，k＋16，k＋17，k＋20}是單射.

θ'：E（2D3，4）→[1，24]是雙射；

θ'：E（G(k)＋2）→[25，q＋24]是雙射.

θ'：E（2D3，4∪G(k)＋2）→[1，q＋24]是一一對應.

由（1）和（2）可知第一種標號θ就是非連通圖2D3，4∪G(k)+2的缺k＋1，k＋8，k＋16，k＋17和k＋20標號值的優美標號.

令X1=X∪{x2，x4，x5，x7，x8，x10}∪{y2，y4，y5，y7，y8，y10}，

Y1=Y∪{x1，x3，x6，x9}∪{y1，y3，y6，y9}，

所以，第一種標號θ就是非連通圖D2，4∪G(k)＋2的特征為k＋14，且缺k＋1，k＋8，k＋16，k＋17和k＋20標號值的交錯標號.

其他各種標號的證明可仿上.證畢.

以下定理只給出標號，定理證明與定理1的第一種標號證明過程類似，故省略.

設2D3，4如圖2所示，設X，Y是圖G(k)＋3的一個二分化，θ1是圖G(k)＋3的交錯標號，且

非連通圖2D3，4∪G(k)＋3的頂點標號θ定義為：

設2D3，4如圖2所示，設X，Y是圖G(k)＋4的一個二分化，θ1是圖G(k)＋4的交錯標號，且

非連通圖2D3，4∪G(k)＋4的頂點標號θ定義為：

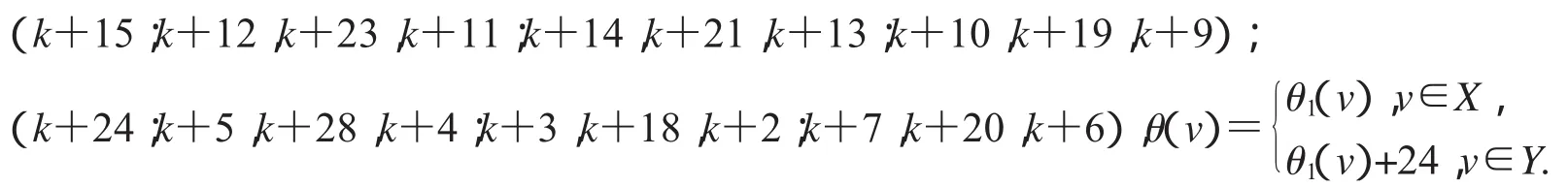
設2D3，4如圖2所示，設X，Y是圖G(k)＋5的一個二分化，θ1是圖G(k)＋5的交錯標號，且

非連通圖2D3，4∪G(k)＋5的頂點標號θ定義為：

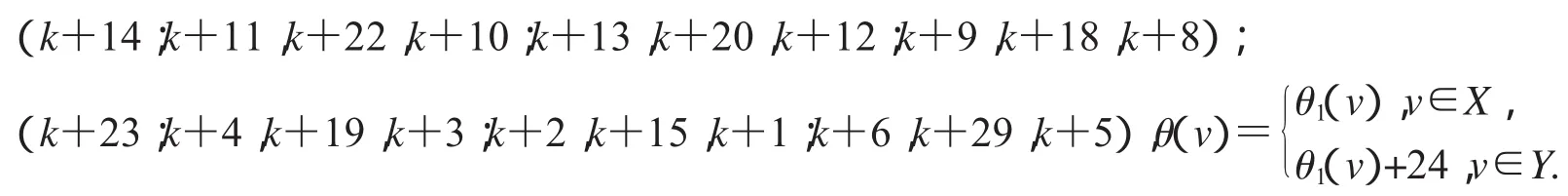
設2D3，4如圖2所示，設X，Y是圖G(k)＋6的一個二分化，θ1是圖G(k)＋6的交錯標號，且

非連通圖2D3，4∪G(k)＋6的頂點標號θ定義為：

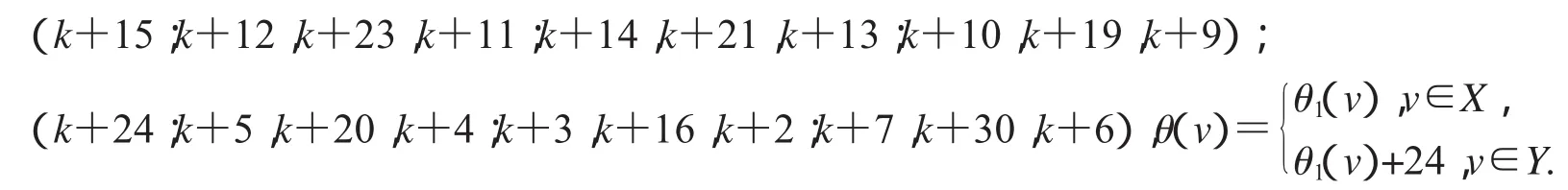
（1）特征為k＋13且缺k＋7，k＋16，k＋20，k＋21和k＋24標號值的交錯標號；

（2）缺k＋14，k＋15，k＋16，k＋23和k＋24標號值的交錯標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋8的一個二分化，θ1是圖G(k)＋8的交錯標號，且

非連通圖2D3，4∪G(k)＋8的各種頂點標號θ定義為：

第一種標號為：（k＋14；k＋11，k＋18，k＋10；k＋13，k＋22，k＋12；k＋9，k＋32，k＋8）；

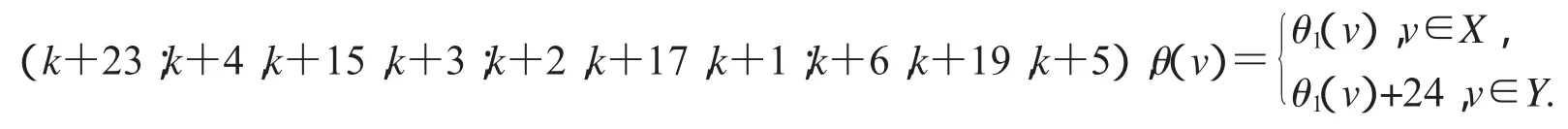
第二種標號為：（k＋32；k＋11，k＋22，k＋10；k＋13，k＋20，k＋12；k＋9，k＋18，k＋8）；

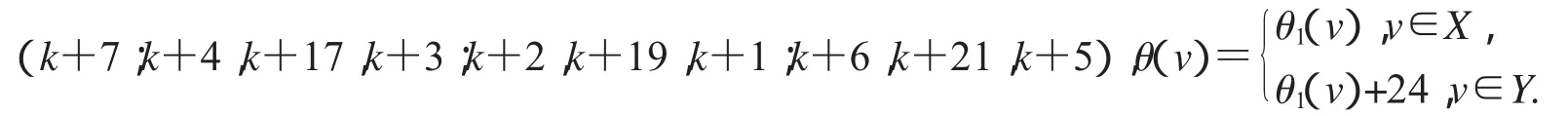
（1）特征為k＋14且缺k＋1，k＋8，k＋17，k＋21和k＋22標號值的交錯標號.

（2）缺k＋1，k＋15，k＋16，k＋17和k＋24標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋9的一個二分化，θ1是圖G(k)＋9的交錯標號，且

非連通圖2D3，4∪G(k)＋9的各種頂點標號θ定義為：

第一種標號為：（k＋15；k＋12，k＋19，k＋11；k＋14，k＋23，k＋13；k＋10，k＋33，k＋9）；

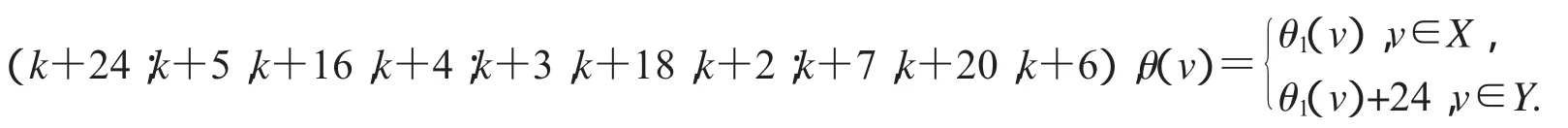
第二種標號為：（k＋33；k＋12，k＋23，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9）；

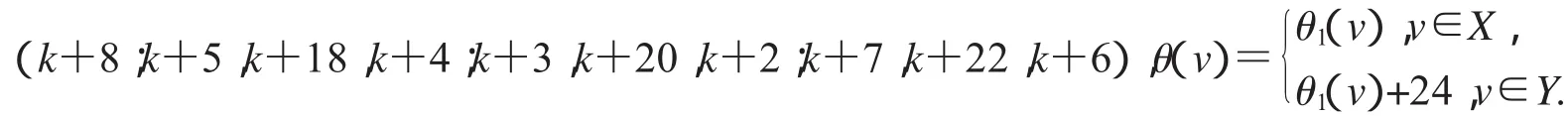
（1）特征為k＋13且缺k＋7，k＋16，k＋21，k＋22和k＋24標號值的交錯標號；

（2）缺k＋1，k＋2，k＋16，k＋17和k＋18標號值的優美標號；

（3）缺k＋7，k＋8，k＋9，k＋23和k＋24標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋10的一個二分化，θ1是圖G(k)＋10的交錯標號，且

非連通圖2D3，4∪G(k)＋10的各種頂點標號θ定義為：

第一種標號為：（k＋14；k＋11，k＋34，k＋10；k＋13，k＋20，k＋12；k＋9，k＋18，k＋8）；

第二種標號為：（k＋34；k＋13，k＋24，k＋12；k＋15，k＋22，k＋14；k＋11，k＋20，k＋10）；

第三種標號為：（k＋34；k＋13，k＋1，k＋12；k＋11，k＋3，k＋10；k＋15，k＋5，k＋14），

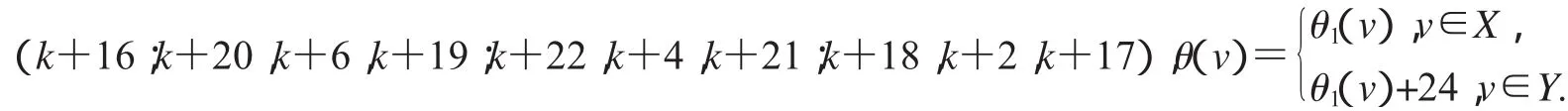
（1）特征為k＋14且缺k＋1，k＋8，k＋17，k＋22和k＋23標號值的交錯標號；

（2）缺k＋2，k＋3，k＋6，k＋17和k＋24標號值的優美標號；

（3）缺k＋1，k＋8，k＋9，k＋10和k＋24標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋11的一個二分化，θ1是圖G(k)＋11的交錯標號，且

非連通圖2D3，4∪G(k)＋11的各種頂點標號θ定義為：

第一種標號為：（k＋15；k＋12，k＋35，k＋11；k＋14，k＋21，k＋13；k＋10，k＋19，k＋9），

第二種標號為：（k＋10；k＋14，k＋4，k＋13；k＋12，k＋35，k＋11；k＋16，k＋8，k＋15），

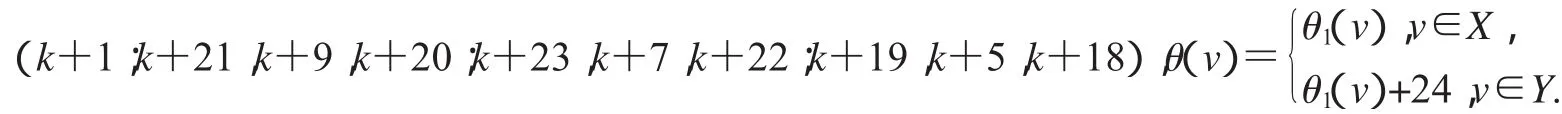
第三種標號為：（k＋35；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

（1）特征為k＋13且缺k＋7，k＋18，k＋21，k＋22和k＋24標號值的交錯標號；

（2）缺k＋1，k＋3，k＋4，k＋7和k＋18標號值的優美標號；

（3）缺k＋1，k＋2，k＋9，k＋10和k＋11標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋12的一個二分化，θ1是圖G(k)＋12的交錯標號，且

非連通圖2D3，4∪G(k)＋12的各種頂點標號θ定義為：

第一種標號為：（k＋14；k＋11，k＋20，k＋10；k＋13，k＋36，k＋12；k＋9，k＋16，k＋8），

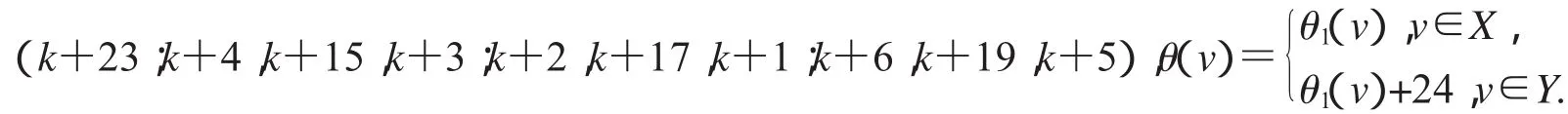
第二種標號為：（k＋11；k＋15，k＋5，k＋14；k＋13，k＋36，k＋12；k＋17，k＋9，k＋16），

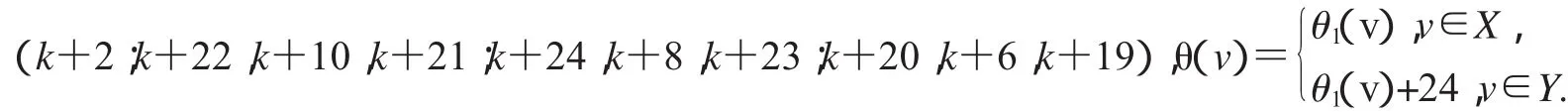
第三種標號為：（k＋36；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

（1）特征為k＋14且缺k＋1，k＋8，k＋19，k＋22和k＋23標號值的交錯標號；

（2）缺k＋2，k＋3，k＋8，k＋17和k＋24標號值的優美標號；

設2D3，4如圖2所示，設X，Y是圖G(k)＋13的一個二分化，θ1是圖G(k)＋13的交錯標號，且

非連通圖2D3，4∪G(k)＋13的各種頂點標號θ定義為：

第一種標號為：（k＋15；k＋12，k＋21，k＋11；k＋14，k＋37，k＋13；k＋10，k＋17，k＋9），

第二種標號為：（k＋10；k＋14，k＋37，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

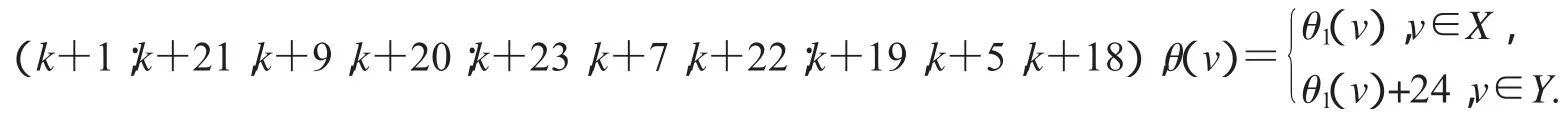
設2D3，4如圖2所示，設X，Y是圖G(k)＋14的一個二分化，θ1是圖G(k)＋14的交錯標號，且

非連通圖2D3，4∪G(k)＋14的頂點標號θ定義為：

（k＋11；k＋15，k＋38，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

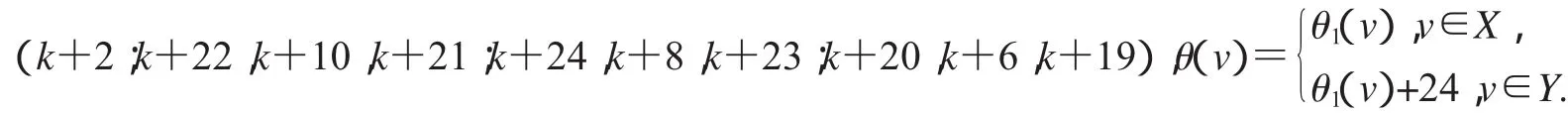
設2D3，4如圖2所示，設X，Y是圖G(k)＋15的一個二分化，θ1是圖G(k)＋15的交錯標號，且

非連通圖2D3，4∪G(k)＋15的頂點標號θ定義為：

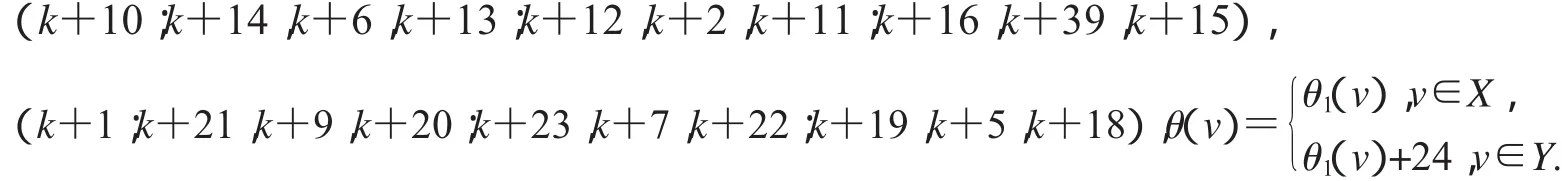
設2D3，4如圖2所示，設X，Y是圖G(k)＋16的一個二分化，θ1是圖G(k)＋16的交錯標號，且

非連通圖2D3，4∪G(k)＋16的頂點標號θ定義為：

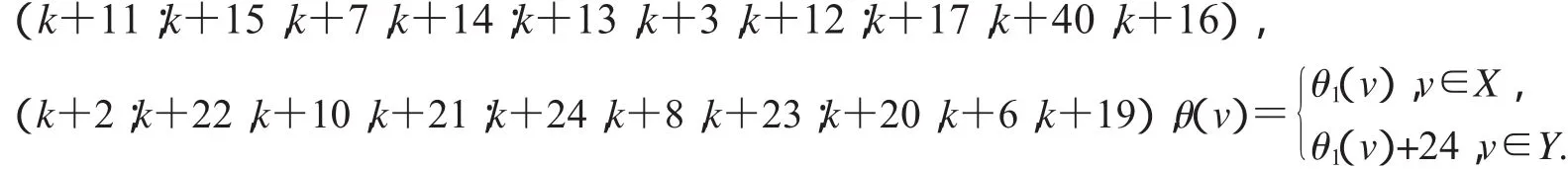
設2D3，4如圖2所示，設X，Y是圖G(k)＋17的一個二分化，θ1是圖G(k)＋17的交錯標號，且

非連通圖2D3，4∪G(k)＋17的頂點標號θ定義為：

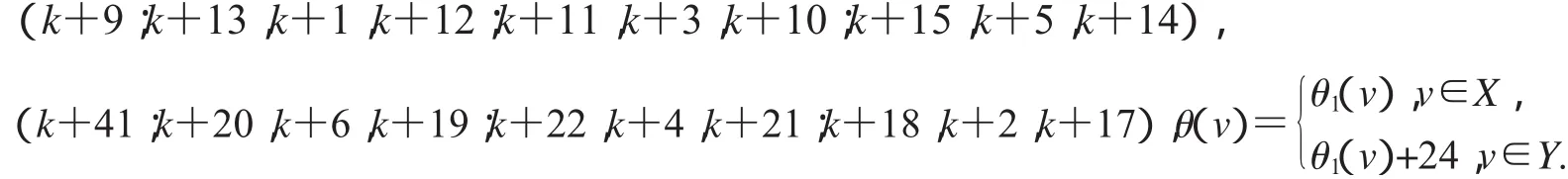
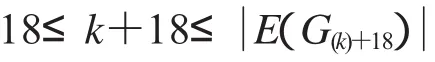
定理16當時，非連通圖2D3，4∪G(k)＋18存在

（1）缺k＋3，k＋7，k＋8，k＋17和k＋24標號值的優美標號；

（2）缺k＋6，k＋14，k＋15，k＋22和k＋23標號值的優美標號；

（3）缺k＋1，k＋8，k＋9，k＋17和k＋24標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋18的一個二分化，θ1是圖G(k)＋18的交錯標號，且

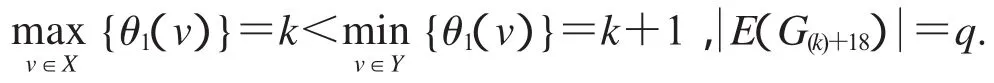
非連通圖2D3，4∪G(k)＋18的各種頂點標號θ定義為：

第一種優美標號：（k＋10；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

第二種優美標號：（k＋13；k＋10，k＋21，k＋9；k＋12，k＋19，k＋11；k＋8，k＋17，k＋7），

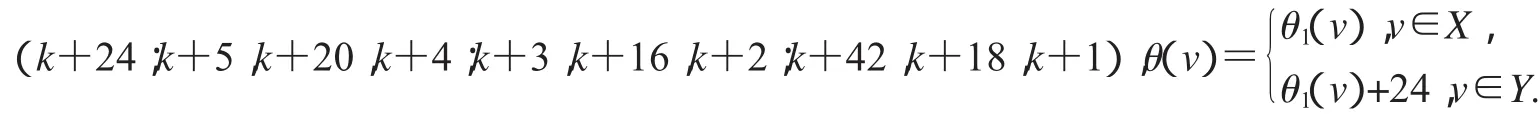
第三種優美標號：（k＋10；k＋14，k＋2，k＋13；k＋12，k＋4，k＋11；k＋16，k＋6，k＋15），

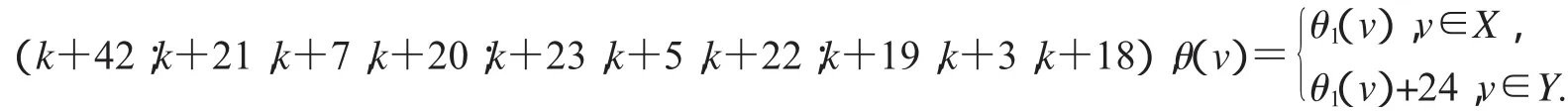
（1）缺k＋1，k＋4，k＋8，k＋9和k＋18標號值的優美標號；

（2）缺k＋1，k＋2，k＋9，k＋10和k＋18標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋19的一個二分化，θ1是圖G(k)＋19的交錯標號，且

非連通圖2D3，4∪G(k)＋19的各種頂點標號θ定義為：

第一種優美標號：（k＋11；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

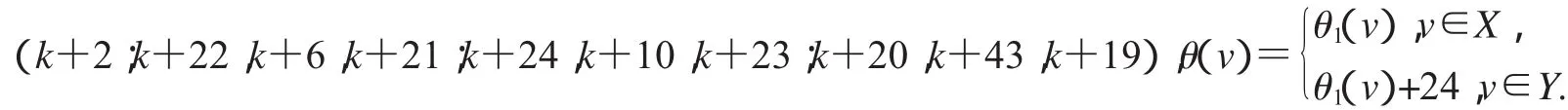
第二種優美標號：（k＋11；k＋15，k＋3，k＋14；k＋13，k＋5，k＋12；k＋17，k＋7，k＋16），

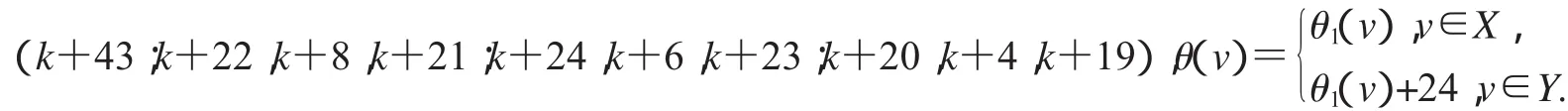
設2D3，4如圖2所示，設X，Y是圖G(k)＋20的一個二分化，θ1是圖G(k)＋20的交錯標號，且

非連通圖2D3，4∪G(k)＋20的頂點標號θ定義為：

設2D3，4如圖2所示，設X，Y是圖G(k)＋21的一個二分化，θ1是圖G(k)＋21的交錯標號，且

非連通圖2D3，4∪G(k)＋21的頂點標號θ定義為：

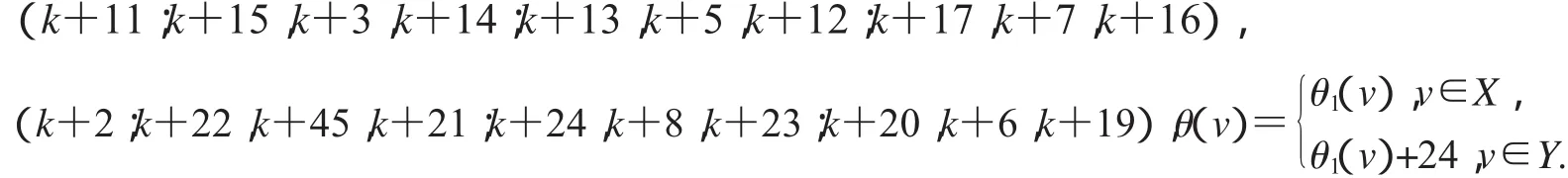
設2D3，4如圖2所示，設X，Y是圖G(k)＋22的一個二分化，θ1是圖G(k)＋22的交錯標號，且

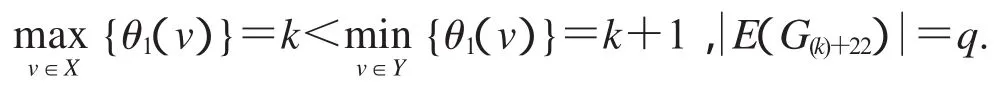
非連通圖2D3，4∪G(k)＋22的頂點標號θ定義為：

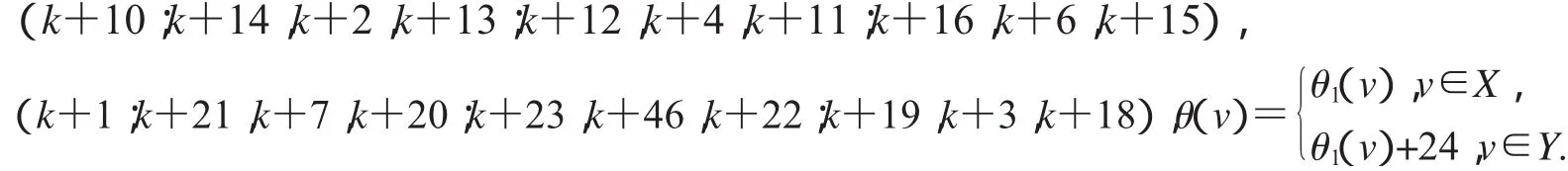
定理21當時，非連通圖2D3，4∪G(k)＋23存在缺k＋1，k＋6， k＋9，k＋10和k＋18標號值的優美標號.

設2D3，4如圖2所示，設X，Y是圖G(k)＋23的一個二分化，θ1是圖G(k)＋23的交錯標號，且

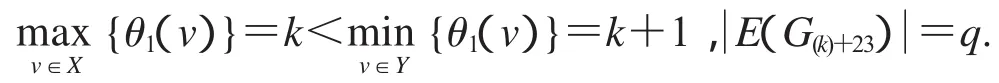
非連通圖2D3，4∪G(k)＋23的頂點標號θ定義為：

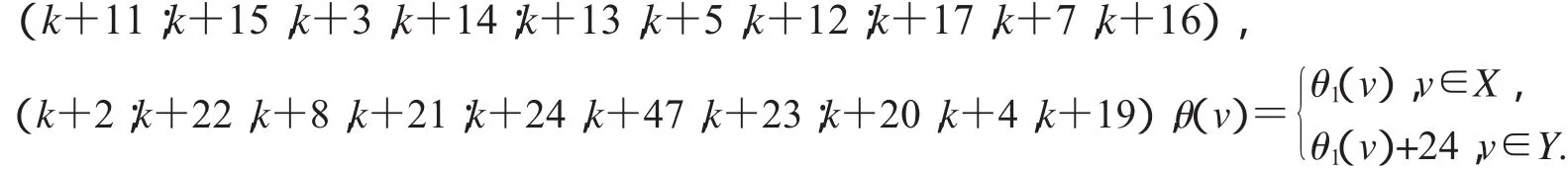
3 結論

本文討論了非連通圖2D3，4∪G的優美性，給出了非連通圖2D3，4∪G是優美圖的二十一個充分條件.證明了：非連通圖2D3，4∪G(k)＋a（a=2，3，4，5，6，8，9，…，23）都是優美的，可為繼續研究非連通圖sDm，n∪G的優美性提供借鑒.

[1]馬克杰.優美圖[M].北京：北京大學出版社，1991.

[2]楊顯文.關于C4m蛇的優美性[J].工程數學學報，1995，12（4）：108-112.

[3]GALLIANJA.Adynamicsurveyofgraphlabeling[J].TheElectronicJoumalofCombinatorics，2013，16，DS6.

[4]吳躍生，王廣富，徐保根.非連通圖C4m∪G的優美標號[J].重慶師范大學學報（自然科學版），2015，32（2）：79-83.

[5]吳躍生.非連通圖C4m-1∪G的優美標號[J].吉首大學學報（自然科學版），2014，35（3）：1-3.

[6]吳躍生.非連通圖D3，4∪G的優美性[J].唐山學院學報，2015，28（6）：3-6.

[7]吳躍生.非連通圖L6∪G的優美標號[J].西華大學學報（自然科學版），2015，34（2）：30-35.

[8]吳躍生.非連通圖3C4m∪C4m-1∪G的優美標號[J].蘭州大學學報（自然科學版），2015，51（1）：115-118.

[9]吳躍生.非連通圖2C4m∪C8m-1∪G的優美性[J].東北師范大學學報（自然科學版），2015，47（3）：60-63.

[10]吳躍生.基于路P8m＋4t＋2的交錯標號的圖S（4m+1，4（t+1），4m-1）的優美標號[J].中山大學學報（自然科學版），2015，54（5）：19-23.

[11]吳躍生，王廣富，徐保根.交錯圖的奇優美性和協調性[J].武漢大學（理學版），2014，60（6）：557-560.

[12]吳躍生.非連通圖C4m-1∪C4m∪G的優美標號[J].西南大學（自然科學版），2014，36（8）：83-86

[13]嚴謙泰.積圖Pn×Pm的奇優美性和奇強協調性[J].系統科學與數學，2010，30（3）：341-348.

[14]王濤，閏守峰，李德明.若干并圖的優美標號[J].數學的實踐與認識，2012，42（16）：201-212.

[15]劉信生，劉元元，姚兵，等.具有奇優美性的一類龍圖[J].西南大學學報（自然科學版），2014，36（4）：47-51.

[16]唐保祥，任韓.3類特殊圖的優美性[J].武漢大學學報（理學版），2014，60（6）：553-556.

[17]魏麗俠，張昆龍.幾類并圖的優美標號[J].中山大學學報（自然科學版），2008，47（3）：10-13.

Graceful Labeling of Unconnected Graph 2D3，4∪G

WU Yuesheng
（School of Science,East China JiaotongUniversity,Nanchang330013,Jiangxi,China）

The gracefulness of the unconnected graph 2D3，4∪G is discussed.Twenty-one sufficient conditions are given for the gracefulness of unconnected graph 2D3，4∪G.It is proved that the graph 2D3，4∪G(k)＋aare graceful graph for a=2，3，4，5，6，8，9，…，23

graceful graph;alternating graph;unconnected graph;graceful labeling

O157

A

1001-4217（2017）01-0053-10

2016-01-09

吳躍生（1959—），男，江西瑞金人，碩士，華東交通大學副教授，研究方向為優美標號.E-mail：616100567@qq.com.

國家自然科學基金項目（11261019，11361024）