二體旋轉庫侖衛(wèi)星編隊反饋線性化滑模控制

吳立堯，袁長清，施強

(空軍航空大學 飛行器與動力系，吉林 長春 130022)

二體旋轉庫侖衛(wèi)星編隊反饋線性化滑模控制

吳立堯，袁長清，施強

(空軍航空大學 飛行器與動力系，吉林 長春 130022)

為了減少在庫侖衛(wèi)星編隊運動過程中不確定因素的影響，避免控制過程中發(fā)生抖振現(xiàn)象，提高控制器的穩(wěn)定性、準確性，設計了適用于二體旋轉庫侖衛(wèi)星編隊的反饋線性化滑模控制方法。首先在地月系平動點L2點處附近建立二體旋轉庫侖衛(wèi)星編隊的動力學模型并進行簡化，針對庫侖編隊動力學特性，在滑模控制中加入了線性化反饋項，保證了編隊整體的魯棒性；仿真結果證明，該方法能夠使編隊達到預期構型，具有良好的控制性能。

庫侖衛(wèi)星編隊；平動點；反饋線性化；滑模控制；仿真；魯棒性

0 引言

近年來，關于近距離(10～100 m)衛(wèi)星編隊飛行的研究和應用成為了航天領域的研究熱點之一，King等[1]在2002年首次提出衛(wèi)星庫侖力編隊的概念以來，庫侖力編隊衛(wèi)星技術受到了廣泛關注。所謂庫侖力衛(wèi)星編隊技術，即控制衛(wèi)星的靜電荷量，通過設計適當的控制律改變航天器間相互作用靜電力來控制衛(wèi)星編隊的構型、姿態(tài)、距離等以完成預期任務。目前庫侖衛(wèi)星編隊飛行已成功應用到了SCATHA，ATS，CLUSTER任務中。

King和Parker[2]系統(tǒng)地研究了靜態(tài)庫侖編隊平衡電量和平衡位置的求解問題。基于Hill方程，利用編隊構形對稱性及圓形參考軌道條件，討論了靜態(tài)庫侖編隊平衡電量的存在性。Berryman和Schaub[3]提出一種求解靜態(tài)庫侖虛擬結構穩(wěn)態(tài)平衡電量的數值方法。之后兩人又利用非經典哈密爾頓庫侖衛(wèi)星動力學方程，通過將軌道運動和姿態(tài)運動解耦，提出了應用恒定電荷量實現(xiàn)靜態(tài)編隊的必要條件[4]。

對于庫侖編隊系統(tǒng)反饋控制問題，Hussein等[5]于2007年首次研究庫侖虛擬結構的反饋控制問題。考慮三結點共線虛擬結構，應用線性化相對動力學方程設計了電荷反饋控制律。Natarajan等[6-8]針對地球同步軌道的二體庫侖虛擬繩系編隊推導出衛(wèi)星的相對距離動力學方程和姿態(tài)動力學方程，并設計了電荷反饋控制器：文獻[6]在軌道徑向方向將非線性動力學方程線性化，設計了電荷PD反饋控制律來穩(wěn)定二體庫侖編隊構型；文獻[7]在軌道跡向方向和法線方向采用了推力器和庫侖力相結合的方式，設計了一個混合反饋控制律，并且沒有引起羽流問題；文獻[8]基于線性化平面外解耦模型，提出了一個只用庫侖力進行控制的控制律。Inampudi和Schaub等[9-10]針對于二體庫侖編隊在地月平動點處推導編隊動力學模型并設計了反饋控制律：文獻[9]利用拉格朗日方程推導出衛(wèi)星相對距離動力學方程和姿態(tài)動力學方程的一般式，設計電荷PD反饋控制律穩(wěn)定構型；文獻[10]考慮了環(huán)境力矩包括重力梯度力矩和太陽光壓攝動。Wang和Schaub[11]研究了地球同步軌道處兩衛(wèi)星自旋庫侖虛擬結構控制問題，設計全狀態(tài)反饋電荷控制器，并應用Lyapunov穩(wěn)定性理論，證明閉環(huán)系統(tǒng)是漸近穩(wěn)定的。

目前國內在靜態(tài)編隊以及動態(tài)編隊研究還比較少。王婷[12]分析了五星庫侖編隊飛行的靜態(tài)構型，并設計了線性二次型最優(yōu)控制律保持編隊穩(wěn)定。張皓和師鵬[13]在兩星問題結論的基礎上，通過對開環(huán)控制和閉環(huán)控制的仿真分析，給出了利用庫侖力技術實現(xiàn)懸停軌道的實施方案。黃靜[14]在Wang和Schaub[11]的基礎上解決了二星編隊在地月L2點附近的旋轉二體庫侖衛(wèi)星的相對運動控制問題。首先推導了限制性三體模型下二體衛(wèi)星在地-月系L2點附近的相對運動方程，進一步在抗飽和方法與反步法相結合的基礎上，設計了狀態(tài)限制輔助函數，解決了存在控制和狀態(tài)受限的衛(wèi)星相對運動變化并保持的虛擬結構控制問題。另外黃靜[15]針對于平動點附近處二體繩系系統(tǒng)姿軌耦合控制問題，首先采用歐拉-拉格朗日方程對二體衛(wèi)星建模，設計了非線性二次型最優(yōu)控制器實現(xiàn)了對二體繩系系統(tǒng)的長周期穩(wěn)定控制。

本文在Wang[11]的基礎上，考慮在深空環(huán)境下地月系平動點L2點附近情況下，兩衛(wèi)星自旋虛擬結構系統(tǒng)的相對運動控制問題。首先推導出限制性三體模型下二體庫侖衛(wèi)星在地月系平動點處附近處的相對運動方程，采用反饋線性化滑模變結構控制方法設計系統(tǒng)控制器，為系統(tǒng)提供了更好的動態(tài)特性，通過仿真驗證了該方法的可行性與優(yōu)點。

1 問題描述

1 .1 二體庫侖衛(wèi)星編隊動力學建模

如圖1為限制性三體問題下的二體庫侖衛(wèi)星系統(tǒng)，O為地月系的公共質心，Oxyz為以O為中心的慣性坐標系，地球與月球連線繞軸Oz以角速度ω轉動。令地球和月球的質量分別為M1和M2，2顆衛(wèi)星質量分別為m1和m2。

圖1 限制性三體問題下的二體庫侖衛(wèi)星系統(tǒng)Fig.1 Two-body coulomb satellite system

假設衛(wèi)星電勢小于自身等離子體動能，那么兩衛(wèi)星之間庫侖力作用在第1顆衛(wèi)星上可表示為

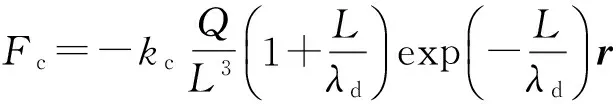
(1)

式中:kc為庫侖常數，大小為8.99×109C-2·N·m2；Q為兩帶電衛(wèi)星電荷乘積Q=q1q2，其中q1和q2分別為兩衛(wèi)星所帶電荷量；L為兩衛(wèi)星之間相對距離；λd為德拜長度(研究表明，在地球低軌道上，德拜長度僅為毫米至厘米量級；在地球同步軌道上，德拜長度為100～1 000 m；在深空環(huán)境中，德拜長度為20～50 m);r為第1顆衛(wèi)星指向第2顆衛(wèi)星的向量。

兩顆衛(wèi)星的慣性運動方程分別表示為

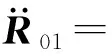
(2)

(3)

式中：R01和R02分別為兩顆衛(wèi)星在慣性坐標系中的位置向量；G是萬有引力常數，大小為G=6.674 28×10-11m3kg-1s-2；Rij分別為兩顆衛(wèi)星在慣性坐標系系下的相對于地球和月球的位置向量，如圖1所示。

由動力學方程(2)和(3)可得兩顆衛(wèi)星相對運動方程為

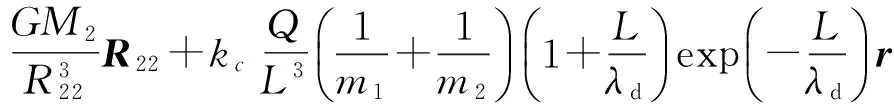
(4)

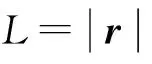
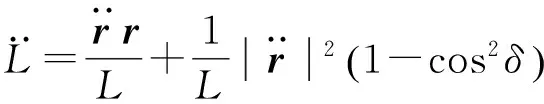
(5)

將式(4)代入式(5)可得到

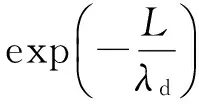
(6)

式中：與系統(tǒng)慣性位置向量相關的函數f1和與相對位置向量相關的函數f2分別為

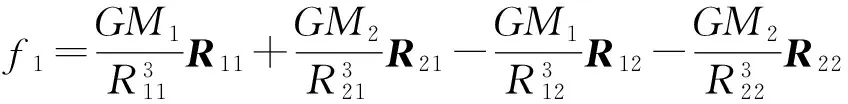
(7)

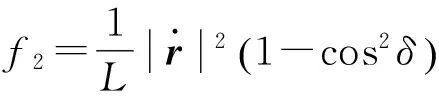
(8)

1.2 模型簡化

對于f1函數，在深空環(huán)境內(本文選取地月系平動點L2點處附近)，由于德拜效應的存在衛(wèi)星之間的距離不宜過大，為防止兩衛(wèi)星之間發(fā)生碰撞，衛(wèi)星之間距離也不宜過小，在本文中選取衛(wèi)星之間距離為10～40 m。在文獻[14]中，Wang證明了在地球同步軌道處，f1函數具有邊界值，且數量級遠小于f2。另外與庫侖力相比，數量級仍小于庫侖力。由于簡化f1函數過于繁瑣，此處在短期時間內可近似將f1視為干擾項。

對于f2函數，簡化過程如下：如圖2所示，Bereθeh為二體庫侖衛(wèi)星編隊系統(tǒng)的本體坐標系，其中er為方向為第1顆衛(wèi)星指向第2顆衛(wèi)星的單位向量，ωθ為兩星在本體坐標系內的旋轉角速度，eθ為ωθ角速度切線方向。利用如下式子：

(9)

式(5)中，根據余弦公式可得到

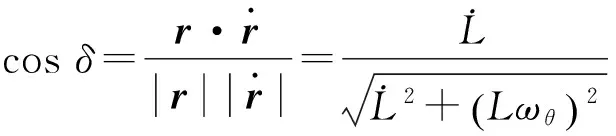
(10)

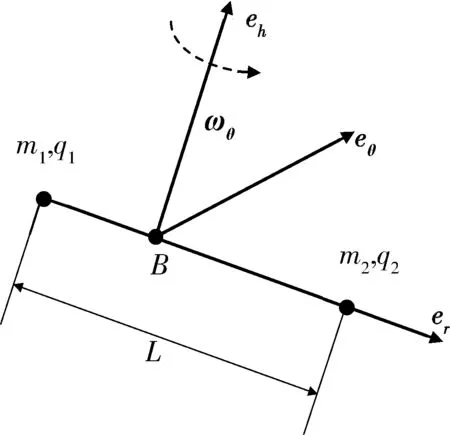
圖2 二體庫侖衛(wèi)星編隊系統(tǒng)的本體坐標系Fig.2 Body frame Bereθeh

在二體庫侖衛(wèi)星編隊高速自旋系統(tǒng)中，在短時間內，可忽略衛(wèi)星重力梯度力矩作用力，所以可近似看作系統(tǒng)角動量守恒，即

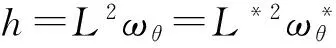
(11)

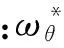
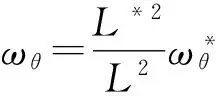
(12)

綜合式(8)，(10)和(12)可得

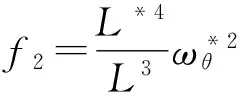
(13)

綜上所述，動力學方程(6)可近似為

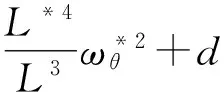
(14)

式中：d為包括f1函數與外界環(huán)境干擾(如太陽光壓所產生的干擾)。

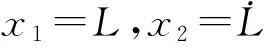
(15)

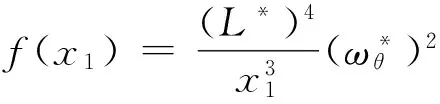
(16)

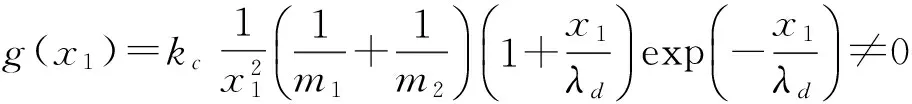
(17)

2 控制器設計

2.1 線性化反饋滑模控制

理想衛(wèi)星間距為xd，則間距誤差可表達為

e=x-xd.

(18)

設計滑模面函數為

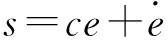
(19)

式中：c>0。

對滑模面函數求導可得

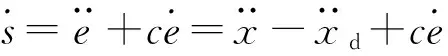
(20)

根據反饋線性化理論，設計滑模控制器為

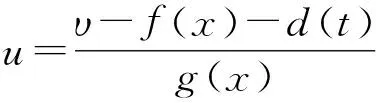
(21)

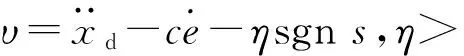
(22)

為防止在滑模控制過程中出現(xiàn)抖振現(xiàn)象，利用連續(xù)函數θ(s)取代符號函數sgns，則控制律式(21)可表達為

(23)

其中連續(xù)函數θ(s)為

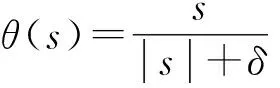
(24)

式中:δ表示邊界層厚度，為很小的正常數。

2.2 穩(wěn)定性分析

定義Lyapunov函數為

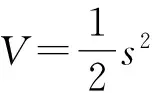
(25)

對式(25)進行求導可得到

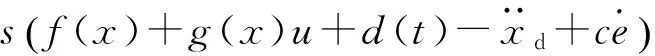
(26)

將控制律式(23)代入式(26)，可得到

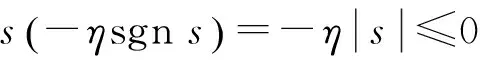
(27)

此時，控制器滿足Lyapunov穩(wěn)定性條件，系統(tǒng)可以在有限時間內到達滑模面。

3 仿真校驗

本節(jié)利用Matlab/Simulink對進行數值仿真，驗證在深空環(huán)境中兩星自旋庫侖編隊線性化反饋滑模控制律的有效性。

(28)

式中：r(t0)為慣性坐標系下相對位置向量。兩顆衛(wèi)星在慣性坐標系內初始速度為

(29)

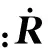
由于在地月系平動點處L2點處附近環(huán)境干擾非常小，主要由太陽光壓產生，數量級約為10-7N。在本文中假設干擾力約為[15]

d=5×10-7sin(ωst-γ)，

(30)

式中：ωs=2.462 9×10-6rad/s；γ為初始相位角，假設為15°。

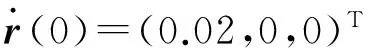
仿真結果如圖3～7所示。

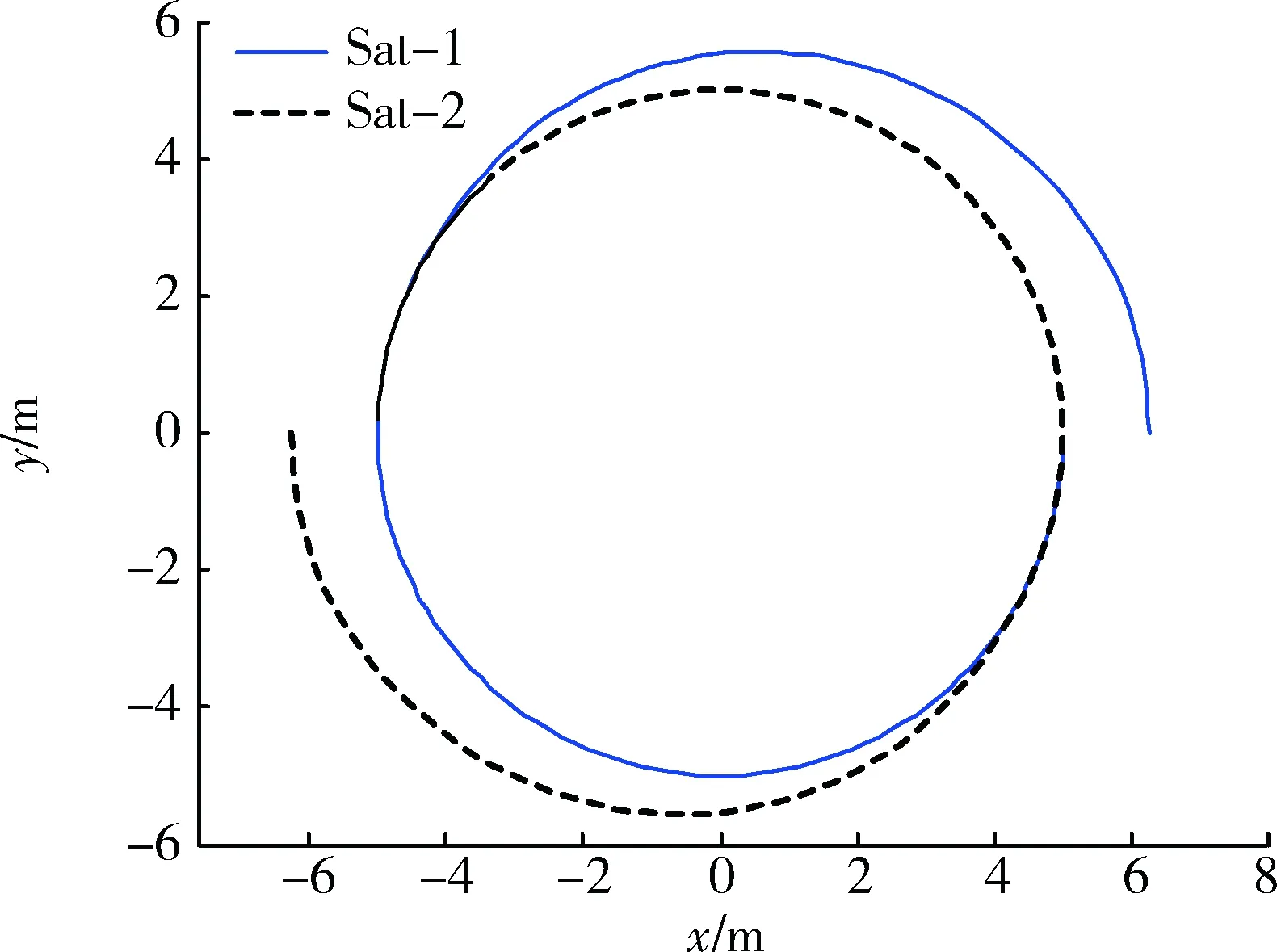
圖3 兩星在平動點L2處運行軌跡Fig.3 Trajectory of two satellites at libration point L2

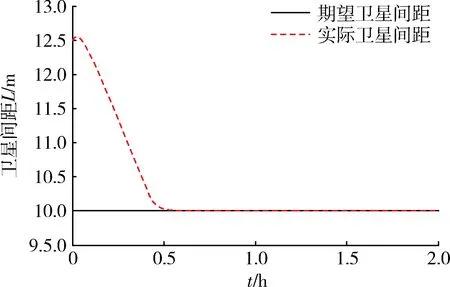
圖4 兩衛(wèi)星間隔距離隨時間變化曲線Fig.4 Satellite spacing distance change curve with time variation

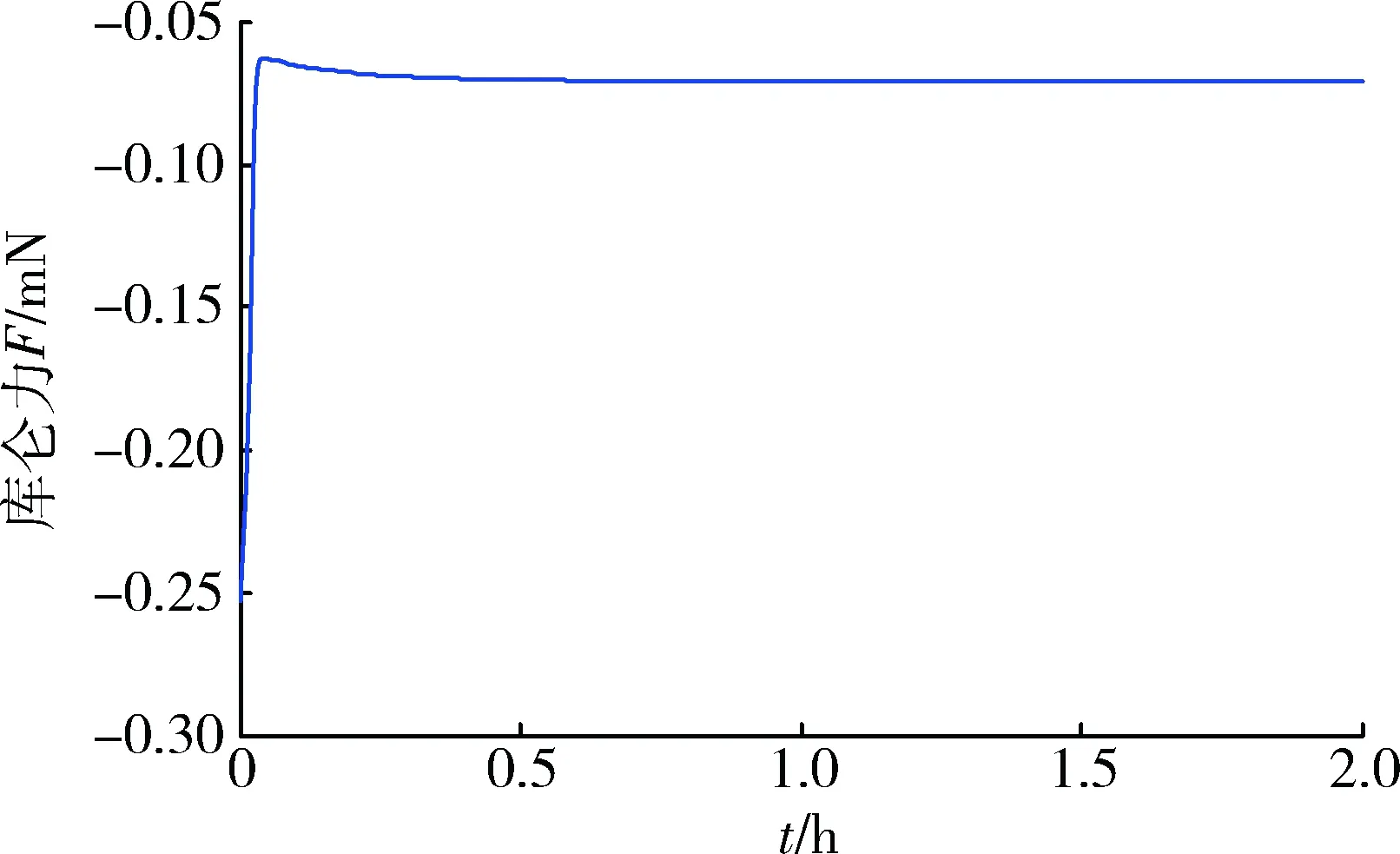
圖5 衛(wèi)星間庫侖力隨時間變化曲線Fig.5 Coulomb force curve with time variation

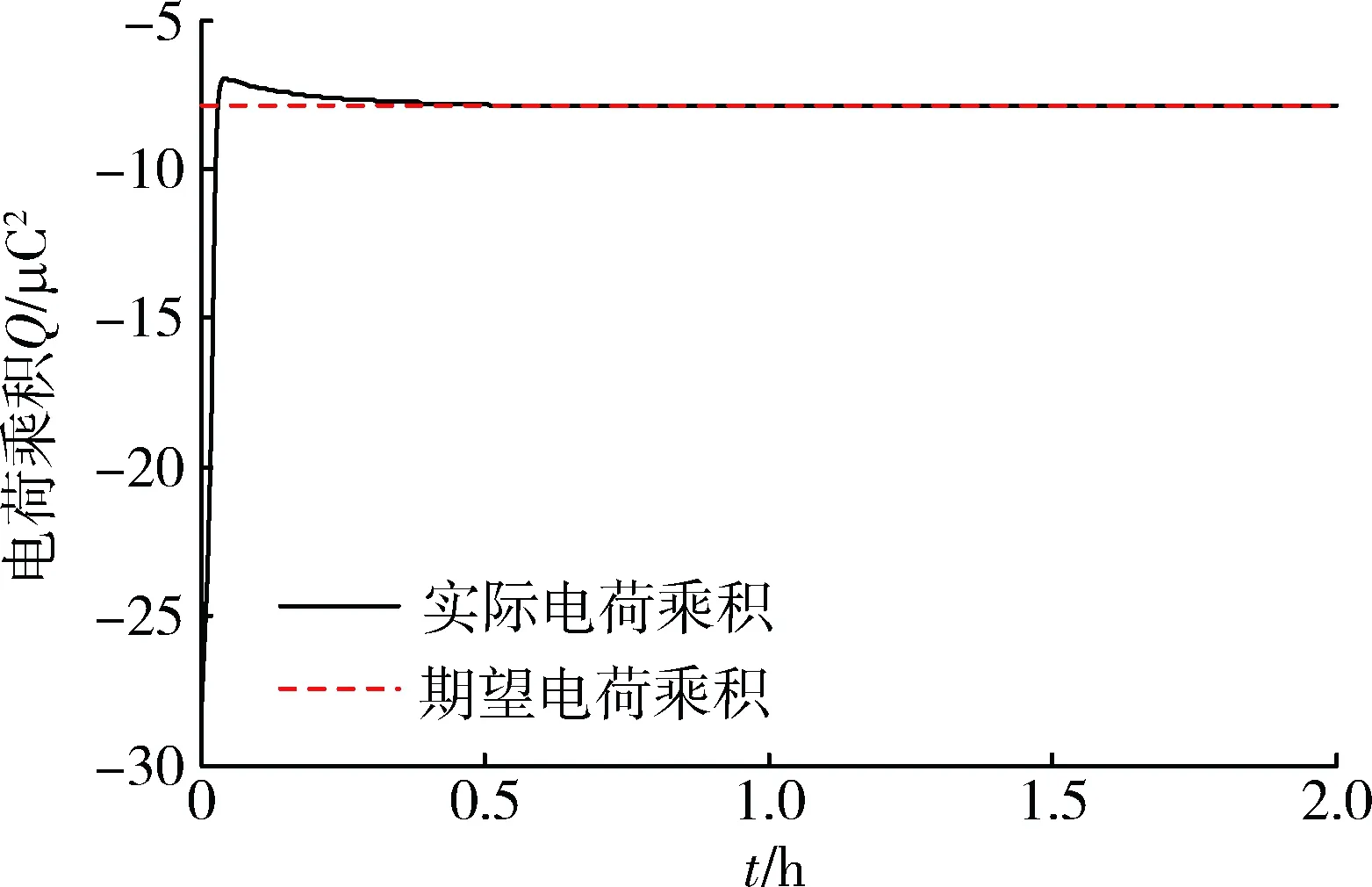
圖6 電荷乘積隨時間變化曲線Fig.6 Charge product change curve with time variation

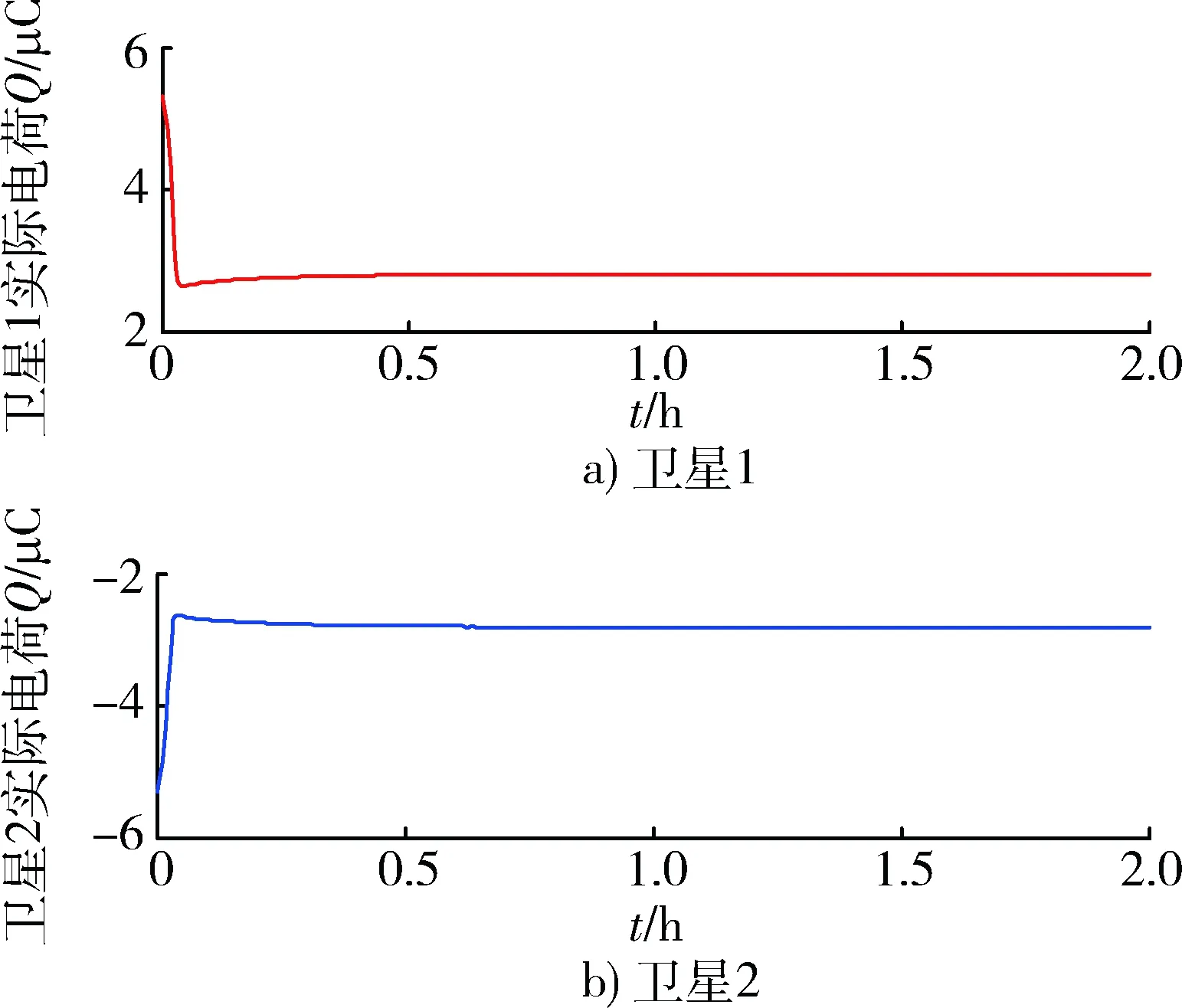
圖7 衛(wèi)星所帶電荷變化曲線Fig.7 Satellite charge change curve with time variation

圖3表示庫侖編隊系統(tǒng)在2 h內以地月系平動點L2點為質心的坐標系中的運動軌跡。由圖可以看出，兩顆衛(wèi)星通過改變所帶電量，從初始位置運動到間距不變的圓周運動。另外由圖4可知，在設計的線性化反饋滑模控制器的作用下，庫侖編隊系統(tǒng)能夠以較高的精度達到期望構型，在0.5 h左右，編隊達到期望間距并穩(wěn)定保持。說明本文在深空環(huán)境下，針對庫侖編隊特性所設計的線性化反饋滑模控制器能夠使編隊達到期望構型并保證系統(tǒng)的穩(wěn)定性，充分校驗了本文所提出的控制器的有效性，魯棒性和穩(wěn)定性。圖5表示兩顆衛(wèi)星之間庫侖作用力的大小，在兩衛(wèi)星運行初期衛(wèi)星所帶電荷和之間庫侖力變化比較大，隨著時間逐漸穩(wěn)定在定值-0.07 mN以消除外界環(huán)境以及重力勢能干擾。圖6，7分別表示衛(wèi)星所帶電荷乘積和單顆衛(wèi)星所帶電荷量大小，由于兩衛(wèi)星之間作用力為引力，所以兩顆衛(wèi)星電荷乘積為負值，所以兩衛(wèi)星帶異種電荷，大小相等，最后保持在2.81 μC左右。

4 結束語

本文針對于在深空環(huán)境中二體庫侖衛(wèi)星編隊控制問題，首先推導了在地月系L2點處二體庫侖衛(wèi)星編隊的動力學方程，根據動力學方程特點設計了線性化反饋滑模變結構控制器，滑模控制方法在控制過程中可以減少不確定因素的影響，并可以避免發(fā)生抖振現(xiàn)象，使二體庫侖衛(wèi)星編隊模型以較高的精確度達到期望構型。仿真驗證表明，設計的控制律有效，穩(wěn)定，具有良好的魯棒性。

[ 1] KING L B, PARKER G G， DESHMUKH S, et al. Spacecraft Formation Flying Using Inter-Vehicle Coulomb Force[R]. Tech. Rep. , NASA/NIAC, 2002.

[ 2] KING L B, PARKER G G, DESHMUKH S，et al. Study of Inter-Spacecraft Coulomb Forces and Implications for Formation Flying [J]. Journal of Propulsion and Power, 2003, 19(3):497-505.

[ 3] BERRYMAN J， SCHAUB H. Analytical Charge Analysis for Two-and Three-Craft Coulomb Formations [J]. Journal of Guidance, Control and Dynamics, 2007, 30(6):1701-1710.

[ 4] SCHAUB H, HALL C D, BERRYMAN J. Necessary Conditions for Circularly-Restricted Static Coulomb Formations [J]. Journal of the Astronautical Sciences, 2006, 54(3/4): 525-541.

[ 5] HUSSEIN I, SCHAUB H. Stability and Control of Relative Equilibria for the Three-Spacecraft Coulomb Tether Problem [J]. Journal of the Astronautical Sciences, 2008, 56(4):573-592.

[ 6] NATARAJAN A, SCHAUB H. Linear Dynamics and Stability Analysis of a Coulomb Tether Formation [J]. Journal of Guidance, Control and Dynamics, 2006, 29(4): 831-839.

[ 7] NATARAJAN A, SCHAUB H. Hybrid Control of Orbit Normal and Along-Track Two-Craft Coulomb Tethers [J]. Aerospace Science and Technology,2009,13(4):183-191.

[ 8] NATARAJAN A, SCHAUB H. Orbit-Nadir Aligned Coulomb Tether Reconfiguration Analysis[C]∥Spaceflight Mechanics Meeting, Galveston, TX, Jan 27-31, 2008.

[ 9] INAMPUDI R, SCHAUB H. Orbit Radial Dynamic Analysis of Two-Craft Coulomb Formation at Libration Points[C]∥ Astrodynamics Specialist Conference, Toronto, Canada, Aug 25, 2010.

[10] INAMPUDI R, SCHAUB H. Orbit-Radial Control of Two-Craft Coulomb Formation about Circular Orbits and Libration Points [C]∥The 4th International Conference on Spacecraft Formation Flying Missions and Technologies, May 18-20, 2011.

[11] WANG S, SCHAUB H. Nonlinear Coulomb Feedback Control of a Spinning Two Spacecraft Virtual Structure [C]∥American Control Conference, Minneapolis, USA, June 14-16, 2006.

[12] 王婷，張羽飛. 等質量立體五星庫侖編隊飛行的分析與控制[J].宇航學報，2015,36(11):1279-1288. WANG Ting, ZHANG Yu-fei，Analysis and Control for Three Dimensional Five-Satellite Coulomb Formation Flight in Geostationary Earth Orbit [J]. Journal of Astronautics，2015, 36(11):1279-1288.

[13] 張皓，師鵬，李保軍，等.利用庫侖力實現(xiàn)懸停軌道的新方法研究[J].宇航學報，2011, 33(1):68-75. ZHANG Hao, SHI Peng,LI Bao-jun, et al. Hover Orbit Using Inter-Spacecraft Coulomb Forces [J]. Journal of Astronautics，2011,33(1)：68-75.

[14] 黃靜,李傳江，馬廣富，等.考慮狀態(tài)約束的二體旋轉庫侖衛(wèi)星系統(tǒng)重構控制[J].宇航學報，2015,36(5):557-565. HUANG Jing, LI Chuan-jiang,MA Guang-fu, et al. Control for Reconfiguration of a Spinning Two-Body Coulomb Satellite System with State Constrains [J].Journal of Astronautics，2015,36(5):557-565.

[15] HUANG Jing, MA Guang-fu, LIU Gang. Nonlinear Dynamics and Reconfiguration Control of Two-Satellite Coulomb Tether Formation at Libration Points [J].Aerospace Science and Technology, 2014, 39(5): 501-512.

Feedback Linearization Sliding Mode Control of a Spinning Two-Body Coulomb Satellite Formation

WU Li-yao, YUAN Chang-qing, SHI Qiang

(Aviation University of Air Force, Aircraft and Power Department, Jilin Changchun 130022, China)

In order to reduce the uncertain factors of coulomb aircrafts formation movement process, avoid chattering of controlling process and increase the stability and veracity of controller, a feedback linearization sliding mode control method applied to the two-satellite formation flying at libration is designed. First the dynamics model two-satellite coulomb formation at earth-moon libration points are established and simplified, the feedback linearization is added with sliding mode control because of the characteristics of dynamics model to ensure robustness of formation. Simulation shows the method can make formation meet desired configuration with favorable control performance.

Coulomb satellite formation; libration points; feedback linearization; sliding mode control；simulation；robustness

2016-03-09；

2016-06-20 基金項目：國家自然科學基金(11372353) 作者簡介：吳立堯(1992-)，男，吉林遼源人。碩士生，主要從事庫侖航天器編隊動力學與控制。

10.3969/j.issn.1009-086x.2017.01.015

V448.2

A

1009-086X(2017)-01-0082-06

通信地址：130022 吉林省長春市東南湖大路2222號學員11隊