改進(jìn)PID的無人機(jī)飛行姿態(tài)角控制消顫算法*

陸興華, 詹世尉, 余文權(quán), 黃臣煒

(廣東工業(yè)大學(xué) 華立學(xué)院，廣東 廣州 511325)

計(jì)算與測試

改進(jìn)PID的無人機(jī)飛行姿態(tài)角控制消顫算法*

陸興華, 詹世尉, 余文權(quán), 黃臣煒

(廣東工業(yè)大學(xué) 華立學(xué)院，廣東 廣州 511325)

無人機(jī)在整個(gè)縱平面飛行過程中，由于飛行姿態(tài)角的大幅度變化以及氣流的作用，導(dǎo)致機(jī)身顫抖，影響飛行穩(wěn)定性。提出一種基于PID變結(jié)構(gòu)控制的無人機(jī)飛行姿態(tài)角控制消顫算法，首先進(jìn)行了無人機(jī)飛行姿態(tài)角控制系統(tǒng)的被控對象參量分析，構(gòu)建無人機(jī)在姿態(tài)角變化劇烈、大迎角飛行時(shí)的三通道模型，采用變結(jié)構(gòu)控制方法進(jìn)行控制器設(shè)計(jì)。結(jié)合小擾動原理和Lyapunov穩(wěn)定性原理進(jìn)行擾動抑制和穩(wěn)定性證明，采用梯度算法調(diào)整權(quán)值進(jìn)行飛行姿態(tài)角控制的消顫處理，采用自適應(yīng)算法在線調(diào)整權(quán)值實(shí)現(xiàn)PID變結(jié)構(gòu)控制改進(jìn)。仿真結(jié)果表明：采用該算法進(jìn)行無人機(jī)飛行姿態(tài)角控制和消顫處理，大幅度提高無人機(jī)飛行定姿的精度，橫滾角、俯仰角和航向角的控制精度有較大提高，穩(wěn)定性和收斂性較好，確保了無人機(jī)飛行穩(wěn)定性。

無人機(jī)； 神經(jīng)網(wǎng)絡(luò)； 變結(jié)構(gòu)控制； 姿態(tài)角

0 引 言

無人機(jī)(unmanned aerial vehicle,UAV)的穩(wěn)定性飛行控制一直是制約無人機(jī)發(fā)展的一個(gè)重要瓶頸技術(shù)，無人機(jī)的氣動特性具有靜不穩(wěn)定性，在整個(gè)縱向平面飛行過程中，受到大氣密度和空氣流動等飛行條件的不斷變化的影響，導(dǎo)致無人機(jī)不能穩(wěn)定飛行，引起機(jī)身顫抖和擾動，較小的機(jī)身顫抖和擾動都會引起無人機(jī)的橫滾和姿態(tài)偏移，甚至導(dǎo)致飛行穩(wěn)定性失衡，引起墜機(jī)事故。因此，研究無人機(jī)的飛行姿態(tài)角控制和消顫方法，在保障無人機(jī)飛行穩(wěn)定中具有重要的意義[1]。

在無人機(jī)的飛行姿態(tài)角控制系統(tǒng)設(shè)計(jì)中，最關(guān)鍵的技術(shù)是構(gòu)建無人機(jī)動力平衡數(shù)學(xué)控制模型[2,3]。采用變結(jié)構(gòu)自適應(yīng)理論在姿態(tài)控制系統(tǒng)設(shè)計(jì)中的具有一定的可行性，對此，文獻(xiàn)[4]提出一種基于不確定邊界的自適應(yīng)神經(jīng)網(wǎng)絡(luò)控制的飛行器的姿態(tài)角慣導(dǎo)控制方法，進(jìn)行了采用簡化模型的變結(jié)構(gòu)自適應(yīng)控制器設(shè)計(jì)，提高了飛行器的控制精度，但是該方法在飛行器進(jìn)行大幅度縱向提升過程中的控制性能不好，誤差較大[5]。PID神經(jīng)網(wǎng)絡(luò)控制算法將靜態(tài)神經(jīng)元擴(kuò)充到動態(tài)神經(jīng)元，在無人機(jī)飛行控制中具有結(jié)構(gòu)簡單，實(shí)時(shí)性好等優(yōu)點(diǎn)[6]。

本文在傳統(tǒng)的PID控制方法的基礎(chǔ)上，針對傳統(tǒng)方法無法使被控對象得到有效的干擾抑制和顫抖補(bǔ)償?shù)膯栴}，進(jìn)行了控制算法改進(jìn)設(shè)計(jì)，提出一種基于PID變結(jié)構(gòu)控制的無人機(jī)飛行姿態(tài)角控制消顫算法，仿真實(shí)驗(yàn)驗(yàn)證，方法具有很好的適應(yīng)性，而且可以保證很高的控制精度。

1 無人機(jī)飛行姿態(tài)控制對象描述和參量分析

1.1 被控對象描述

無人機(jī)姿態(tài)控制具有運(yùn)動參數(shù)的時(shí)變性、參數(shù)及擾動的隨機(jī)變化性、控制對象及設(shè)備的嚴(yán)重非線性以及彈性振動等特性，上述飛行姿態(tài)特點(diǎn)可能導(dǎo)致無人機(jī)在飛行過程中出現(xiàn)顫抖和大幅度擾動，對飛行安全帶來隱患。對此，需要進(jìn)行無人機(jī)的飛行姿態(tài)控制，在無人機(jī)飛行姿態(tài)角控制過程中，整個(gè)飛行段選取不同的特征點(diǎn)并得到相應(yīng)點(diǎn)的線性時(shí)不變對象模型，構(gòu)建確定性模型描述無人機(jī)飛行的被控對象，進(jìn)行控制對象的參量構(gòu)建和描述，無人機(jī)飛行姿態(tài)角的控制參量主要包括了確定性參量和不確定性參量兩大部分[7～10]。不確定量主要包括參數(shù)的不確定性和外界的擾動，根據(jù)上述分析，構(gòu)建無人機(jī)在姿態(tài)角變化劇烈、大迎角飛行時(shí)的三通道模型表述為

(1)

(2)

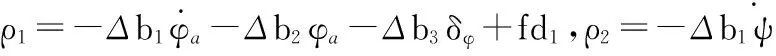
(3)

(4)

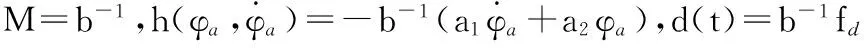
(5)

在上述被控對象參量分析的基礎(chǔ)上，進(jìn)行無人機(jī)飛行姿態(tài)角控制的運(yùn)動分析和控制器設(shè)計(jì)。

1.2 無人機(jī)飛行姿態(tài)角控制的定常運(yùn)動分析

通過對無人機(jī)飛行姿態(tài)角控制的定常運(yùn)動分析，進(jìn)行控制器優(yōu)化設(shè)計(jì)，無人機(jī)飛行控制是一個(gè)封閉的控制系統(tǒng)，由縱向定常運(yùn)動分析，構(gòu)建無人機(jī)的縱向運(yùn)動方程。

M=Mn+ΔM

(6)

(7)

(8)

其中

(9)

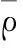
(10)

在上界已知的情況下，進(jìn)行飛行姿態(tài)角的控制器設(shè)計(jì)。

2 控制器設(shè)計(jì)和消顫算法改進(jìn)設(shè)計(jì)

2.1 上界已知時(shí)無人機(jī)飛行姿態(tài)角控制變結(jié)構(gòu)控制器

無人機(jī)飛行控制系統(tǒng)是一個(gè)多變量、非線性、強(qiáng)耦合系統(tǒng)，采用變結(jié)構(gòu)方法設(shè)計(jì)的姿態(tài)控制系統(tǒng)比采用經(jīng)典理論設(shè)計(jì)的姿態(tài)控制系統(tǒng)具有更強(qiáng)的魯棒性和較高的精確度，對此，采用變結(jié)構(gòu)控制方法進(jìn)行控制器設(shè)計(jì)，在縱向定常運(yùn)動上界已知的情況下，令

(11)

當(dāng)不考慮無人機(jī)飛行姿態(tài)角控制系統(tǒng)的不確定因素時(shí)，得到所有魯棒PID控制器參數(shù)集，得到俯仰角跟蹤控制的誤差向量形式為

(12)

通過上述方程聯(lián)立，求得無人機(jī)飛行控制的角速度的跟蹤誤差，此時(shí)將幾何控制域中的滑模面定義為

s=ce1+e2

(13)

則

(14)

令

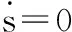
(15)

考慮系統(tǒng)存在不確定因素，在實(shí)際的無人機(jī)飛行彈道中，計(jì)算縱向運(yùn)動參數(shù)和橫舵角的非線性函數(shù)，得到姿態(tài)平衡到達(dá)律為

(16)

則總的量為

u=ueq+u0

(17)

根據(jù)上述描述，實(shí)現(xiàn)無人機(jī)飛行姿態(tài)角控制器設(shè)計(jì)。

2.2 基于變結(jié)構(gòu)PID的消顫算法改進(jìn)

在上述進(jìn)行控制器設(shè)計(jì)的基礎(chǔ)上，采用一種基于PID變結(jié)構(gòu)控制的無人機(jī)飛行姿態(tài)角控制消顫算法實(shí)現(xiàn)對干擾抑制和無人機(jī)的機(jī)身顫抖補(bǔ)償，本文設(shè)計(jì)的變結(jié)構(gòu)PID神經(jīng)網(wǎng)絡(luò)控制器采用的是三層前向神經(jīng)元網(wǎng)絡(luò)，為2×3×1結(jié)構(gòu)，結(jié)合上述的控制器設(shè)計(jì)，采用梯度算法調(diào)整權(quán)值進(jìn)行機(jī)身消顫處理，無人機(jī)在受到擾動下的定常俯仰跟蹤角度在PID神經(jīng)網(wǎng)絡(luò)的輸出為

(18)

此時(shí)，變結(jié)構(gòu)PID神經(jīng)元的狀態(tài)uj由線性方程組的擾動參量決定。在神經(jīng)網(wǎng)絡(luò)中采用自變量進(jìn)行自適應(yīng)學(xué)習(xí)，按其狀態(tài)函數(shù)可得控制參量的基礎(chǔ)輸出，即

uj(k+1)=g(netj-θj,uj(k))

(19)

式中 θj為神經(jīng)元的誤差曲面，本文在無人機(jī)飛行控制中均設(shè)閾值為零。神經(jīng)網(wǎng)絡(luò)控制系統(tǒng)的輸出層神經(jīng)元的輸出函數(shù)與線性化的小擾動特征輸出相同，輸出為

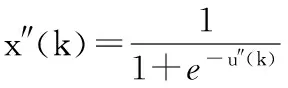
(20)

根據(jù)小擾動原理，得到無人機(jī)飛行中的PID神經(jīng)網(wǎng)絡(luò)的輸出v(k)與基準(zhǔn)運(yùn)動狀態(tài)有關(guān)，即

v(k)=x″(k)

(21)

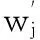
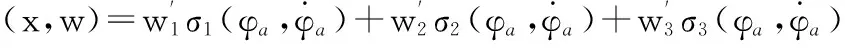
(22)

(23)

式中 ∫(·)dt為多變量控制系統(tǒng)的積分器，在無人機(jī)飛行姿態(tài)角控制中為一個(gè)與推力矩相平衡的限幅參量，而d(·)是微分符號。通過上述分析得知，本文設(shè)計(jì)的改進(jìn)的PID變結(jié)構(gòu)自適應(yīng)學(xué)習(xí)無人機(jī)飛行姿態(tài)角控制系統(tǒng)是穩(wěn)定的，系統(tǒng)的穩(wěn)定性得證。

3 仿真分析

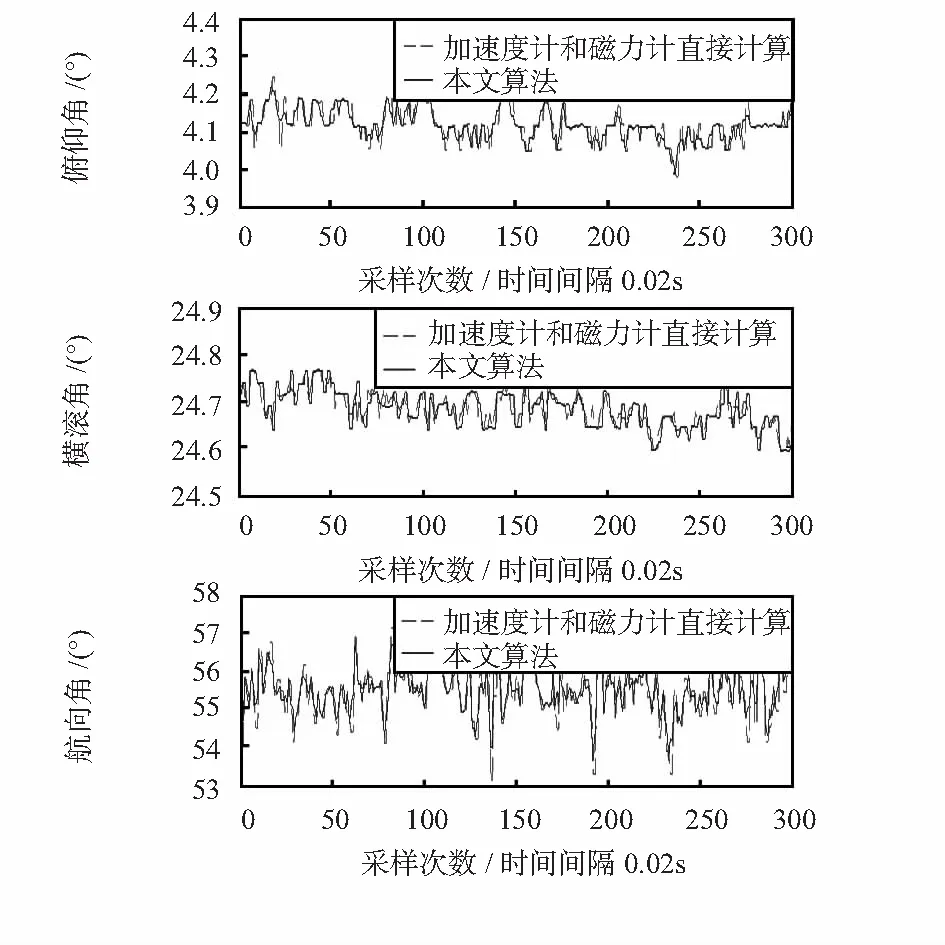
圖1 無人機(jī)飛行姿態(tài)角比較

從圖1可見，采用本文方法進(jìn)行無人機(jī)飛行姿態(tài)控制，姿態(tài)角控制效果的非常平滑，有效避免了擾動干擾，零點(diǎn)漂移幾乎為零，控制系統(tǒng)的穩(wěn)定性較好，效果比傳統(tǒng)的計(jì)算方法提高了定姿的精度。分析仿真結(jié)果得出，采用本文設(shè)計(jì)的控制器能夠在很短的時(shí)間內(nèi)將無人機(jī)的姿態(tài)角誤差調(diào)整到零，對參數(shù)變化及隨機(jī)干擾具有很好的適應(yīng)性，通過本文的消顫處理，有效提高了飛行姿態(tài)角的穩(wěn)定性，擾動干擾得到有效控制。而采用傳統(tǒng)控制方法由于沒有進(jìn)行消顫處理，導(dǎo)致姿態(tài)角輸出不穩(wěn)定。在相同實(shí)驗(yàn)參數(shù)下，采用不同算法得到無人機(jī)飛行控制的姿態(tài)角最大誤差、平均誤差和均方差結(jié)果見表1。分析表中結(jié)果可見，采用本文控制方法，能大幅度提高無人機(jī)飛行定姿的精度，橫滾角較傳統(tǒng)的兩種方法分別提高了60 %，42 %，俯仰角提高了46 %，27 %，航向角精度提高64 %，50 %，在無人機(jī)飛行姿態(tài)穩(wěn)定性控制中具有較好優(yōu)勢。

表1 不同算法姿態(tài)控制誤差結(jié)果統(tǒng)計(jì)

4 結(jié)束語

本文以無人機(jī)三通道姿態(tài)運(yùn)動的動力學(xué)模型為被控對象，在不確定上界已知的情況下，進(jìn)行了無人機(jī)飛行姿態(tài)角的變結(jié)構(gòu)PID改進(jìn)控制器設(shè)計(jì)，通過Lyapunov穩(wěn)定性理論進(jìn)行了控制器的穩(wěn)定性證明。采用自適應(yīng)算法在線調(diào)整權(quán)值實(shí)現(xiàn)對無人機(jī)的消顫控制和小擾動抑制處理，研究結(jié)果表明:采用本文方法進(jìn)行無人機(jī)飛行姿態(tài)角控制和消顫設(shè)計(jì)，能夠在很短的時(shí)間內(nèi)將無人機(jī)的姿態(tài)角誤差調(diào)整到零，大幅度提高無人機(jī)飛行定姿的精度，有效保證了飛行穩(wěn)定性。

[1] Feyzmahdavian H R,Charalambous T,Johansson M.Exponential stability of homogeneous positive systems of degree one with time-varying delays[J].IEEE Transactions on Automatic Control,2014,59(6):1594-1599.

[2] Zhang J F,Han Z Z,Wu H.Robust finite-time stability and stabilization of switched positive systems[J].IET Control Theory and Applications,2014,8(1):67-75.

[3] Ngoc P H A.Stability of positive differential systems with dela-y[J].IEEE Transactions on Automatic Control,2013,58(1):203-209.

[4] Xiang M,Xiang Z R,Karimi H R.Stabilization of positive switched systems with time-varying delays under asynchronous swit-ching[J].International Journal of Control,Automation and Systems,2014,12(5):939-947.

[5] 章 俊,張冬梅,王辛剛.一類參數(shù)不確定連續(xù)正系統(tǒng)受限控制[J].信息與控制,2015,44(5):592-597,603.

[6] 朱 熠， 陳 欣， 李春濤，等.風(fēng)擾動下的飛翼無人機(jī)靜態(tài)投影控制[J].兵工學(xué)報(bào),2015,36(7):1237-1246.

[7] 雷旭升,陶 冶.小型無人飛行器風(fēng)場擾動自適應(yīng)控制方法[J].航空學(xué)報(bào),2010,31(6):1171-1176.

[8] 張明廉.飛行控制系統(tǒng)[M].北京:北京航空航天大學(xué)出版社,2006.

[9] 劉 重， 高曉光， 符小衛(wèi)，等.基于反步法和非線性動態(tài)逆的無人機(jī)三維航路跟蹤制導(dǎo)控制[J].兵工學(xué)報(bào),2014,35(12):2030-2040.

[10] 呂 品，賴際舟，劉建業(yè)，等.飛行器氣動模型輔助導(dǎo)航方法的研究概況與進(jìn)展[J].控制與決策,2015,30(12):2113-2120.

[11] 楊天雨,賈文峰,賴際舟,等.慣性/光流/磁組合導(dǎo)航技術(shù)在四旋翼飛行器中的應(yīng)用[J].傳感器與微系統(tǒng),2016,35(1):156-160.

Flight attitude angle control and anti-chatter algorithm for UAV based on improved PID*

LU Xing-hua, ZHAN Shi-wei, YU Wen-quan, HUANG Chen-wei

(Huali College,Guangdong University of Technology，Guangzhou 511325， China)

Aiming at problem that UAV in the whole longitudinal plane flight process,due to the large range of flight attitude angle and the effect of air flow,resulting in trembling,affecting flight stability,present a control and anti-chatter algorithm for UAV flight attitude angle based on PID variable structure control.Parametric analysis on controlled object of flight attitude angle control system is carried out. Three-channel model for UAV in dramatic change of attitude angle, large angle of attack flight,controller is designed with variable structure control method.The disturbance rejection and stability are proved by small perturbation theory and Lyapunov stability theory.Gradient algorithm is used to adjust weights for anti-chatter processing by flight attitude angle control.The adaptive algorithm is used to online adjust the weights to realize improvement of PID variable structure control.The simulation results show that using this algorithm to control attitude angle of UAV and realize anti-chatter,precision of UAV flight attitude is greatly improved,the control precision of roll angle,pitch angle and heading angle is greatly improved,stability and convergence are good, which ensure flight stability of UAV.

unmanned aerial vehicle(UAV); neural network; variable structure control; attitude angle

10.13873/J.1000—9787(2017)03—0116—04

2016—03—31

2015年廣東省教育廳重點(diǎn)平臺及科研項(xiàng)目青年創(chuàng)新人才類項(xiàng)目(自然科學(xué)類)(2015KQNCX218)； 2016年廣東省大學(xué)生科技創(chuàng)新培育項(xiàng)目(pdjh2016b0940)

TP 273

A

1000—9787(2017)03—0116—04

陸興華(1981-)，男，碩士，講師，主要從事計(jì)算機(jī)控制算法、人工智能等研究工作。