空間快速交會停泊軌道優化設計

魏鵬濤

(火箭軍指揮學院，湖北 武漢 430012)

空間快速交會停泊軌道優化設計

魏鵬濤

(火箭軍指揮學院，湖北 武漢 430012)

針對空間快速交會問題，采用一種新的停泊軌道轉移交會的方式。對該停泊軌道優化問題進行了數學描述，建立了停泊軌道優化模型，采用遺傳算法進行了仿真計算。結果表明，所設計停泊軌道能滿足空間快速交會要求。

空間軌道；快速交會；停泊軌道；優化設計；數學模型；遺傳算法

0 引言

隨著太空作用的日益凸顯，空間飛行器逐漸增多，其在國防、經濟等各個方面發揮著越來越重要的作用，未來將面臨實現航天器與空間飛行器的快速交會任務。目前，對于空間快速交會，研究較多的是地面發射航天器快速進入目標軌道，對目標飛行器實施交會的方式。此外，部分文獻研究了先將航天器發射到比目標軌道高度較高或較低的軌道，然后根據指令進行軌道轉移實施交會的方式[1-9]。這些方式交會時間較長，能量需求較多。為了縮短交會時間，減小能量消耗，本文提出了將航天器發射到與目標軌道有交會點的軌道先期運行，根據指令在該交會點進行快速轉移，對目標實施交會的方式，并對該軌道進行了優化設計，可為空間快速交會提供參考。

1 問題描述

為了實現空間快速交會，可將航天器先運行于某一與空間目標不碰撞的軌道，稱之為停泊軌道[1]。當接收到轉移指令后，航天器實施軌道轉移，進入交會軌道，完成交會任務。為了縮短交會時間，減少能量需求，可考慮設計停泊軌道與目標軌道有軌道交會點，航天器在該軌道交會點進行軌道轉移實施快速交會的方式。該方式具體表述為：航天器首先由火箭發射到停泊軌道，當接到軌道轉移指令時，在該軌道交會點進行軌道轉移進入交會軌道，使航天器落后空間目標某一飛行時間，隨后航天器捕獲目標，通過末制導軌道機動進行交會，該交會方式工作流程如圖1所示。

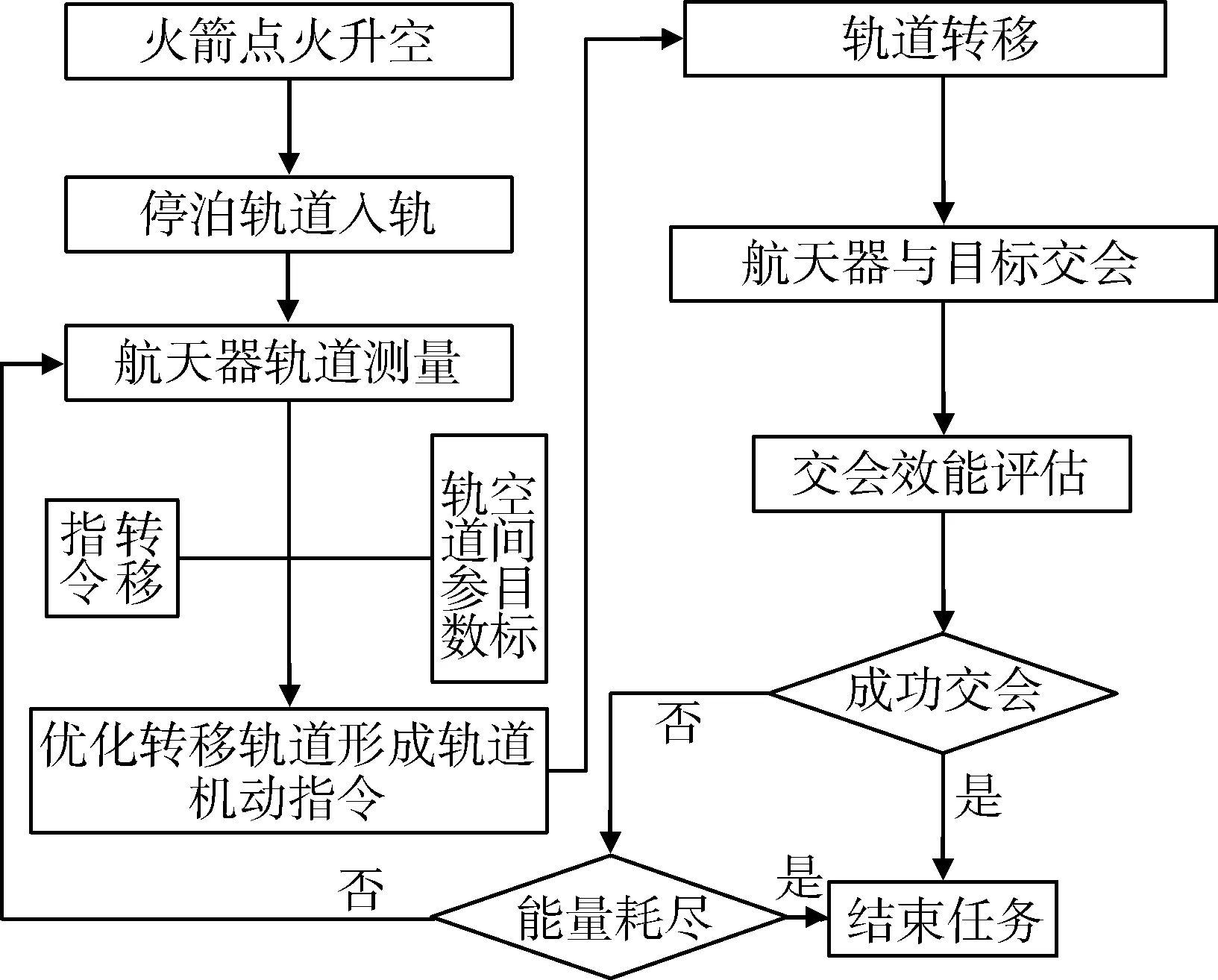
圖1 航天器交會流程圖Fig.1 Flowchart of spacecraft rendezvous

航天器交會軌道要與目標軌道相同，其停泊軌道滿足條件如下。

(1) 停泊軌道向交會軌道轉移點的定軌精度要高，即轉移點位置確定。

(2) 航天器在停泊軌道運行時不能與空間目標碰撞，為保證在任意一次到達停泊軌道和交會軌道的交點時均可實施沖量軌道轉移，要求到達軌道轉移點時刻航天器和空間目標的相對位置不變，因此，停泊軌道的運行周期應該與空間目標軌道的運行周期一致，即TT=TM=T。

(3) 航天器進入交會軌道，落后空間目標時間為ΔT。

(4) 停泊軌道向交會軌道轉移能量消耗小，即所需速度沖量小，因而選用一次沖量方案。

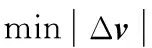
2 停泊軌道優化模型[10-13]

空間目標軌道周期表達式為

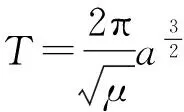
(1)

從式(1)可以看出，空間目標運行周期只與半長軸有關，由第1節結論(3)可知，目標軌道和停泊軌道周期相等，故

aT=aM.

(2)

設停泊軌道到交會軌道轉移點為R，該點在停泊軌道上的真近點角為fT，由橢圓彈道方程得轉移點地心距rT為

(3)

由于轉移點地心距rT為已知量，由式(2)，(3)可知，eT可以表示為fT的函數。

設停泊軌道在軌道轉移點R的速度矢量為vT，其與轉移點R地心矢徑之間的夾角為θT，交會軌道在軌道轉移點R的速度矢量為vJ，其與轉移點R地心矢徑之間的夾角為θJ，因此航天器由停泊軌道轉移到交會軌道所需速度沖量為

Δv=vJ-vT.

(4)

為了計算Δv，建立如下交點坐標系[B]，以交點R的地心矢徑為Oy軸，在停泊軌道面內垂直于Oy軸的方向為Ox軸，其指向運動方向，Oz軸、Ox軸和Oy軸構成右手直角坐標系，如圖2所示。

圖2 軌道轉移點坐標Fig.2 Coordinate of orbit transfer point

圖2中，φ為停泊軌道平面和交會軌道平面之間的夾角，φ=iT-iJ。vT和vJ在交點坐標系中可表示為

(5)

式中：vT為vT的大小；vJ為vJ的大小。

由橢圓軌道理論，可得停泊軌道在軌道轉移點R的徑向速度大小vTr和周向速度大小vTf以及總速度大小vT分別表示為

(6)

由圖1可知，θT可表示為

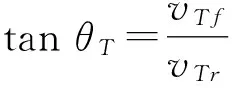
(7)

同理可求出θJ，因此可得到Δv和φ與fT的關系式。

假設空間目標通過其軌道近地點為0時刻，通過K點的時刻為tK；航天器通過軌道轉移點R的時刻為tR，通過交會軌道近地點時刻為t0。航天器進入交會軌道經過時間ΔT到達K點，因而可得tK=tR+ΔT。在時刻tK，空間目標的真近點角fMK和航天器的真近點角fLK分別如圖3所示。

圖3 空間目標和航天器在交會軌道示意圖Fig.3 Diagrammatic sketch of rendezvous orbit about space target and spacecraft

圖3中，vL為航天器在交會軌道近地點處的速度大小；vM為空間目標在其軌道上近地點處的速度大小；P為目標軌道近地點；fR為航天器交會軌道R點的真近點角。

對于交會軌道，有下列關系式

(8)

式中:ER為交會軌道R點處的偏近點角;EK為交會軌道K點處的偏近點角；TJ為交會軌道周期。tR，t0，ER，EK，fLK為未知量，解上述方程組可以求得fLK。

由圖3可知

fLK=fMK.

(9)

對于目標軌道，有

(10)

式中:EM為目標軌道K點處的偏近點角；TM為目標軌道周期。

由式(9)，(10)可得到tK，因而可得到tR及t0。

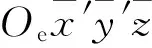
由橢圓軌道理論可以得到t時刻空間目標的位置關系式

(11)

式中：EMt，fMt和rMt分別為在t時刻目標軌道位置的偏近點角、真近點角和地心距。

解算式(11)，則可得到t時刻目標軌道點的真近點角fMt和地心距rMt。因而，可得到t時刻空間目標在近焦點坐標系的坐標

rMt=(rMtcosfMt,rMtsinfMt,0)，

(12)

式中：rMt空間目標t時刻地心矢徑向量。

(13)

式中：TT為停泊軌道周期；ETR為航天器在停泊軌道tR時刻的偏近點角。

同理，t時刻航天器在停泊軌道的位置關系式為

(14)

式中：ETt為和fTt分別為航天器在停泊軌道t時刻的偏近點角和真近點角。

因而，可得到t時刻航天器在停泊軌道近焦點坐標系的坐標為

rTt=(rTtcosfTt,rTtsinfTt,0)，

(15)

式中：rTt為航天器在停泊軌道t時刻地心矢徑向量。

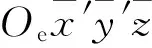
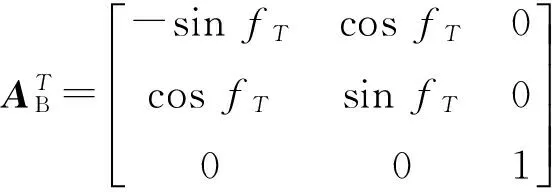
(16)

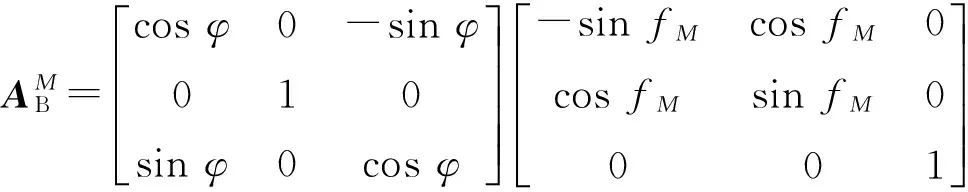
(17)

于是，t時刻航天器和空間目標之間的距離d滿足下列條件

(18)

(1) 優化目標

(2) 約束條件

min{d(t)}>D.

(3) 優化量

X=(φ,fT).

求得這2個最優量后，就可以求出其他停泊軌道參數。

3 遺傳算法仿真計算

本文選用遺傳算法[14-16]作為停泊軌道優化算法。對于目標函數中的目標變量要服從一定約束條件的優化問題，最常用的方法是采用懲罰函數的方法，將有約束的極值問題變為無約束的極值問題。

(1) 編碼

對于本問題，目標變量的有效數字很多，采用二進制編碼的字符串長度很大，使得復制、變換、突變等操作占用計算機時間很長，相比之下，如用十進制編碼，不僅無需轉化數制便于理解，而且節省遺傳操作的時間，因此采用十進制編碼。

(2) 初始群體產生

采用隨機生成的方法建立初始群體。當遺傳的群體規模取到適當個體數目時，利用這種隨機方法產生的群體既可以比較均勻地散布到整個的搜索空間，又不致使群體形態過于分散，導致收斂困難。

(3) 適應度的計算

本文求解的是最小值問題，因此適應度函數值越小，其適應度越高。所以適應度函數取為

(19)

式中:Fit為適應度函數值；N為懲罰數；D為安全距離。

(4) 選擇操作

本文采用錦標賽選擇。首先隨機地在群體中選擇2個個體進行比較，適應度最好的個體將被選擇作為生成下一代的父代個體。這種選擇方式也使得適應度好的個體具有較大的“生存”機會。同時，由于它只使用適應度的相對值作為選擇的標準，而與適應度的數值大小不成直接比例，所以它也能避免超級個體的影響，在一定程度上，防止過早收斂和停滯現象的發生。

(5) 交叉操作

在連續型遺傳算法中，每個十進制數被視作一個基因整體，所以采用算術交叉法來進行交換計算，對于父代個體a和b，交叉操作產生2個新個體a′和b′為

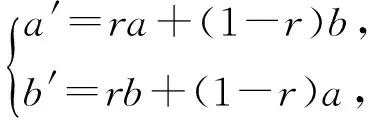
(20)

式中：r為[0,1]之間的隨機數。

(6) 服務變異操作

變異操作采用非均勻變異方法，個體基因參數為c，則變異產生的新個體基因c′為

(21)

式中：cmax為基因的最大值；cmin為基因的最小值；G為最大允許迭代次數；g為當前迭代次數；r為[0,1]之間的隨機數。

(7) 算法步驟

1) 建立初始群體；

2) 計算個體的適應度；

3) 根據遺傳概率,依次進行選擇，交叉和變異操作產生新個體；

4) 反復執行2)和3)，直至達到終止條件,選擇最佳個體作為遺傳算法的結果。

利用前面設計的算法和模型，對停泊軌道進行優化計算。

假設空間目標軌道參數如表1所示，軌道轉移點在目標軌道上位置為fM=329.257°，ΔT=600 s，安全距離取30 km。停泊軌道平面和交會軌道平面的夾角φ的取值范圍為[0,1°]，交點在停泊軌道真

近點角取值范圍為[0,360°)。

大量計算表明，群體規模取100，交叉概率取0.9，變異概率取0.15，終止代數取200，代溝取0.8，得到結果較好，迭代結果如圖4所示。優化結果為fT=325.193 7°，φ=0.080 2°，Δv=30.851 1 m/s。因此，航天器停泊軌道的其他參數如表2所示。

通過上面仿真可以看出，通過合理設計停泊軌道，使航天器進入交會軌道時與空間目標的相對距離滿足末制導距離要求，航天器探測裝置捕獲空間目標后就可實現快速交會。

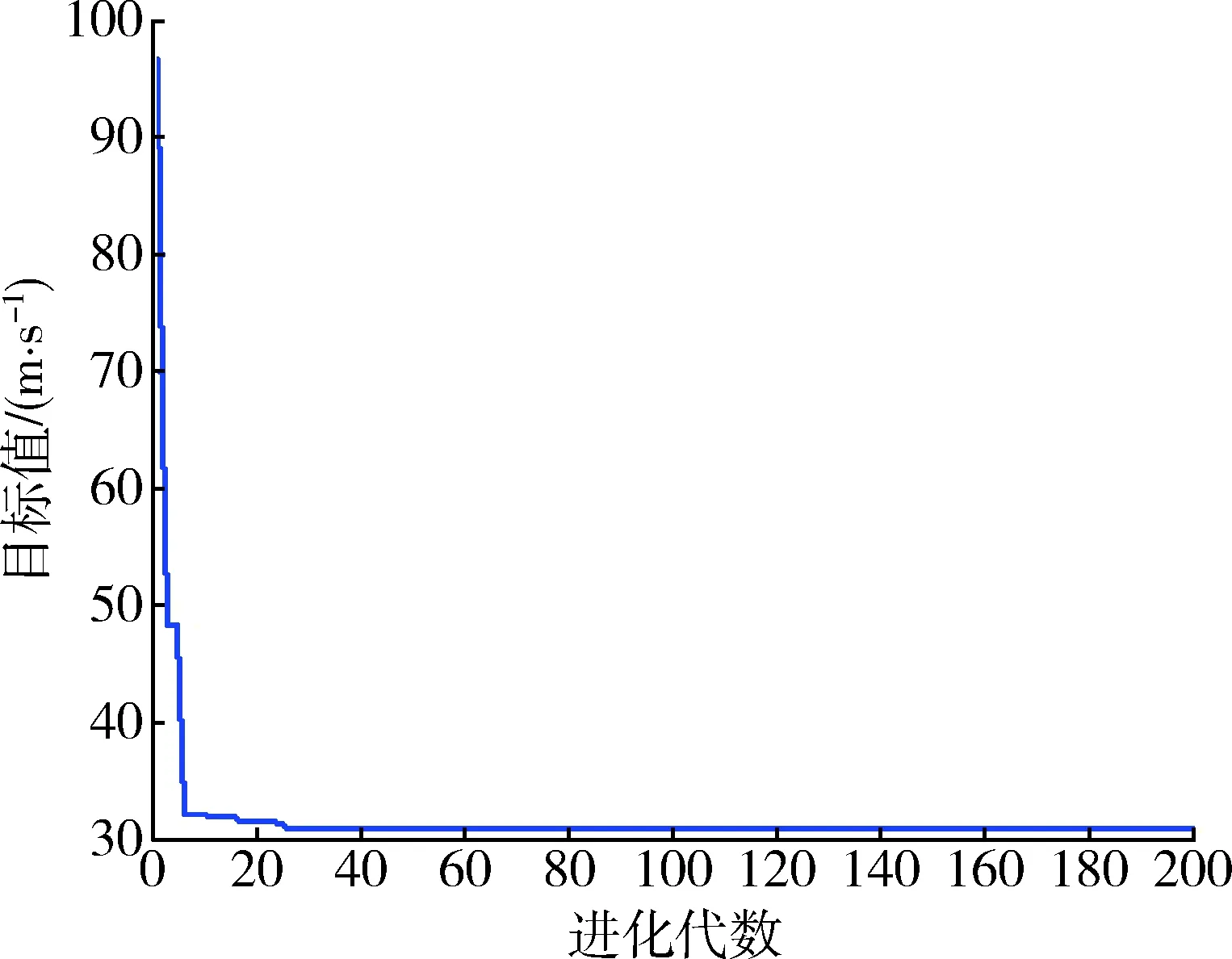
圖4 優化結果與進化代數曲線圖Fig.4 Graphs of optimal result and evolutional generation

表1 空間目標軌道參數

Table 1 Orbital elements of space target

參數名長半軸/km偏心率軌道傾角/(°)升交點赤經/(°)近地點幅角/(°)數值7017.19070.045797.8000300.000090.0000

表2 停泊軌道參數

4 結束語

空間快速交會具有多種方式，各種方式具有不同的特點。本文以縮短交會時間，減小能量消耗為目標，采用了在交會點進行轉移的交會方式，建立了停泊軌道的優化模型，并以某空間目標為對象進行了仿真計算，結果表明該交會方式具有可行性。本文成果可為空間快速交會實際應用提供理論借鑒和參考。

[ 1] 吳蓓蓓，黃海．空間多目標攔截交會平臺停泊軌道設計優化[J]．航天控制，2012，30(4)：54-59． WU Bei-bei，HUANG Hai．The Design and Optimization of the Parking Orbit of Space Multiple-Targets Rendezvous or Interception Platform [J]．Aerospace Control，2012，30(4)：54-59．

[ 2] 魏鵬濤，雷剛，郭洪娜，等．基于Lambert轉移的虛交點軌道攔截優化[J]．飛行力學，2012，30(6)：556-559． WEI Peng-tao，LEI Gang，GUO Hong-na，et al．Orbit Interception at Virtual Crossing Point Based on Lambert Transfer [J]．Flight Dynamics，2012，30(6)：556-559．

[ 3] 閆循良．基于空間發射的組合機動路徑規劃研究[D]．西安：西北工業大學，2011． YAN Xun-liang．Study on the Combined Maneuver Path Planning Based on Space Launch [D]．Xi’an：Northwestern Polytechnical University，2011．

[ 4] 錢宇．在軌航天器空間規避研究[D]．西安：西北工業大學，2011． QIAN Yu．Study on Space Avoidance of Orbit Spacecraft[D]．Xi’an：Northwestern Polytechnical University，2011．

[ 5] 馬丹山，王明海，鮮勇，等．逆軌道攔截衛星軌道設計與優化[J]．飛行力學，2009，27(5)：63-65． MA Dan-shan，WANG Ming-hai，XIAN Yong，et al．Orbit Design and Optimization of Reverse Orbit Interception Satellite [J]．Flight Dynamics，2009，27(5)：63-65．

[ 6] 齊映紅．小衛星追蹤攔截制導問題研究[D]．哈爾濱：哈爾濱工業大學，2009． QI Ying-hong．Research on Interception Guidance of Small Satellite Tracking [D]．Harbin：Harbin Institute of Technology，2009．

[ 7] 陳茂良，周軍，常燕．空間攔截攻擊區和威脅區仿真研究[J]．航天控制，2009，27(1)：41-44． CHEN Mao-liang，ZHOU Jun，CHANG Yan．Simulation of Space Interception Attack Area and Threat Area [J]．Aerospace Control，2009，27(1)：41-44．

[ 8] 張鵬宇．空間攔截最優軌道設計[D]．哈爾濱：哈爾濱工業大學，2009． ZHANG Peng-yu．Optimal Trajectory Design of Space Interception [D]．Harbin：Harbin Institute of Technology，2009．

[ 9] 崔平遠，尚海濱，欒恩杰．星際小推力轉移任務發射機會的快速搜索方法[J]．宇航學報，2008，29(1)：40-45. CUI Ping-yuan，SHANG Hai-bin，LAUN En-jie．Quick Search Method of Launch Opportunity for Interplanetary Small Thrust Transfer Mission [J]．Acta Astronautica，2008，29(1)：40-45．

[10] Howard D Curtis．Orbital Mechanics [M]．Beijing：Science Press，2009．

[11] 唐國金，羅亞中，雍恩米．航天器軌跡優化理論、方法及應用[M]．北京：科學出版社，2012． TANG Guo-jin，LUO Ya-zhong，YONG En-mi．Theory，Method and Application of Spacecraft Trajectory Optimization [M]．Beijing：Science Press，2012．

[12] 張柏楠．航天器交會對接任務分析與設計[M]．北京：科學出版社，2011． ZHANG Bai-nan．Analysis and Design of Spacecraft Rendezvous and Docking Mission [M]．Beijing：Science Press，2011．

[13] 袁建平，和興鎖．航天器軌道機動動力學[M]．北京：中國宇航出版社，2010． YUAN Jian-ping，HE Xing-suo．Dynamics of Spacecraft Orbit Maneuver [M]．Beijing：China Aerospace Publishing House，2010．

[14] 雷英杰，張善文，李續武，等．MATLAB遺傳算法工具箱及應用[M]．西安：西安電子科技大學出版社，2005． LEI Ying-jie，ZHANG Shan-wen，LI Xu-wu，et al．Genetic Algorithm Toolbox and Its Application [M]．Xi’an：Xidian University Press，2005．

[15] 蔡婉花，和興鎖．混合遺傳算法在航天器最優交會中的應用[J]．飛行力學，2008，26(4)：77-80． CAI Wan-hua，HE Xing-suo．Application of Hybrid Genetic Algorithm in Optimal Rendezvous of Spacecraft [J]．Flight Dynamics，2008，26(4)：77-80．

[16] 范淑梅．基于自適應遺傳算法的航天器快速軌道機動研究[D]．濟南：山東大學，2008． FAN Shu-mei．Research on Fast Orbit Maneuver of Spacecraft Based on Adaptive Genetic Algorithm [D]．Jinan: Shandong University，2008．

Optimal Design of Berthing Orbit for Fast Space Rendezvous

WEI Peng-tao

(The Rocket Force Command College,Hubei Wuhan 430012,China)

For the problem of fast space rendezvous, a new method is adopted for transfer ring rendezvous about berthing orbit. The optimal problem of berthing orbit is described mathematically and an optimal model is established for berthing orbit. Simulation with genetic algorithm is carried out and the results show that the designed berthing orbit can meet the demand of fast space rendezvous.

space orbit; quickly rendezvous; parking(berthing) orbit; optimum design; mathematical model; genetic algorithm

2016-04-13；

2016-06-23 作者簡介：魏鵬濤(1983-)，男，陜西白水人。講師，博士，主要研究方向為飛行動力學與制導理論。

10.3969/j.issn.1009-086x.2017.01.005

V412.4+1

A

1009-086X(2017)-01-0022-06

通信地址：430012 湖北武漢江岸區二七路145號 E-mail：weipengtao09@163.com