基于EMD的GM-LSSVM在變形預測中的應用

陸杰，梁月吉，徐寧輝，陶健春

(1.南寧勘察測繪地理信息院，廣西 南寧 530001； 2.桂林理工大學測繪地理信息學院，廣西 桂林 541004； 3.廣西城市建設學校，廣西 桂林 541003)

基于EMD的GM-LSSVM在變形預測中的應用

陸杰1*，梁月吉2，徐寧輝1，陶健春3

(1.南寧勘察測繪地理信息院，廣西 南寧 530001； 2.桂林理工大學測繪地理信息學院，廣西 桂林 541004； 3.廣西城市建設學校，廣西 桂林 541003)

針對變形呈非線性、隨機性變化特征，提出了一種基于經驗模態分解(EMD)的灰色最小二乘支持向量機(GM-LSSVM)變形預測模型。該模型首先采用EMD有效分離出隱含在變形序列中的非線性高頻成分和低頻成分；然后根據各分量特點構建了高頻LSSVM預測模型和低頻GM(1，1)預測模型，最后疊加各分量預測值得到預測結果。經理論分析和算例表明，并與灰色GM(1，1)、BP神經網絡和LSSVM對比分析。結果表明，EMD能夠有效分離變形序列的不同頻率成分，本文方法具有較強的預測精度，均方根誤差為 0.40 mm，在變形預測中具有一定的實用價值。

大壩變形；經驗模態分解；GM(1，1)；最小二乘支持向量機；精度評定

1 引 言

大壩變形往往受水位、溫度等多種因素共同影響，具有一定的非線性和隨機性變化，為保證大壩以及人類的安全，需要及時掌握大壩變形狀態并及時做出準確預測。目前，常用的預測方法主要有時間序列分析、灰色理論、BP神經網絡和支持向量機等，以上方法均存在一定的局限性。灰色預測模型具有所需數據少、建模簡單等特點，適合用于解決呈指數增長趨勢的實際問題，而對于復雜變化、隨機變化的序列，預測誤差較大[1]；人工神經網絡在大壩變形分析中得到了較為廣泛的應用[2]，但其易陷入局部極小點、模型結構不易確定、泛化能力不強或過于學習等。趙洪波等[3]將支持向量機引用到變形預測中，解決了多因素影響下的復雜變形預測問題，預測精度得到了進一步提高。然而，由于大壩變形受多種因素共同影響，直接通過建立變形量與影響因素之間的復雜非線性關系模型難以保證模型預測的準確性。 Huang等[4]于1998年提出了一種新的信號處理EMD方法。該方法是一種處理非線性和非平穩信號的自適應分解方法，不需要確定任何函數，直接對信號進行平穩化處理，能夠有效提取原信號的波動項和趨勢項[5]。基于上述研究，本文提出了基于經驗模態分解(EMD)和灰色最小二乘支持向量機(GM-LSSVM)的大壩變形預測方法。通過算例，證實其有效性和可行性。

2 基于EMD的GM-LSSVM變形預報模型

2.1 經驗模態分解法

經驗模態分解(Empirical Mode Decomposition，EMD)是一種自適應信號分解方法，能夠將存在于原始序列中不同特征的趨勢逐級篩選出來，得到具有相同特征尺度的固有模態分量(Intrinsic Mode Function，IMF)，IMF必須同時滿足兩個條件[4，5]：第一，在待分解信號中，極值點的數目與過零點的數目相等，或最多相差一個；第二，在任一時間上，由局部極大值和局部極小值定義的包絡均值為零。具體分解過程可參考文獻[4，5]。2.2 灰色GM(1，1)

灰色GM(1，1)是一個單個變量預測的一階微分方程模型，其離散時間響應函數近似指數規律。建模的思路：大壩水平位移變形序列經過一次累加，形成一個遞增數列，經不斷累加，形成的數據點連線后接近于某個指數函數，然后通過這個指數函數外推到下一個累加和，再累減還原即得到大壩序列預測值。

2.3 最小二乘支持向量機

設某變形序列的樣本集為{(xi，yi)|xi∈Rn，yi∈R，i=1，2，…，l)}，得到LS-SVM的回歸函數為[6]：

y(x)=wTφ(x)+b

(1)

式中，φ(x)表示能夠滿足Mercer條件的核函數，w表示超平面的權值向量，b表示偏置頂。

對于最小二乘支持向量機的估計問題，將回歸問題等價為最小化得到：

(2)

式中，γ表示正則化參數，ei表示誤差項。構建式(2)的Lagrange函數得到：

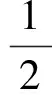
(3)

式中，a=[a1，a2，…，al]T。根據 KKT(Karush-Kuhn-Tucker)條件，計算Lagrange函數的最優解：

(4)

對式(4)進行簡化，得到的線性方程組為：

(5)

式中，y=[y1，y2，…，yl]T，A=[1，…，1]T，I表示單位矩陣，K(xi，yi)表示滿足Mercer條件的核函數。

設B=K(xi，yi)+γ-1I，采用最小二乘運算求解式(5)得到：

(6)

得到LSSVM的估計函數為：

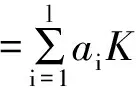
(7)

2.4 LSSVM參數的優化

由2.3可知，核函數k()的選擇以及核參數σ和正則化參數γ的優化直接影響到最小二乘支持向量機的預測精度。因此，本文選取徑向基函數作為模型的核函數，該核函數能夠較好地反映模型的復雜程度，采用網格搜索法對σ和γ參數進行優化。參數優化步驟如下[7]：

(1)設定參數σ和γ的選擇范圍、參數步長、網格間隔、網格點目標函數值的計算等。

(2)根據σ和γ的初始值，選擇第一個交叉驗證網點位置，通過交叉驗證方法獲取訓練均方誤差作為網格點計算的目標函數，并計算所有的網格點。

(3)選取均方誤差最低的一組(σ，γ)為最優參數。若選取的參數達不到精度要求，則以選擇的參數為中心網格點，在較小的范圍內構建新的二維網格平面重新計算目標函數，再次選取均方誤差最低的參數。如果滿足精度要求，則停止，否則繼續重復以上步驟，最終獲取精確的參數σ和γ作為最優值。

2.5 預測流程

本文模型預測流程如下：

(1)采用EMD對大壩變形序列進行分解，得到n個IMF高頻分量和1個低頻分量DF。

(2)針對各IMF，建立相應的LSSVM預測模型，同時建立灰色GM(1，1)預測模型對DF低頻序列進行預測。

(3)對各模分量預測的殘差進行組合即得到最終的預測結果。

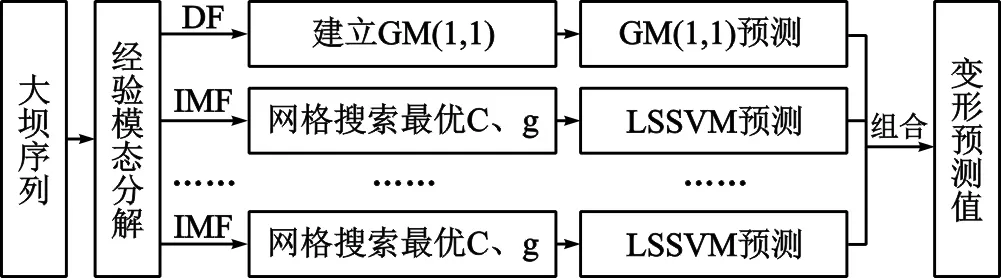
圖1 模型預測流程圖

3 模型精度評定

本文采用均方根誤差和平均絕對值誤差來評定模型預測精度[1]：

(8)

(9)

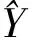
4 算例分析

本文以某大壩水平位移變形監測數據為實驗數據[9]，監測期為91期，如圖2所示。可見，該大壩水平位移變形變化不穩定，非線性和隨機性變化較強，難以直接建立較為準確的預報模型。因此，為探討大壩變形序列的特征，采用EMD進行分解，分解結果如圖3所示。由圖3可見，EMD將變形序列分解為4個頻率依次降低的分量，其中IMF1分量具有一定的非線性變化，IMF2和IMF3呈現出周期性和隨機性成分，DF體現出變形序列的整體變化趨勢。顯然，根據各分量建立對應的模型，對提高預測精度具有較大的可能。

為驗證本文方法的有效性和可行性，建立4種方案進行對比分析：方案1—灰色GM(1，1)預測模型、方案2—BP神經網絡預測模型、方案3—最小二乘支持向量機預測模型、方案4—基于EMD的GM-LSSVM預測模型。各方案采用前71期變形數據作為模型訓練輸入，后20期作為模型預測數據。方案1～方案3直接采用原始變形預測進行建模，方案4采用經EMD分解得到的各分量進行建模。同時，為了減少建模誤差，本文統一將變形序列歸化到[-1，1]區間，再進行建模預測。各分量的預測結果圖4所示。

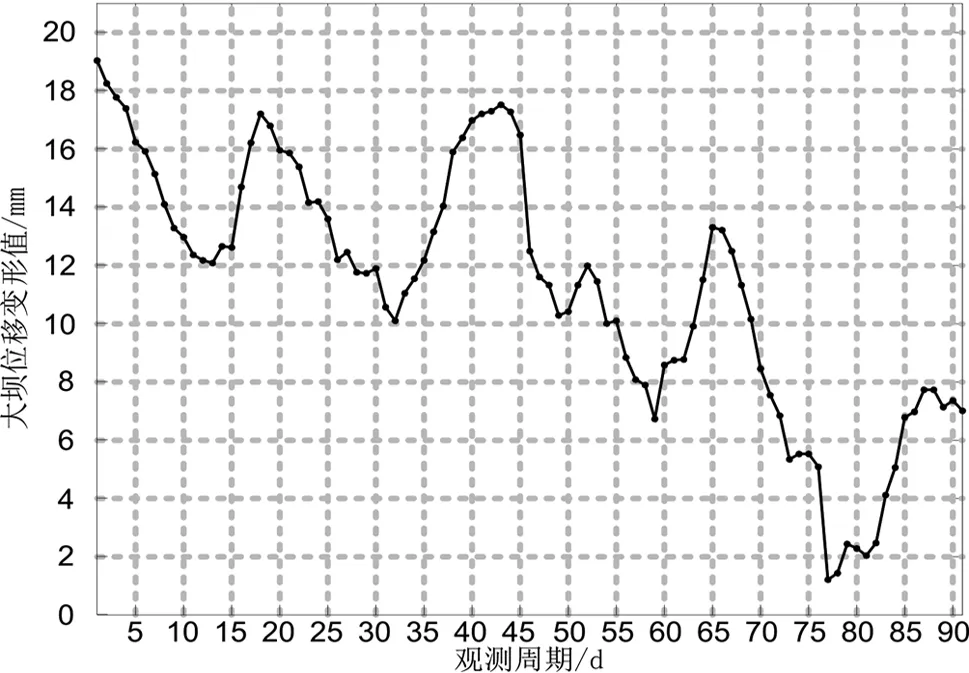
圖2 大壩變形水平位移序列

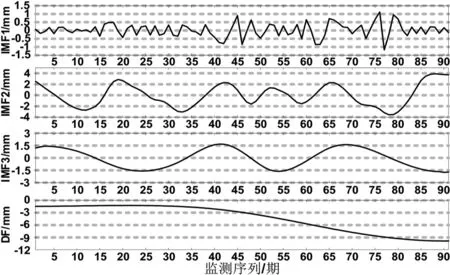
圖3 EMD分解結果

圖4 各分量預測值和實際值對比

由圖4可得，方案4的預測結果和實際分量相吻合，預測精度較高。各方案預測結果如表1和圖5所示。

由表1可見，方案1、方案2和方案3的預測結果不穩定，部分預測值和實際值相差比較大，GM(1，1)的最大殘差為 4.33 mm，BP神經網絡的最大殘差達到 3.96 mm，LSSVM的最大殘差為 2.73 mm。而方案4的預測結果均優于其他方案，殘差最小值為 0.04 mm，最大值僅為 0.81 mm。結合圖5進一步看出：GM(1，1)不能正確反映變形的趨勢，過于線性擬合預測；BP神經網絡由于自身的缺陷，預測結果波動較大；LSSVM的部分預測結果不穩定，而本文方法的預測結果比較穩定，接近于大壩實際值。可見，采用經驗模態分解離使得變形序列中不同頻率的成分得到有效分離，預測模型的自身性能得到充分發揮。本文方法綜合結合線性和非線性的擬合能力，預測結果更能顯示大壩變形的趨勢。

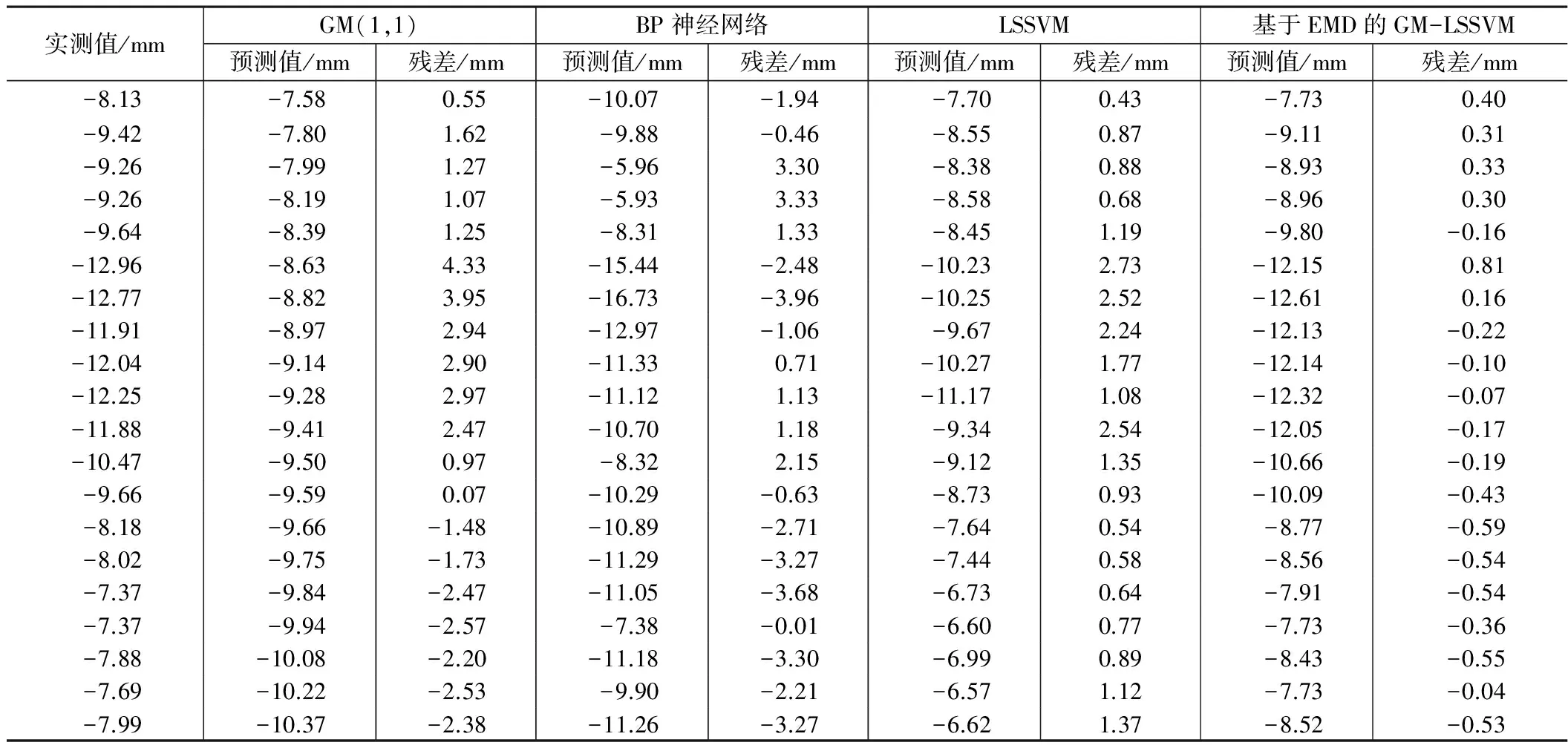
不同方案的預測結果對比 表1

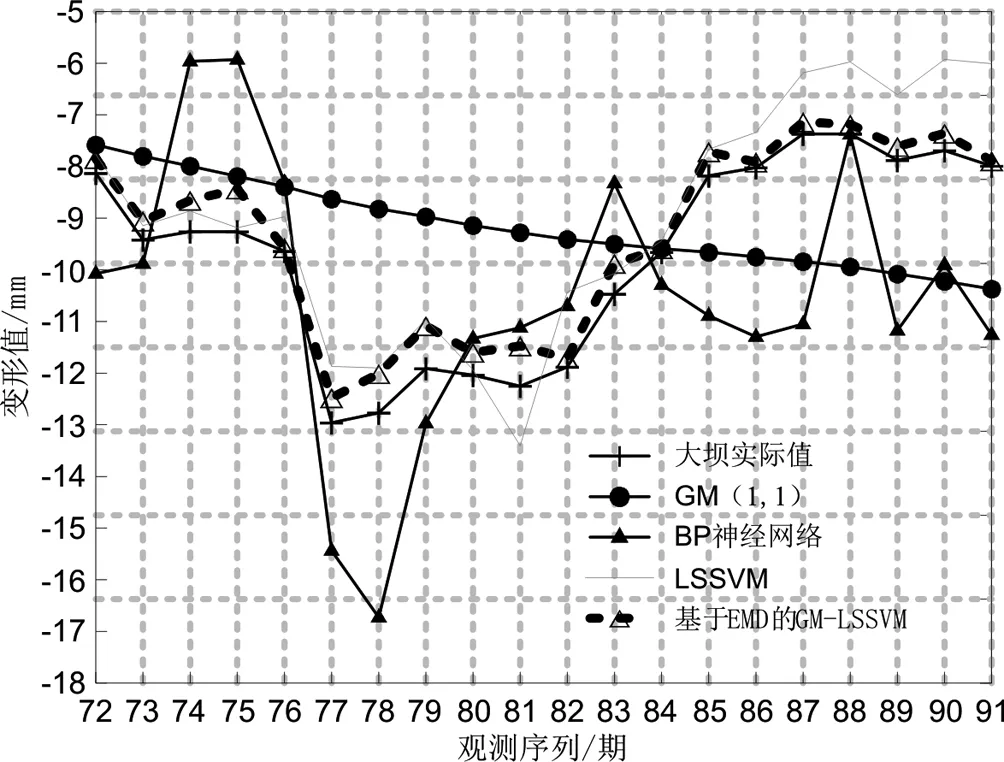
圖5 各方案的預測值和大壩實際變形值對比

各方案的預測精度統計如表2所示。

各模型精度對比(單位/mm) 表2

由表2進一步發現，方案4的預測精度最高，均方根誤差和平均絕對誤差分別為 0.40 mm、 0.34 mm。可見，基于EMD的GM-LSSVM預測模型保證了較好的全局預測精度，更具優越性。綜上，采用經驗模態分解能夠有效分離隱含在變形序列中的特征成分，更有利于模型的建立和預報。正是本文方法綜合考慮了變形的特征，充分發揮了模型的線性和非線性預測能力，無論在預測結果還是預測精度上均優于單一的GM(1，1)、BP神經網絡和最小二乘支持向量機。

4 結 論

本文提出基于EMD的GM-LSSVM變形預測方法，結果表明：經驗模態分解能夠有效分離隱含在時序中隱含的非線性和隨機性高頻成分以及趨勢低頻成分；各分量更加明顯地表現出時序中隱含的特征信息，使得GM-LSSVM預測模型的自身性能得到充分發揮。本文方法具有較強的擬合預測能力，預測精度較高。

[1] 任超，梁月吉，龐光鋒等. 最優非負變權組合模型在大壩變形中的應用[J]. 大地測量與地球動力學，2014，34(6)：162～166.

[2] 劉勇健，李彰明，張建龍等. 基于遺傳-神經網絡的深基坑變形實時預報方法研究[J]. 巖石力學與工程學報，2004，23(6)：1010～1014.

[3] 趙洪波. 支持向量機在隧道圍巖變形預測中的應用[J]. 巖石力學與工程學報，2005，24(4)：649～653.

[4] Huang N E，Shen Z，Long S R. The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J]. Proceedings of the Royal Society of London SERIESA，1998，903～995.

[5] 戴吾蛟，丁曉利，朱建軍等. 基于經驗模式分解的濾波去噪法及其在 GPS多路徑效應中的應用[J]. 測繪學報，2006，35(4)：321～327.[6] Suykens J A K，Vandewalle J. Least Squaresupport Vector Machine Classifiers[J]. Neural Processing Letters，1999，9(3)：293～300.

[7] Liu Xianglou，Jia Dongxu，Li Hui. Research on Kernel Parameter Optimization of Support Vector Machine in Speaker Recognition[J]. Science Technology and Engineering，2010，10(7)：1669～1673.

[8] 姜成科. 基于遺傳算法的神經網絡在大壩變形預報中的應用[D]. 大連：大連理工大學，2009.

GM-LSSVM Based on EMD in The Application of the Dam Deformation

Lu Jie1，Liang Yueji2，Xu Ninghui1，Tao Jianchun3

(1.Nanning Exploration & Survey Geoinformation Institute，Guilin 530001，China； 2.College of Geomatics and Geoinformation，Guilin University of Technology，Guilin 541004，China； 3.Guangxi Urban Construction School，Guilin 541003，China)

A new algorithm based on empirical mode decomposition (EMD)and the grey least squares support vector machine (GM-LSSVM)for dam deformation prediction was presented. Firstly，to effectively separate the nonlinear trend of volatility of high frequency component and low frequency one，the algorithm deformation sequence was decomposed by EMD；Then，the LSSVM was applied to build a prediction model for high frequency component，and the GM(1，1)was applied to build a prediction model for low frequency one；Finally，the predicted values of each component in the forecast was overlay. The calculation result was analyzed and compared with the grey GM(1，1)、BP neural network and LSSVM. The results show that the EMD can effectively separate different frequency components of deformation sequence，prediction accuracy of the method is stronger，root mean square error is 0.40mm，which can be applied to dam deformation prediction practically.

dam deformation；empirical mode decomposition；GM (1，1)；least squares support vector machine；precision evaluation

1672-8262(2017)01-142-04

P196，TV698.11

B

2016—05—07 作者簡介：陸杰(1978—)，男，工程師，主要從事測繪工程技術工作。 基金項目：廣西自然科學基金項目(2014GXNSFAA118288)；廣西“八桂學者”崗位專項經費資助項目、廣西空間信息與測繪重點實驗室資助課題(桂科能130511402，130511407)。