基于多元回歸法的武漢市二手房價格影響因素研究

繆格，李英冰，袁菲

(1.武漢大學測繪學院，湖北 武漢 430079； 2.武漢大學測繪學院時空大數據研究中心，湖北 武漢 430079)

基于多元回歸法的武漢市二手房價格影響因素研究

繆格1*，李英冰1，2，袁菲1

(1.武漢大學測繪學院，湖北 武漢 430079； 2.武漢大學測繪學院時空大數據研究中心，湖北 武漢 430079)

二手房價格受到區域因素、房屋自身因素、市場因素等多種因素綜合影響，傳統估價方法過多關注于房地產自身屬性的差異及修正，有較強的主觀性。本文以特征價格模型為基礎，采用多元線性回歸模型和多元對數回歸模型，建立二手房價格與區位因素、房屋自身因素等影響因子之間的函數關系，并采用武漢市二手房掛牌數據、看房價網(www.kanfangjia.cn)數據和百度熱點數據，對武漢市二手房各個特征變量進行篩選、量化和整合，并對比分析不同區域各個特征變量對二手房價格的影響程度，實驗結果與實際情況符合度較好。

二手房；特征價格；價格評估；影響因素；多元回歸法

1 引 言

二手房價格是政府和廣大人民的關注焦點，而如何給出相對客觀價格，受到研究人員和市場交易的廣泛關注。傳統的房價評估方法常用的是市場比較法、收益還原法和成本法，但在實踐中往往依賴評估師的經驗，對數理模型的運用比較少[1]。Cour最早提出特征價格模型，當時多用于耐用消費品的定價[2]。特征價格模型從產品的差異性出發，把二手房產品價格分解為各個特征價格，核心在于建立二手房特征與價格之間的函數關系[2]。特征價格模型將房屋價格特征化能讓消費者更能理解房價構成，購房者可以根據自己的需求與經濟狀況有針對性地選擇自己想要的居住環境；此外，從消費者的需求角度出發，從房屋特征的角度看待房屋價格，在一定程度上反映出消費者對房屋特征變量的關心程度，使房價的評估更為簡易，為政府等有關部門提供借鑒[3]。

特征價格模型自提出以來，被國內外研究不斷深入且緊密聯系實際開展研究。1999年，Paliwal等基于特征價格模型，引入三角模糊數法衡量人們對土地購買的意愿[4]；Peterson(2009)將人工神經網絡法與特征價格模型相結合[5]；Badi H.Baltagi(2011)用極大似然估計擬合了特征價格模型[6]。國內學者最早是由中國人民大學蔣一軍、龔江輝(1996)利用特征價格方法提出了計算異質商品價格指數的方法，并將其應用于房地產價格指數的計算[7]，溫海珍(2003)開啟了國內特征價格模型實證研究之路，對杭州市二手房交易案例進行數據整合，研究特征影響變量[8]；黃古博、李雨真(2011)應用主成分法改進二手房的特征價格模型，排除變量間因多重共線性產生的誤差[9]；李恒凱(2012)結合地理信息系統(GIS)和主成分分析(PCA)算法研究如何提高二手房特征價格模型函數擬合效果及準確性[10]。

二手房價格往往受到多種因素的影響，特征價格模型將二手房價格分解為各個特征價格，得出各個特征對二手房價格的影響，從而實現二手房價格的估算。本文采用特征價格模型，從消費需求出發，用多元回歸分析法將房價分解為各個特征價格來研究房價的影響因素，其中通過逐步回歸和變量整合以避免變量間的多重共線性，從理論上分析二者的函數關系。

2 特征價格模型的構建

2.1 特征價格模型理論及參數估計

二手房的真正效用源自于其包含的各個分散的功效特征，如面積、樓齡、朝向，如果二手房所包含的特征不同，則相應的價格也不同。消費者愿意為二手房的某個特征的每單位增加而支付的額外費用，則稱為該特征的隱含價格(特征價格)，它反映了各個特征對二手房價格的貢獻程度。構建回歸函數是特征價格模型的研究的核心，Butler理論闡述房屋價格受區位特征(L)、建筑特征(S)、鄰里環境(N)三大特征變量影響[11]：

P=f(L，S，N)

(1)

在其他條件不變前提下，將每個特征求偏導即為邊際隱含特征價格。國外文獻出現最頻繁的模型變量為面積，總層數，裝修程度，有無CBD，公交站，有無地鐵，樓齡，教育設施與生活、娛樂設施等[1]。在函數形式的設定中，最常用的函數形式為線性形式和對數形式，計算公式分別為式(2)和式(3)：

P=α0+∑αiZi+ε

(2)

ln(P)=α0+∑αiln(Zi)+ε

(3)

其中P是特征價格，Zi是住房的特征變量，αi是常數項，ε是隨機干擾項。

對數模型中，自變量和因變量以對數形式進入模型，則回歸系數對應著特征的價格彈性。對數模型是假設函數經過顯性化處理后得到的表達，對數模型考慮到了二手房特征應當遵循邊際效用遞減規律，即房屋價格隨某種特征的增加而增加，但增加速率會越來越慢，對數模型能較好地反映價格與各個特征之間的函數關系。

經典線性計量經濟學模型最常用的最小二乘法實現參數估計法的應用。參數的最小二乘估計(OLS)：選擇合適的參數αi使得全部樣本值的殘差平方和(Rss)最小，即

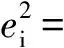
(4)

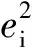
Yi——為樣本的真實值

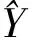
線性、無偏性、最小方差性是運用最小二乘法所得的多元線性回歸參數估計值所具有的特性[2]。

2.2 模型變量的選取與量化

選取房價相應的解釋變量是在對武漢市二手房價格分析建模前必須考慮的步驟。根據已有的數據及后期可以獲取到的數據，結合國內外特征價格模型常用的解釋變量，初步選取室廳、面積、有無景點、首付、層數、有無車庫、總層數、朝向、樓齡、有無地鐵、裝修程度、學校、公園、CBD、公交線路、醫院、商場這17個解釋變量研究。

特征變量，詳細信息主要包括室廳、面積、總層數、朝向、裝修程度、樓齡、學校、公園、醫院、商場、中央商務區(CBD)、有無地鐵等解釋變量。

二手房的特征變量分定量、定性變量，為了從數理模型是研究各個特征變量對二手房價格產生的影響，需要將各個變量進行量化整合，不同類別的變量量化方式不同，如表1所示。

住宅解釋變量的初步選取 表1

(1)定性變量的量化

定性變量用三種方法來量化，即虛擬變量量化法、李克特量表量化法和綜合性指標量化法[3]，具體量化法如表2所示：

定性變量量化表 表2

表2中，地鐵凸顯了交通的便捷程度，因此二手房周圍有地鐵也會讓房價相應提升，預期影響為正；其次，將裝修程度量化為四個等級，裝修程度越高，表明住宅的成本價格越高，住宅價格也越高。

當特征變量選取較多時，自變量之間可能存在較大的相關性，為了避免自變量的多重共線性問題，采用綜合性指標量化法來進行特征變量的整合以減少變量數目。

(2)定量變量的量化

二手房價格、面積、樓齡、室廳數、層數、總層數、公交站數這7個定量變量直接用實際數值(對數模型中對二手房面積進行簡單的自然對數變換)進行量化，如表3所示，變量內涵也比較簡單客觀[1]。

定量變量量化表 表3

小區周圍公交站個數越多，居民出行越方便，住宅價格越高。樓齡是住宅竣工日期到2016年的時間段長度，計量單位為年，例如2015年竣工的住宅樓齡為1，樓齡反映建筑本身的新舊與使用程度，樓齡與住宅價格呈負相關關系。

變量經過整合和量化后，初步確定進入模型的特征變量有12個。

2.3 模型變量的剔除與篩選

由于初步選擇的特征變量較多，特征變量之間可能存在比較嚴重的線性關系，上述采用綜合性指標方法量化部分變量克服自變量之間的多重共線性，本文還采用逐步回歸法，逐步回歸是向前回歸法和向后回歸法的結合，首先按自變量對因變量的貢獻率進行排序，按照從大到小的順序選擇進入模型的變量。每將一個變量加入或刪除模型(步進)時，要進行偏F檢驗，剔除不顯著的變量，然后再對留在模型中的變量進行檢驗，直到沒有變量可以納入，也沒有變量可以剔除為止，從而盡量排除變量多重共線的可能性。步進準則中，F檢驗的概率≤0.050表示自變量對因變量的影響顯著，判斷結果為進入(enter)模型；F檢驗的概率≥0.100表示自變量對因變量的影響為不顯著，判斷結果為移出(remove)模型。

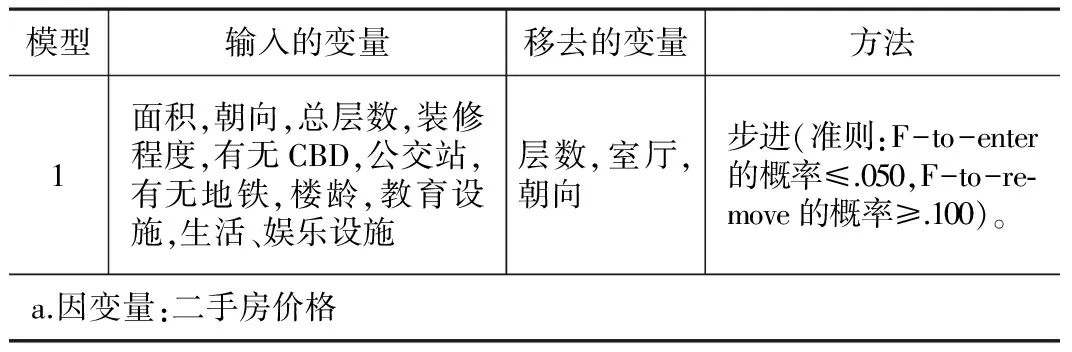
模型構建最終確定的特征變量 表4

由表4可見，被移去的變量有層數，室廳和朝向，可能是因為研究的數據中包含一定量的商鋪，使得一些自變量與因變量的函數關系不明顯。最終進入回歸模型的特征變量共9個，分別是面積，總層數，裝修程度，有無CBD，公交站，有無地鐵，樓齡，教育設施與生活、娛樂設施。

量化整合修正后共有9個特征變量，將其逐步導入模型，當9個特征變量全部導入模型時，模型的擬合效果最好。所以，最終確定的解釋變量分別是面積，總層數，裝修程度，有無CBD，公交站，有無地鐵，樓齡，教育設施與生活、娛樂設施。

3 實證研究

3.1 實驗數據說明

武漢市近幾年房價成穩定增長趨勢，且武漢市各區域房價差異較大，本文選取了2015年武漢市10個區二手房交易掛牌數據2 000個進行研究。

通過對數據的統計分析，刪除不符合常理的數據記錄后，分別作各個自變量與因變量的箱線圖，如圖1所示：橫坐標表示二手房的建成年份(年)，反映出二手房的樓齡，縱坐標表示所研究的二手房價格(萬元/m2)。

箱線圖利用數據中的5個統計量：最小值、第一四分位數、中位數、第三四分位數與最大值來描述、判斷數據異常值，從中鑒別出離群值和極端值。描繪個案偏離箱體邊緣(上端、下端)的距離是箱體的幾倍，其中“°”表示離群點(1.5倍～3倍)，“*”表示極端離群點(超過3倍)，然后進行異常值剔除后，最后采用的樣本數為 1 494個。

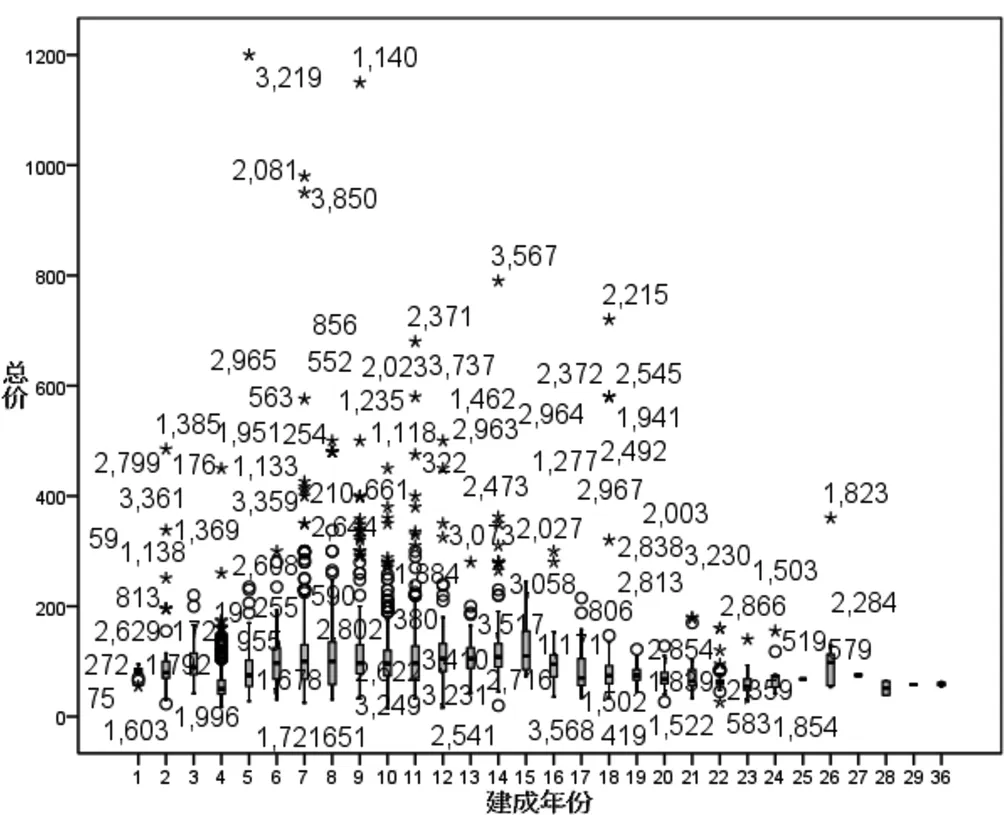
圖1 二手房總價與二手房建成年份箱線圖

3.2 擬合分析與自相關DW檢驗

當選取的9個特征變量全部進入模型時擬合效果最好，多元回歸分析結果如表5所示，R代表復相關系數，在多元回歸中，為了避免擬合效果單調隨變量X的增加而變大，R(a)更能體現擬合和方程的顯著性檢驗。R的平方即R2表示回歸方程對樣本觀測值的擬合程度，越接近于1，方程的擬合度越高。線性模型與對數線性模型的復相關系數分別為0.927，0.935。當給模型增加自變量時，復決定系數也隨之逐步增大，當自變量足夠多時會得到模型擬合良好，而實際卻可能并非如此，于是考慮對R2進行調整，稱調整R2，分別為0.858，0.873；模型所能解釋因變量差異的百分比都大于85%，自變量和因變量間表現出較良好的線性關系，有較好的模型解釋能力。但線性模型的標準估計誤差遠遠高于對數模型，且對數模型的解釋力度更強，經對比可見，對數線性模型具有更好的解釋力。

估計標準誤差是說明實際值與其估計值之間相對偏離程度的指標，主要用來衡量回歸方程的代表性，對數模型的誤差值遠小于線性模型，對數模型方程代表性更優。

更改后的F檢驗值分別為905.605、1144.248，sig顯著性水平都為0.000，小于0.05，則F檢驗通過，表示統計量顯著，方程中自變量因變量間線性關系能夠成立，模型對樣本數據的擬合在統計上有意義。

多元線性回歸分析的一個假定是誤差項的相互獨立性，要驗證在誤差之間是否存在自相關聯系效應，避免導致線性回歸分析出現嚴重的偏誤，所以用較為精確的自相關檢驗方法——自相關DW檢驗來考察，兩個回歸方程的DW檢驗值，分別為1.820和1.744，都接近于2，可認為兩個模型中的誤差項基本上是獨立的，基本不存在異方差問題，如表5所示。

多元回歸分析結果的擬合優度表 表5

3.3 多重共線性檢驗與回歸方程分析

多元系數回歸如表6所示。B值是指回歸系數和截距，常數則代表截距，變量對應的B值代表回歸系數。

標準誤差用來衡量抽樣誤差，越小表明樣本對總體越有代表性，用樣本推斷總體參數的可靠度越大。經對比可見，對數模型中的標準誤差遠小于線性模型，說明對數模型二手房價格回歸方程房價預測可靠性較好。

標準化回歸系數是指去除了因變量Y和自變量X1，X2，…Xn量綱影響之后的回歸系數，其絕對值的大小直接反映了Xi對Y的影響程度。

VIF為方差膨脹因子，用于檢驗自變量的多重共線性，標準為10，超過10即表明自變量間存在較嚴重的多重共線性，表中VIF最大為2.152，遠遠小于10，可認為自變量間不存在顯著的多重共線性，如表6所示。

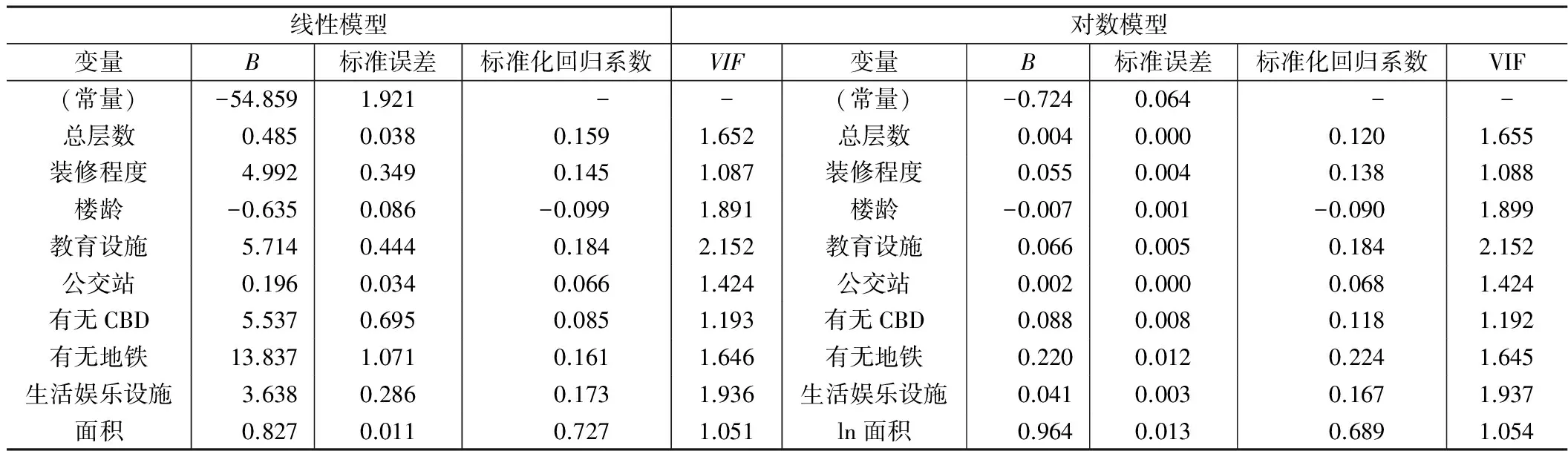
多元回歸系數表 表6

由上述多元線性回歸分析回歸系數表可知，最終的回歸方程為：

(2)線性模型多元回歸方程：

P=-54.859+0.485X1+4.922X2-0.635X3+5.741X4+0.196X5+5.537X6+13.837X7+3.638X8+0.827X9

(5)

(3)對數模型多元回歸方程：

LnP=-0.724+0.004X1+0.055X2-0.007X3+0.066X4+0.002X5+0.088X6+0.220X7+0.041X8+0.964LnX9

(6)

式(5)與式(6)為多元線性回歸分析最終確定的回歸方程，其中，P代表二手房價格，X1，X2，…X9分別代表總層數、裝修程度、樓齡、教育設施、公交站、有無CBD、有無地鐵、生活、娛樂設施和面積。對各個特征變量對房價的預期影響進行回歸參數公式符號的驗證分析，驗證結果符合預期值。經過對比，線性模型中各項標準誤差較大，可能是因為定量變量面積的數值較大，從而引起了數值較小的定性變量的回歸參數的畸變。對數模型各個回歸參數的標準誤差遠遠小于線性模型，在一定程度上反映出對數模型有更好的解釋能力。

3.4 殘差分析與模型應用

(1)殘差分析

在模型假定基礎上建立判定系數的計算和顯著性檢驗，這就考慮到模型的假定基礎的真實性問題。如果模型的假定不真實，那么模型的適用性就遭受懷疑，殘差分析是證實模型假定真實性的基本方法，兩個模型的絕大多數標準化殘差隨機落于-2和+2之間，滿足方差齊次性的假設，可認為兩個模型的假定都合理。

(2)參數回代差價分析

目前共有1 494個武漢市二手房樣本案例，通過所得出的兩個模型回歸公式做參數回代，得出計算出的理論價格，并且與相應的實際二手房價格做差價作為橫坐標，縱坐標為差價數值出現的頻率，形成頻率分布直方圖，如圖2所示：

圖2 武漢市線性模型與對數模型差價頻率直方圖

線性模型和對數模型分別對應差價頻率直方圖都滿足正態分布，每平方米價格差價大多數都集中在 1 500元以內，對比可見對數模型的差價頻率曲線更為陡峭，且超出 2 000元范圍的差價相比于線性模型要少得多，模型擬合效果更好。

(3)特征變量影響程度的區域分析

各個二手房特征價格的量綱不同，故采用標準化回歸系數(去除量綱)來衡量自變量的相對重要性，可將自變量對因變量的相對影響程度大小進行排序，如表7所示。

(4)實例驗證分析

隨機選取武漢市某一二手房案例來進行參數回代反算二手房價格，線性模型回歸方程案例計算出來的二手房總價差價為2萬元，二手房每平方米價格差價172元。對數模型回歸方程案例計算出來的二手房總價差價為1萬元，二手房每平方米價格差價85元，可見這個案例擬合效果不錯。從整體看，線性模型每平方米價格差價均值在870元，對數模型的每平方米價格差價均值在820元，由差價頻率分布直方圖可看出每平方米價格差價大多數分布在 1 500元以內。

對數模型下武漢各區標準化回歸系數及特征影響程度分析表 表7

4 結 論

本文基于特征價格模型，結合武漢二手房數據，采用多元回歸方法，評估了二手房價格的影響因素，主要工作與貢獻為：

(1)利用掛牌數據、看房價網數據、百度API數據查詢獲取了武漢市及其江漢區、江夏區、武昌區的二手房各個特征變量的數據并且進行篩選、量化和整合。并對影響因素進行了排序。

(2)分別構建了可供實際應用的線性模型、對數模型對二手房價格評估進行分析比較，經過模型擬合優度、標準誤差、殘差分布與差價頻率圖的對比分析，對數模型擬合效果更好，其回歸方程解釋能力更強。

在數據分析時，有些問題需要進一步研究。如有些數據仍不容易獲取，如居民的收入水平、小區環境質量、小區居民素質等，可能會導致特征變量因素不全面進而影響模型的擬合。以后的研究應重點學習如何量化人文因素與環境質量這些未有特定量化標準的特征變量。

[1] 張鑫. 基于特征價格的二手房價格評估方法研究[D]. 杭州：浙江大學，2007.

[2] Court，A T. Hedonic Price Indexes with Automotive Examples，In The Dynamics of Automobile Demand，New York：General Motors，1939.

[3] 李志輝. 基于Hedonic模型的武漢住宅特征價格研究[D]. 武漢：華中農業大學，2008.

[4] Paliwal R，Geevarghese G A，Babu P R，et al. Valuation of Landmass Degradation Using Fuzzy Hedonic Method：A Case Study of National Capital Region[J]. Environmental & Resource Economics，1999，14(4)：519～543.

[5] Jonathan P，Russell J A，Andrew G，et al. The neurophysiological bases of emotion：An fMRI study of the affective circumflex using emotion-denoting words[J]. Human Brain Mapping，2009，30(3)：883～895.

[6] Baltagi B H，Bresson G. Maximum likelihood estimation and Lagrange multiplier tests for panel seemingly unrelated regressions with spatial lag and spatial errors：An application to hedonic housing prices in Paris[J]. Journal of Urban Economics，2011，69(1)：24～42.

[7] 蔣一軍，襲江輝. 房地產價格指數與Hedonic模型[J]. 中國資產評估，1996(3)，30～32.

[8] 溫海珍，賈生華. 二手房的特征與特征的價格——基于特征價格模型的分析[J]. 浙江大學學報·工學版，2004(10)：1138～1149.

[9] 黃古博，李雨真. 基于主成分分析法的商品住宅特征價格模型改進[J]. 華中農業大學學報：社會科學版，2011(4)：93～97.

[10] 李恒凱，王秀麗，劉小生. 基于GIS和PCA的住宅房產特征價格模型[J]. 測繪科學，2012，37(2)：119～122.

[11] Butler，R V. The specification of hedonic indexes for urban housing[J]. Land Economics，1982，58，94～108.

[12] Lee J，Kwak S J，List J A. Average Derivative Estimation of Hedonic Price Models[J]. Environmental & Resource Economics，2000，16(1)：81～91.

[13] 馬思新，李昂. 基于 Hedonic模型的北京住宅價格影響因素分析[J]. 土木工程學報，2003(9)：59-64.

[14] 周麗萍. 商品住宅特征價格模型與指數的應用研究[D]. 西安：西安建筑科技大學，2008.

The Influence Factors research of Second-hand House Price in Wuhan City Based on the Multiple Regression Method

Miao Ge1，Li Yingbing1，2，Yuan Fei1

(1.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China； 2.Spatial-temporal Big Data Research Center，School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China)

Second hand housing prices are subject to regional factors，housing factors，market factors and other factors. A lot of attentions are paid to the real estate property of the differences and amendments for the traditional evaluation methods. There is a strong subjectivity. Based on hedonic price model，the multiple linear regression model and multiple regression model are used to establish the function relationship between the price of second-hand house and location factors，housing factors and other influencing factors. By using Wuhan second-hand housing listing data，the data from the website of kanfangjia (www. kanfangjia. cn)，and the data form the website of Baidu，making the screening，quantification and integration the various characteristics of second-hand housing variables of Wuhan，and to compare and analyze the influence degree of each characteristic variable on the price of second-hand house，and the results of the experiment fit well with the actual situation.

second hand housing；hedonic price；price evaluation；influencing factor；multiple regression method

1672-8262(2017)01-33-06

P208.2

A

2016—08—17 作者簡介：繆格(1994—)，女，碩士研究生，研究方向為時空大數據分析。 基金項目：武漢市住房保障和房屋管理局信息化建設項目：“智慧房管”主數據庫設計及一期建庫WHZC-2014-075A(2210、2415、2416)