流形與成對約束聯合正則化半監督分類方法*

奚 臣，錢鵬江，顧曉清，蔣亦樟

江南大學 數字媒體學院，江蘇 無錫 214122

流形與成對約束聯合正則化半監督分類方法*

奚 臣+，錢鵬江，顧曉清，蔣亦樟

江南大學 數字媒體學院，江蘇 無錫 214122

半監督學習方法主要通過學習少量標記樣本和大量未標記樣本知識來提高學習效果，然而目前許多半監督方法注重在未標記樣本的利用上深耕，忽略了對標記樣本等監督信息的繼續研究。鑒于此，結合流形正則化框架提出了一種流形與成對約束聯合正則化半監督分類方法（semi-supervised classification method based on joint regularization of manifold and pairwise constraints，SSC-JRMPC）。SSC-JRMPC從兩個方面進行研究：一方面該方法繼承了流形正則化框架中的特點，將經驗風險和結構風險最小化，以及對整個數據的內在數據分布進行運用；另一方面，通過將樣本標簽轉化為成對約束的形式，并把這些擴展的知識并入到目標公式中來進一步探索監督信息包含的知識，一定程度上提高了SSC-JRMPC算法的分類準確性。通過在真實數據集上的實驗，驗證了上述優點。

半監督學習；分類；流形正則化；成對約束

1 引言

半監督學習是一種結合有監督學習和無監督學習的方法，其學習的基本假定是樣本數據和要劃分的類別已知，并且具有一定數量的類別已知的樣本和大量類別未知的樣本。半監督分類利用大量未標記數據擴大分類算法的訓練集，主要從有監督學習的角度出發，當已標記訓練樣本不足時，研究如何自動地利用大量未標記樣本信息輔助分類器的訓練。

普遍來說，學者在研究時通常都是通過兩個方面來提高半監督分類器的性能：一是利用高效手段學習這些少量的標記樣本等監督信息，這通常都是借鑒監督學習的手段來實現的；二是利用有效學習方法來挖掘未標記樣本中所蘊含的大量可用信息，流形學習方法就是一種有效的手段，它利用一些分布上的假設或者樣本之間的內在聯系，將未標記樣本轉化為標記樣本，然后合并到標記的數據中，擴大可用的訓練數據集，從而使分類器的性能更優異。同時，在半監督學習中，數據標簽（class labels）[1-9]作為最為常見且直接的先驗知識類型而被普遍利用；成對約束（pairwiseconstraints）[10-12]又稱必須關聯（must-link）和不可能關聯（cannot-link）約束，屬于另一種監督信息類型，相對而言具有更大的靈活性和實用性。實際情況下有可能只給出了成對約束而沒有數據標簽，成對約束可以是事先給定的，也可以是由數據標簽轉化而來的。

支持向量機（support vector machine，SVM）是Vapnik在統計學習理論[13]基礎上發展起來的針對小樣本的機器學習方法。該方法由于具有較強的泛化能力，方便對高維數據操作而得到了日益廣泛的研究和應用。學者也基于SVM研究衍生出一些半監督支持向量機算法[4，14-18]，比較典型的有半監督支持向量機（semi-supervised SVM，S3VM）[4]，它基于聚類假設，試圖通過探索未標記數據來規范、調整決策邊界；直推式支持向量機（tranductive SVM，TSVM）[2]，它只考慮一個特定的測試數據集，試圖最小化這個測試集上的錯分率，而不考慮一般的情況，更強調直推式的概念；拉普拉斯支持向量機（Laplacian SVM）[15]，它將流行學習的方法引入到支持向量機中，有效利用了未標記樣本包含的知識等。

為了拓展關于半監督支持向量機方法的研究，本文提出了一種流形與成對約束聯合正則化半監督分類方法（semi-supervised classification method based on joint regularization of manifold and pairwise constraints，SSC-JRMPC），在流形正則化（manifold regularization，MR）[15]框架的基礎上引入了一項能夠有效利用監督信息的約束項，該約束項能夠讓人們在原有基礎上將數據標簽轉化為成對約束，從而可以進一步地利用已知的監督信息；同時流形正則化框架中的流形正則化項能夠保持樣本間局部幾何結構的特點，保留了流形學習方法在利用未標記樣本上的優勢。

2 相關工作

2.1 流形正則化框架

文獻[15]提出的流形正則化框架，將流形學習方法以及譜圖理論的知識引入到傳統的正則化方法中，主要是通過圖的拉普拉斯矩陣來探索數據的流形結構。假設有l個分屬于兩個不同的類(+1、-1)的標記樣本和u個未標記樣本組成的樣本集（前l個數據樣本為標記樣本）Xl+u={xi}(i=1,2,…,l,l+1,…,l+u)，它把標記的和未標記的數據編碼在一張鄰接圖中，圖的每一個節點代表一個數據點，如果兩個數據點之間有很大的相似性，就用一條邊將它們對應的節點連接起來。然后為未標記的數據找到合適的類別以使它們與標記的數據和潛在的圖結構的不一致性最小化。流形正則化單元為：

其中，邊權Wij表示樣本點之間的相似性；l、u分別為標記樣本數和未標記樣本數；；拉普拉斯圖L=D-W；D為權重矩陣W的對角度矩陣，。反映的是樣本分布的內在流形結構[14]。

將流形正則化單元引入到傳統的正則化方法，并結合再生核Hilbert空間（reproducing kernel Hilbert space，RKHS）[19]相關性質，就可以構造出流形正則化框架：

其中，V(xi,yi,f(xi))為損失函數，V(xi,yi,f(xi))=；y是樣本標簽，y∈{+1,-1}；正ii則單元用于控制分類器的復雜性，避免出現過擬合現象；是流形正則化項，用來保持樣本分布的內在流形結構。f(x)是決策函數，；γA、γI為兩個正則項的參數。

若損失函數V(xi,yi,f(xi))為支持向量機的合頁損失函數（hinge loss function），再結合再生核Hilbert的相關知識，可以得到由流形正則化框架衍生出的半監督支持向量機Laplacian SVM[15]的原始優化問題：

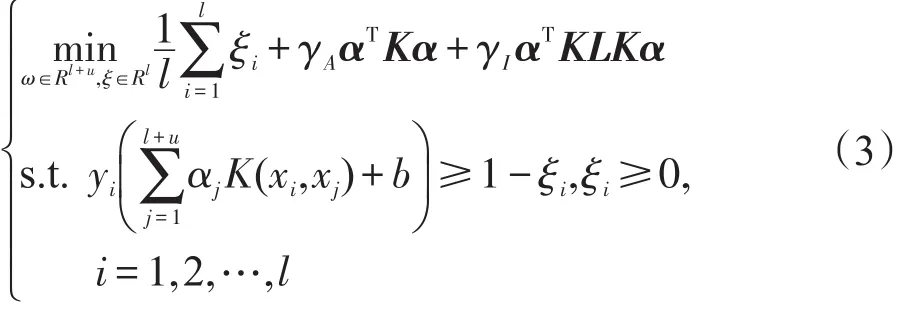
其中，l、u分別代表訓練樣本中標記樣本數和未標記樣本數；K(,)表示Mercer核函數；K是核矩陣，K=(Kij)l+u,l+u，Kij=K(xi,xj)；L是拉普拉斯圖矩陣。

根據Representer Theorems[19]，可以得到決策函數的相應形式：

2.2 成對約束監督信息的利用

一般而言，半監督學習中大多給定了部分數據標簽，一般做法是引入經驗風險項來加以利用，但不能忽略的是數據標簽可以轉換為成對約束這一信息類型。鑒于此，半監督算法中對監督信息的利用能夠通過將數據標簽轉換為成對約束來進一步利用監督信息。對于如何利用成對約束，一般的做法是將其構造成一個正則項，引入到原始優化問題中，具體的根據是在原始優化問題中當兩個有標記樣本xi、xj屬于同類時，可以判定W_mij=1，樣本對應的分類決策函數值f(xi)、f(xj)肯定是同號的，則這里(f(xi)-f(xj))的值就很小，優化問題中(f(xi)-f(xj))2W_mij就小；當樣本xi、xj屬于異類時，可以判定W_cij，樣本對應的分類決策函數值f(xi)、f(xj)肯定是異號的，即一正一負，f(xi)?f(xj)的值就小，優化問題中f(xi)f(xj)W_cij就小。必須關聯約束矩陣和不可能關聯矩陣的定義如下。

必須關聯約束矩陣W_m具體定義為：

式（5）中Lm為樣本中屬于同一類的組合數，i,j=1, 2,…,l,l+1,…,l+u；這里的其他情況包括樣本xi和xj中某一個標簽未知。

不可能關聯約束矩陣W_c具體定義為：

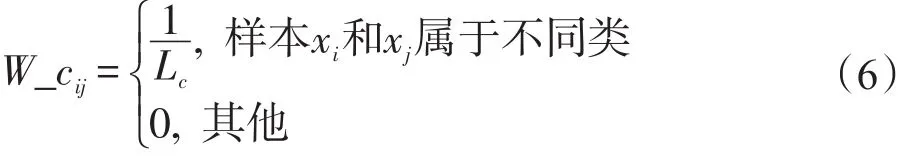
式

（6）中Lc為樣本中不屬于同一類的組合數個數；i,j=1,2,…,l,l+1,…,l+u；這里的其他情況包括樣本xi和xj中某一個標簽未知。

對于必須關聯約束的使用：

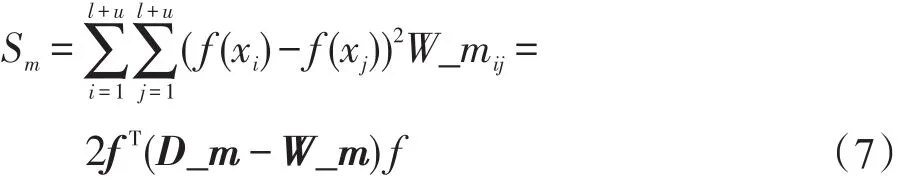
式（7）中f(x)是分類決策函數；W_m為必須關聯約束矩陣，為(l+u)階方陣；D_m為必須關聯約束矩陣W_m的對角矩陣，。

對于不可能關聯約束的使用：

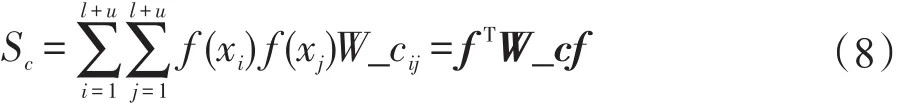
式（8）中f(x)是分類決策函數；W_c為不可能關聯矩陣，為l+u階方陣。需要說明的是雖然這里的關聯約束矩陣W_m和W_c都是l+u階方陣，但是這里得到的約束信息其實都是從一開始給定的有標記樣本中得到的，而必須關聯約束和不可能關聯約束信息除了可以從有標記樣本中得到，也有可能是包括那些雖然不知道樣本標簽，但知道哪些樣本屬同類，哪些屬異類。因此，保留矩陣大小為l+u階，而不是l階。

那么結合對兩種關聯約束的利用，可以得到對成對約束的利用，表示為：這里可以根據式（9）定義出監督約束矩陣Sw以及監督利用正則項S：

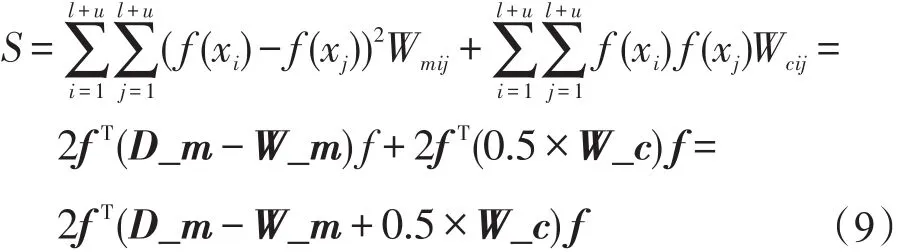
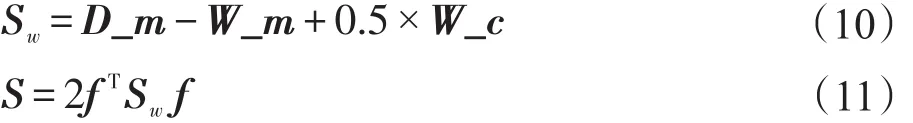
3 流形與成對約束聯合正則化半監督分類方法

前面介紹了拉普拉斯支持向量機的流形正則化框架、半監督學習中監督信息的類型及其利用，而本文的流形與成對約束聯合正則化半監督分類方法，從高效利用標記樣本等監督信息和有效學習未標記樣本知識兩個方面出發，提高分類器性能。假設有l個分屬于兩個不同的類(+1,-1）的標記樣本和u個未標記樣本組成的樣本集Xl+u={xi}(i=1,2,…,l,l+1,…,l+u)，這l個標記樣本中屬于同一類的組合數共Lm個，屬于不同類的組合數共Lc個。

把監督約束利用正則項S引入到流形正則化框架中，就可以得到SSC-JRMPC算法的目標函數：

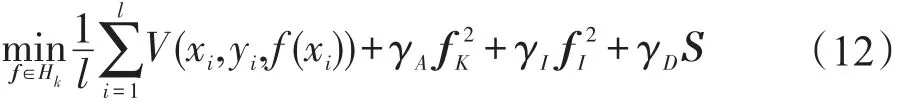
其中，V(xi,yi,f(xi))為標記樣本的損失函數，這里的損失函數選擇了與SVM相同的損失函數，即合頁損失函數，V(xi,yi,f(xi))=max{0,1-yif(xi)}=ξi，yi是樣本標記，yi∈{+1,-1}，ξi為松弛變量，表示訓練樣本集中標記樣本對應的ξi不為0，其余未標記訓練樣本點的ξ都等于0。f(x)是決策函數；正則單元用于控制分類器的復雜性，避免出現過擬合現象；是流形正則化項，用來保持樣本分布的內在流形結構；S是用來利用成對約束這種監督知識的正則項。γA、γI、γD作為3個正則項的參數，控制著各自對應正則項的復雜性。值得注意的是，當γD→0時，目標函數就退化為Laplacian SVM算法。

當樣本內在幾何結構呈現出非線性流形時，就要借助再生核希爾伯特空間的相關知識，利用核技巧把輸入空間(Rn)的數據映射到特征空間H（希爾伯特空間），再在特征空間里用線性分類學習方法從訓練數據中學習分類模型。

假設存在這樣的映射函數φ(x)：Rn→H，對所有的x,z∈Rn，Mercer核函數K(x,z)=φ(x)?φ(z)。根據對傳統SVM的了解，這里的分類決策面的法向量ω實際上是和所有訓練樣本（標記樣本和未標記樣本）都有關的，根據Representer Theorems[19]，可以將特征空間中的決策超平面法向量表示為：

4 實驗與結果分析

為了驗證本文SSC-JRMPC算法的有效性,將SSC-JRMPC算法分別在UCI數據集、文本分類數據集上進行測試，并與相應的方法進行比較。

4.1 實驗設置及運行環境

為了體現SSC-JRMPC算法的優勢，本文用了5種算法和SSC-JRMPC算法作比較，其中包括基礎的SVM算法和4個半監督方法，具體為TSVM、Laplacian SVM、meanS3VM-iter[15]、meanS3VM-mkl[15]。在實驗中有關參數選擇上，這里采用交叉驗證的方法，具體設置為當標記樣本點個數低于20個時，用留一法驗證；其他情況下用5折交叉驗證。對于對比算法meanS3VM-iter和meanS3VM-mkl，仍采用其原文獻推薦的參數區間設置；對于SVM算法，參數C尋優區間在{0.001,0.01,0.1,1,10,100,1 000}之間；本文SSCJRMPC算法和Laplacian SVM算法中的參數γA、γI、γD和近鄰點個數的尋優區間分別位于{10-5,10-4, 10-3,10-2,10-1,101,102}、{10-5,10-4,10-3,10-2,10-1,101,102}、[0:0.1:1]和{3,5,7,9}。所有算法均采用高斯徑向基核函數，核寬度參數σ2的取值為樣本數據的平均距離。同時，所有實驗僅提供了數據標簽這一種類型的監督信息。本文實驗均采用以下的硬件配置與編程環境：Windows 7系統，CPU是i5-4590，編程環境是Matlab 2013。

4.2 真實數據實驗及結果分析

4.2.1 UCI數據實驗及結果分析

為了更全面地說明本文SSC-JRMPC算法作為一種半監督分類方法具有的分類性能，UCI數據集具體參數如表1。同時，每個數據集的實驗中，都事先將源數據分割成一個訓練集和測試集，再在訓練集中取2%、4%、6%、8%、10%的點作為有標記樣本，余下作為未標記樣本參與半監督方法的訓練，這樣重復10次，取10次結果的均方差來進行統計。6種算法的實驗對比結果如圖1和表2所示。

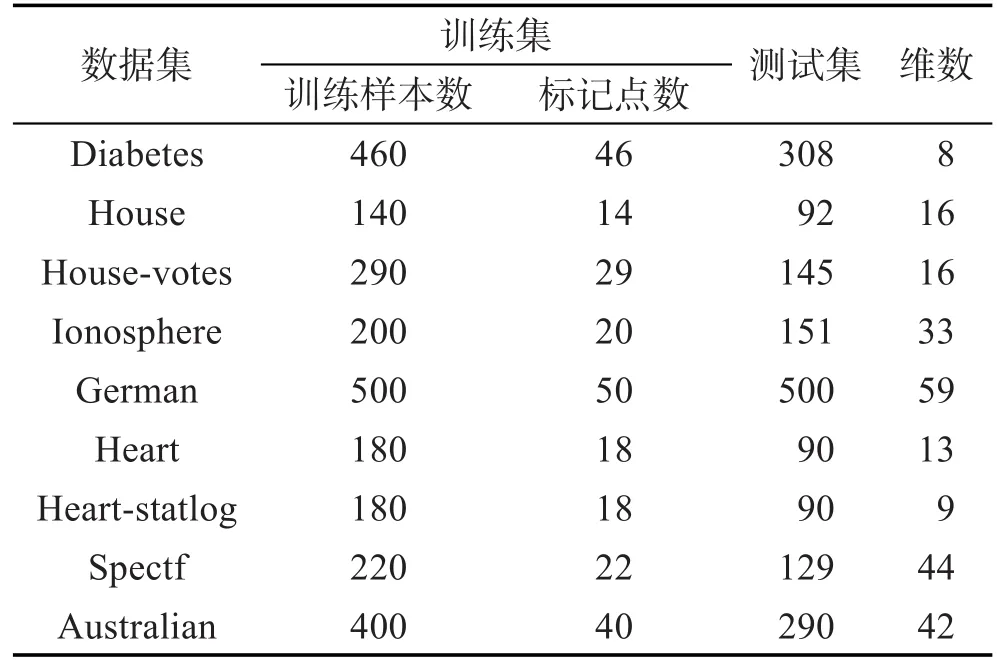
Table 1 UCI data parameters表1 UCI數據參數

觀察圖1和表2，可以得知如下結論：

首先，從圖1中可以看出，在標記樣本過少（2%、4%）的情況下，本文算法體現不了多大優勢。這主要因為SSC-JRMPC算法一部分是將標記樣本標簽轉化成關聯約束信息來利用，如果標記點過少，關聯約束信息的利用對算法影響甚微；只有當標記點足夠多時，關聯約束信息的利用才會對算法主體帶來較好效果。但無論如何，可以明顯地看出，本文SSCJRMPC算法都比Laplacian SVM算法要好，這也證明了本文算法結合充分利用標記樣本知識和有效學習未標記樣本知識這兩個方面的正確性和有效性。

其次，本文SSC-JRMPC算法比實驗中其他對比算法性能要好，歸根到底，可以理解為其他算法未能充分利用標記樣本知識和有效學習未標記樣本知識這兩個方面。SVM算法作為監督學習方法，只利用了標記樣本知識；Laplacian SVM雖然結合了兩個方面，但是并未充分完全利用到標記樣本知識，它主要依靠流形學習方法學習未標記樣本知識來達到訓練的目的；TSVM通過不斷迭代來達到最優，其實也只是依靠其中的標記樣本知識；meanS3VM方法中的兩個算法雖然結合了充分利用標記樣本知識和有效學習未標記樣本知識這兩個方面的知識，但是可以發現其利用標記樣本知識的策略和Laplacian SVM算法中一樣，并未充分完全地利用到標記樣本知識。

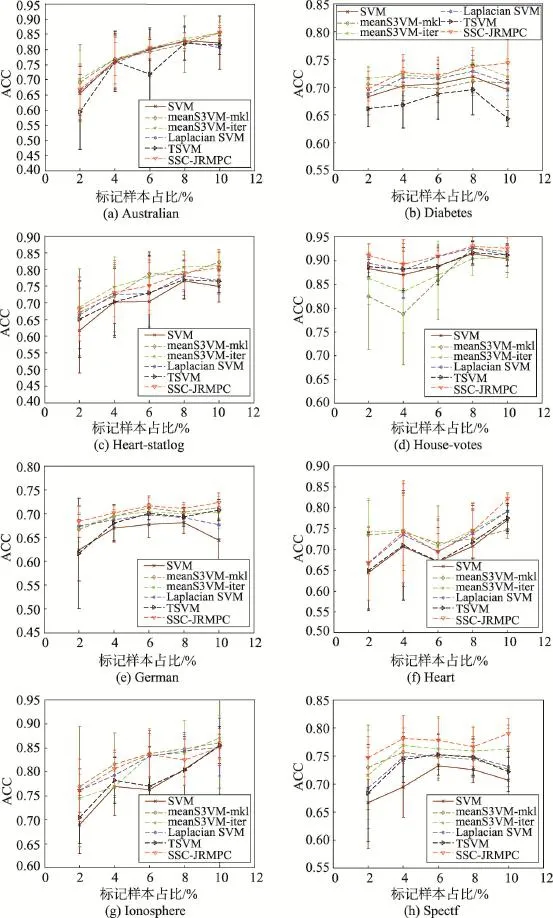
Fig.1 Classification performance comparison of 6 algorithms on different datasets圖1 不同數據集上6種算法分類性能比較

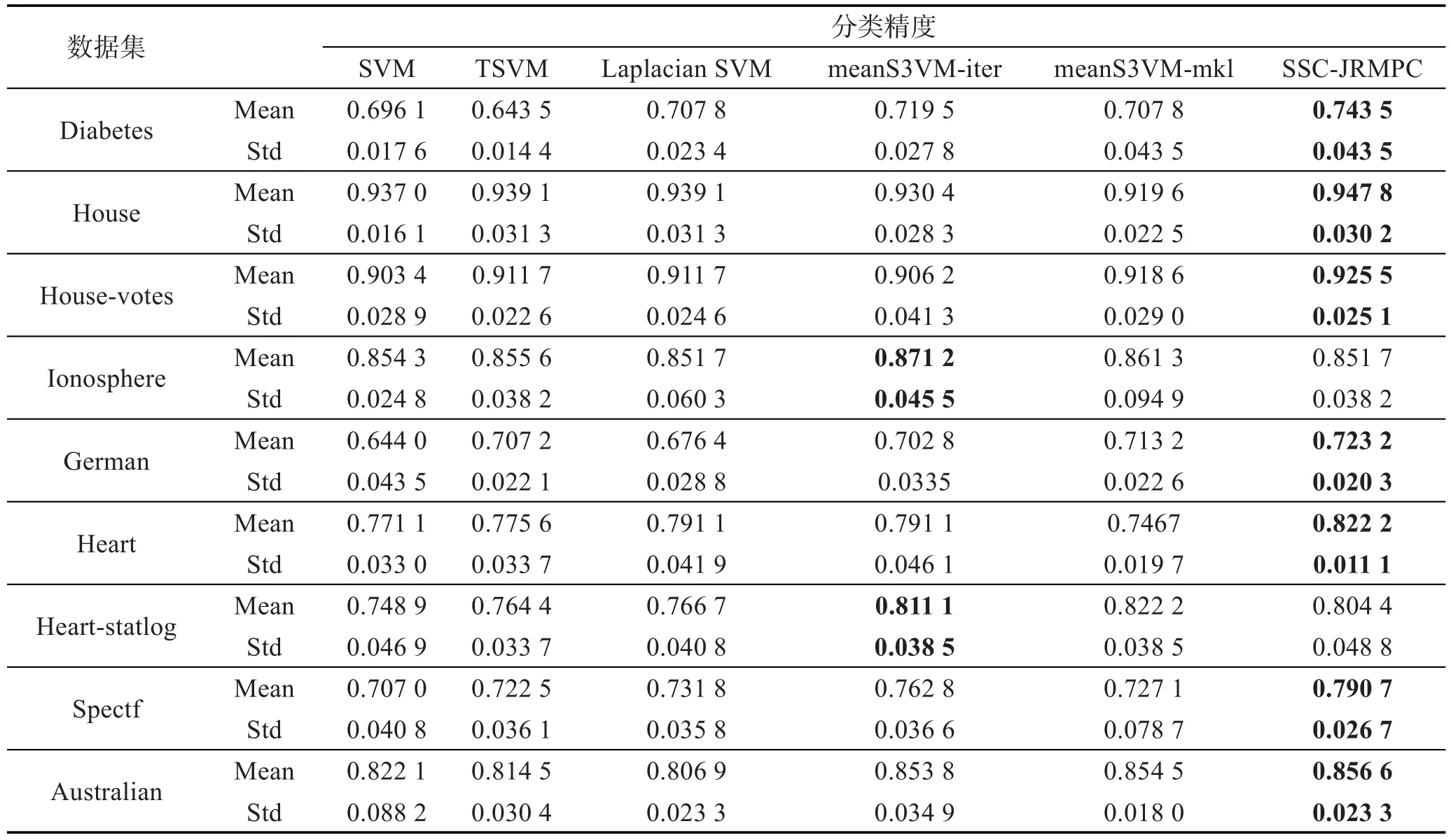
Table 2 Classification results of 6 algorithms on 10 percent labeled dataset表2 10%標記樣本點上6種算法分類結果

同時，在Heart-statlog和Ionosphere數據集中，雖然本文SSC-JRMPC算法效果稍次于meanS3VM-iter，但其算法效果依然不弱于其他算法。其原因可以歸結于，這里meanS3VM方法根據標記樣本的類別均值去估算未標記樣本均值，從而學習未標記樣本知識的作用要比流形學習的作用大；而且對標記樣本的利用已經很好，這點可以從SVM算法效果對比可以看出，因為它們利用標記樣本知識的策略相同，所以造成了meanS3VM方法分類效果稍好于本文算法。

4.2.2 文本分類實驗及結果分析

20個新聞組（20Newsgroups，20NG）[20]收集大約20 000篇新聞組文檔，涵蓋行政、體育等20個不同領域的新聞事件。20NG可分為4個大類，每個大類包含多個子類。特征上20NG很好地反映了不同文本數據集所具有的特征。這里對20NG中的4個大類兩兩組合來進行實驗，每個大類選擇500個樣本，并選取2個子類，具體數據構成見表3。實驗設置與UCI數據實驗相同。原始20NG數據維數很高，用BOW工具箱[21]對其進行了降維處理。實驗結果見表4。

觀察表4，可以得知如下結論：

本文SSC-JRMPC算法在TSVM算法處理文本分類問題稍顯優勢的情況下，依然表現出很好的效果，就算在“Comp VS talk”、“sci VS talk”實驗中，本文算法和TSVM表現的效果差距不大。原因可以總結為，TSVM方法最初就是針對文本分類問題提出來的，因此其在處理文本分類問題時優勢較明顯，但本文算法同時結合充分利用標記樣本知識和有效學習未標記樣本知識這兩個方面的知識，分類效果表現同樣很好，再次證明了本文SSC-JRMPC算法的正確性和有效性。

同時，可以看出SSC-JRMPC算法始終優于Laplacian SVM算法，原因可以歸結于SSC-JRMPC算法比Laplacian SVM算法能更為有效地利用標記樣本知識，通過參數調節其比重，保證了本文算法始終好于Laplacian SVM算法。

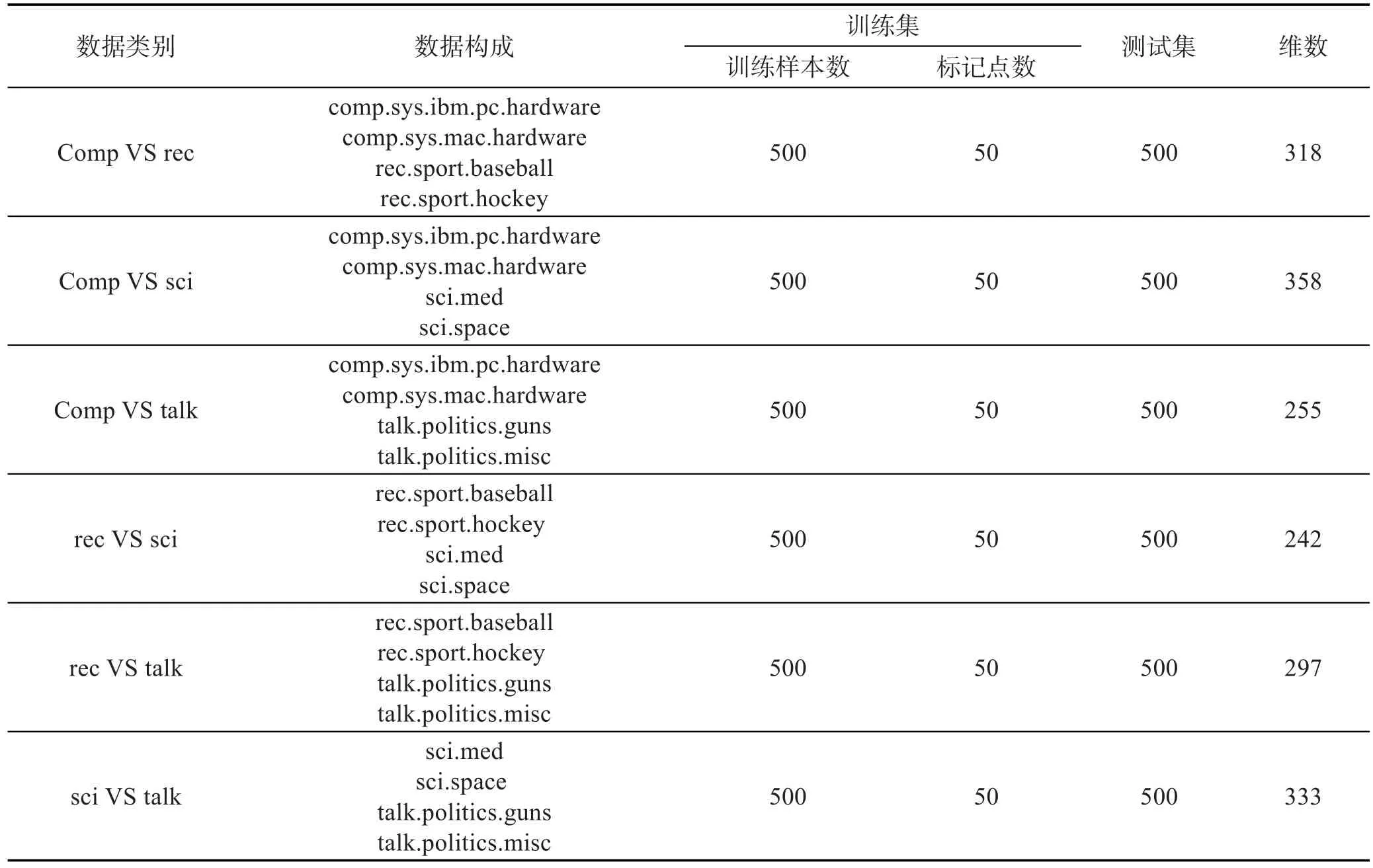
Table 3 Structure of text datasets表3 文本數據構成

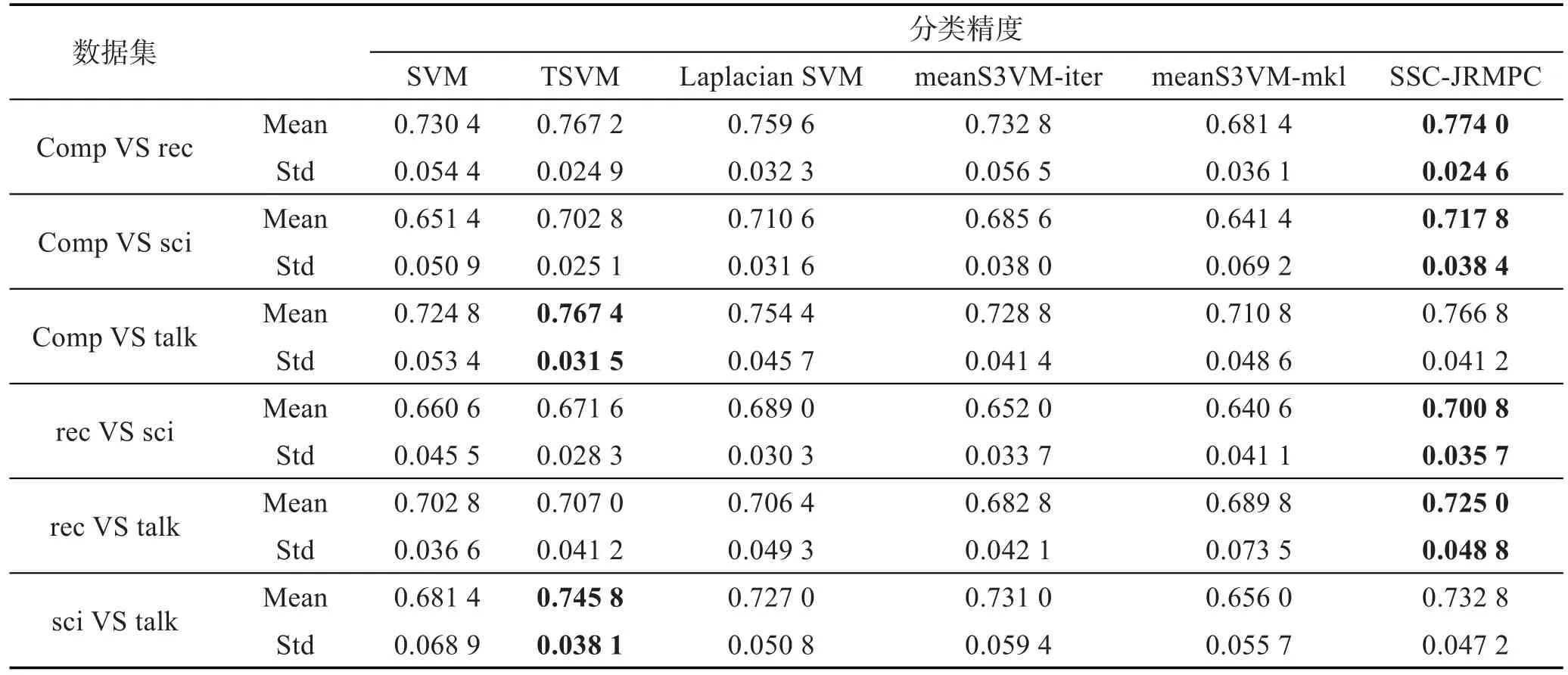
Table 4 Experimental results of text classification表4 文本分類實驗結果

5 結束語

本文歸納了半監督學習方法的一般特點，從充分利用標記樣本等監督信息知識和有效學習未標記樣本知識這兩個方面考慮來提高分類器性能，結合了流形框架的知識，提出了流形與成對約束聯合正則化半監督分類方法（SSC-JRMPC）。本文方法不但利用了流形學習方法有效利用未標記樣本的優勢，同時也考慮了如何進一步利用監督信息包含的知識。這些保證了SSC-JRMPC算法在對監督信息的利用上更具有一般適用性和有效性。由于監督信息約束正則項的引入，也會一定程度上提高算法的時間、空間復雜度，并且本文算法針對大型數據不具備快速學習能力，如何克服算法上述不足將是以后研究的方向。

[1]Gan Haitao.Research on semi-supervised clustering and classification algorithm[D].Wuhan:Huazhong University of Science and Technology,2014.

[2]Nigam K,McCallum A K,Thrun S,et al.Text classification from labeled and unlabeled documents using EM[J].Machine Learning,2000,39(2/3):103-134.

[3]Rosenberg C,Hebert M,Schneiderman H.Semi-supervised self-training of object detection models[C]//Proceedings of the 7th IEEE Workshop on Applications of Computer Vision, Breckenridge,USA,Jan 2005.Washington:IEEE Computer Society,2005:29-36.

[4]Bennett K,Demiriz A.Semi-supervised support vector machines[C]//Advances in Neural Information Processing Systems 11:NIPS Conference,Denver,Colorado,USA,Nov 30-Dec 5,1998.Cambridge,USA:MIT Press,1999:368-374.

[5]Fung G,Mangasarian O L.Semi-supervised support vector machines for unlabeled data classification[J].Optimization Methods and Software,2001,15:29-44.

[6]Chaudhari N S,Tiwari A,Thomas J.Performance evaluation of SVM based semi-supervised classification algorithm [C]//Proceedings of the 10th International Conference on Control,Automation,Robotics and Vision,Hanoi,Vietnam, Dec 2008.Piscataway,USA:IEEE,2008:1942-1947.

[7]Tang F,Brennan S,Zhao Q,et al.Co-tracking using semisupervised support vector machines[C]//Proceedings of the 11th IEEE International Conference on Computer Vision, Rio de Janeiro,Brazil,Oct 2007.Piscataway,USA:IEEE, 2007:1-8.

[8]Guillaumin M,Verbeek J,Schmid C.Multimodal semi-supervised learning for image classification[C]//Proceedings of the 23rd IEEE Conference on Computer Vision and Pattern Recognition,San Francisco,USA,2010.Piscataway,USA: IEEE,2010:902-909.

[9]Gao Jun,Wang Shitong,Deng Zhaohong.Global and local preserving based semi-supervised support vector machine[J]. Acta Electronica Sinica,2010,38(7):1626-1633.

[10]De Melo F M,De Carvalho F D A T.Semi-supervised fuzzy C-medoids clustering algorithm with multiple prototype representation[C]//Proceedings of the 2013 IEEE International Conference on Fuzzy Systems,Hyderabad,India, Jul 7-10,2013.Piscataway,USA:IEEE,2013:1-7.

[11]Zhao Jinguo,Chen Min,Zhang Zhao,et al.Localized pairwise constraint proximal support vector machine[C]//Proceedings of the 9th IEEE International Conference on Cognitive Informatics,Beijing,Jul 7-9,2010.Piscataway,USA: IEEE,2010:908-913.

[12]Zhang Zhao,Ye Ning.Constraint projections for discriminative support vector machines[C]//Proceedings of the 2009 International Joint Conference on Bioinformatics,Systems Biology and Intelligent Computing,Shanghai,Aug 3-5,2009. Washington:IEEE Computer Society,2009:501-507.

[13]Vapnik V N.Statistical learning theory[M].New York:Wiley Press,1998.

[14]Li Yufeng,Kwok J T,Zhou Zhihua.Semi-supervised learning using label mean[C]//Proceedings of the 26th Annual International Conference on Machine Learning,Montreal,Canada,2009.New York:ACM,2009:633-640.

[15]Belkin M,Niyogi P,Sindhwani V.Manifold regularization: a geometric framework for learning from examples[J].Journal of Machine Learning Research,2006,7:2399-2434.

[16]Zhao Ying.Research on semi-supervised support vector machines algorithms[D].Harbin:Harbin Engineering University, 2010.

[17]Li Yufeng,Kwok J T,Zhou Zhihua.Cost-sensitive semisupervised support vector machine[C]//Proceedings of the 24th AAAI Conference on Artificial Intelligence,Atlanta, USA,Jul 11-15,2010.Menlo Park,USA:AAAI,2010:500. [18]Li Yufeng,Tsang I,Kwok J T,et al.Convex and scalable weakly labeled SVMs[J].Journal of Machine Learning Research,2013,14:2151-2188.

[19]Sch?lkopf B,Herbrich R,Smola A J.A generalized repre-senter theorem[M]//Computational Learning Theory.Berlin,Heidelberg:Springer,2001:416-426.

[20]Dai Wenyuan,Xue Guirong,Yang Qiang,et al.Co-clustering based classification for out-of-domain documents[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Jose, USA,Aug 12-15,2007.New York:ACM,2007:210-219.

[21]McCallum A K.BOW:a toolkit for statistical language modeling,text retrieval,classification and clustering[EB/OL]. (1996)[2015-08-18].http://www.cs.cmu.edu/mccallum/bow.

附中文參考文獻：

[1]甘海濤.半監督聚類與分類算法研究[D].武漢:華中科技大學,2014.

[9]皋軍,王士同,鄧趙紅.基于全局和局部保持的半監督支持向量機[J].電子學報,2010,38(7):1626-1633.

[16]趙瑩.半監督支持向量機學習算法研究[D].哈爾濱:哈爾濱工程大學,2010.

XI Chen was born in 1993.He is an M.S.candidate at School of Digital Media,Jiangnan University.His research interests include pattern recognition,intelligent computation and its applications,etc.

奚臣（1993—），江南大學數字媒體學院碩士研究生，主要研究領域為模式識別，智能計算及應用等。

QIAN Pengjiang was born in 1979.He received the Ph.D.degree from Jiangnan University.Now he is an associate professor and M.S.supervisor at School of Digital Media,Jiangnan University.His research interests include pattern recognition and their applications,bioinformatics and medical image processing,etc.

錢鵬江（1979—），博士，江南大學數字媒體學院副教授、碩士生導師，主要研究領域為模式識別及應用，生物信息，醫學圖像處理等。

GU Xiaoqing was born in 1981.She is a Ph.D.candidate at School of Digital Media,Jiangnan University.Her research interests include pattern recognition,intelligent computation and its applications,etc.

顧曉清（1981—），女，江南大學數字媒體學院博士研究生，主要研究領域為模式識別，智能計算及應用等。

JIANG Yizhang was born in 1988.He is a Ph.D.candidate at School of Digital Media,Jiangnan University.His research interests include pattern recognition,intelligent computation and its applications,etc.

蔣亦樟（1988—），男，江南大學數字媒體學院博士研究生，主要研究領域為模式識別，智能計算及應用等。

Semi-Supervised Classification Method Based on Joint Regularization of Manifold and Pairwise Constraints*

XI Chen+,QIAN Pengjiang,GU Xiaoqing,JIANG Yizhang
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:xichen_0305@163.com

In order to improve the learning performance,semi-supervised learning methods aim at exploiting the knowledge of a small amount of labeled examples as well as lots of unlabeled data instances simultaneously.However, most existing semi-supervised approaches,primarily focus on the effective utilization of those label-unknown data, and the successive study regarding the label-known examples is usually neglected.In light of such situation,in terms of the manifold regularization framework,this paper proposes a novel semi-supervised classification method based on joint regularization of manifold and pairwise constraints(SSC-JRMPC).This method proceeds from two aspects:on one hand,inheriting from the manifold regularization framework,the optimization regarding both empirical risk and structural risk,and the use of intrinsic data distribution of entire dataset are considered concurrently;on the other hand, by transforming the sample labels into the must-link/cannot-link pairwise constraint conditions and incorporating these extended knowledge into own objective formulation,the knowledge existing in the supervision information is further mined.As the results,the classification accuracy of SSC-JRMPC is distinctly enhanced.The experiments on real-world datasets confirm the merits of this paper work.

semi-supervised learning;classification;manifold regularization;pairwise constraints

10.3778/j.issn.1673-9418.1510018

A

TP181

*The National Natural Science Foundation of China under Grant No.61202311(國家自然科學基金);the Natural Science Foundation of Jiangsu Province under Grant No.BK201221834(江蘇省自然科學基金);the R&D Frontier Program of Jiangsu Province under Grant No.BY2013015-02(江蘇省產學研前瞻性研究項目).

Received 2015-10,Accepted 2016-02.

CNKI網絡優先出版:2016-02-03,http://www.cnki.net/kcms/detail/11.5602.TP.20160203.1126.004.html

XI Chen,QIAN Pengjiang,GU Xiaoqing,et al.Semi-supervised classification method based on joint regularization of manifold and pairwise constraints.Journal of Frontiers of Computer Science and Technology,2017, 11(2)：303-313.