基于拉蓋爾函數的電子節氣門模型預測控制研究*
秦洋洋吳光強,2郭曉曉
(1.同濟大學,上海 201804;2.東京大學,生產技術研究所,東京 153-8505)
基于拉蓋爾函數的電子節氣門模型預測控制研究*
秦洋洋1吳光強1,2郭曉曉1
(1.同濟大學,上海 201804;2.東京大學,生產技術研究所,東京 153-8505)
建立面向電子節氣門控制器設計的線性模型,并在模型預測控制框架下設計了包含狀態變化和控制量變化的增廣狀態空間模型。在滿足電子節氣門的系統約束條件下,利用拉蓋爾函數特性,對控制量進行拉蓋爾多項式近似轉化,從而消除控制時域,降低算法復雜性。仿真試驗表明,基于拉蓋爾多項式的模型預測控制方法能夠實現電子節氣門的跟蹤控制,并降低系統計算量。
1 前言
電子節氣門是汽車發動機的重要控制部件,其控制系統基本目標是節氣門開度能夠快速精確且超調盡可能小地到達期望目標位置,節氣門開度的精確控制可以提高燃油經濟性,減少排放,迅速的系統響應,可獲得滿意的操控性能。因此,節氣門的控制對汽車的行駛安全性、動力性、平穩性及經濟性具有重要影響。
電子節氣門通過傳感器、控制器和驅動裝置實現加速踏板和節氣門之間的連接,替代了傳統的機械式連接。為了滿足節氣門的控制要求,文獻中提出了許多控制方法,主要包括模糊PID控制[1]、神經網絡控制[2~3]、滑模控制[4~5]、反步法控制[6~7]、輸出反饋控制[8]、時間最優控制等[9]。由于排放法規的日益嚴格和人們對車輛舒適性、動力性的期望越來越高,因此進一步研究提高電子節氣門控制性能的控制方法是很有必要的。
本文針對電子節氣門的控制要求,建立面向模型預測控制設計的電子節氣門線性離散模型,針對傳統模型預測控制系統在線求解精度與速度矛盾問題,采用拉蓋爾函數近似控制信號以降低在線優化復雜度。
2 預測模型設計
2.1 電子節氣門系統模型
模型預測控制是基于模型的控制算法,因此需要建立電子節氣門的數學模型,以進行模型預測控制器的設計。電子節氣門主要由驅動電機、減速齒輪組、復位彈簧、節氣門體及節氣門開度傳感器[10]組成,其結構如圖1所示。
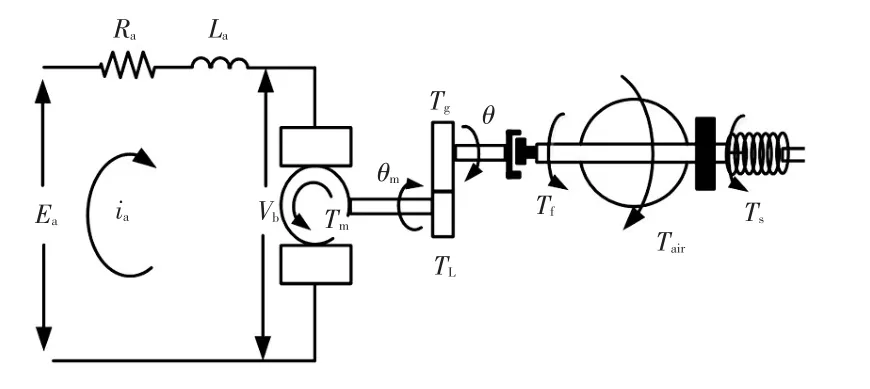
圖1 電子節氣門結構示意
根據基爾霍夫定律、電磁感應定律、磁場對載流線圈的作用定律可得節氣門電機的電樞電路[1]方程為:

式中,Ra和ia分別為電機的電阻和電流;La為電機電感;Vb和kb分別為電機的反電動勢和反電動勢常數;Ea為電機輸入電壓;θm為電機旋轉角度;Tm為電機轉矩;kt為轉矩常數。
式(1)經數學運算,并且考慮到電機的電感很小,可忽略不計,即La=0,則有:

忽略齒輪間隙的影響,則節氣門轉角θ與電機轉角θm之間的轉換關系為:

式中,n是減速齒輪組傳動比。
由式(2)和式(3)可得電機轉矩表達式:

根據廣義牛頓定律,忽略負載扭矩、庫倫摩擦及其它非線性因素,可得節氣門的運動學方程:

式中,J是折算后系統總的等效轉動慣量;Tsp為復位彈簧扭矩;Td為摩擦扭矩。

式中,ksp是復位彈簧系數,kd是粘性摩擦系數。

2.2 增廣狀態空間模型設計
由前文可知,電子節氣門系統實際為一單輸入單輸出系統,其輸入輸出離散傳遞函數標準形式可設為:

引入積分環節以消除靜態誤差[11],選擇增廣狀態變量:
則系統增廣狀態空間模型為:

3 預測模型拉蓋爾函數轉化
傳統模型預測控制算法是對式(9)所示系統,根據相應性能指標函數,轉化成以控制量為優化變量的二次規劃求解過程,文獻[12]指出,預測時域和控制時域越大,所求解出的控制結果越精確,然而由于模型預測控制算法具有在線優化的特點,其控制時域及預測時域并不能過大,否則系統實時性將迅速降低,因此利用拉蓋爾函數特性對控制量進行近似轉化,從而取消控制時域,以降低算法復雜性。
對拉蓋爾函數性質分析,n階離散拉蓋爾函數滿足[13]:

式中,0≤a<1是比例因子。
對離散拉蓋爾函數進行逆Z變換,得:

ln(m)滿足:

則控制信號變化量可用拉蓋爾函數近似表示[14],隨著多項式項數增加,式(13)多項式收斂于實際控制信號變化量。

式中,N為多項式展開項數;是采樣k時刻的系數函數;
對于式(9)所示系統,其預測模型可轉化為:
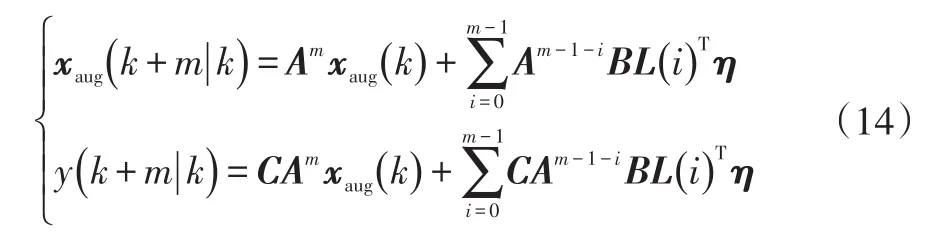

4 模型預測控制求解
4.1 控制目標函數分析
設系統性能指標函數:

由式(13)可知:

l()m在時域內同樣滿足正交性,即:

因此,式(15)性能指標函數等價于:


式中,Q=CTC。

代入式(19)可得:

忽略與優化變量無關的常數項,則算法求解轉化為在每次預測時間域里的二次規劃問題求解預測控制序列。
4.2 系統控制要求及約束處理
電子節氣門的具體量化控制要求為[6]:上升時間應不超過100 ms,調節穩定時間小于40 ms,即電子節氣門從上升到達穩態的總時間不大140 ms,控制器應使節氣門擋板不碰撞限位,即要求零超調,同時要求穩態誤差在±2%內。
由于電子節氣門驅動電機的飽和限制,電子節氣門系統輸入電壓必須限制在-12~+12 V,且電壓變化速率不能過大以確保控制動作的平順性,即控制器必須滿足以下約束條件:

對以上約束條件,轉化成矩陣形式:

因此,在MPC的框架下,電子節氣門系統控制策略設計最終轉化為式(24)帶約束的在線二次優化問題。

求解式(24)可得預測控制時域下的控制序列,對于求出的控制序列,只選取其中第1個控制量作為當前控制器輸出,下一時刻基于當前系統狀態重新求解上述約束優化問題,實現在線滾動優化計算。
5 仿真分析
為了驗證所設計的節氣門位置跟蹤的線性模型預測控制器的功能和有效性,在MATLAB/Simulink中搭建節氣門的數學模型,并進行離線仿真試驗。節氣門系統的模型參數如表1所列。

表1 節氣門系統模型參數
控制系統中,a=0.7,N=4,rw=0.3,Np=46,采樣步長為1 ms,為驗證該算法可行性與優越性,采用傳統模型預測控制算法[15]作對比,控制時域Nc=4。
圖2~圖5所示為期望節氣門角度作幅值θd=1rad階躍變化的跟蹤響應,基于拉蓋爾函數模型預測控制算法(以下簡稱改進算法)與傳統模型預測控制算法(以下簡稱傳統方法)在響應、控制量、控制量增量及系統求解時間等方面的對比情況。

圖2 階躍信號系統響應

圖3 階躍信號控制量曲線

圖4 階躍信號控制量增量曲線

圖5 階躍信號系統求解時間曲線
由圖2可知,應用改進算法沒有超調,而傳統模型預測控制算法系統卻發生超調現象。改進算法能更快達到穩態,在40 ms左右穩定,而傳統模型預測控制算法在100 ms左右才達到穩定。由圖3和圖4可知,兩種算法都滿足約束條件,傳統模型預測控制算法控制量更平滑,但可以通過改變控制量速率的上下限來提升改進算法控制動作的平滑性。由圖5可知,改進算法求解時間相對傳統算法穩定,而傳統算法求解時間波動較大,這不利于實際控制系統設計,而兩者求解時間數值差別不大是因為傳統算法控制時域及預測時域不大,要取得和改進算法相同的效果,需要增加控制時域和預測時域,加長求解時間。
圖6~圖9所示為期望節氣門頻率1 Hz、幅值θd=1rad正弦信號時的跟蹤響應。
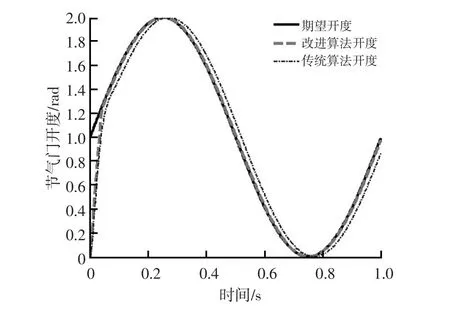
圖6 正弦信號系統響應

圖7 正弦信號控制量曲線

圖8 正弦信號控制量增量曲線
由圖6~圖9正弦信號系統響應對比進一步顯示改進算法的優越性,在動態響應方面(圖6),改進算法優于傳統模型預測控制算法,其正弦跟蹤響應誤差在2%以內,而傳統算法誤差較大;動態響應系統求解時間波動情況(圖9)方面,改進算法也優于傳統算法。

圖9 正弦信號系統求解時間曲線
6 結束語
建立節氣門系統模型,并設計包含狀態量變化及控制量變化的增廣狀態空間模型以使控制系統消除穩態誤差,針對傳統模型預測控制算法求解時間和控制精度矛盾問題,設計了基于拉蓋爾多項式近似的模型預測控制算法,取消了控制時域,改善了控制系統性能。仿真結果表明,所設計的控制算法能很好的滿足電子節氣門控制需求,且相較于傳統模型預測控制算法得到了改善。
1 Yang C.Model-Based Analysis and Tuning of Electronic Throttle Controllers.SAE Technical Paper,2004-01-0524: 8~11.
2 Baric M,Petrovic I,Peri N.Neural network based sliding mode controller for a class of linear systems with unmatched uncertainties.41st IEEE Conference on Decision and Con?trol,Las Vegas,2002:967~972.
3 毛六平,王耀南.基于模糊高斯基函數神經網絡的電子節氣門控制的仿真研究.電氣應用,2006,25(11):39~43.
4 Hashimoto E,Ishiguro T,Yasui Y,et al.High Reliability Electronic Throttle System Design.SAE Technical Paper, 2003-01-0708:1~9.
5 Dagci O H,Pan Y,Ozguner U.Sliding mode control of elec?tronic throttle valve.Proceedings of the American Control Conference,Washington D.C.,2002:1996~2001.
6 宋同好.基于Backstepping的電子節氣門控制:[學位論文].長春:吉林大學,2009.
7 陳虹,胡云峰,郭宏志,等.基于Backstepping方法的電子節氣門控制.控制理論與應用,2011,28(4):491~496.
8 胡云峰,李超,李俊,等.基于觀測器的輸出反饋電子節氣門控制器設計.自動化學報,2011,37(6):746~754.
9 Vasak M,Baotic M,Morari M,et al.Constrained optimal control of an electronic throttle.International Journal of Con?trol,2006,79(5):465~478.
10 朱二欣.電子節氣門控制系統的開發研究:[學位論文].長春:吉林大學,2005.
11 鄒濤,丁寶蒼,張端.模型預測控制工程應用導論.北京:化學工業出版社,2010.
12 Garcia C,Prett D,et al.Model predictive control:theory and practice-a survey.Automatica,1989,25(3):335~348.
13 Wahlberg B.System identification using Laguerre models.Automatic Control IEEE Transactions on,1991,36(5): 551~562.
14 Wang Liuping.Discrete model predictive controller design using Laguerre functions.Journal of Process Control,2004, 14(2):131~142.
15 許芳.快速模型預測控制的FPGA實現及其應用研究:[學位論文].長春:吉林大學,2014.
(責任編輯 晨 曦)
修改稿收到日期為2016年7月20日。
Model Predictive Control Study of Electronic Throttle Based on Laguerre Functions
Qin Yangyang1,Wu Guangqiang1,2,Guo Xiaoxiao1
(1.Tongji University,Shanghai 201804;2.Institute of Industrial Science,the University of Tokyo,Tokyo 153-8505)
To meet the needs of following control of electronic throttle and improve the efficiency of control algorithms,a linear model facing controller design has been built,meanwhile an augmented state space model including changes of state and controlled values on the basis of model predictive control has also been designed.On the restrictions of electronic throttle,controlled variable has been approximately converted using the characteristic of Laguerre functions, which can eliminate control horizon and reduce complexity of control algorithms.Besides,an optimal control sequence using model predictive control based on Laguerre functions was created,which in this way can not only guarantee the dynamic performance of following control,but also reduce the amount of calculation.The simulation showed that the approach of model predictive control using Laguerre functions can better fulfill the following control of electronic throttle and at the same time the calculation amount of the whole system has been decreased.
Laguerre functions,Electronic throttle,Model predictive control
拉蓋爾函數 電子節氣門 模型預測
U464.11+2
A
1000-3703(2017)01-0033-05
上海汽車工業科技發展基金會項目(1526)。

