聲學邊界元擬奇異積分計算的自適應方法
繆宇躍, 李天勻,3, 朱 翔, 張冠軍, 郭文杰
(1.華中科技大學 船舶與海洋工程學院, 武漢 430074; 2.船舶與海洋水動力湖北省重點實驗室, 武漢 430074;3.船舶振動噪聲重點實驗室, 武漢 430064)
聲學邊界元擬奇異積分計算的自適應方法
繆宇躍1,2, 李天勻1,2,3, 朱 翔1,2, 張冠軍1,2, 郭文杰1,2
(1.華中科技大學 船舶與海洋工程學院, 武漢 430074; 2.船舶與海洋水動力湖北省重點實驗室, 武漢 430074;3.船舶振動噪聲重點實驗室, 武漢 430064)
提出一種自適應方法計算聲學邊界元中的擬奇異積分,通過單元分級細分將總積分轉移到子單元上以消除擬奇異性。在此方法基礎上深入研究擬奇異性,進一步提出接近度的概念,其中臨界接近度可作為擬奇異積分計算的理論依據,并可用于預估擬奇異性是否存在。此方法的積分精度可調控,且不受場點位置限制,相比于已有方法更加靈活高效。數值分析表明擬奇異性強弱由場點與單元的相對位置決定,單元上遠離場點的區域擬奇異性很弱,無需處理。研究結果為處理邊界元法中的擬奇異性問題提供了新的選擇和參考。
邊界元;擬奇異性;自適應;接近度
聲學邊界元法經過幾十年的發展, 已經成為求解結構振動聲輻射問題的重要方法,得到了比有限元法更廣泛的應用,尤其與快速多極算法結合后[1],體現出較強的實用性。奇異積分問題[2,3]在邊界元法中由來已久,已有多種處理方法,隨后擬奇異積分問題也成為研究熱點。擬奇異性,又稱為近奇異性[4]或幾乎奇異性[5],是由于場點十分靠近結構表面,導致場點與源點間的距離很微小。雖然其物理機理不存在奇異性,但在數值計算時,這種微距使常規的高斯積分法失效,產生類似奇異性的收斂性差問題。
為處理邊界元法的擬奇異性,國內外研究者提出了多種方法。TANAKA等[6]提供了一個較詳實的關于擬奇異積分正則化方法的綜述文獻。ZHANG等[7]提出了一種半解析法,采用曲面單元,有效地處理了薄壁結構的擬奇異性。針對二維彈性問題,NIU等[8]提出一種解析的擬奇異積分算法,隨后這種方法被應用到二維的正交各向異性勢問題[9]和各向異性勢問題[10]中。對于三維勢問題,NIU等[11]將奇異性降階,并結合正則化方法能夠更容易地計算擬奇異積分。
自適應方法源自自動控制優化領域,并在有限元法中得到發展,隨后這種自適應的思想被引入邊界元法的研究中,但是主要被用來進行整體或局部的單元細分以提高計算精度[12],KITA等[13]對自適應邊界元法的發展應用做了較詳實的概括。根據自適應單元細分的特性,研究者開始將這種方法應用于擬奇異積分的計算中。WEI等[14]基于CFD理論,結合有限元和邊界元法分析了水下航行體噪聲,其中邊界元的奇異性問題采用自適應單元平均細分法處理。CROAKER等[15]對氣流中結構的誘導聲散射進行預報研究,為了得到近場壓力和壓力梯度,對擬奇異性體積分和面積分采用了單元細分法。DONG等[16]提出非穩態導熱問題的邊界元算法,為避免小時間步長的奇異性,采用坐標變換結合體單元細分法來提高域積分精度。DAVIES等[17]提出三維彈塑性邊界元法研究復雜的地質力學問題,將域積分變換為邊界積分消除強奇異性,并運用自適應細分法優化積分過程,其中單元細分過程依據經驗公式進行。GAO等[18]進一步將自適應單元細分法和解析法相結合計算多種類型的二維奇異積分并取得良好效果。LI等[19-22]同樣依據這種經驗公式進行單元細分來處理三維問題的擬奇異性,其中子單元尺寸以及子單元與源點距離需要通過反復迭代計算和誤差分析確定,而這種經驗公式未充分考慮場點與單元相對位置的不同所存在的差異。ZHANG等[23-24]利用邊界點法和邊界面法研究三維勢問題,擬奇異積分通過自適應單元細分實現,其細分準則是:比較每個子單元的對角線長度和近場點到該子單元中心的距離,若前者小于后者則認為細分達到積分要求,否則繼續進行細分以達到積分要求。依據這種“對角線準則”的自適應細分法能夠準確計算擬奇異積分,但若運用在聲學分析中則過于苛刻,增加不必要的計算量。
本文提出分級細分自適應方法,制定合理易行的細分方案,將多種情況下的擬奇異積分計算統一起來。在深入研究場點與單元不同的相對位置所存在差異的基礎上提出接近度的概念,為擬奇異積分計算提供理論基礎,并預估擬奇異性程度以確定是否需要處理擬奇異性。數值分析證明了這種自適應方法能夠很好的計算擬奇異積分,具有較好的靈活性和高效性,研究結果可為自適應邊界元法的發展提供思路和參考。
1 聲學邊界元法基本理論
對于自由空間的聲輻射問題,其Helmholtz邊界積分方程為:
C(z)p(z)=
(1)
將基本解中的指數項按Taylor級數展開:
(2)
并設:
(3)
則有:
(4)
(5)
(6)
可見基本解G的弱奇異性是由Gr引起的,Gr是與頻率無關的,而Gk是無奇異性的,可以進行高斯積分。
場點在S上時,對于平面單元,r⊥ns,故?r/?ns=0,則?G/?ns=?G/?r·?r/?ns=0,只存在弱奇異性。場點不在S上時,r⊥ns這個條件不成立,故?G/?ns≠0,則同時存在弱奇異性和強奇異性。實際上弱奇異積分比強奇異積分更容易收斂,所以只需保證強奇異積分收斂,便能消除積分方程的奇異性。
2 自適應細分方法
本文提出分級細分的自適應方法,并與其他自適應方法對比驗證精度和收斂性。由于二維高斯積分是通過等參變換建立各種不規則單元與規則四邊形單元的映射關系,之后在一個局部坐標系的正方形平面區域數值求解積分,所以文中統一采用頂點坐標為[-1, -1]、[1, -1]、[1, 1]和[-1, 1]的標準正方形單元來說明自適應細分方法,如圖1所示。下文中所有省略的長度單位都是米。圖1中黑點表示近場點在單元上的投影點,每行從左往右是自適應細分方案,第(1)行是平均細分方案,文獻[14]在處理奇異積分時便是采取這種方案;第(2)~(5)行是投影點在不同位置時的分級細分方案。
平均細分方法是將原始單元平均細分為四個子單元,在下一次細分過程中每個子單元再平均細分為四個更小的子單元,如此遞推下去將原始單元上的積分轉移到各個子單元上去,直到全部子單元積分總和的誤差達到收斂容許值為止。
分級細分方法是圍繞近場點在單元上的投影點來細分,對原始單元進行平均細分后,只將投影點所在的子單元再次平均細分,其他子單元不變,如此下去直到收斂。由于投影點位置不同,于是產生了(2)~(5)這幾種分級細分方案。
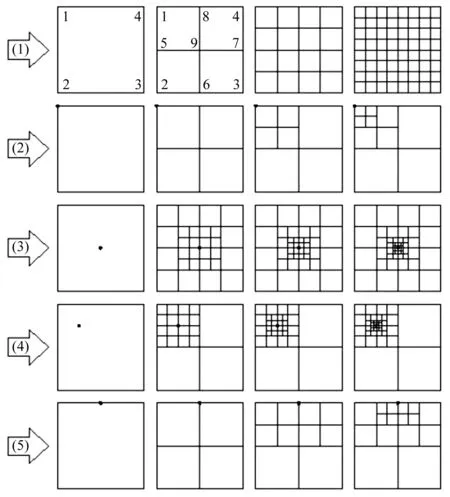
圖1 自適應細分方案Fig.1. The adaptive subdivision processes
細分后,原始單元上的弱奇異積分和強奇異積分就變為子單元上的積分總和:
(7)
(8)
式中:s為原始單元,sj為子單元,N為子單元總數,Ng為高斯點數,Jj為子單元Jacobian,wu和wv為權系數。
設num為細分次數和子單元級別,則圖1中五種細分方案的子單元總數為
(9)
由于平面單元的X、Y和Z坐標都是線性變化的,以X坐標為例說明如何根據自適應算法得到子單元坐標。對于平均細分方案,如圖1中的第(1)行, 第一級子單元與原始單元的坐標關系如下:
(10)
其中T1~T4是坐標傳遞矩陣,X0是原始單元坐標:
(11)
于是通過同樣的坐標傳遞,第二級子單元坐標為
(12)
如此繼續下去,細分num次獲得的所有子單元坐標為
(13)
式中:m1=1~4,m2=1~4。
對于分級細分方案,如圖1中第(2)行,只對投影點所在單元進行平均細分,每次細分產生三個不含投影點的子單元,最后剩下一個投影點所在單元,故第num級子單元坐標為
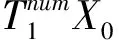
(14)
圖1中第(3)~(5)行的分級細分方案具有很高相似性,其子單元坐標的自適應算法都可參照第(2)行。由此便可清晰地構建各種情況下的自適應細分方法,不需要迭代和判斷,只需要設定細分次數。
3 近場點的接近度
在進行收斂性分析之前,先要提出接近度的概念,并根據接近度決定單元劃分的次數。由于近場點與單元的相對位置并不固定,不同的接近程度對擬奇異性的影響是有差別的。文獻[25]初步指出擬奇異性是近場點與高斯積分點相互作用的結果,接近高斯點的區域會產生較強的奇異性,其他區域則很弱。為了深入發掘接近度對擬奇異性的影響,本文在標準單元周圍取了若干近場點進行研究,如圖2所示。由于正方形的對稱性,只在八分之一直角三角形OAB附近取十個近場點,采用十點高斯積分,①~⑥號點投影在OAB的邊上,⑦~⑩號點在平面OAB上,坐標如表1所示,其中t為場點到單元的距離。使每一近場點沿直線不斷接近單元并考察收斂性:若頻率無關的強奇異積分∫s-1/r2·?r/?nsds在三次細分以內收斂并且不細分的積分值與細分收斂后的積分值相對誤差不超過1%,那么此時的距離稱為“近遠場”的臨界值,超過這個臨界距離就不存在擬奇異性,場點不再是近場點,單元也不需要細分就可正常積分。本文定義這種場點到單元的距離t與單元邊長l的比值稱為近場點的接近度E,即E=t/l。通過逼近計算得到場點到單元的臨界距離t0和臨界接近度E0如表2所示,其中⑦~⑩號點的?r/?ns=0,故這些點的強奇異積分以∫s-1/r2ds表示。
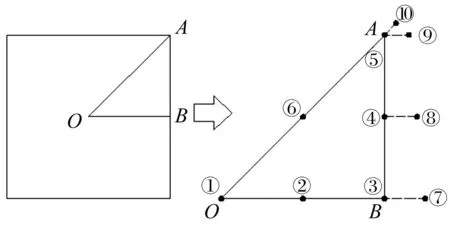
圖2 近場點與標準單元的相對位置Fig.2 The relative positions of near-field points to the standard element
從表2看出①~⑥號點和⑦~⑩號點的臨界距離t0和臨界接近度E0各不相同,明顯呈現出隨著與O點距離增大而減小的趨勢,表明場點離高斯積分區域越遠,相互作用越弱,擬奇異性程度越低。
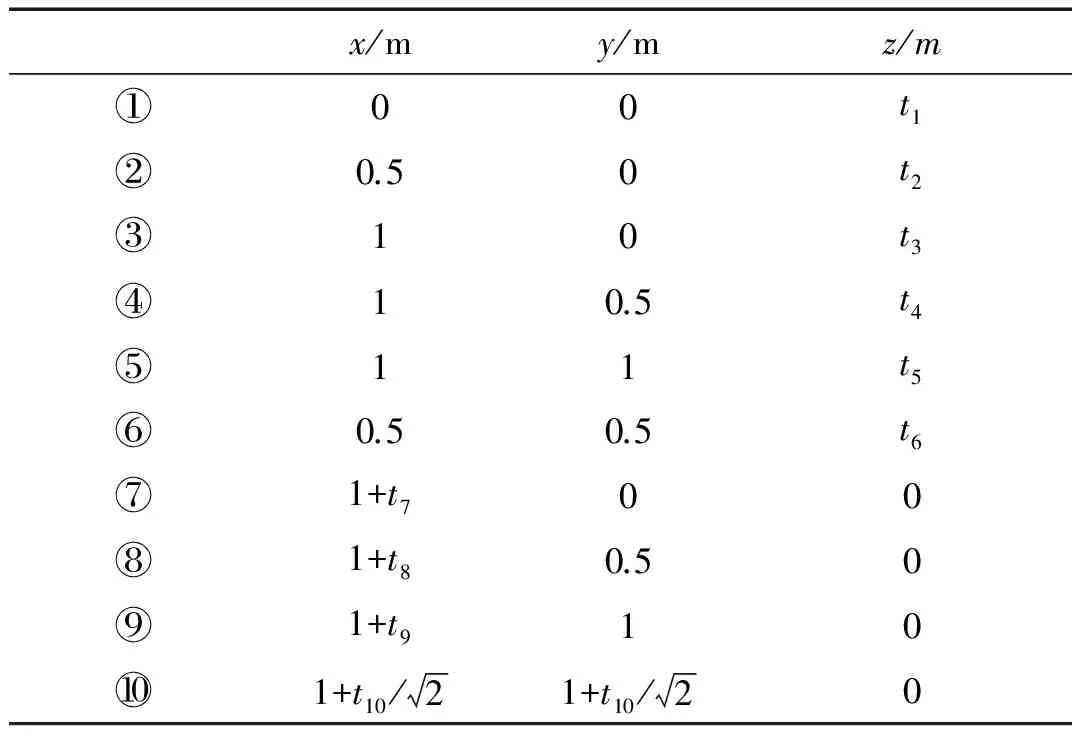
表1 近場點坐標
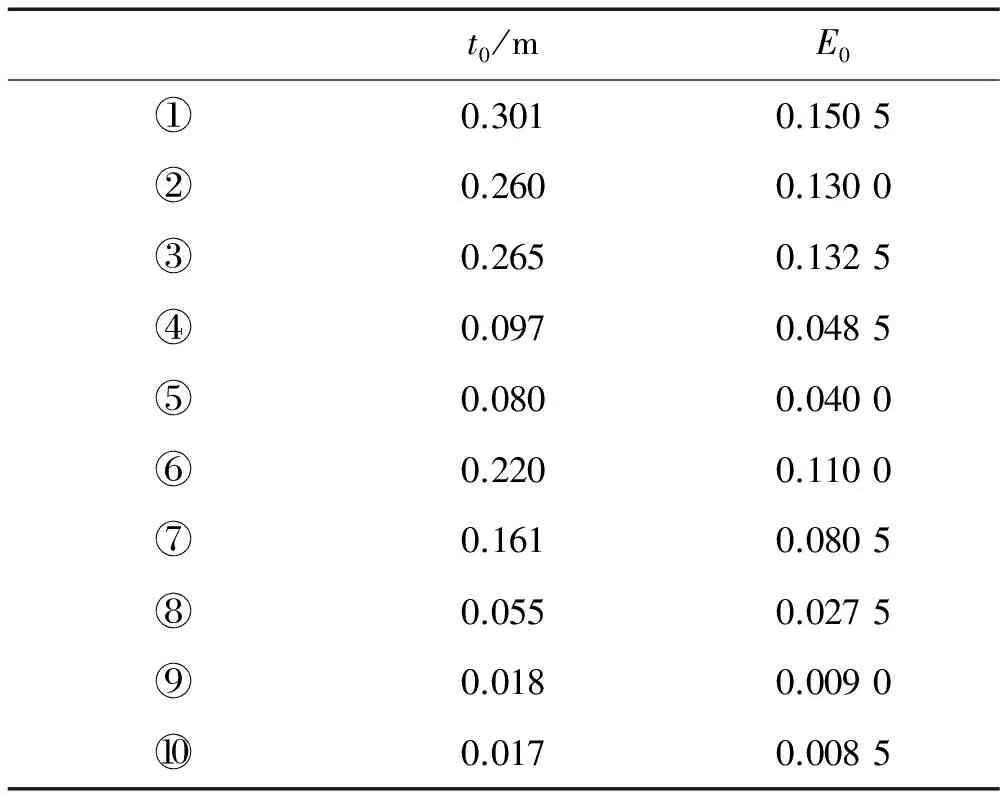
表2 臨界距離和臨界接近度
文獻[17-22]采用的經驗公式為
(15)
式中:A1為近場點到積分單元最小距離,A2為單元在積分方向上的長度,A3為該積分方向上的高斯點數,A4為奇異性階次,A5為該積分方向上的高斯積分誤差。對于標準單元取A2=2,A3=10,A4=2,A5=0.01,計算得到臨界距離為A1=0.168 6,并不能滿足任意位置近場點的誤差要求,未體現出相對位置變化所帶來的差異。
由于分級細分方法是圍繞近場點在單元上的投影點來細分,實際造成場點與最小子單元的位置關系等同于⑤號點與標準單元的位置關系,所以采用十點高斯積分并且誤差閾值為1%時,分級細分次數num可根據接近度(場點到單元距離與最小子單元邊長之比)來決定,即t/(l/2num)≥0.04,于是得到:
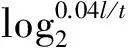
(16)
式中l為原始單元平均邊長。式(16)可作為擬奇異積分的單元細分準則。
4 收斂性分析
首先以標準單元(l=2)的收斂性分析驗證分級自適應方法和單元細分準則的正確性。采用十點高斯積分,k=1 rad/m,取四個場點(編號1~4),坐標分別為[0, 0, 0.01]、[1, 1, 0.01]、[0, 0, 0.001]和[1, 1, 0.001],四個場點對應的強奇異積分分別表示為IR1、IR2、IR3和IR4,每次細分的積分值與最終收斂值的誤差分別表示為er1、er2、er3和er4,收斂性曲線如圖3所示。
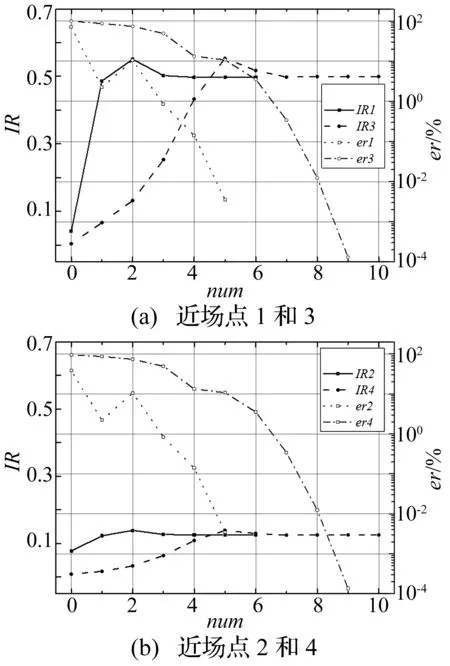
圖3 標準單元的積分收斂性曲線Fig.3 The convergence curves for the standard element
圖3中只展示了IR實部,因為IR虛部幾乎沒有變化,可見強奇異性由積分的實部來體現,而弱奇異積分收斂非常快,同樣不予展示。通過誤差曲線er1和er2看出經過3次以上細分,誤差就能降到1%以下,而誤差曲線er3和er4顯示經過7次以上細分,誤差也降到1%以下。可見對于t分別為0.01和0.001的場點,收斂情況完全符合式(16)的細分準則。
若按照式(15)計算得到離場點最近子單元長度分別為0.118 6和0.011 9,需要細分5次和8次;若按照文獻[23-24]中的“對角線準則”計算得到離場點最近子單元長度分別為0.008 2和0.000 82,需要細分8次和12次,都增加了額外的計算量。另外,式(15)和“對角線準則”需要考察每個子單元是否滿足要求,單元的細分是一種反復迭代判斷過程,而根據本文的單元細分依據式(16)可以進行預判,然后按本文的自適應方法一次性劃分子單元和計算坐標,更加簡捷實用。
再以寬為2,長分別4和8的兩種矩形單元(分別簡稱為“矩四”和“矩八”)進行驗證。令t=0.01,近場點5和6分別投影于“矩四”的中心和頂點;近場點7和8分別投影于“矩八”的中心和頂點。相應的奇異積分分別表示為IR5~8,每次細分的積分值與最終收斂值的誤差分別表示為er5~8,收斂性曲線如圖4所示。
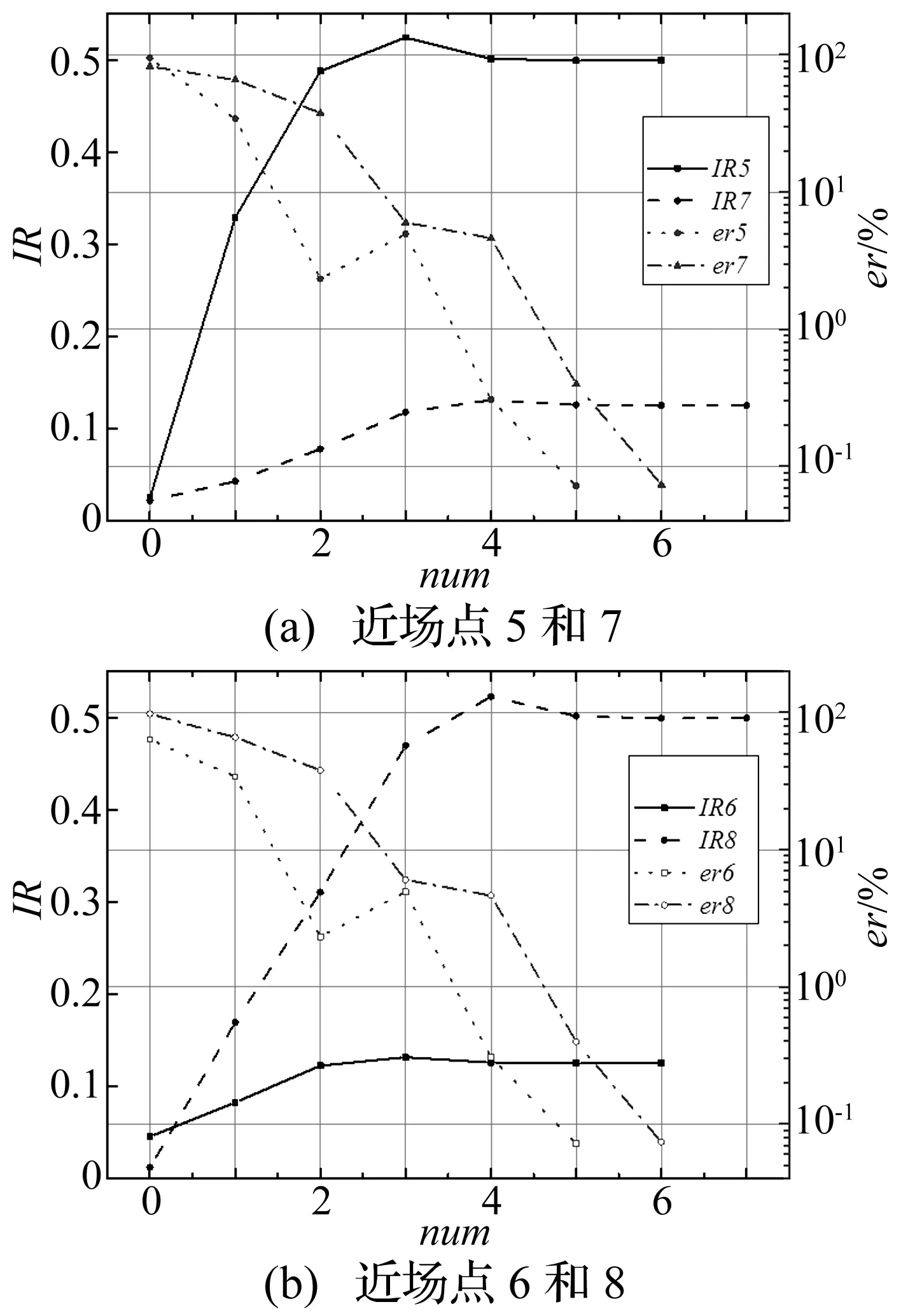
圖4 矩形單元的積分收斂性曲線Fig.4 The convergence curves for the rectangular elements
圖4顯示對于t為0.01的場點,分別經過4次和5次以上細分,誤差也降到1%以下,收斂情況同樣完全符合式(16)的細分要求。若按照式(15)的要求,需要細分6次和9次;若按照“對角線準則”,需要細分11次和13次,這樣也增加了額外計算量。
值得注意的是,采用分級細分方法和平均細分方法得到的計算結果并無差別,這充分說明了分級細分方法的準確性,同時也表明單元上不同區域對擬奇異性的影響不同:越靠近場點的區域對奇異性的貢獻越大,而遠離節點的區域對奇異性的貢獻迅速減小。常規高斯積分未考慮這種差別導致積分不準,平均細分方法平均化處理整個單元會增加很多不必要得計算量,而分級細分方法梯度化地對待遠近區域,符合奇異性產生的物理本質,既保證了精度也節省了計算量。根據式(9),兩種細分方法產生的子單元總數如表3所示。

表3 兩種細分方法產生的子單元總數
由以上積分收斂性分析可見,自適應分級細分方法能克服弱奇異性和強奇異性,有效計算擬奇異積分。同時依據本文所提的細分準則能夠準確預判,不需要反復迭代判斷,產生子單元數量更少。
另外,對于邊長比例不協調、形狀不規則的單元,以及場點靠近單元邊角的情況,將遠離場點的區域做細分是不必要的。為了很快地收斂,只需將投影點所在區域劃分出來,得到一個比例較為規則的小塊(陰影部分),然后按照圖1中分級細分方案進行細分,小塊以外區域保持不變,如圖5所示。
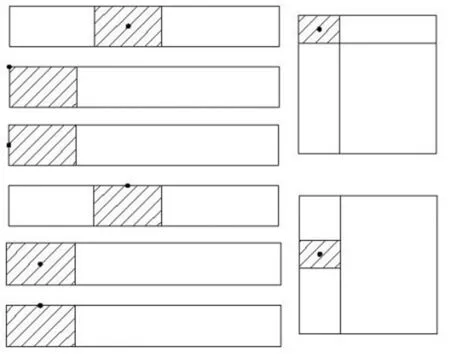
圖5 特殊情況下的細分方法Fig.5 Some especial cases for subdivision
5 數值算例
5.1 預估擬奇異性
對于任意不規則單元,可用表2中臨界接近度預估此種情況下是否存在擬奇異性。單元頂點和近場點的投影點坐標如圖6所示,投影點落在不規則單元的一頭。
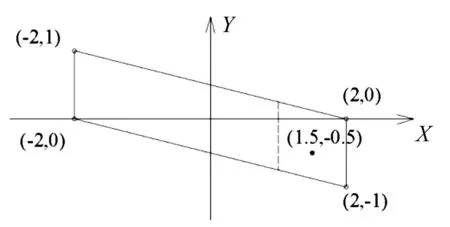
圖6 任意不規則單元和近場點的投影點Fig.6 The arbitrary irregular element and the subpoint
首先根據表2中②號點的臨界接近度E0作判斷:
t/l≥0.130
(17)
得到臨界距離為0.333 0,其中l取為長短邊的平均值,那么當近場點到單元距離t不小于0.333 0時,一定不存在擬奇異性。當t小于0.333 0時,將投影點所在部分劃分出來(虛線將Y軸右半部分單元平分),再根據表2中①號點的臨界接近度E0作判斷:
t/l≤0.150 5
(18)
得到臨界距離為0.152 8,其中l取為投影點所在子單元的長短邊平均值,那么當近場點到單元距離t不超過0.152 8時,一定存在擬奇異性。采用十點高斯積分,k=1 rad/m,t分別為0.333 0、0.3、0.2和0.152 8時,對應的擬奇異積分(分別為IR-1、IR-2、IR-3、IR-4)和誤差(分別為Er-1、Er-2、Er-3、Er-4)隨細分次數的收斂性曲線如圖7所示。
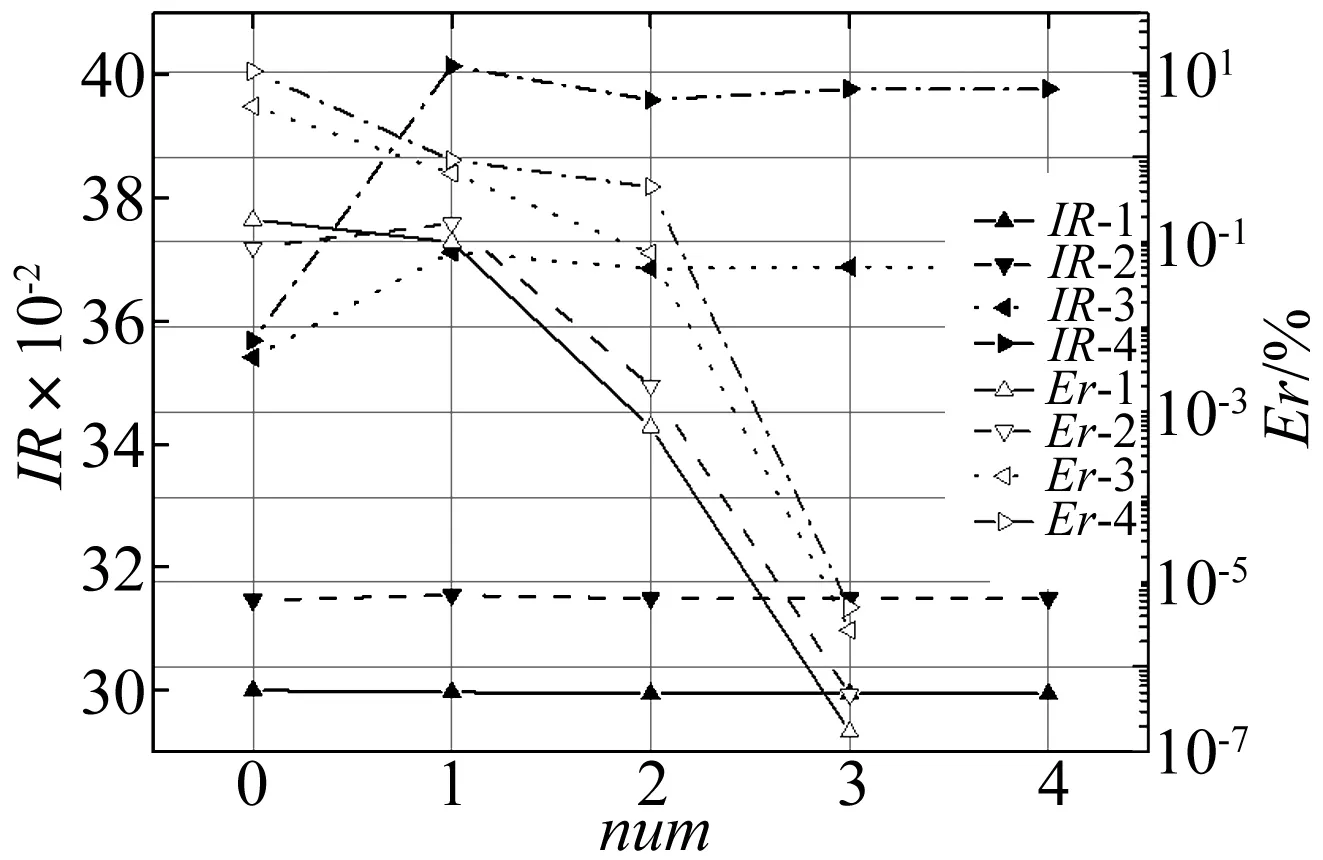
圖7 任意單元和近場點的擬奇異積分收斂性曲線Fig.7 The convergence curves of the nearly singular integrals on the arbitrary element
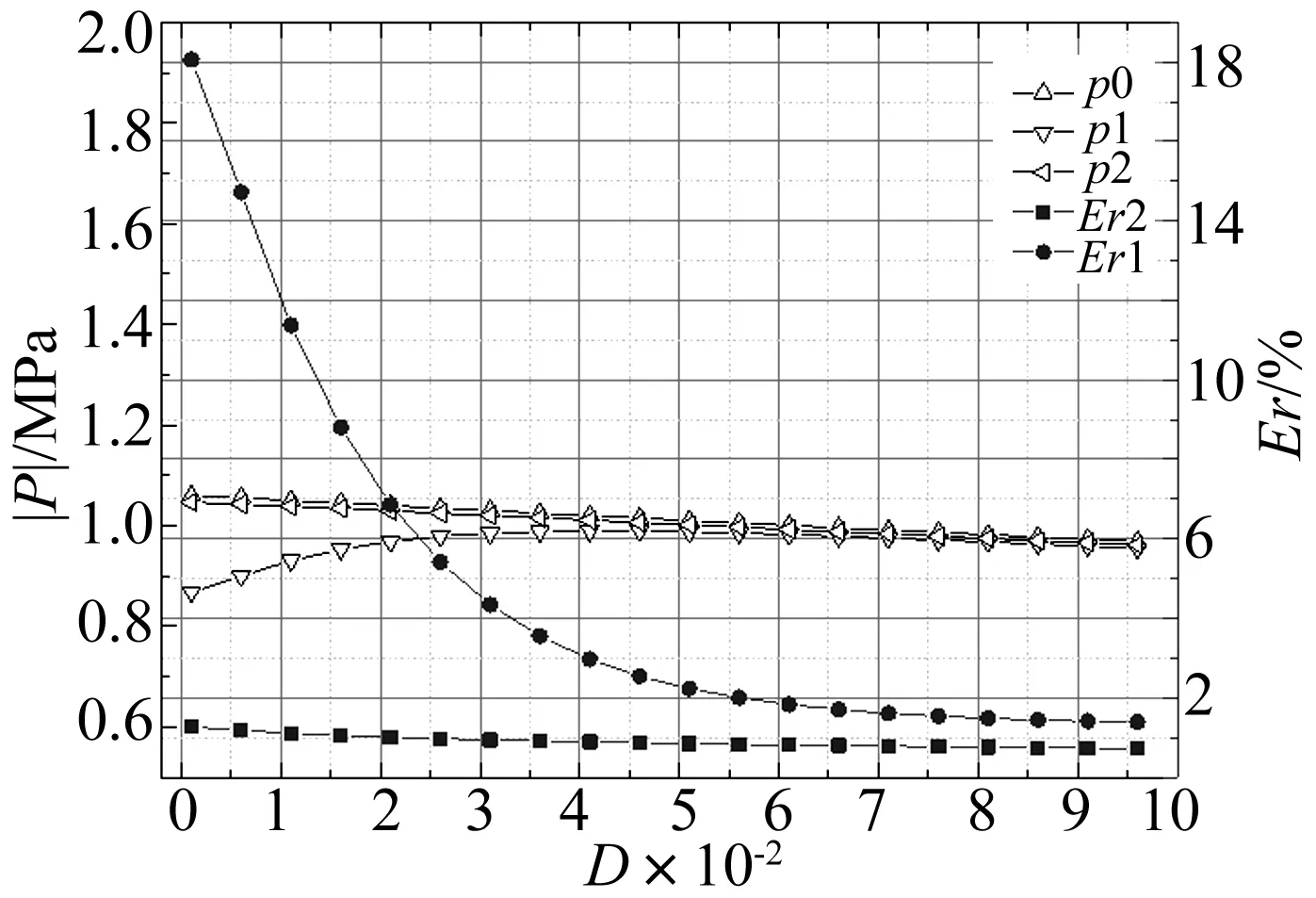
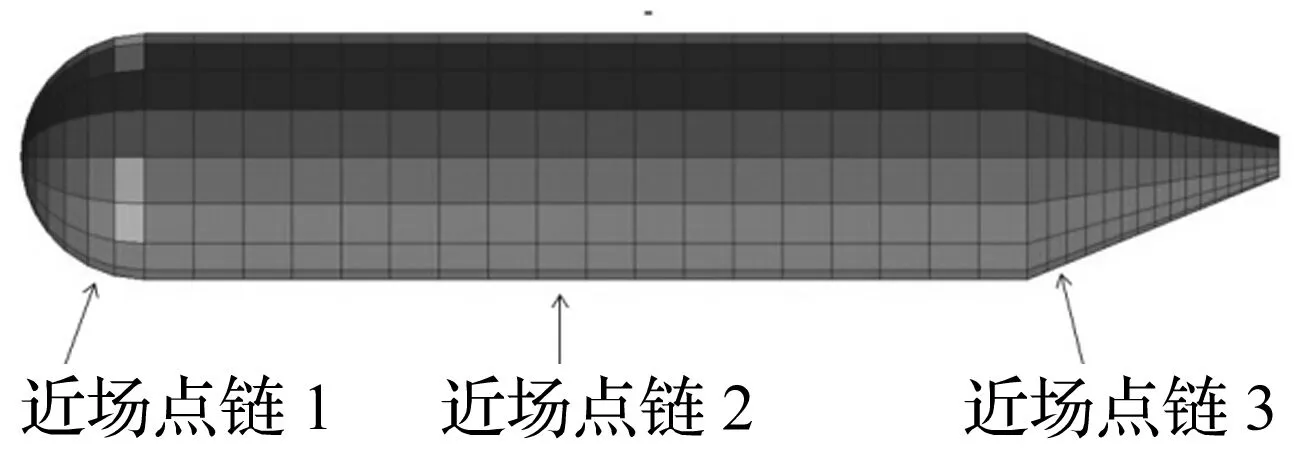
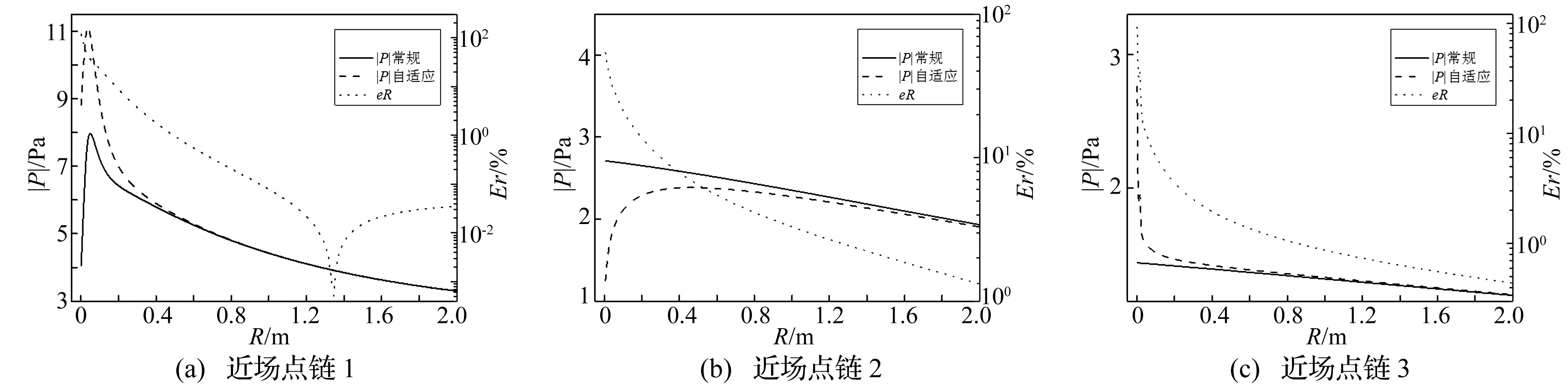
從圖7看出,不細分時IR-1和IR-2是收斂的,IR-3和IR-4是不收斂的,表明t為0.333 0和0.3時不存在擬奇異性,t為0.2和0.152 8時存在擬奇異性。這符合前文中t不小于0.333 0時一定不存在擬奇異性和t不超過0.152 8時一定存在擬奇異性的預計,也顯示了0.152 8 對于某些典型問題,利用臨界接近度能很快判斷是否存在擬奇異性。例如薄板聲輻射計算中,厚度為多少才算是“薄板”值得探究。實際聲學意義上的薄板并不是由板的長寬厚相對比例決定的,而是依據計算時單元尺寸與厚度之比。將圖8中的矩形平板劃分一致的矩形單元(不要求單元都為正方形),那么上下表面的單元是重合的,節點作為近場點,其相對位置固定。采用十點高斯積分,根據計算時使用單元的類型和臨界接近度得出聲學薄板的臨界厚度如表4所示,其收斂性已驗證,l為單元長短邊的平均值。厚度低于此臨界值的板為聲學薄板,需要處理擬奇異性。 圖8 矩形薄板網格Fig.8 The rectangular thin plate grid 單元類型臨界厚度/m常單元0.1505l線性單元0.04l二次單元0.1325l不連續線性單元0.11l不連續二次單元0.13l 5.2 脈動球聲輻射 以水中脈動球聲輻射為例驗證方法的正確性,將球體劃分242個四邊形單元,如圖9所示。半徑a=1 m,c=1 500 m/s,ρ=1 000 kg/m3,vn=1 m/s,k=1 rad/m。沿半徑方向距離球心R=1.001~1.1 m平均分布若干近場點,近場點與球體相對距離為D=(R-a)/a,與球心距離為R的場點聲壓解析解為 (19) 圖9 球體網格模型Fig.9 The spherical grid 圖10 兩種邊界元的計算對比曲線Fig.10. The results and errors with two methods 從圖10看出,聲壓幅值曲線p2與p0十分吻合,p1與p0有一定差距,而且D越小差距越大,這一點在誤差曲線Er1和Er2上可以更清晰地看到。在D的整個區間上,Er2都是小于Er1的,Er1變化較劇烈,而Er2相對平穩;Er1最大值超過18%,而Er2一直在1%左右。這些情況說明常規邊界元適用于計算遠場聲壓,計算近場聲壓則難以保證精度,本文的分級細分自適應邊界元法能有效計算近場聲壓。二者計算時間基本相同,因為對靠近場點的單元進行細分的計算量相對于總體計算量十分微小。對于聲學分析,采用平均細分法、式(15)或“對角線準則”所得到的場點聲壓與本文分級細分法計算結果并無差別,卻會產生更多子單元和額外計算量。 5.3 回轉殼聲輻射 如圖11所示,回轉殼由半球殼、圓柱殼和圓錐殼組成,半球體半徑為1 m,圓柱體長7 m,圓錐體高2 m,上端面半徑為0.16 m,表面統一振速為vn=1×10-5m/s,其它參數同上。分別沿半球、圓柱和圓錐表面單元中心法線設置3條近場點鏈,距離R為0.001~2 m。三個單元平均邊長l分別為0.29、0.39和0.26 m,故滿足式(16)的num皆為4。分別用常規高斯積分方法和自適應積分方法計算這些近場點聲壓,結果如圖12所示,其中eR是常規方法計算結果與自適應方法計算結果的誤差絕對值。 自適應方法中num取4和6的計算結果相等,說明num為4時結果已經收斂,圖12中僅展示num取4的曲線。可看出兩種積分方法的計算結果曲線的近場差別比脈動球算例更加顯著, 而且eR降到約1%所需的R也更大,這個現象說明常規積分方法的近場不精確程度也會受到結構尺寸的影響。 圖11 回轉殼網格模型Fig.11 The rotative shell grid 圖12 3條近場點鏈聲壓和誤差曲線Fig.12 The sound pressures and absolute errors of the 3 chains of near-field points 對于邊界元中的擬奇異積分問題,本文鑒于自適應精確積分的思想提出一種自適應分級細分方法,不需要迭代和判斷就能夠準確有效地計算任意近場點的擬奇異積分,所需子單元更少,且精度可以控制,其靈活性和高效性是一些已有方法所不具備的。接近度的研究為擬奇異積分的計算和預估擬奇異性程度提供理論基礎,具有一定的實用價值。 收斂性分析發現:單元上靠近場點的區域對擬奇異性的影響遠遠大于遠離場點的區域,梯度化地對待遠近區域能較好地考慮奇異性的機理,節省計算量。通過對接近度的研究發現:擬奇異性強弱由場點與單元的相對位置決定,并非單純由近場點到單元距離決定。 數值分析表明:在預估任意不規則單元和近場點是否存在擬奇異性時,臨界接近度可作為判斷擬奇異性存在與否的充分條件而非必要條件。對于薄板聲輻射問題,聲學意義上的薄與厚并不是由板的尺寸相對比例決定的,而要以接近度為參考,不同類型的計算單元所對應的臨界厚度也不相同。常規邊界元積分方法近場計算精度較低,其不精確程度也會受到結構尺寸的影響。 [1] 李善德, 黃其柏, 李天勻. 新的對角形式快速多極邊界元法求解聲學 Helmholtz 方程[J]. 物理學報, 2012,61(6): 64301. LI Shande, HUANG Qibai, LI Tianyun. A new diagonal form fast multipole boundary element method for solving acoustic Helmholtz equation[J]. Acta Physica Sinica, 2012, 61(6): 64301. [2] 白楊, 汪鴻振. 聲學-結構設計靈敏度分析[J]. 振動與沖擊,2003, 22(3):43-45. BAI Yang, WANG Hongzhen. Acoustic-structural design sensitivity analysis[J]. Journal of Vibration and Shock, 2003,22(3):43-45. [3] 楊迎春, 周其斗. 運動介質中奇異邊界元積分式的精確求解[J]. 振動與沖擊, 2011, 30(3): 242-245. YANG Yingchun, ZHOU Qidou. Accurate calculation of weak singular integrals in boundary element method in moving flows[J]. Journal of Vibration and Shock, 2011, 30(3): 242-245. [4] 張耀明, 孫翠蓮, 谷巖. 邊界積分方程中近奇異積分計算的一種變量替換法[J]. 力學學報, 2008, 40(2): 207-214. ZHANG Yaoming, SUN Cuilian, GU Yan. The evaluation of nearly singular integrals in the boundary integral equations with variable transformation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(2): 207-214. [5] 牛忠榮, 張晨利, 王秀喜. 邊界元法分析狹長體結構[J]. 計算力學學報, 2003, 20(4): 391-396. NIU Zhongrong, ZHANG Chenli, WANG Xiuxi. Boundary element analysis of the thin-wall structures[J]. Chinese Journal of Computational Mechanics, 2003, 20(4): 391-396. [6] TANAKA M, SLADEK V, SLADEK J. Regularization techniques applied to boundary element methods[J]. Applied Mechanics Reviews,1994, 47(10): 457-499. [7] ZHANG Y, GU Y, CHEN J. Stress analysis for multilayered coating systems using semi-analytical BEM with geometric non-linearities[J]. Computational Mechanics, 2011, 47(5): 493-504. [8] NIU Z, CHENG C, ZHOU H, et al. Analytic formulations for calculating nearly singular integrals in two-dimensional BEM[J]. Engineering Analysis with Boundary Elements, 2007, 31(12): 949-964. [9] ZHOU H, NIU Z, CHENG C, et al. Analytical integral algorithm in the BEM for orthotropic potential problems of thin bodies[J]. Engineering Analysis with Boundary Elements, 2007, 31(9):739-748. [10] ZHOU H, NIU Z, CHENG C, et al. Analytical integral algorithm applied to boundary layer effect and thin body effect in BEM for an isotropicpotential problems[J]. Computers & Structures, 2008, 86(1516):1656-1671. [11] NIU Z, ZHOU H. The natural boundary integral equation in potential problems and regularization of the hypersingular integral[J]. Computers & Structures, 2004, 82(2):315-323. [12] DAVIES T G, GAO X. Three-dimensional elasto-plastic analysis via the boundary element method[J]. Computers and Geotechnics,2006, 33(3):145-154. [13] KITA E, KAMIGA N. Error estimation and adaptive mesh refinement in boundary element method, an overview[J]. Engineering Analysis with Boundary Elements, 2001,25(7):479-495. [14] WEI Y, WANG Y, CHANG S, et al. Numerical prediction of propeller excited acoustic response of submarine structure based on CFD, FEM and BEM[J]. Journal of Hydrodynamics, 2012, 24(2): 207-216. [15] CROAKER P, KESSISSOGLOU N, MARBURG S. Strongly singular and hypersingular integrals for aeroacoustic incident fields[J]. International Journal for Numerical Methods in Fluids, 2015, 77(5): 274-318. [16] DONG Y, ZHANG J, XIE G, et al. A general algorithm for the numerical evaluation of domain integrals in 3D boundary element method for transient heat conduction[J]. Engineering Analysis with Boundary Elements, 2015, 51: 30-36. [17] DAVIES T G, GAO X. Three-dimensional elasto-plastic analysis via the boundary element method[J]. Computers and Geotechnics, 2006, 33(3):145-154. [18] GAO X W, YANG K, WANG J. An adaptive element subdivision technique for evaluation of various 2D singular boundary integrals[J]. Engineering Analysis with Boundary Elements, 2008, 32(8): 692-696. [19] LI Y, YE J H. The interaction between membrane structure and wind based on the discontinuous boundary element[J]. Science China Technological Sciences, 2010, 53(2): 486-501. [20] 王靜, 高效偉. 基于單元子分法的結構多尺度邊界單元[J].計算力學學報, 2010, 27(2): 258-263. WANG Jing, GAO Xiaowei. Structural multi-scale boundary element method based on element subdivision technique[J]. Chinese Journal of Computational Mechanics, 2010, 27(2): 258-263. [21] QU S, CHEN H, LI S. Adaptive integration method based on sub-division technique for nearly singular integrals in near-field acoustics boundary element analysis[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2014,33(1): 27-46. [22] GAO X W,DAVIES T G. Adaptive integration in elasto-plastic boundary element analysis[J]. Journal of the Chinese Institute of Engineers, 2000, 23(3):349-356. [23] ZHANG J, TANAKA M, MATSUMOTO T. Meshless analysis of potential problems in three dimensions with the hybrid boundary node method[J]. International Journal for Numerical Methods in Engineering, 2004, 59(9): 1147-1166. [24] ZHANG J, QIN X, HAN X, et al. A boundary face method for potential problems in three dimensions[J]. International Journal for Numerical Methods in Engineering, 2009, 80(3): 320-337. [25] KANG S C, IH J G. On the accuracy of nearfield pressure predicted by the acoustic boundary element method[J]. Journal of Sound and Vibration, 2000, 233(2): 353-358. Adaptive method for calculating nearly singular integrals in acoustic boundary elements MIAO Yuyue1,2, LI Tianyun1,2,3, ZHU Xiang1,2, ZHANG Guanjun1,2, GUO Wenjie1,2 (1. School of Naval Architecture and Ocean Engineering,Huazhong University of Science & Technology, Wuhan 430074,China;2.Hubei Key Laboratory of Naval Architecture & Ocean Engineering Hydrodynamics, Wuhan 430074,China;3.National Key Laboratory on Ship Vibration & Noise, Wuhan 430064,China) An adaptive method was presented to calculate nearly singular integrals in acoustic boundary elements. The element was subdivided into subelements hierarchically so as to remove the near singularity by transforming the integral over the initial element to Gauss integrals over subelements. Based on this method, the near singularity was thoroughly studied and the concept of proximity was described. The critical proximity can be used as the criterion for calculating nearly singular integrals and to predict the existence of near singularity. Compared with previous methods, the adaptive method is more flexible and efficient. The integral precision can be adjusted and is not restricted by the positions of near-field points. It is found that the positional relationships between near-field points and the element have important effect on nearly singular integrals. The work provides more understanding and choice to the problem of near singularity in acoustic boundary elements. boundary element; nearly singular intergral; adaptivity; proximity 國家自然科學基金(51379083;51479079);高等學校博士學科點專項科研基金(20120142110051) 2015-09-09 修改稿收到日期:2015-12-05 繆宇躍 男,博士生,1988年生 李天勻 男,教授,博士生導師,1969年生 E-mail:ltyz801@mail.hust.edu.cn TB532 A 10.13465/j.cnki.jvs.2017.02.004

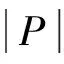
6 結 論

