基于雙重猶豫模糊語言的多屬性決策方法

王中興，陳紹松，何婷婷，賈 欣

(廣西大學 數學與信息科學學院， 南寧 530004)

基于雙重猶豫模糊語言的多屬性決策方法

王中興，陳紹松，何婷婷，賈 欣

(廣西大學 數學與信息科學學院， 南寧 530004)

結合語言術語集和雙重猶豫模糊集給出了雙重猶豫模糊語言集的定義，并給出雙重猶豫模糊語言數的運算法則和比較方法。針對屬性值為雙重猶豫模糊語言數的多屬性決策問題，提出集結雙重猶豫模糊語言信息的雙重猶豫模糊語言加權平均算子以及基于此算子的多屬性決策方法，并將所提的決策方法應用于選址建廠問題以說明其可行性和有效性。

決策方法；雙重猶豫模糊語言；集成算子；比較方法

自Torra[1]提出猶豫模糊集理論以來，該理論引起了學者的廣泛關注并得到了迅速發展。Xu和Xia[2]基于猶豫模糊集建立了集結猶豫模糊決策信息的猶豫模糊加權平均(HFWA)算子、猶豫模糊有序加權平均(HFOWA)算子、猶豫模糊混合加權平均(HFHA)算子等，并將其應用于多屬性決策問題中。西班牙學者Rodriguze等[3]在定性的環境中提出了猶豫模糊語言術語集(HFLTS)，給出max-lower算子和min-upper算子，進而提出了一種解決基于猶豫模糊語言術語集的多屬性決策問題的方法。針對猶豫模糊集對非隸屬度缺乏考慮這一情況，Zhu和Xu等[4]提出了雙重猶豫模糊集，它的隸屬度和非隸屬度均為[0,1]之間多個可能的數值，表現出更強的模糊信息處理能力。

在多屬性決策過程中，由于決策環境的復雜性，在對諸如汽車性能等評價中，多數采用“優秀”、“良好”和“一般”等模糊語言信息來表述[5]。然而，語言評價暗含準則隸屬于語言值的程度為1，不能刻畫非隸屬度和猶豫度。為了解決這類問題，Yang等[6]提出了雙語言數的概念，并給出了一種級別高關系的多屬性決策方法。Wang等[7]在直覺模糊集的基礎上定義了直覺語言集、直覺語言數及其比較方法，給出直覺語言加權算術平均(IL-WAA)算子和直覺語言加權幾何平均(IL-WGA)算子，并把它們應用于多屬性決策中。Liu等[8]拓展了直覺語言集定義了直覺不確定語言集，提出了集結直覺不確定語言信息的直覺不確定語言的加權算術平均(IULWAA)算子。Lin等[9]在猶豫模糊集的基礎上進一步拓展了直覺模糊語言集和直覺不確定語言集，提出了猶豫模糊語言集和不確定猶豫模糊語言集，并給出了相應的多屬性決策方法。

由于雙重猶豫模糊集相對于猶豫模糊集在處理模糊信息時具有更強的表現力。本文將在語言術語集和雙重猶豫模糊集的基礎上，進一步拓展猶豫模糊語言集，定義雙重猶豫模糊語言集，并提出一種集結雙重猶豫模糊語言信息的多屬性決策方法。

1 預備知識

為了便于研究，下面給出語言術語集、猶豫模糊集和雙重猶豫模糊集等的有關概念。

1.1 語言術語集

定義1[10]設S={sα|α=0,1,…,τ}是一個下標均為非負整數組成的語言術語集,其中τ為偶數，且S滿足下列條件：

① 若α>β，則sα>sβ；

② 存在負算子neg(sα)=sβ,使得α+β=τ；

③ 若sα≥sβ，則max(sα,sβ)=sα；

④ 若sα≤sβ，則min(sα,sβ)=sα。

基于連續語言術語集，給出相應的語言術語運算法則：

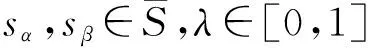
①sα⊕sβ=sα+β；

②λsα=sλα。

1.2 猶豫模糊語言集

定義 3[9]設X為一個給定的集合，則X上的猶豫模糊語言集E定義為：

其中h(x)由[0,1]中的不同數組成的集合，表示sθ(x)的隸屬度。為了方便，記a=〈sθ(a),h〉為一個猶豫模糊語言元(HFLE)。

1.3 雙重猶豫模糊集

Zhu和Xu等[4]在猶豫模糊集的基礎上增加考慮了非隸屬度，提出了雙重猶豫模糊集。

定義4[4]設X為一個給定的集合，稱D={〈x,h(x),g(x)〉]|x∈X}為雙重猶豫模糊集(DHFS)。其中h(x),g(x)分別由[0,1]區間上的若干個不同數構成，分別表示x屬于集合D的所有可能的隸屬度和非隸屬度，且滿足：

其中：γ+=max{γ|γ∈h(x)}；η+=max{η|η∈g(x)}。

2 雙重猶豫模糊語言集以及雙重猶豫模糊數的比較

2.1 雙重猶豫模糊語言集

猶豫模糊語言集只考慮了隸屬度，而對非隸屬度缺乏考慮。在實際的決策過程中，如在對某汽車的舒適性進行評價時，人們認為該汽車“舒適”可能為“0.6和0.7”，而認為“不舒適”可能為“0.1和0.2”，此時猶豫模糊語言集并不能給予恰當的表達。在諸多的決策過程中表明：非隸屬度也是十分重要的決策信息。因此，本文將在猶豫模糊語言集的基礎上增加考慮語言值的非隸屬度，提出雙重猶豫模糊語言集。

定義5 設X為一個給定的集合，則雙重猶豫模糊語言集可以描述為如下的形式：

其中： sθ(x)∈S(S為語言術語集)； h(x)，g(x)分別由[0,1]區間上的若干個不同數構成，分別表示x隸屬于和非隸屬于sθ(x)的程度,且滿足

其中γ+=max{γ|γ∈h(x)}，η+=max{η| η∈g(x)}。

為了方便，稱三元組d=〈sθ(d),h,g〉為一個雙重猶豫模糊語言數。當h,g中分別只含有1個元素時：如h只含有1個元素且g=φ(φ表示空集)，雙重猶豫模糊語言數退化為雙語言數[6]，雙重猶豫模糊語言數退化為直覺語言數[7]；如h≠φ且g=φ，雙重猶豫模糊語言數退化為猶豫模糊語言數[9]。

基于語言變量和直覺模糊數的運算，給出雙重猶豫模糊語言數的運算法則如下：

定義6 設d1=〈sθ(d1),h1,g1〉， d2=〈sθ(d2),h2,g2〉為任意的2個雙重猶豫模糊語言數，則：

① d1⊕d2=〈sθ(d1)+θ(d2),∪γ1∈h1,γ2∈h2{γ1+γ2-γ1γ2},∪η1∈g1,η2∈g2{η1η2}〉；

② d1?d2=〈sθ(d1)×θ(d2),∪γ1∈h1,γ2∈h2{γ1γ2},∪η1∈g1,η2∈g2{η1+η2-η1η2}〉 ；

③ λd1=〈sλθ(d1),∪γ1∈h1{1-(1-γ1)λ},∪η1∈g1{(η1)λ}〉；

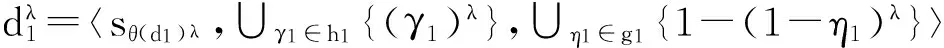
容易驗證,雙重猶豫模糊語言數的運算具有如下性質。

定理1 設d1=〈sθ(d1),h1,g1〉，d2=〈sθ(d2),h2,g2〉為任意的兩個雙重猶豫模糊語言數，λ,λ1,λ2>0，則

① d1⊕d2=d2⊕d1；

② d1?d2=d2?d1；

③ λd1⊕λd2=λ(d2⊕d1)；

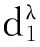
⑤ λ1d1+λ2d1=(λ1+λ2)d1；

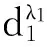
證明 由定義6中雙重猶豫模糊語言數的運算法則①和②可知，①和②顯然成立。

由運算法則①和③有：

又因為

則

所以λd1⊕λd2=λ(d1⊕d2)成立。

由運算法則②和④，類似③的證明方法，可得④成立。

由運算法則①和③有：

又因為

所以λ1d1+λ2d1=(λ1+λ2)d1成立。

由運算法則②和④，類似⑤的證明方法，可得⑥成立。

2.2 雙重猶豫模糊語言數的比較

定義7 設d=〈sθ(d),h,g〉為任意的一個雙重猶豫模糊語言數，則d的得分函數S(d)和精確函數H(d)分別定義為：

(1)

(2)

其中： θ(d)表示sθ(d)∈S的下標； τ為語言術語集S的粒度；#h,#g分別為h,g中元素的個數。

基于得分函數S(d)和精確函數H(d)，給出雙重猶豫模糊語言數的比較方法：

定義8 設d1=〈sθ(d1),h1,g1〉，d2=〈sθ(d2),h2,g2〉為任意兩個雙重猶豫模糊語言數，那么有：

① 若S(d1)>S(d2)，則d1>d2；

② 若S(d1)=S(d2)，那么：若H(d1)>H(d2)，則d1>d2，若H(d1)=H(d2)，則d1=d2。

3 雙重猶豫模糊語言集成算子

根據雙重猶豫模糊語言數的運算法則，給出雙重猶豫模糊語言集成算子如下：

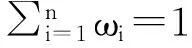
證明 用數學歸納法如下：

1) 當n=2時，由定義8中的運算法則①和③有：

2) 假設當n=k時定理2成立，即

則當n=k+1時，有：

因此，當n=k+1時，定理2也成立，由1)和2)可知，對任何n定理2都成立。

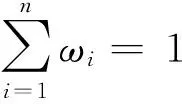
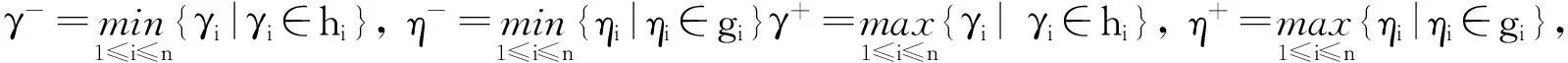
那么

則

其中#h,#g分別為DHFLWA算子集成結果值中隸屬度和非隸屬度的個數。

綜上可得：

所以

同理可證

所以

4 基于DHFLWA算子的多屬性決策方法

步驟1 利用DHFLWA算子對決策矩陣R=(rij)m×n的第i行進行集成得到方案Xi綜合評價值Ri(i=1,2,…,m)；

步驟2 利用式(1)和(2)計算方案Xi的綜合評價值Ri的得分函數S(Ri)和精確函數H(Ri)(i=1,2,…,m)；

步驟3 利用S(Ri)和H(Ri)的大小按定義8對Xi(i=1,2,…,m)進行排序并擇優。

5 算例分析

某電子集團公司將要選擇一個新地方建造新廠，共有3種合適的地點X1,X2,X3可供選擇。該公司的決策者主要依據成本(C1)、交通(C2)、環境(C3)等3種屬性進行選址建廠。公司給出屬性權重向量為ω=(0.3,0.5,0.2),決策者均采用七粒度語言術語集S={s0,s1=,…,s6}對方案Xi(i=1,2,3)進行評價，是到的雙重猶豫模糊語言評價矩陣見表1。

表1 評價矩陣Table 1 The evaluation matrix

以下利用本文提出的決策方法對備選地點X1,X2,X3進行排序和擇優。

步驟1 利用DHFLWA算子對方案Xi的雙重猶豫模糊語言評價值進行集成得到方案Xi綜合屬性值Ri，i=1,2,3：

R1=〈s2.9,{0.589 8, 0.612 7, 0.633 1, 0.653 6, 0.636 7, 0.657 1, 0.693 3}, {0.174 1, 0.213 2}〉

R2=〈s3.6,{0.637 8, 0.653 6, 0.667 7, 0.682 2}, {0.244 9, 0.200 0, 0.276 6, 0.225 9}〉

R3=〈s2.2,{0.734 4, 0.783 1}, {0.100 0, 0.114 9, 0.123 1, 0.141 4}〉

步驟2 利用式(1)分別計算每個方案的綜合評價值Ri(i=1,2,3)的得分函數S(Ri)：

S(R1)=0.299 5,S(R2)=0.366 0,S(R1)=0.257 5

步驟3 因為S(R2)>S(R1)>S(R3)，故R2>R1>R3,所以方案X2?X1?X3,即地點X2為選址建廠的最佳選擇。

6 比較分析

選擇Wang等[6]基于直覺語言的多屬性決策方法和Lin等[8]基于猶豫模糊語言的多屬性決策方法與本文提出的決策方法進行比較分析。應用本文提出的決策方法計算Wang等[6]中的算例(例1)和Lin等[8]中的算例(例2)，比較排序結果。

例1 一個多屬性決策問題，共有5個方案X1,X2,…,X5，5個屬性C1,C2,…,C5,其屬性權重為ω=(0.20,0.15,0.25,0.10,0.30)，決策者采用語言術語集S={s0,s1,…,s6}對方案進行評價，給出的決策信息如表2。

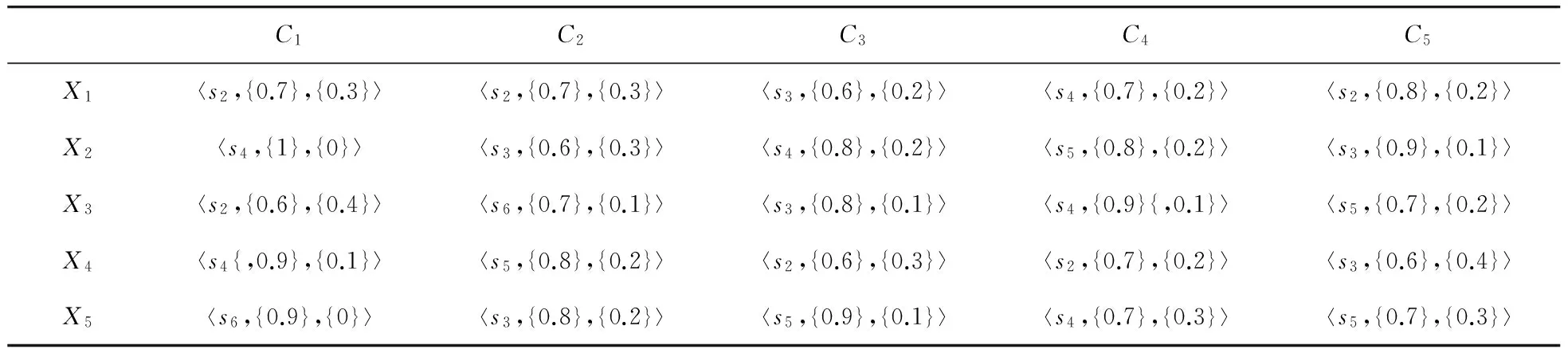
表2 屬性評價值Table 2 Attribute evaluation value

步驟1 利用DHFLWA算子對方案Xi的屬性值進行集成得到方案Xi綜合屬性值Ri(i=1,2,…,5)，R1=〈s2.6,{0.714 6}, {0.212 6}〉，R2=〈s3.65,{1},{0}〉，R3=〈s3.95,{0.742 7},{0.162 5}〉，R3=〈s3.95,{0.742 7},{0.162 5}〉，R5=〈s4.8,{0.827 8},{0}〉。

步驟2 利用式(1)分別計算每個方案的綜合屬性值Ri(i=1,2,…,5)的得分函數S(Ri)有：S(R1)=0.108 8，S(R2)=0.304 2,S(R3)=0.191 0,S(R4)=0.130 5,S(R5)=0.331 1。

步驟3 因S(R5)>S(R2)>S(R3)>S(R4)>S(R1)，故R5>R2>R3>R4>R1,所以S(Ri)有：S(R1)=0.108 8，S(R2)=0.304 2,S(R3)=0.191 0,S(R4)=0.130 5,S(R5)=0.331 1；

步驟4 因為S(R5)>S(R2)>S(R3)>S(R4)>S(R1)，故R5>R2>R3>R4>R1,所以方案X5>X2>X3>X4>X1,即方案X5為最佳方案。

以上方案的排序與Wang等[6]的排序結果完全相同，由此可見本文提出的決策方法可以處理評價值為直覺語言數的多屬性決策問題。

例2 假設有5個ERP系統X1,X2,…,X5可供選擇，在選擇最佳ERP系統時需要考慮4個評價屬性：功能和技術(C1)；匹配性(C2)；供應商能力(C3)；供應商信譽(C4)，其中屬性權重為ω=(0.3,0.2,0.4,0.1)。某公司聘請專家采用語言術語集S={s0,s1,…,s9}對5個ERP系統X1,X2,…,X5的屬性評價值如表3所示。

表3 ERP系統的屬性值Table3 Attribute value of ERP system

步驟1 利用DHFLWA算子對方案Xi的ERP系統屬性值進行集成得到方案Xi綜合ERP系統屬性值Ri，i=1,2,…,5：

R1=〈s3.3,{0.606 5, 0.628 5, 0.632 9, 0.644 3, 0.653 4, 0.657 5, 0.664 2, 0.665 5, 0.668 1, 0.680 4, 0.684 2, 0.686 7, 0.687 9, 0.690 4, 0.697 6, 0.705 3, 0.708 8, 0.711 1, 0.714 5, 0.717 8,0.728 3, 0.733 6, 0.736 7,0.754 4}〉

R2=〈s3.3,{0.507 3, 0.516 2, 0.560 9, 0.568 8, 0.626 6, 0.633 4, 0.667 2, 0.673 2, 0.529 6, 0.554 6, 0.538 1, 0.562 7, 0.580 7, 0.603 0, 0.610 2, 0.588 3, 0.643 5, 0.662 5, 0.649 9, 0.668 6, 0.682 2, 0.699 1, 0.688 0,0.704 6}〉

R3=〈s4.5,{0.466 5, 0.481 7, 0.533 7, 0.546 9, 0.619 9, 0.630 7, 0.508 1, 0.522 0, 0.570 0, 0.582 2, 0.649 5, 0.659 4, 0.527 6, 0.541 0, 0.587 1, 0.598 8, 0.663 4, 0.673 0, 0.564 4, 0.576 8, 0.619 3, 0.630 1, 0.689 6, 0.689 7}〉

R4=〈{s4.9,0.525 5, 0.541 2, 0.613 2, 0.626 0, 0.535 9, 0.555 1, 0.624 9, 0.937 3, 0.658 7, 0.670 0, 0.721 8, 0.731 0, 0.669 1, 0.680 0, 0.730 2, 0.739 2}〉

R5=〈s3.4,{0.476 8, 0.497 6, 0.531 3, 0.521 5, 0.540 5,0.571 3, 0.506 1, 0.525 7, 0.575 0, 0.548 3, 0.566 2, 0.588 1, 0.525 5, 0.543 3, 0.574 9, 0.566 0, 0.583 2, 0.595 3, 0.497 4, 0.517 3, 0.549 7, 0.540 3, 0.558 6,0.611 2}〉

步驟2 利用式(1)分別計算每個方案的綜合ERP系統屬性值Ri(i=1,2,…,5)的得分函數S(Ri)有：S(R1)=0.309 4, S(R2)=0.293 4, S(R3)=0.397 2, S(R4)=0.505 1, S(R5)=0.292 7。

步驟3 因為S(R4)>S(R3)>S(R1)>S(R2)>S(R5)故R4>R3>R1>R2>R5,所以方案X4>X3>X1>X2>X5,即方案X4為最佳方案。

以上方案的排序與Yang等[6]的排序結果完全相同，由此可見本文提出的決策方法可以處理評價值為猶豫模糊語言數的多屬性決策問題。

事實上，從適用范圍上看，設di=〈sθ(di),hi,gi〉(i=1,2,…,n)為n個雙重猶豫模糊語言數，當hi,gi中分別只含有1個元素時，雙重猶豫模糊語言數退化為直覺語言數。當hi≠φ且gi=φ時(φ表示空集)，雙重猶豫模糊語言數退化為猶豫模糊語言語言數。由例1和例2可以看出：本文提出的決策方法不僅能夠處理評價信息為雙重猶豫模糊語言信息型，還可以處理評價信息為直覺語言信息型和猶豫模糊語言信息型，表現出更強的模糊信息的處理能力，具有更廣泛的適用范圍。

7 結束語

雙重猶豫模糊語言集是對猶豫模糊語言集的進一步拓展。因此，本文首先在雙重猶豫模糊集和語言術語集的基礎上定義了雙重猶豫模糊語言集、雙重猶豫模糊語言數及其運算法則，給出了雙重猶豫模糊數的得分函數和精確函數，進而給出了雙重猶豫模糊數的一種排序方法。然后，針對雙重猶豫模糊語言的集成問題，提出了雙重猶豫模糊語言加權算術平均(DHFLWA)算子。最后，提出一種基于DHFLWA算子的多屬性決策方法。該方法解決了屬性值為雙重猶豫模糊語言數的多屬性決策問題，從而豐富和發展了模糊決策方法。

[1] TORRA V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.

[2] XU Z S,XIA M M.Hesitant fuzzy information aggregation in decision making[J].International Journal of Approximate Reasoning,2011，52(3):395-407.

[3] RODRIGUEZ R M,MARTINEZ L,HERRERA F.Hesitant fuzzy linguistic terms sets for decision making[J].IEEE Transactions on Fuzzy Systems,2012，20(1)：109-119.

[4] ZHU B,XU Z S,XIA M M.Dual hesitant fuzzy sets[J].Journal of Applied Mathematics,2012:879629.

[5] HERRERA F,HERRERA-Viedma E.Linguistic decision analysis:steps for solving decision problems under linguistic information[J].Fuzzy Sets and Systems,2000,115(1):67-82.

[6] YANG W E,WANG J Q,WANG X F.An outranking method for multi-criteria decision making with duplex linguistic information[J].Fzzy Sets and Systems,2012,198:20-33.

[7] 王堅強,李寒波.基于直覺語言集結算子的多準則決策方法[J].控制與決策,2010,25(10):1571-1574.

WANG Jianqiang,LI Hanbo.Multi-criteria decision-making method based on aggregation operators for intuitionistic linguistic fuzzy numbers[J].Control and Decision,2010，25(10):1571-1574.

[8] LIU P D,JIN F.Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making[J].Information Sciences,2012,205(1):58-71.

[9] LIN R,ZHAO X F,WEI G W.Models for selecting an ERP system with hesitant fuzzy linguistic information[J].Joural of Intelligent & Fuzzy System,2014，26(5):2155-2165.

[10]HERRERA F,HERRERA-Viedma E,VERDEGAY J L.A model of consensus in group decision making under linguistic assessments[J].Fuzzy Sets and Systems,1996;78(1):73-87.

[11]XU Z S.Deviation measures of linguistic preference relations in group decision making[J].The International Journal of Management Sciences,2005，33(3):249-254.

[12]戴躍強，徐澤水，李琰,等.語言信息評估新標度及其應用[J].中國管理科學,2008,16(2):145-149.

DAI Yueqiang,XU Zheshui,LI Yan,et al.New evaluation scale of linguistic information and its application[J].Chinese Journal of Management Science,2008，16(2):145-149.

(責任編輯 陳 艷)

An Approach to Multiple Attribute Decision Making Based on Dual Hesitant Fuzzy Linguistics

WANG Zhong-xing, CHEN Shao-song, HE Ting-ting, JIA Xin

(Institute of Mathematics and Information Science, Guangxi University, Nanning 530004, China)

The dual hesitant fuzzy linguistic set is defined which is combined with linguistic term set and dual hesitant fuzzy set, at the meantime, some operational laws and comparison method of the dual hesitant fuzzy linguistic numbers are also given. Considering the attribute value is hesitant fuzzy linguistic number during the multiple attribute decision making, the dual hesitant fuzzy linguistic weighted average operator is proposed and based on the operator a multiple attribute decision making method is given. Finally, the method is applied to the factory location selection problem to verify its feasibility and effectiveness.

decision making method; dual hesitant fuzzy linguistic sets; aggregation operators; comparative method

2016-09-09

國家自然科學基金資助項目(71571054)

王中興(1962—)，男，教授,主要從事優化與決策研究，E-mail:zxwgx@126.com； 通訊作者 陳紹松(1990—)，男(土家族)，碩士研究生，主要從事優化與決策研究，E-mail:chenshaosong@126.com。

王中興，陳紹松，何婷婷，等.基于雙重猶豫模糊語言的多屬性決策方法[J].重慶理工大學學報(自然科學)，2017(1):124-133.

format：WANG Zhong-xing, CHEN Shao-song, HE Ting-ting, et al.An Approach to Multiple Attribute Decision Making Based on Dual Hesitant Fuzzy Linguistics[J].Journal of Chongqing University of Technology(Natural Science)，2017(1):124-133.

10.3969/j.issn.1674-8425(z).2017.01.020

O21；C934

A

1674-8425(2017)01-0124-10