神經網絡在機械臂軌跡規劃中的應用研究

唐瑞華

?

神經網絡在機械臂軌跡規劃中的應用研究

唐瑞華

巢湖學院，安徽 巢湖 238000

介紹了機械臂運動學的理論基礎以及在 MATLAB 中的正運動學仿真，驗證了模型的合理性和有效性。然后重點探討了神經網絡實現基本軌跡的求逆和跟蹤，對關節角允許范圍內的隨機角度進行了訓練測試，結果良好。

神經網絡；機械臂；軌跡規劃

引言

隨著機械電子科學技術的高速發展，工業機器人之一的機械臂一直在努力提高工作效率和節約生產成本，從而提高產品的性能。智能型機械臂集成了計算機技術、軟件技術、電子技術等，在實際工作過程中能夠對工作環境做出敏捷的反應，從而保證工作質量。

在機械臂的現實應用過程中，評價它工作好壞的主要標準是工作的高效性和可靠性。實際工作過程中會出現啟動時的不穩定、定位時的精度等難題，大多數會造成硬件結構和機械構件發生一定的磨損。因此，為了改變不穩定性，就需要我們規劃更好的運動軌跡，從而讓它表現出光滑而又連續的平滑曲線。理論上它的抖動和角度突變這種問題是避免不了的，但我們能盡量減小磨損。平穩運行必須是建立在規劃好它的末端運動軌跡的基礎，然后通過大量仿真結果來分析它的具體運動規律[1]。

1 軌跡規劃概述

根據機械臂要執行任務的不同來劃分機械臂軌跡的規劃，大致可以分為兩種：一種是給始末點，只要讓機械臂末端從始點運動到終點，至于中間是怎么走的，它不做要求；另一種是給定末端的軌跡在讓它沿著軌跡運動[2]。

機械臂軌跡規劃往往是在理解了機械臂所需要滿足的角加速度、角速度、角加速度變化量和生成該軌跡的方式建立在沿力矩等一系列約束的基礎上，而且過程也需要一些約束條件，還要考慮是在哪種空間進行規劃比較方便。

（1）任務描述；

（2）將計算得到的軌跡轉化計算機語言，進而在計算機內來描述通過計算所獲得的軌跡；

（3）實時計算。通常處理這類問題時把它設計成一個軌跡規劃器。這個規劃器相當于一個盒子，不需要知道里面的結構和布局，只要給它一定的約束條件，就可以得出我們想要的結果了。所以我們只需輸入相關軌跡約束并對軌跡進行簡單計算機描述，然后它就能夠簡化任務描述，至于規劃過程中的細節問題不需要弄清楚，系統本身會處理掉這類問題[3]。

在給定機械臂運行軌跡的始末端之間，肯定有很多種可能的曲線，這些曲線都可能是要求解的軌跡。如果在計算過程中某些參數必須用關節坐標表示，就可以應用逆運動學來將笛卡爾坐標值轉換為關節坐標值。關節變量和機械臂運行之間是關于時間的函數，同時規劃該函數的一、二階導數分別來描述機械臂運動過程中機械臂各關節的角速度變化和角加速度變化規律。

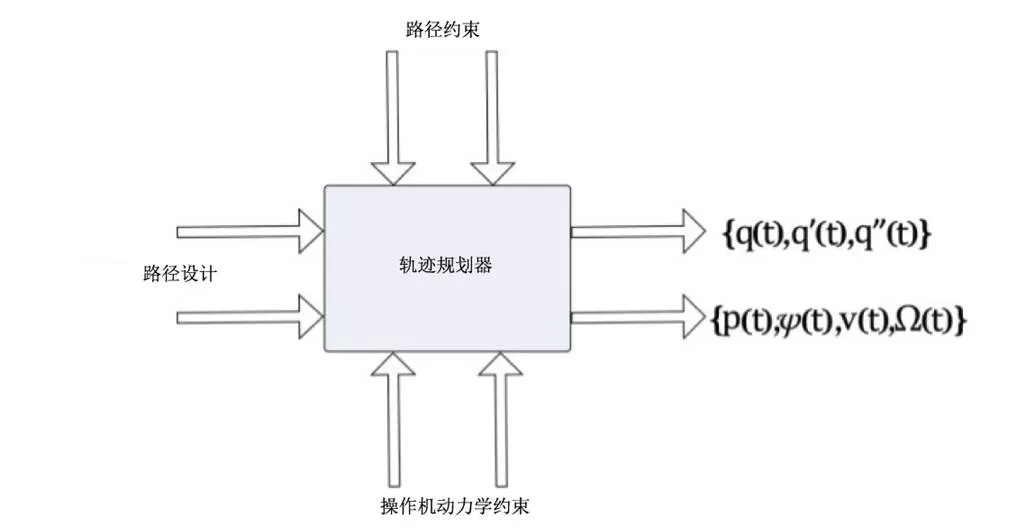
圖1 軌跡規劃原理圖

機械臂的軌跡選擇取決于要規劃的曲線，但是不管選定在哪種空間下，我們的目的都是一樣的。對于不同任務的機械臂而言，不管選用哪種函數規劃軌跡，這些曲線都要保持連續性，然而對于不同的軌跡要求對應不同的規劃方法。不管怎樣，實現規劃都離不開插值計算，依照軌跡要求精度的高低將插值計算劃分為如下兩種：（1）定時插補；（2）定距插補。

2 神經網絡模型

ANN是通過模擬人腦神經系統而建立起來的一種模型，并且具有并行處理信息的能力，為復雜系統求解提供了一種新的解決方法。ANN的核心是針對不同結構類型算法，其中以誤差反向傳播算法——BP神經網絡（Back Propagation）發展得最為成熟。BP神經網絡有很多優點。當隱含層或神經元的個數足夠多時，可以逼近任何非線性模型；網絡權值進行求解通過以全局逼近的方式，信息分布在神經元與神經元之間的網絡權值之中，所以BP網絡具有較好的魯棒性和容錯性[4]。

BP神經網絡實質上是一個單向傳播的多層前向反饋網絡，其結構如圖2所示。主要包括三個部分：輸入層、隱含層及輸出層。BP神經網絡的學習由信號的正向傳播和誤差的反向兩部分構成，如圖3所示。當實際輸出值與期望值相差比較大時，要計算其具體的誤差變化，通過利用梯度下降法不斷修改各層神經元的權值與閾值直至誤差信號達到期望的目標為止。

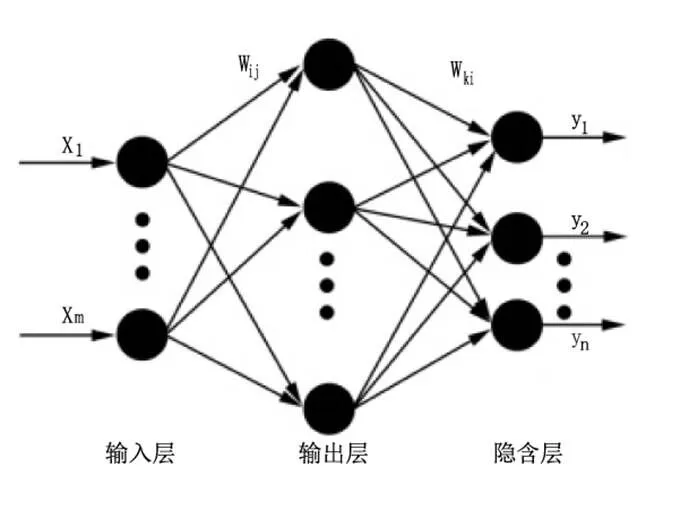
圖2 多層前饋網絡結構圖

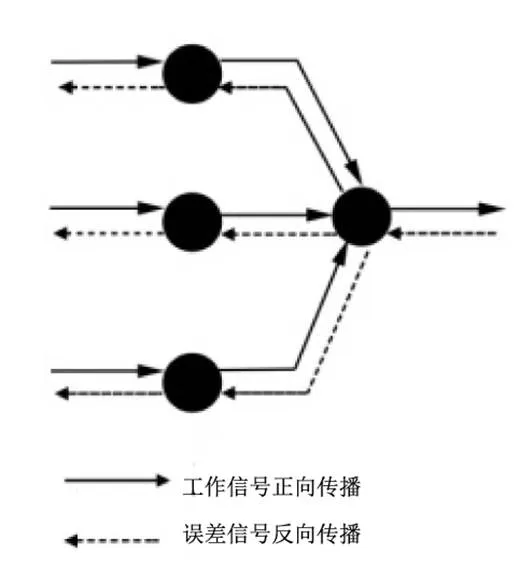
圖3 BP神經網絡學習過程圖

3 逆運動學求解仿真

3.1 求解思路

本文提出了一種結合BP來求解機械手逆運動學問題，從而將機械手逆運動學問題轉化為訓練神經網絡權值及閾值的問題。

針對PUMA560機械手，所謂的逆運動學問題就是在已知機械手末端執行器位姿0A6的條件下，如何求解各關節變量θ1 、θ2 、θ3 、θ4、θ5、θ6。由于0A6的第四行的四個元素為常數，因此選擇其余的12個元素作為整個網絡的輸入，輸入向量為q=[nx ny nz ox oy oz ax ay az Px Py Pz]，6個關節角作為整個神經網絡的輸出，輸出向量為Z=[θ1 θ2 θ3 θ4 θ5 θ6][5]。

BP神經網絡隱含層節點選取至關重要，節點數目太少，網絡不能訓練，節點數目太多網絡的泛化能力也會下降。對機械手逆運動學進行求解的步驟為：（1）產生數據樣本集；（2）網絡的初始化；（3）選取訓練樣本和測試樣本。（4）利用訓練樣本對并行神經網絡進行訓練；（5）網絡訓練結束后，使用測試樣本對整個并行網絡進行測試，將網絡中誤差最小的那組關節角輸出作為整個網絡最終的輸出[6]。

3.2 仿真分析

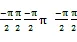
表1 訓練對比表

4 總結

仿真實驗結果表明，本文提出的基于神經網絡的機械手逆運動學求解方法簡單實用，訓練后的并行神經網絡收斂速度快，求解精度高，能夠滿足機械手實時控制中對高速求解逆運動學問題的要求，克服了傳統逆運動學求解方法計算量大、精度低、收斂速度慢等諸多缺陷，為機械手逆運動學求解問題提供了一種新的解決方案。

[1]錢慶文.基于STM32的類人機器人控制系統的研究[D].哈爾濱：哈爾濱理工大學，2014.

[2]王亮.搬運機械手運動控制的研究[D].太原：太原科技大學，2012.

[3]周剛.垂直關節型6自由度機器人笛卡爾空間軌跡規劃的研究[D].廣州：華南理工大學，2011.

[4]林仕高.搬運機器人笛卡爾空間軌跡規劃研究[D].廣州：華南理工大學，2013.

[5]王秋玥，方明.基于多空間混合約束的NAO機器人抓取軌跡規劃[J].長春理工大學學報（自然科學版），2014（6）：107-110.

[6]王濤.基于Matlab仿真的機器手臂笛卡爾軌跡規劃[J].湖南文理學院學報（自然科學版），2015（4）：20-24.

[7]黎柏春，楊建宇，耿磊，等.基于實時逆運動學算法的6R機器人三維仿真[J].組合機床與自動化加工技術，2014（3）：45-48.

[8]王凱凱，萬衡.機器手臂軌跡規劃[J].制造業自動化，2015（13）：8-11.

The Application of Neural Network in the Trajectory Planning of Mechanical Arm

Tang Ruihua

Chaohu College, Anhui Chaohu 238000

The paper introduces the theoretical basis of kinematics of manipulator and the forward kinematics simulation in MATLAB, and verifies the rationality and validity of the model. Then, it focuses on the inverse and tracking of the neural network to realize the basic trajectory, and the training test is conducted on the random Angle of the joint Angle, and the result is good.

neural network; mechanical arm; trajectory planning

TP241；TP183

A

1009-6434（2017）10-0014-03

唐瑞華（1971—），女，漢族，重慶人，巢湖學院講師，物理學碩士，主要研究方向為計算物理和材料物理。