非線性需求下四寡頭價格博弈模型及其復雜特性

劉 峰,李亞光*,王宏興

(1.合肥工業大學經濟學院,安徽合肥230601; 2.合肥工業大學工業信息研究院,安徽合肥230601; 3.淮南師范學院金融學院,安徽淮南232038)

非線性需求下四寡頭價格博弈模型及其復雜特性

劉 峰1,2,李亞光1,2*,王宏興3

(1.合肥工業大學經濟學院,安徽合肥230601; 2.合肥工業大學工業信息研究院,安徽合肥230601; 3.淮南師范學院金融學院,安徽淮南232038)

針對實際競爭環境,建立寡頭廠商成本相異和廣義非線性需求的四寡頭價格博弈模型.基于廠商采用不同決策規則的假設,利用復雜動力學原理,給出了價格博弈模型納什均衡解.研究了系統穩定、倍周期分叉以及混沌的復雜特性,探討了價格調整速度和初始條件對該離散系統動態演化過程的影響,以此為基礎研究了寡頭廠商的價格決策.研究結果表明,寡頭廠商都應采用較低的價格調整速度,慎重選擇博弈的初始條件.當現任寡頭廠商迅速調整價格阻止新廠商進入,使得市場陷入混亂時,運用反饋控制方法可實現混沌控制.

價格博弈;非線性需求;復雜性;不同價格決策;混沌控制

1 引 言

隨著經濟不斷發展,在保險、電力、房地產、通信以及能源等行業中,市場往往被幾個寡頭廠商占領,寡頭壟斷成為一種普遍存在的市場形態.法國經濟學家Bertrand在Cournot雙寡頭壟斷模型基礎上提出了以價格作為競爭手段的Bertrand模型.Bertrand模型假設消費者會選擇價格較低的產品,寡頭廠商會通過不斷降價來爭取更多的顧客;同時每個寡頭廠商希望所獲利潤盡可能大,相互削價直至廠商的價格等于各自的邊際成本.Agiza等[1-3]通過對三寡頭動態博弈的時間演化的離散動態系統進行建模,考慮有限理性的因素,對多寡頭博弈模型穩定性區域做了研究,結果表明混沌現象存在.同時,現實廠商博弈這一問題也引起了學者們的關注.Ahmed等[4]構建廣告競爭模型,根據Lyapunov指數的變化分析復雜動力學行為;賴純見等[5]通過對房地產寡頭完全靜態博弈分析,得出現實中納什均衡可在有限理性不完全信息動態重復博弈下實現的結論;李榆等[6]運用納什協商模型分析了電信運營商和服務提供商的博弈.在研究廠商博弈這一問題的過程中,探討了廠商的生產成本和決策規則.現實中各寡頭廠商的生產成本是不相同的,Bisch等[7,8]對具有線性成本函數的雙寡頭博弈模型進行研究;張驥驤等[9]指出寡頭廠商不局限于線性且結構相同的成本函數,存在不同結構成本函數的雙寡頭博弈情況;易余胤等[10]提出非線性成本函數下雙寡頭重復博弈模型;在多組博弈中,陳曙等[11]將非線性成本函數引入到模型中,建立了基于有限理性的多組動態Cournot模型.當寡頭廠商不再采用單一有限理性的決策規則,而是采用不同的決策規則時,潘玉榮等[12]提出不同理性雙寡頭博弈模型;方志耕等[13]構建了一種具有普遍適用性的描述性博弈結構模型;馬軍海等[14]采用延遲有限理性預期規則研究三寡頭價格博弈模型的穩定性以及分岔、混沌等復雜性態.

文獻[15–19]對價格博弈模型的穩定性以及分岔、混沌的影響因素進行了研究.Ma等[15,16]分別建立基于有限理性的混合雙寡頭模型和不同決策規則下的三寡頭模型,發現價格調整速度變化會導致混沌,但是混沌控制策略使得市場有序競爭.Elsadany[17]指出當雙寡頭Cournot模型的反需求函數為非線性函數時,參數的變化也會引起混沌現象.從現有研究結果可看出,眾多行業領域的市場結構呈現出采用價格競爭的四寡頭壟斷廠商的形式.馬軍海等[18]基于延遲有限理性決策,研究了中國啤酒市場線性需求的四寡頭價格博弈模型,分析了系統的穩定性.Zhang等[19]構建中國保險市場的四維離散動態系統,研究表明在線性需求條件下,系統對價格調整速度和初始條件的敏感依賴.

文獻[18,19]基于四維復雜離散動態模型探討四寡頭壟斷廠商的內在復雜性,并對其進行混沌控制研究,說明四寡頭壟斷廠商在現實經濟中普遍存在.但是當前在研究四寡頭廠商行為時,所假設的需求函數是線性的,而現實中很多情況下需求函數是比較復雜的,非線性函數往往能夠更準確的描述市場需求關系.同時在實際經濟環境中,寡頭廠商并不局限于結構相同的成本函數[7-11],寡頭間或存在相異成本.本文在考慮寡頭間存在相異成本、非線性市場需求函數的基礎上,建立四寡頭價格博弈模型,并探討價格調整速度對寡頭廠商利潤的影響,以及價格博弈動力系統對初始條件的敏感依賴;同時利用MATLAB進行數值仿真,分析系統的復雜特性;最后使用延遲反饋控制法[20-22]控制混沌現象,其結果對中國石油行業可能存在的四寡頭壟斷市場管理決策提供理論依據.

2 價格博弈模型

在一定的預算約束下實現效用最大化時,可得出廠商的需求函數,效用函數的形式決定了需求函數的形式.新進寡頭廠商可能由于創新技術與市場決策等因素,導致其產品相較與原寡頭廠商存在顯著差異,消費者更偏好此類產品,故需求函數形式不同.實際上,各廠商的生產成本也是不相同的,同類廠商的生產成本非常相近,而異類廠商的生產成本存在差異.為了研究問題的方便,在建立價格博弈模型時,給出以下假設:

1)市場上已有三個生產可替代產品的寡頭廠商1,2,3,一個新進寡頭廠商4進入市場,成為市場中新的強有力競爭者;

2)寡頭廠商1,2,3的需求量與價格的關系滿足二次多項式形式,即其需求函數是二次多項式;

3)原寡頭廠商1,2,3屬于同類寡頭,其需求無顯著差異,而新進寡頭廠商4屬于異類寡頭,與原寡頭廠商1,2,3相比,其需求存在較明顯的差異,寡頭廠商4的需求函數是線性的1例如,目前中國有中國石油天然氣股份有限公司、中國石油化工集團公司和中國海洋石油總公司三大石油行業油氣生產和銷售廠商,隨著國家市場經濟的進一步深化,可能會有新的生產和銷售廠商進入,這樣就會形成四寡頭競爭的新格局.在一般情況下,商品價格上升,需求量就會下降.因此需求函數是一個關于價格的單調減函數.同時,需求函數不是固定不變的,它會隨著市場變化而變化.文獻[18,19]假定需求函數是線性的,而文獻[16]假定需求函數是非線性的.本文假定原寡頭廠商1,2,3的需求函數為非線性函數,寡頭廠商4的需求函數為線性函數.;

4)寡頭廠商1,2,3的產品成本是關于需求量的函數,而需求量又是關于價格的函數,故寡頭廠商1,2,3的成本是關于價格的函數,即一定區域、一定時期內產品成本僅由廠商市場價格決定,不受其它因素的影響;

5)寡頭廠商4的成本與需求量呈正相關,成本函數是線性的.

一個寡頭廠商不僅影響自己的決策,而且影響其他寡頭廠商的決策,甚至改變整個市場的運行狀態.根據假設2)和3),第t期寡頭廠商1,2,3的非線性需求函數可設為

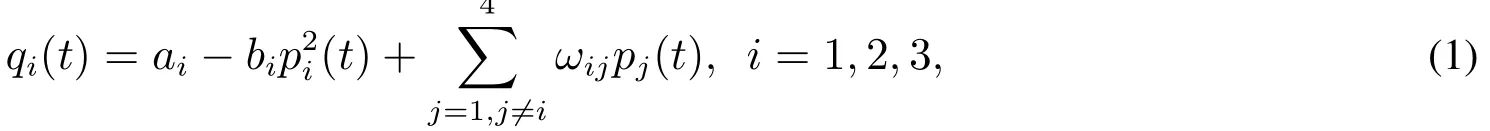
其中bi是需求對自身價格的彈性系數,ai,ωij,i/=j,j=1,2,3,4,為各寡頭產品的相互替代率,pi和qi分別是第i個廠商的銷售價格和需求量,i=1,2,3.

由假設4),可設成本函數形式為cipi(t),其中ci為廠商技術水平對價格的敏感系數,i=1,2,3.則寡頭廠商1,2,3的利潤函數表達式為

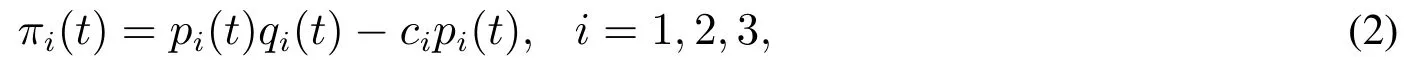
整理可得

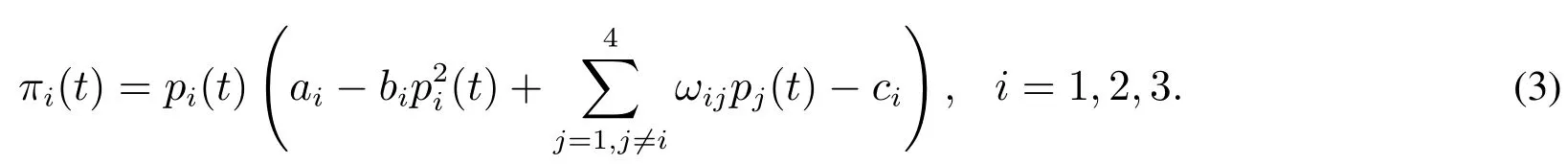
新進寡頭廠商和原寡頭廠商生產的產品不完全同質,價格需求關系不同,需求函數結構存在差異.新進寡頭廠商生產的產品比原寡頭廠商的可替代性差,即使銷售價格稍高,由于品牌效應、產品高品質與先進技術,仍然會有相對較高的需求.根據假設3),寡頭廠商4的需求函數可設為

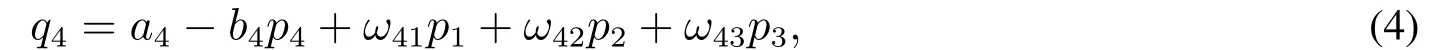
根據假設5),成本函數為c4q4(t),其中c4為單位產量的成本,則利潤函數

2.1 四寡頭價格博弈模型

由于寡頭壟斷市場信息的不完全性,每個廠商掌握的信息并不充分,只可能做出有限理性決策.考慮到廠商1,2,3是先進廠商,管理市場的經驗比較豐富、處理市場信息能力比較強,采用有限理性決策規則[9,10,13,15].由于廠商4是新進廠商,往往只能是簡單理性的,不具有足夠的價格調整能力,故選擇根據邊際利潤為零的最優反應價格決策原則.

在現實中廠商之間的博弈是一個動態過程,具有適應性和長程記憶性等特征,所以不妨假設廠商1,2,3采用有限理性決策規則,即第t+1期的價格決策由其第t期的價格與邊際利潤加權決定.廠商1,2,3采用有限理性決策規則進行決策,也就是說如果邊際利潤為正,需求量將在下一期增加,反之,則會減少.αi,i=1,2,3為價格調整速度,價格調整過程為

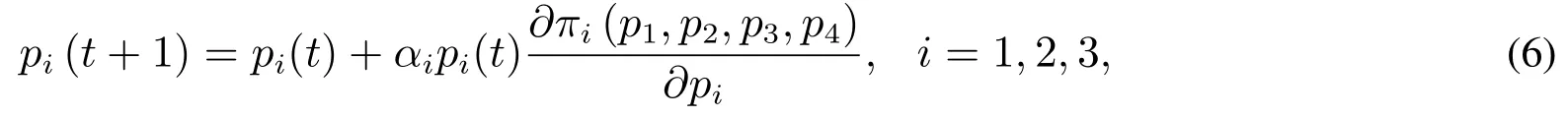
其中pi(t+1)和pi(t)分別是第t+1期和第t期的價格.在第t期,原寡頭廠商的邊際利潤函數為

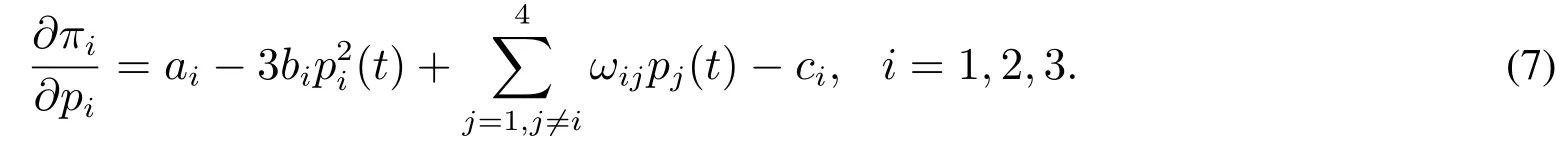
新進寡頭廠商4在大部分情況下不完全了解市場信息,沒有足夠的價格調整能力,為了追求利潤最大化,按照自身的邊際利潤來調整價格,選擇根據自身邊際利潤的最優反應價格決策原則,即其下期的價格是基于本期對其他廠商價格的最優反應.現期價格僅僅通過第t期的最優價格決策決定,當

時,可得

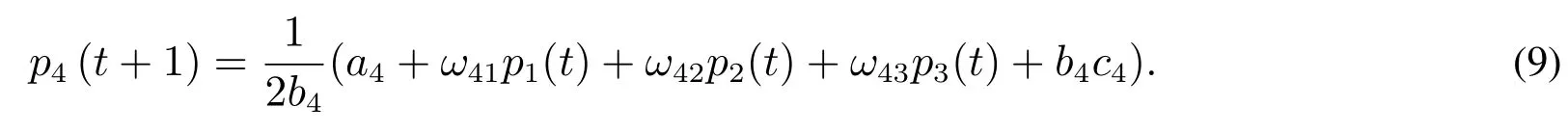
所以四個寡頭廠商根據不同決策規則,形成的價格博弈離散動力學系統為

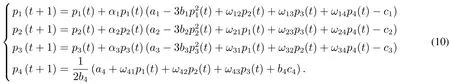
2.2 模型分析

根據四個寡頭廠商建立的價格博弈離散動力學系統(10),研究其納什均衡的局部穩定性,進而研究其博弈過程.令pi(t+1)=pi(t),i=1,2,3,4,求得系統平衡點.

為了討論離散動力學系統(10)的穩定性,考慮其Jacobi矩陣為

系統(10)的特征多項式為

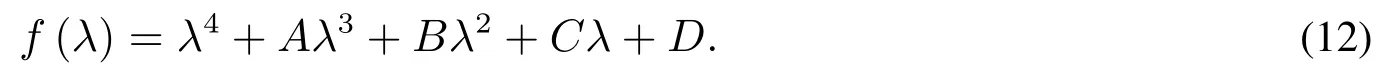
平衡點局部穩定的Jury條件是

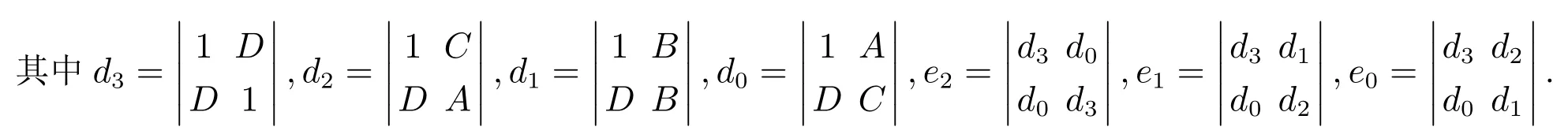
從經濟管理學的角度看,系統的納什均衡點比邊界平衡點更具有現實意義,在該點處四個廠商的產量均不為0.通過計算特征值來判斷納什均衡點的穩定性很難,可以用Jury條件來判斷納什均衡點的穩定性,根據Jury條件得出的廠商價格調整速度α1,α2,α3的范圍.在現實中,寡頭廠商保證價格調整速度αi,i=1,2,3在此范圍內,經過博弈將逐漸穩定到納什均衡點,避免由于價格的過度調整引起市場混亂、利潤降低.寡頭企業管理者為了維持市場穩定,避免利潤降低,更愿意保持在納什均衡狀態.

3 數值模擬分析

αi,i=1,2,3是可控參數,取下列參數值研究系統的均衡點及穩定性.對于四個寡頭廠商的相互替代率ai,i=1,2,3,4,異類寡頭4與原寡頭廠商相比,產品差異性更大,對市場的操縱能力更強,產品可替代性較低,故設定需求函數中相互替代率a4相對較小.因為原寡頭廠商的技術水平類似,設定考慮廠商技術水平條件下對價格的敏感系數ci,i=1,2,3較為接近,且均比新進廠商單位成本c4高.各寡頭產品的相互替代率ωij參考中國保險市場數據[19],均設定在0和1之間,即

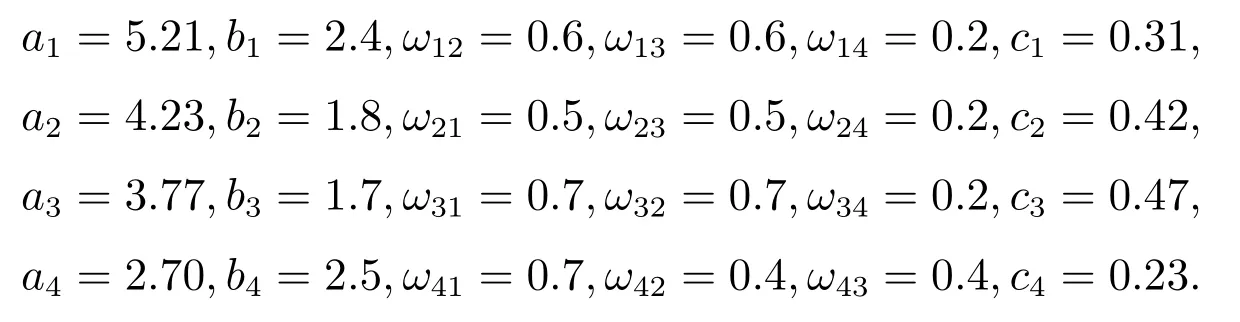
令pi(t+1)=pi(t),i=1,2,3,4,求得系統(10)平衡點

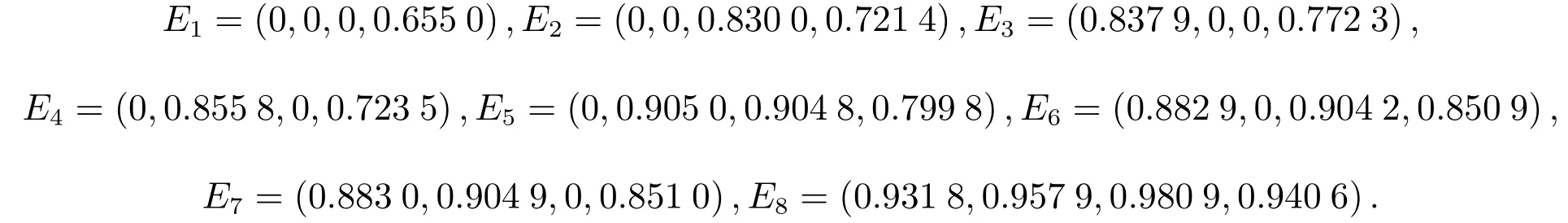
根據Jacobi矩陣J,求出每一點對應的特征值.有界均衡點E1,E2,E3,E4,E5,E6,E7的非零特征值均大于1,均是不穩定均衡點.E8的非零特征值均小于1,是系統(10)唯一的納什均衡點.

考慮上述參數值時,納什均衡點為E8=(0.931 8,0.957 9,0.980 9,0.940 6),Jacobi矩陣為

系統(10)的特征多項式

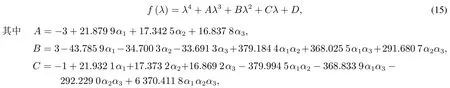
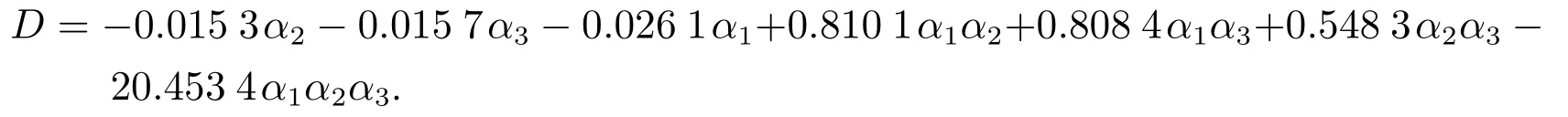
用納什均衡點的Jury條件(13)驗證可控參數αi,i=1,2,3的取值.當價格調整速度αi,i=1,2,3取值在一定范圍內時,無論壟斷廠商1,2,3最初如何定價,四個壟斷廠商在納什均衡點均會達到穩定.當價格調整速度αi,i=1,2,3取值超出一定范圍,系統(10)納什均衡點E8的穩定狀態將會被打破,先出現分叉,隨后出現混沌.

3.1 分叉與混沌仿真

根據Jury條件選取α2=0.07,α3=0.11時,得到四個寡頭廠商隨著α1變化的價格分叉圖1;選取α1=0.12,α3=0.11時,得到四個寡頭廠商隨著α2變化的價格分叉圖2;選取α1=0.12,α2=0.11時,得到四個寡頭廠商隨著α3變化的價格分叉圖3.

圖1,圖2和圖3分別出現了穩定周期、倍周期分叉以及混沌狀態,隨著α1,α2和α3的變化,價格也呈現動態變化過程.當α1,α2和α3達到某個臨界點時,系統(10)由穩定狀態變為分叉,再由分叉變為混沌.

根據判斷系統狀態的最大Lyapunov指數,得到系統最大Lyapunov指數變化圖4,圖5和圖6.αi,i= 1,2,3不同,最大Lyapunov指數不同,穩定狀態時Lyapunov指數小于0,混沌狀態時大于0.

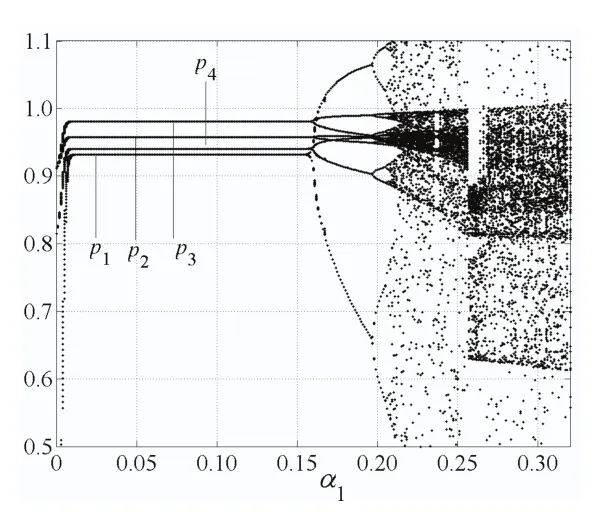
圖1 α2=0.07,α3=0.11,α1變化的價格分叉圖Fig.1 The price bifurcation with change of α1when α2=0.07,α3=0.11

圖2 α1=0.12,α3=0.11,α2變化的價格分叉圖Fig.2 The price bifurcation with change of α2when α1=0.12,α3=0.11

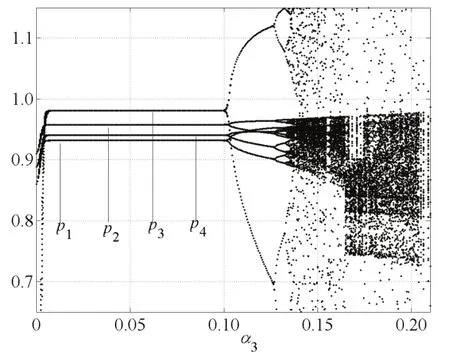
圖3 α1=0.12,α2=0.11,α3變化的價格分叉圖Fig.3 The price bifurcation with change of α3when α1=0.12,α2=0.11

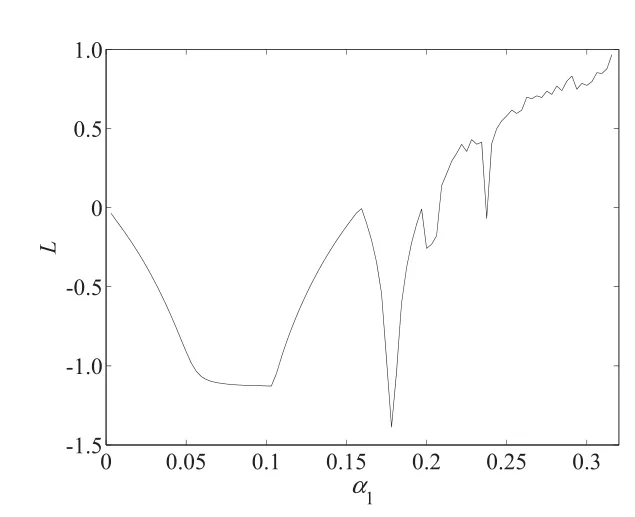
圖4 當α2=0.07,α3=0.11時,α1的系統最大Lyapunov指數(L)動態變化圖Fig.4 Change of the maximal Lyapunov exponent with α1when α2=0.07,α3=0.11

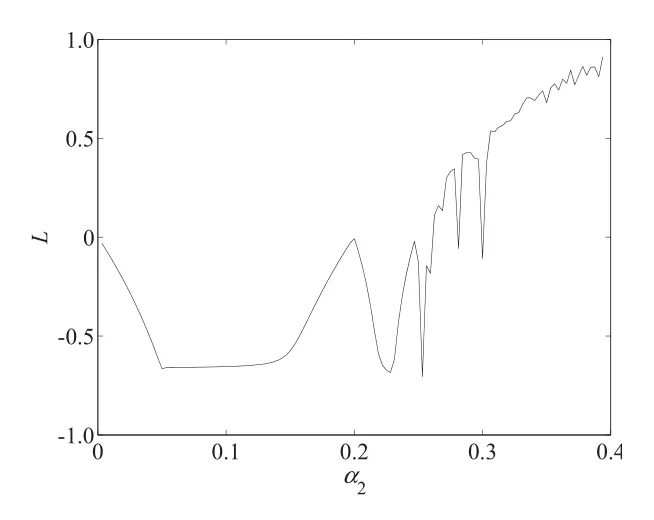
圖5 當α1=0.12,α3=0.11時,α2的系統最大Lyapunov指數(L)動態變化圖Fig.5 Change of the maximal Lyapunov exponent with α2when α1=0.12,α3=0.11

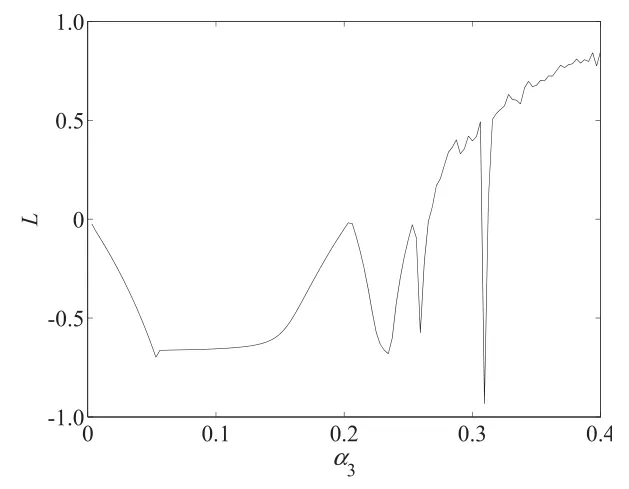
圖6 當α1=0.12,α2=0.11時,α3的系統最大Lyapunov指數(L)動態變化圖Fig.6 Change of the maximal Lyapunov exponent with α3when α1=0.12,α2=0.11

當α2=0.07,α3=0.11時,壟斷廠商1的價格調整速度α1為變量.由圖1,圖4知,當0＜α1＜0.155時,Lyapunov指數小于0,此時系統(10)為穩定狀態;當α1=0.155時,系統(10)出現第一次分叉,Lyapunov指數等于0;當α1=0.198時,系統出現第二次分叉,Lyapunov指數等于0,則0.155＜α1＜ 0.198是周期2軌道分叉區域;當α1=0.209時,系統出現第四次分叉,Lyapunov指數等于0,則0.198＜α1＜0.209是周期4軌道分叉區域;當α1＞0.209時,系統進入混沌狀態,Lyapunov指數大于0,進一步價格調整將引起市場混亂.在分叉圖的空白區域,α1=0.254附近Lyapunov指數小于0.

由圖2和圖5知,當α1=0.12,α3=0.11時,隨著α2變化,當α2=0.197時,系統出現倍周期分叉;α2＞0.268時,系統進入混沌狀態.由圖3和圖6知,當α1=0.12,α2=0.11時,隨著α3變化,當α2=0.202時,系統出現倍周期分叉;當α1＞0.273時,系統進入混沌狀態,進一步價格調整將引起市場混亂.

混沌發生時市場陷入混亂無序狀態,無論是廠商自身還是其競爭對手都會受到傷害.各寡頭廠商管理者盡力控制價格調整速度,避免因價格戰所帶來的市場混亂.復雜動力系統的混沌研究為宏觀調控提供一定依據.

3.2 初值條件影響系統動態演化過程

當α1=0.31,α2=0.32,α3=0.35時系統處于混沌狀態.從納什均衡點E8開始,價格隨時間無序變化.為了探究初始條件的變化對系統演化的混沌狀態的影響,在圖7中分別以納什均衡點E8= (0.931 8,0957 9,0.980 9,0.940 6)為初始值和相對E8有微小變動的初始值Fi畫出了寡頭廠商i的產品價格pi隨時間變化的曲線,i=1,2,3,4.與四個寡頭廠商相應的Fi(加下劃線的數據表示相對E8有微小變動)取值如下:

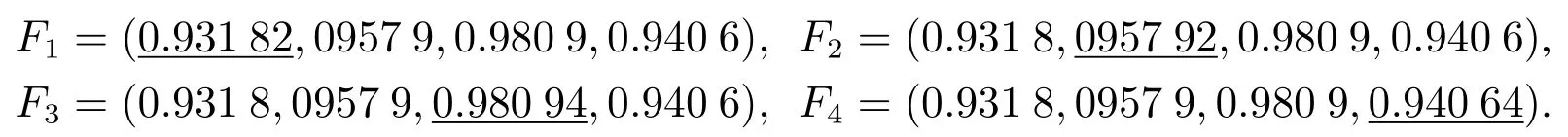
圖7 初始條件變化時,四寡頭廠商價格隨時間變化對比圖Fig.7 Price difference changes of four oligarchs with time when initial conditions change

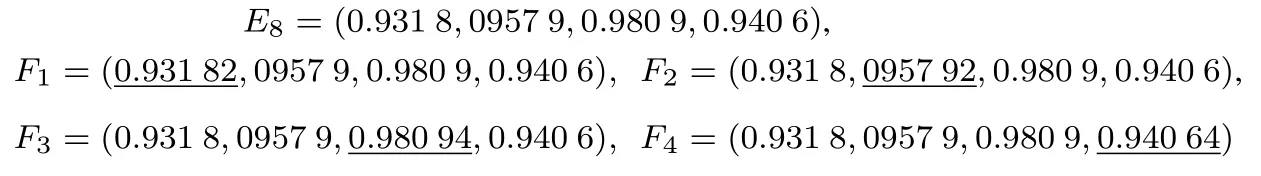
圖7表明,與E8,Fi對應的兩條曲線在系統動態演化的前期均是無序狀態且無顯著差別,但隨著時間增加,價格變動軌跡的區別越來越明顯.以均衡點E8為初值的價格隨時間變化較為平穩,振蕩幅度較小,而以Fi為初值的價格變化軌跡卻有較大幅度的振蕩.由此可知系統動態演化過程的混沌現象對初始條件變化較敏感.

3.3 價格調整速度影響利潤

圖8,圖9和圖10是α1,α2,α3變化時的利潤分叉圖.α1,α2,α3選取與分叉圖相同的參數,四個寡頭廠商利潤分岔圖中的穩定、周期2軌道分叉、周期4軌道分叉和混沌區域與圖1,圖2,圖3的價格分叉圖中出現的穩定周期、倍周期分叉以及混沌區域相同.

同理,α2,α3的變化對廠商2,3的利潤具有類似的影響.

由圖11知,當價格調整速度α1較小,廠商利潤不斷增加,直至Lyapunov指數為0,利潤開始下降,這也得出價格調整速度不能過快的結論.由圖8,圖11可以看出,當0＜α1＜0.155時,系統處于穩定狀態,四寡頭廠商的利潤平穩變化;當0.155＜α1＜0.198時,系統處于倍周期分叉狀態,四寡頭廠商的利潤下降;當0.198＜α1＜0.209時,系統處于四倍周期分叉狀態,四寡頭廠商的利潤繼續下降;當α1＞0.209時,系統處于混沌狀態,四寡頭廠商的利潤較低.在相同參數條件下,四個寡頭廠商的利潤分岔圖與價格分叉圖比較,發現系統的穩定周期、倍周期分叉以及混沌狀態相同,由此得出價格調整速度對于價格與利潤產生一樣的影響.所以,寡頭企業管理者可以僅僅根據價格分叉圖來盡力避免分叉、混沌現象的產生,以確保利潤最大化.

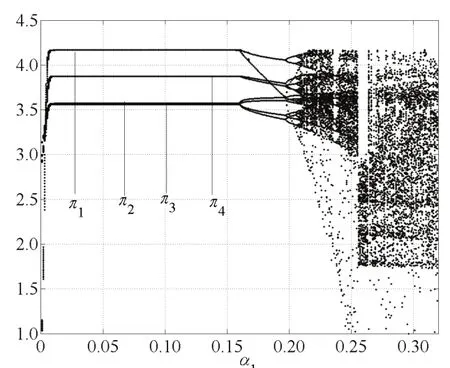
圖8 α2=0.07,α3=0.11,α1變化的利潤分叉圖Fig.8 The proft bifurcation with change of α1when α2=0.07,α3=0.11

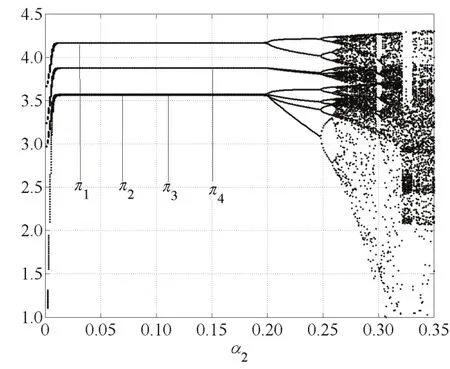
圖9 α1=0.12,α3=0.11,α2變化的利潤分叉圖Fig.9 The proft bifurcation with change of α2when α1=0.12,α3=0.11

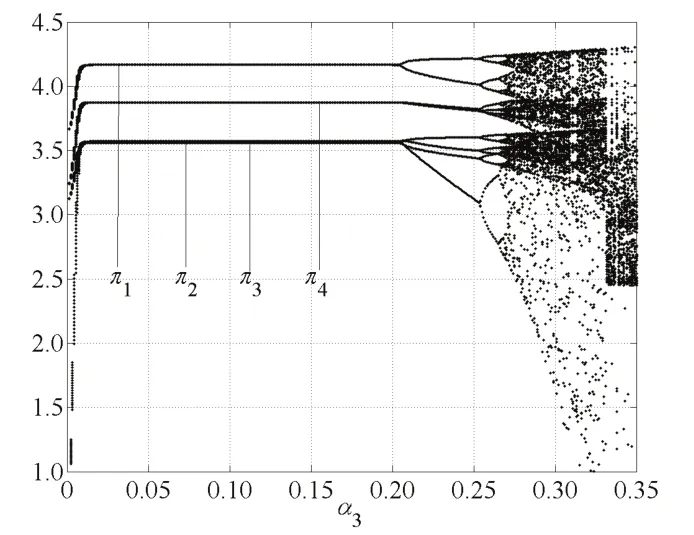
圖10 α1=0.12,α2=0.11,α3變化的利潤分叉圖Fig.10 The proft bifurcation with change of α3when α1=0.12,α2=0.11

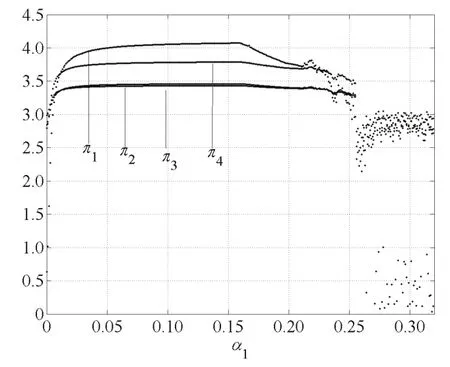
圖11 α1變化時利潤圖Fig.11 The proft with the change of α1

4 混沌控制

一般情況下,現任寡頭廠商為阻止新廠商進入市場會采取價格戰,而迅速調整的價格使市場陷入混沌狀態中.并且參數的微小變化可能會使得系統由穩定狀態陷入混沌.所以,現任寡頭廠商1,2,3與新進寡頭廠商4的市場穩定狀態可能是暫時和短期的.當市場處于混沌狀態時,每個廠商的價格是不確定的,廠商無法實現最大化利潤.因此每個廠商都希望控制混沌現象,促使穩定狀態的形成.

本文使用延遲反饋控制法[14,17,18]控制混沌,依據系統的具體參數取值,只有原廠商1,2,3引入延遲變量[14],才可以達到理想效果,故采用此方法對系統(10)實施控制.控制系統如下

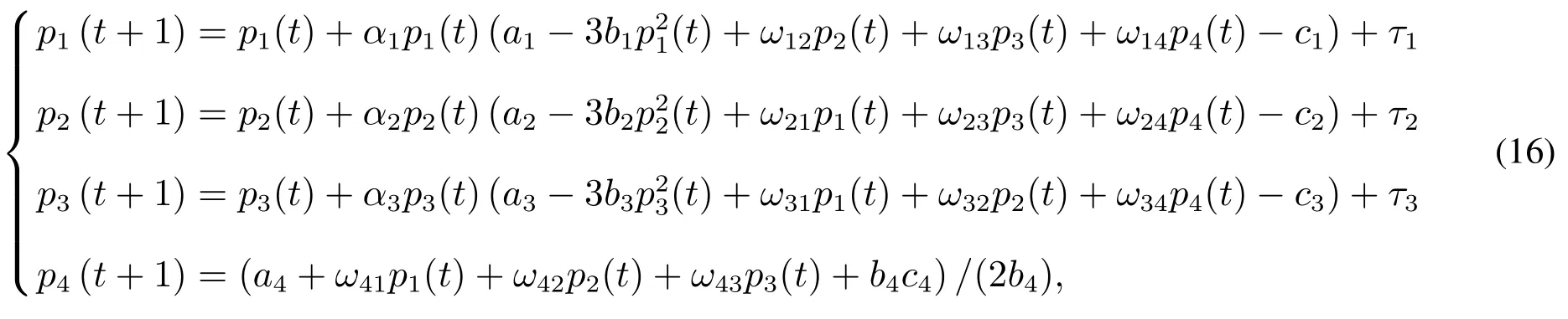
其中控制信號為τi=K(pi(t+1-T)-pi(t+1)),i=1,2,3,控制因子為K,輸出信號延遲時間長度為T,取T=1.

圖12描述了控制因子K對價格的影響.圖12表明,當0＜K＜0.504時,系統處于混沌狀態;當0.504＜K＜0.576時,系統處于周期4軌道分叉狀態;當0.576＜K＜0.892時,系統處于周期2軌道分叉狀態;當K＞0.892時,系統處于穩定狀態,控制了混沌,廠商可以實現利潤最大化.

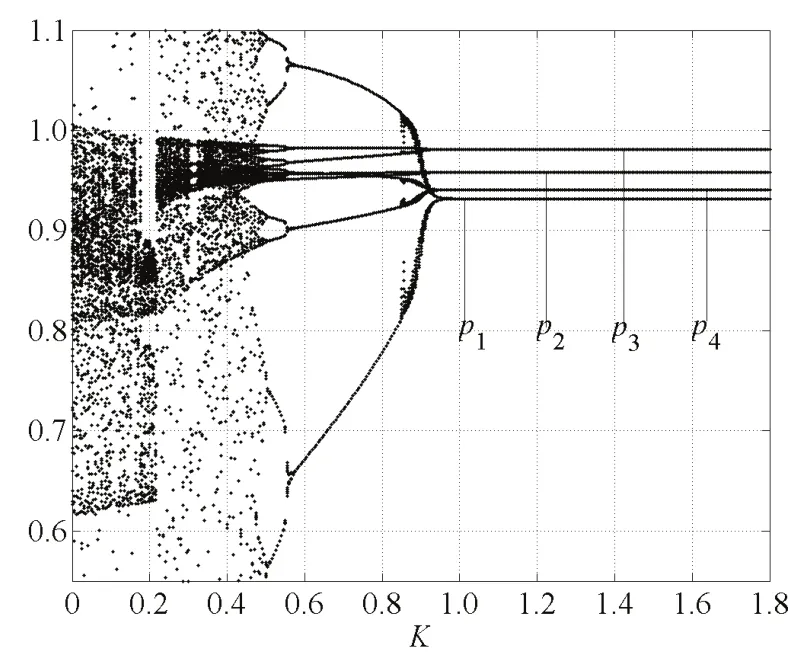
圖12 控制因子K對價格的影響Fig.12 The infuence of K on the price

5 結束語

當一個新寡頭廠商進入三個寡頭廠商占領的市場時,通過對不同決策規則下具有相異成本和非線性需求函數的寡頭廠商價格博弈過程的分析,提出了一個新的四維離散動力學系統,建立了四寡頭價格博弈模型.寡頭廠商為了追求自身利益最大化,會不斷加快自己的價格調整速度,忽視其對整個市場的外部效應,數值模擬結果表明,一旦價格調整速度超出穩定范圍會使整個市場陷入混沌,此時自身利潤反而降低.無論是新進入的寡頭廠商還是現任寡頭廠商,基于利益最大化的目的都應采用較低的價格調整速度.當市場中寡頭廠商價格調整速度過快時,會出現分叉甚至混沌的不和諧現象,政府應及時出臺相關政策來調控市場,使市場健康有序的發展.

所有寡頭廠商初始狀態的微小差別都會對博弈結果產生極大影響,為使市場處于穩定狀態,寡頭廠商應慎重選擇博弈的初始條件.市場陷入混亂時,寡頭廠商可采用延遲反饋控制法控制混沌,達到搶占更多市場份額并且擠壓對手的生存發展空間的目的.本文在建立博弈模型時,假定廠商銷售量只與價格有關系,實際上影響銷售量的因素很多,例如產品質量、市場需求等,這些問題有待進一步分析研究.

參考文獻:

[1]Agiza H N,Bischi G I,Kopel M.Multistability in a dynamic Cournot game with three oligopolists.Mathematics and Computers in Simulation,1999,51(1/2):63–90.

[2]Agiza H N,Hegazi A S,Elsadany A A.The dynamics of Bowley’s model with bounded rationality.Chaos,Solitons&Fractals, 2001,12(9):1705–1717.

[3]Agiza H N,Elsadany A A.Chaotic dynamics in nonlinear duopoly game with heterogeneous players.Chaos,Solitons&Fractals, 2004,149(3):843–860.

[4]Ahmed E,Agiza H N,Hassan S Z.On modelling advertisement in Cournot duopoly.Chaos,Solitons&Fractals,1999,10(7): 1179–1184.

[5]賴純見,陳 迅.房地產寡頭有限理性博弈模型的復雜性分析.系統工程學報,2013,28(3):285–296. Lai C J,Chen X.Analysis of a game with bounded rationality in oligopoly market.Journal of Systems Engineering,2013,28(3): 285–296.(in Chinese)

[6]李 榆,吳軍口,馮艷剛.基于Nash協商模型的電信增值服務供應鏈研.系統工程學報,2014,29(6):824–832. Li Y,Wu J K,Feng Y G.Research on telecom value-added service chain based on Nash bargaining model.Journal of Systems Engineering,2014,29(6):824–832.(in Chinese)

[7]Bischi G I,KopelM,HassanS Z.Equilibrium selection in anonlinearduopoly gamewith adaptiveexpectations.JournalofEconomic Behavior&Organization,2001,46(1):73–100.

[8]Bischi G I,Mammana C,Gardini L.Multistability and cyclic attractors in duopoly games.Chaos,Solitons&Fractals,2000,11(4): 543–564.

[9]張驥驤,達慶利,王延華.寡占市場中有限理性博弈模型分析.中國管理科學,2006,14(5):109–113. Zhang J X,Da Q L,Wang Y H.Analysis of a game with bounded rationality in oligopoly market.Chinese Journal of Management Science,2006,14(5):109–113.(in Chinese)

[10]易余胤,盛昭瀚,肖條軍.具溢出效應的有限理性雙寡頭博弈的動態演化.系統工程學報,2004,19(3):244–250. Yi Y Y,Sheng Z H,Xiao T J.Dynamics of duopoly model with bounded rationality and spillover effect.Journal of Systems Engineering,2007,4(2):71–76.(in Chinese)

[11]陳 曙,姚洪興.多組動態古諾模型的穩定性分析.復雜系統與復雜性科學,2006,3(3):48–55. Chen S,Yao H X.Stability analysis for a dynamical multi-team Cournot game.Journal of Systems Engineering,2006,3(3):48–55. (in Chinese)

[12]潘玉榮,賈朝勇.不同理性雙寡頭博弈模型的復雜性分析.復雜系統與復雜性科學,2007,4(2):71–76. Pan Y R,Jia C Y.Complex dynamics analysis for a duopoly game with heterogeneous plyers.Complex Systems and Complexity Science,2007,4(2):71–76.(in Chinese)

[13]方志耕,劉思峰,李元年,等.基于有限知識和理性的雙寡頭戰略定產納什均衡問題研究.中國管理科學,2006,14(5):114–120. Fang Z G,Liu S F,Li Y N,et al.Study on the Nash equilibrium of duopoly strategy output-making based on bounded knowledge and bounded rationality.Chinese Journal of Management Science,2006,14(5):114–120.(in Chinese)

[14]馬軍海,彭 靖.延遲決策對一類寡頭博弈模型的影響分析.系統工程學報,2010,25(6):812–817. MA J H,Peng J.Infuence of delayed decision on an oligopoly game model.Journal of Systems Engineering,2010,25(6):812–817. (in Chinese)

[15]Ma J,Pu X.The research on Cournot-Bertrand duopoly model with heterogeneous goods and its complex characteristics.Nonlinear Dynamics,2013,72(4):895–903.

[16]Ma J,Sun Z.The research on price game model and its complex characteristics of triopoly in different decision-making rule. Nonlinear Dynamics,2013,71(1/2):35–53.

[17]Elsadany A A.A dynamic Cournot duopoly model with different strategies.Journal of the Egyptian Mathematical Society,doi: 10.1016/j.joems.2014.01.006.

[18]馬軍海,吳可菲.中國啤酒市場的四寡頭價格博弈及其延遲決策.系統工程學報,2013,28(6):717–728. Ma J H,Wu K F.Four-oligarchy price game and its delayed decision in Chinese beer market.Journal of Systems Engineering,2013, 28(6):717–728.(in Chinese)

[19]Zhang J,Ma J.Research on the price game model for four oligarchs with different decision rules and its chaos control.Nonlinear Dynamics,2012,70(1):323–334.

[20]Wu W,Chen Z,Ip W H.Complex nonlinear dynamics and controlling chaos in a Cournot duopoly economic model.Nonlinear Analysis:Real World Application,2010,11(5):4363–4377.

[21]張建雄,唐萬生.一類Holder連續的混沌系統分析和控制.系統工程學報,2010,25(6):829–834. Zhang J X,Tang W S.Analysis and control for a class of chaotic systems with Holder continuity.Journal of Systems Engineering, 2010,25(6):829–834.(in Chinese)

[22]Fuh C C,Tsai H H,Yao W H.Combining a feedback linearization controller with a disturbance observer to control a chaotic system under external excitation.Communications in Nonlinear Science&Numerical Simulation,2012,17(3):1423–1429.

Four oligarchs price game model and its complex characteristics with nonlinear demand

Liu Feng1,2,Li Yaguang1,2*,Wang Hongxing3
(1.School of Economics,Hefei University of Technology,Hefei 230601,China; 2.Research Center of Industry Information,Hefei University of Technology,Hefei 230601,China; 3.School of Finance,Huainan Normal University,Huainan 232038,China)

In view of the actual competitive environment a four-oligarch price game model with variable costs and general nonlinear demand is established.Based on the hypothesis that vendors use different decision rules, using complex principle of dynamics the Nash equilibrium solutions are give.This paper studies the complex characteristics such as stability,the period-doubling bifurcation,and chaos.It also discusses the effects of price adjustment speed and initial conditions on the movement of the dynamic system,and the price decisions of oligarchs.The results show that the lower price adjustment speed should be taken,and initial conditions of the game must be chosen carefully.When the current oligarchs quickly adjust price in order to prevent a new oligarch from entering and market into chaos results,the delay feedback control method can be used to control the chaos.

price game;nonlinear demand;complexity;different price decision;chaos control

TP273

A

1000-5781(2016)06-0719-10

10.13383/j.cnki.jse.2016.06.001

劉 峰(1971—),男,安徽天長人,博士生,副教授,碩士生導師,研究方向:區域經濟學,Email:dwoffce@126.com;

2015-02-16;

2015-11-19.

國家自然科學基金資助項目(11401243);中央高校基本科研業務費專項資金資助項目(J2014HGXJ0156);安徽省人文社科重點研究基地資助項目(SK2015A159).

*通信作者

李亞光(1990—),女,安徽淮南人,碩士生,研究方向:區域經濟學,博弈論,Email:yaguangli926@163.com;

王宏興(1981—),男,安徽淮南人,博士,副教授,研究方向:數值計算,Email:winghongxing0902@163.com.