修正型緩坡方程的有限元模型

倪云林，滕斌，叢龍飛

(1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024； 2. 浙江海洋大學 港航與交通運輸工程學院，浙江 舟山 316022)

?

修正型緩坡方程的有限元模型

倪云林1,2，滕斌1*，叢龍飛1

(1.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024； 2. 浙江海洋大學 港航與交通運輸工程學院，浙江 舟山 316022)

與緩坡方程相比，修正型緩坡方程增加了地形曲率項和坡度平方項，從而提高了數值求解的復雜性。本文將計算域劃分為內域和外域，內域為水深變化區域，使用修正型緩坡方程，其中的地形曲率項和坡度平方項可用有限單元各節點的水深信息和單元插值函數表示，外域為水深恒定區，速度勢滿足Helmholtz方程，通過內外域的邊界匹配建立有限元方程，并用高斯消去法求解。進而分別模擬了波浪傳過Homma島和圓形淺灘的變形，其結果與相關的解析解和實驗數據吻合良好，證明了本文有限元模型的正確性。同時，通過與實驗數據的對比也明顯看出，在地形坡度較陡的情況下，修正型緩坡方程較緩坡方程具有更高的計算精度。

修正型緩坡方程；有限元；Homma島；圓形淺灘

1 引言

波浪在由深海向淺水傳播的過程中，受海底地形的影響，會發生淺化、折射、繞射等一系列的變形。為了研究這一過程中波浪要素的變化規律，許多學者建立和改進了各種數學模型。緩坡方程(mild slope equation, MSE)就是其中的一種，通過沿水深積分的方法將三維問題轉化為二維問題，具有方程形式簡單且應用范圍較廣的優點。

緩坡方程最初由Berkhoff(1972年)提出，又稱為折射-繞射聯合模型，是在緩坡假設的基礎上，用線性波浪理論研究緩變、不可滲透地形上波浪的傳播變形問題[1]。關于該方程的使用條件，Booij(1983年)證明緩坡方程在底坡小于1∶3的情況下具有足夠的精度[2]，但在底坡大于1∶3或地形波動的情況下，緩坡方程則不能準確描述波浪的傳播變形。為了改善“緩坡假設”的條件限制，Kirby(1986年)最先對緩坡方程進行了改進，他將劇變地形分解成一個緩變地形和一個小振幅波動地形的疊加，導出了擴展型緩坡方程(extended mild slope equation，EMSE)，提高了地形波動情況下緩坡方程的計算精度[3]。之后，Chamberlain和Porter[4](1995年)，Chandrasekera和Cheung[5](1997年)通過引入地形曲率項和坡度平方項對緩坡方程進行了修正，得到了修正型緩坡方程(modified mild slope equation, MMSE)，提高了陡變地形和劇變地形情況下緩坡方程的計算精度，從而大大拓寬了緩坡方程的應用范圍。

目前，有不少文獻對修正型緩坡方程的求解方法進行了論述。例如，Suh等將修正型緩坡方程轉化為一階雙曲型方程組，采用有限差分法進行求解[6]。Silva等采用中心差分格式離散控制方程和邊界條件來求解修正型緩坡方程[7]。有限差分法具有數學概念直觀、表達簡單、發展成熟等優點，但差分網格通常為矩形，在邊界不規則或形狀復雜時精度降低。因此，本文將采用有限元法直接對修正型緩坡方程進行求解，解決地形曲率項和坡度平方項的空間離散問題。在求解過程中，將整個計算域劃分為內域和外域，內域是水深變化的有限區域，可用有限元離散，外域是水深恒定的無限區域，速度勢滿足Helmholtz方程，其解為級數形式，通過內外域公共邊界上的匹配條件建立并求解有限元方程[8—11]。

2 控制方程

針對水深變化海床上的波浪運動問題，Chamberlain和Porter[4]采用變分原理推導了修正型緩坡方程：

▽·(ccg▽φ)+[k2ccg+f1(kh)g▽2h

+f2(kh)gk(▽h)2]φ=0.

(1)

式中，▽為水平梯度算子；φ為速度勢的空間分量；c和cg分別為波速和群速度；k為波數；h為水深；g為重力加速度；f1(kh)和f2(kh)分別為地形曲率項系數和坡度平方項系數，其表達式如式(2)、(3)所示[5]。

f1(kh)=[-4khcosh(kh)+sinh(3kh)+sinh(kh)

+8(kh)2sinh(kh)]/{8cosh3(kh)[2kh+sinh(2kh)]}

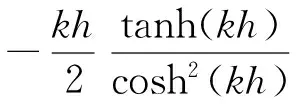
(2)

16(kh)3sinh(2kh)-9sinh2(2kh)cosh(2kh)+

12(kh)[1+2sinh4(kh)][kh+sinh(2kh)]}.

(3)

上述兩個系數均為kh的函數。從圖1可以看出，f1(kh)和f2(kh)在有限水深區數值較大，而隨著水深的增大，兩者均趨于0。

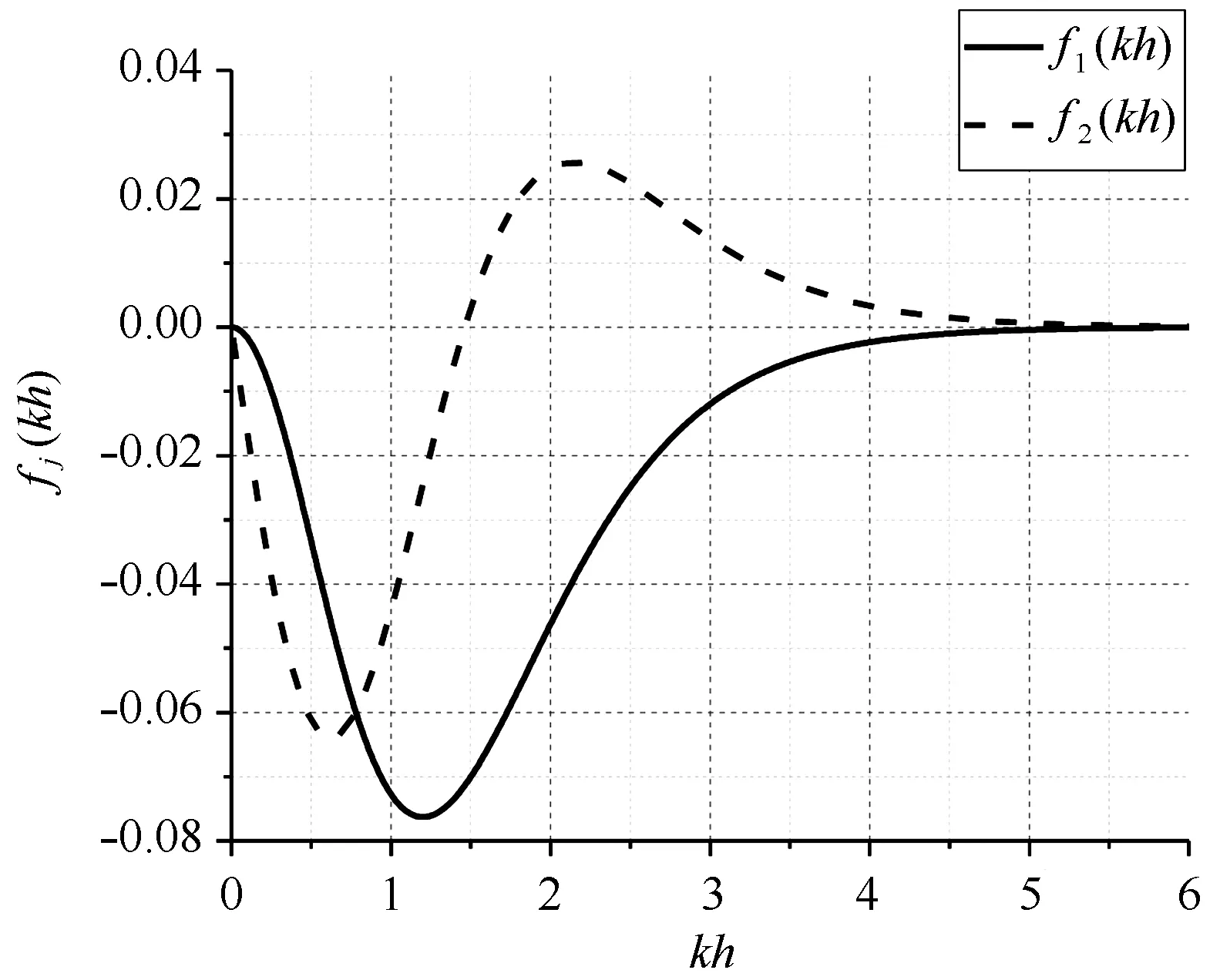
圖1 f1和f2隨相對水深kh的變化Fig.1 Variation of coefficients f1 and f2 with kh

當忽略地形曲率項和坡度平方項時，修正型緩坡方程就簡化為Berkhoff的緩坡方程：

▽·(ccg▽φ)+k2ccgφ=0.

(4)

當水深不變時，則轉換為Helmholtz方程：

▽2φ+k2φ=0.

(5)

3 有限元方程的建立

3.1 計算域的劃分

如圖2所示，將計算域劃分為內域和外域。其中，內域Ω1是地形變化區域，劃分六節點三角形單元網格，用單元插值函數作為權函數以建立有限元方程；外域Ω2是水深恒定區域，不劃分網格，用Hankel函數作為權函數，并應用格林公式將外域的面積分轉化為邊界Ba上的線積分以建立方程式；Ba為內外域的公共邊界，通常情況下取為圓周，通過Ba上的匹配條件可進行有限元方程的求解；Bb為物面邊界；B∞為無窮遠邊界。

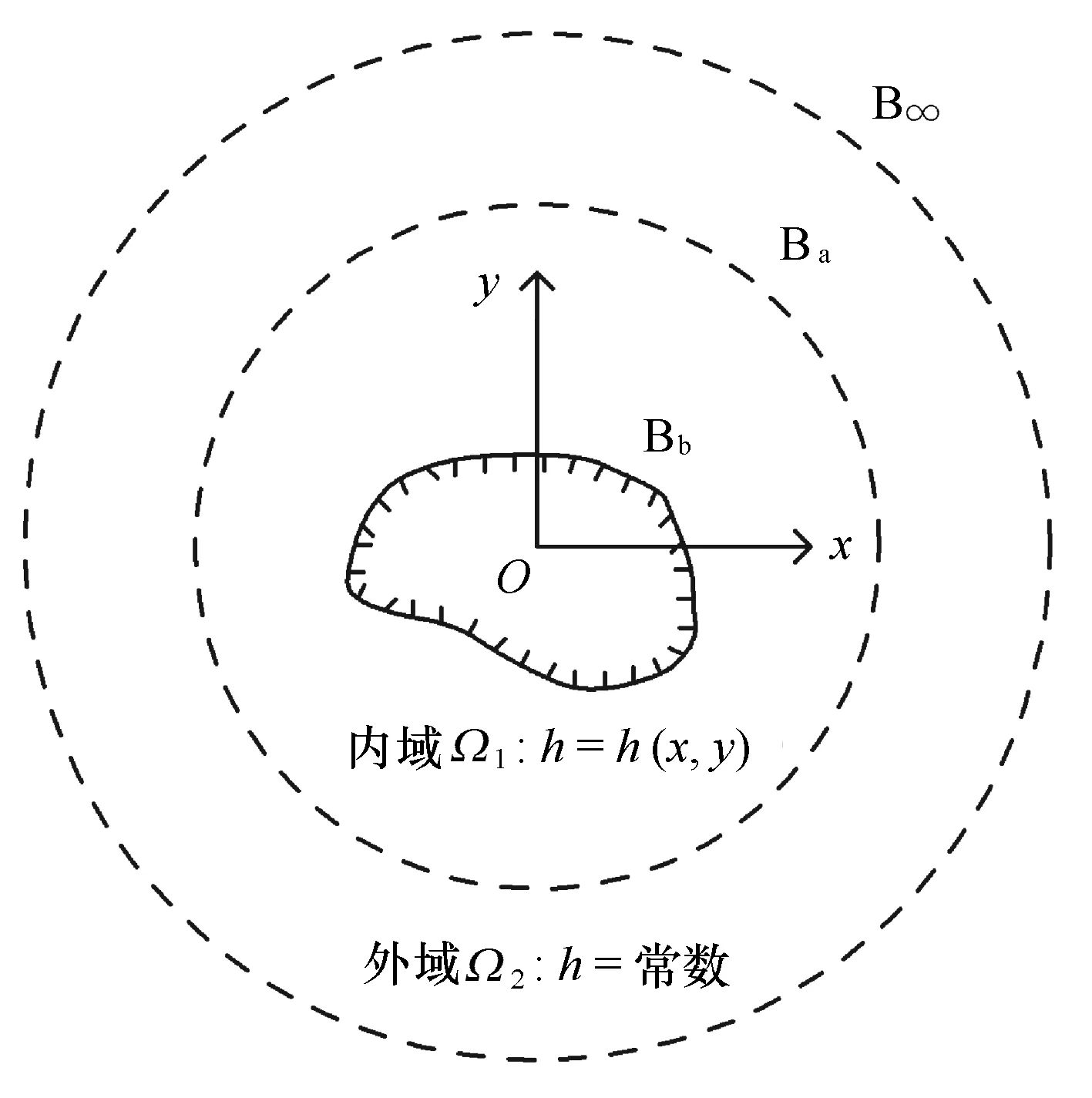
圖2 計算域劃分Fig.2 Division of computational domain

3.2 邊界條件

設內域Ω1的速度勢為φ，則在物面邊界Bb上滿足

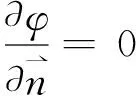
(6)

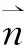
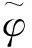
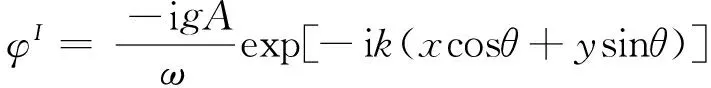
(7)

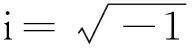
(8)

式中，r為Ω2域內x-y平面上某點到原點O的距離；φ為r與x軸正方向的夾角；Hn(kr)為n階第1類Hankel函數；An(n=0,1,2，…)和Bn(n=1,2，…)為待定系數。在n=N處截斷，并令G1=H0(kr)，G2i=Hi(kr)cosiφ，G2i+1=Hi(kr)siniφ，α1=A0，α2i=Ai，α2i+1=Bi(i=1,2,…，N)，式(8)可簡寫成：

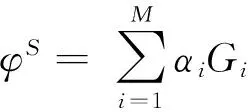
(9)

式中，M=2N+1。則無窮遠處輻射邊界條件可以表示為:

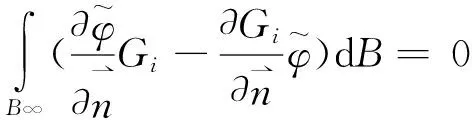
(10)

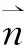
在公共邊界Ba上滿足：

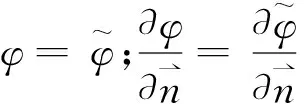
(11)

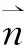
3.3 內域有限元方程

設φj為單元各節點速度勢，Nj為單元插值函數，則單元內的速度勢：

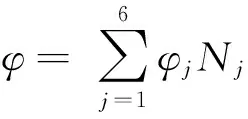
(12)

利用單元各節點的水深信息和單元插值函數，坡度平方項可表示為:

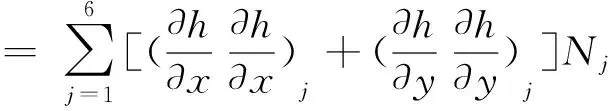
(13)

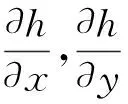
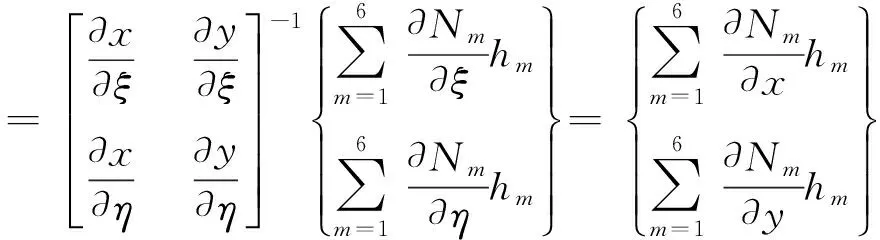
(14)

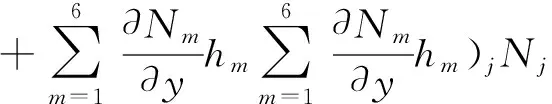
(15)

類似的，地形曲率項

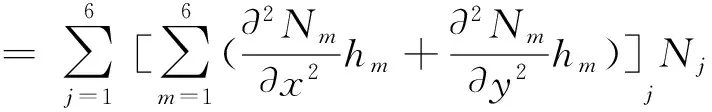
(16)

取單元插值函數Ni為權函數，利用Galerkin方法在單元內建立積分方程

[▽·(ccg▽φ)+(k2ccg+f1(kh)g▽2h

+f2(kh)gk(▽h)2)φ]NidΩ=0.

(17)

引入三節點線單元插值函數Li，對邊界Ba上的單元而言，Li為該單元外側邊界上的單元插值函數。將邊界Ba上的速度勢分解為入射勢φI和繞射勢φS，應用格林公式，式(17)可以重新寫成:

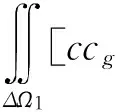
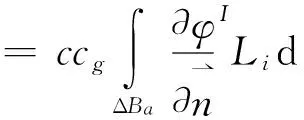
(18)

結合式(12)、(15)和(16)，可以寫成單元矩陣形式

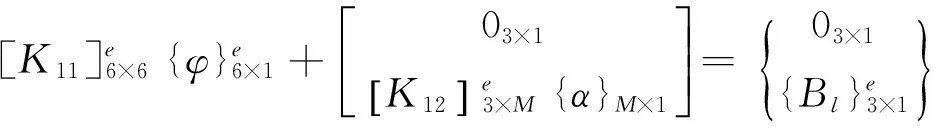
(19)

其中,

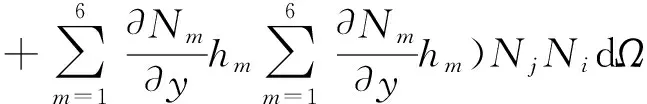
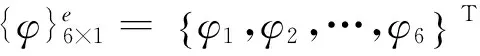
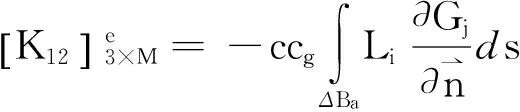
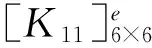
集合內域各單元矩陣可得:

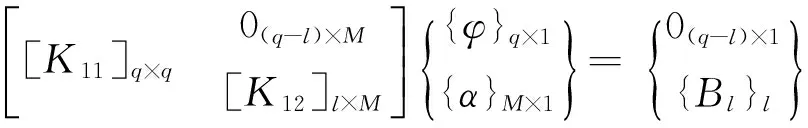
(20)

式中，q為總節點數；l為邊界Ba上的節點數。

3.4 外域方程式[12—13]

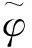
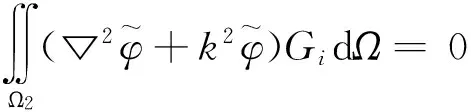
(21)

應用第二格林公式，式(21)可以寫成:

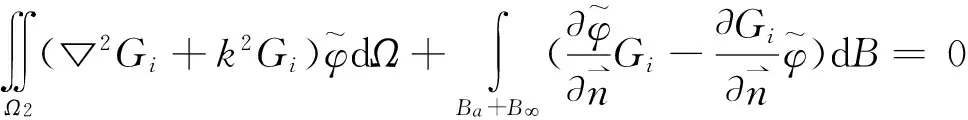
(22)

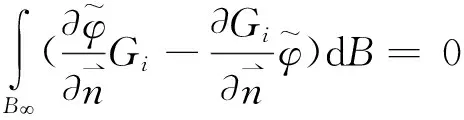
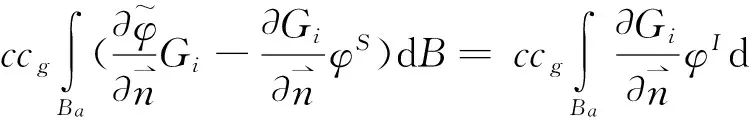
(23)

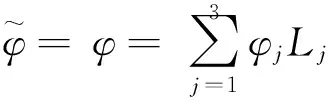
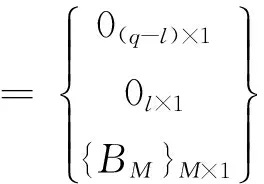
(24)

3.5 總矩陣方程

根據式(20)和式(24)，可以形成總矩陣方程

[K](q+M)×(q+M){φ}(q+M)×1={B}(q+M)×1.

(25)

式中，

；

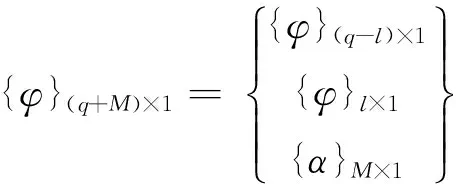
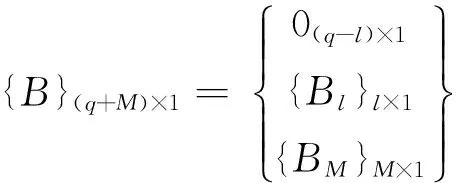
由于Ba為圓周，所以[K22]可用解析表達式表示

[K22]=2πkRccgdiag{H0′(kR)H0(kR),

H1′(kR)H1(kR),…,HM′(kR)HM(kR)},

(26)

式中,R為圓周Ba的半徑。

最后，本文采用列主元高斯消去法求解總矩陣方程式(25)。

4 結果驗證和討論

為了驗證本文修正型緩坡方程的有限元模型，首先計算了長波經過Homma島的繞射問題，計算結果與Zhai等[14]的解析解進行了比較；接著計算了圓形淺灘上波浪的繞射問題，計算結果與Suh等[6]的實驗數據進行了比較，并進一步探討了較陡地形對不同周期波浪的影響。

4.1 長波過Homma島的繞射問題

Homma島由旋轉拋物體及上部圓柱體組合而成。如圖3所示，上部圓柱體的半徑a=10 km，旋轉拋物體的底面半徑b=30 km。距島嶼中心r(單位：km)處的水深(單位：km)為:

(27)

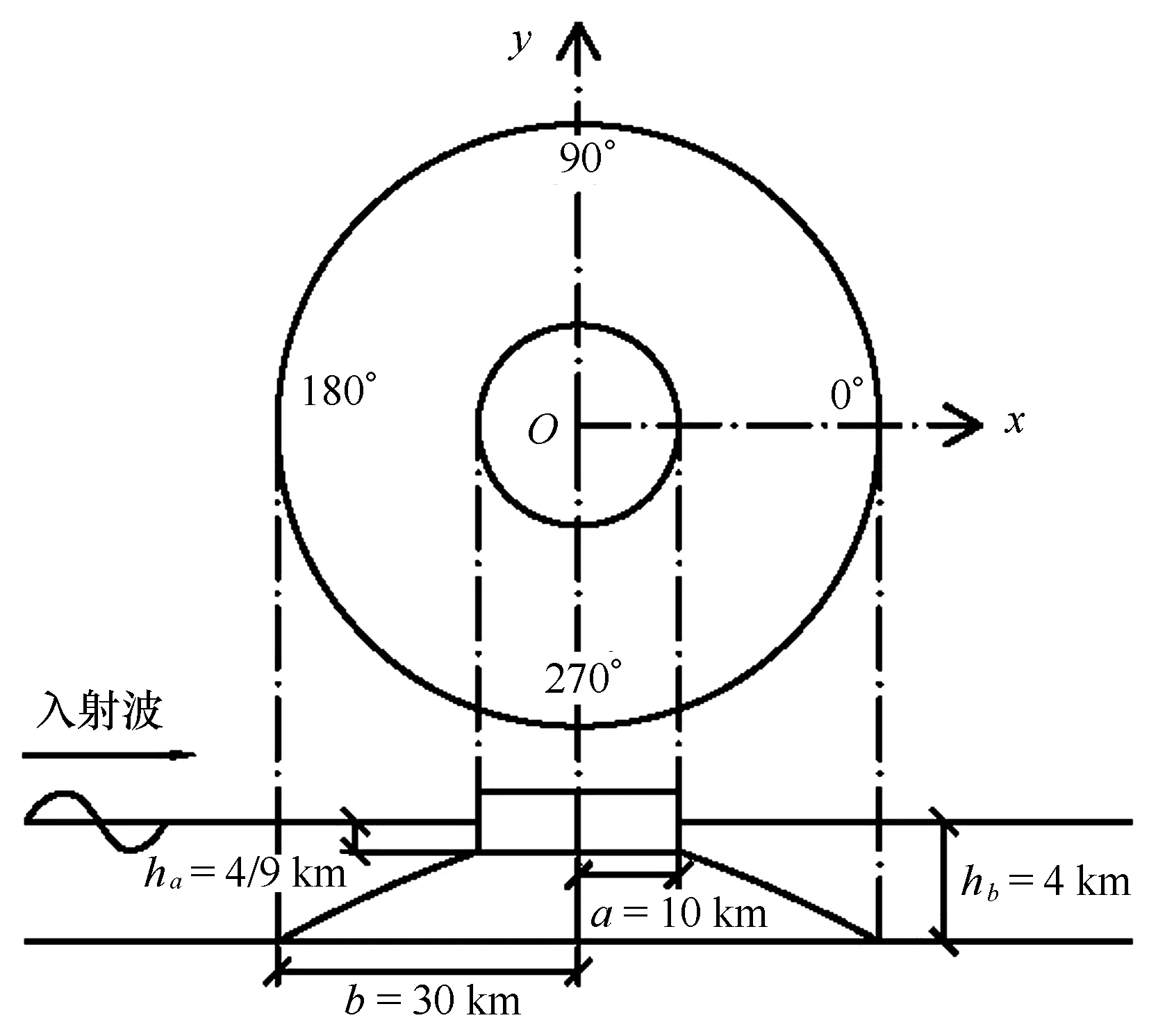
圖3 Homma島地形Fig.3 Sketch of Homma Island

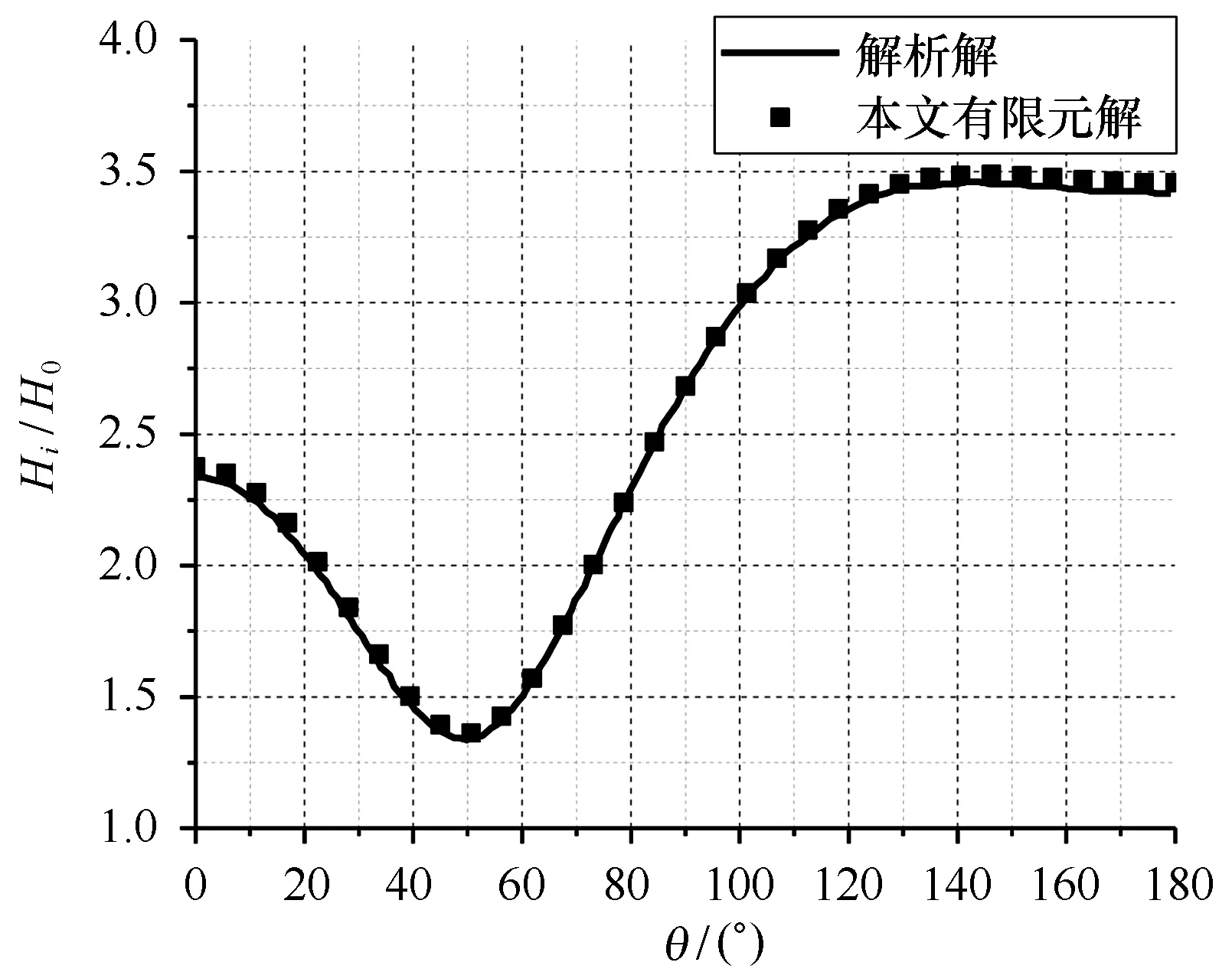
圖4 岸線圓周上修正型緩坡方程計算的相對波高和解析解的對比Fig.4 Comparison of calculated wave height by MMSE with analytical solutions along the shoreline

4.2 波浪過圓形淺灘的繞射問題

為了進一步驗證較陡地形上修正型緩坡方程有限元模型的正確性和應用范圍，本文將修正型緩坡方程有限元解、緩坡方程的有限元解與Sub等[6]的實驗結果進行比較。實驗設計的圓形淺灘地形如圖5所示，距淺灘中心r(0≤r≤R，單位：m)處的水深(單位：m)為:

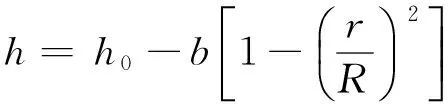
(28)

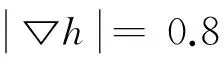
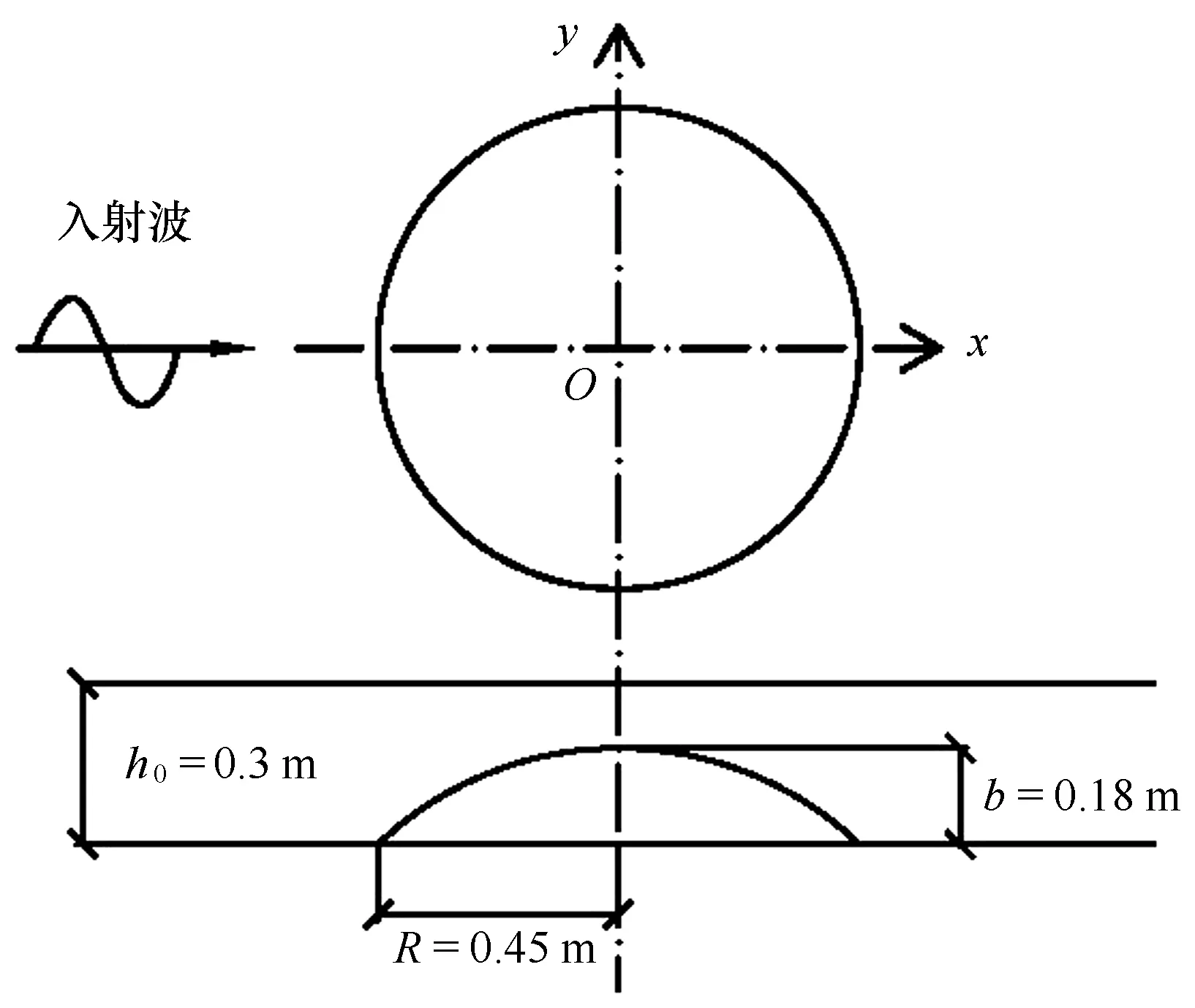
圖5 圓形淺灘地形Fig.5 Sketch of circular shoal

圖6是修正型緩坡方程和緩坡方程計算的y=0斷面上相對波高與實驗結果的對比。從圖中可以看出，相比緩坡方程，修正型緩坡方程的計算結果與實驗數據更加吻合，這說明在地形較陡的情況下，地形曲率項和坡度平方項對波浪的傳播變形會起到十分重要的作用。通過比較圖6a～c，并結合表1可以發現，在相對水深較大時，波高最大值發生在灘頂后方，而隨著相對水深的減小，波高的最大值有所增加，發生最大值的位置向前方移動，緩坡方程的計算結果在灘頂后方也表現出更大的誤差，這說明長波較短波更易受到地形曲率和坡度平方的影響。

5 結論

(1)本文建立了修正型緩坡方程的有限元模型，并應用該模型計算了波浪過Homma島和圓形淺灘的繞射問題，計算結果與翟西媛等的解析解和Sub等的實驗結果吻合良好，證明了本文有限元模型的正確性。

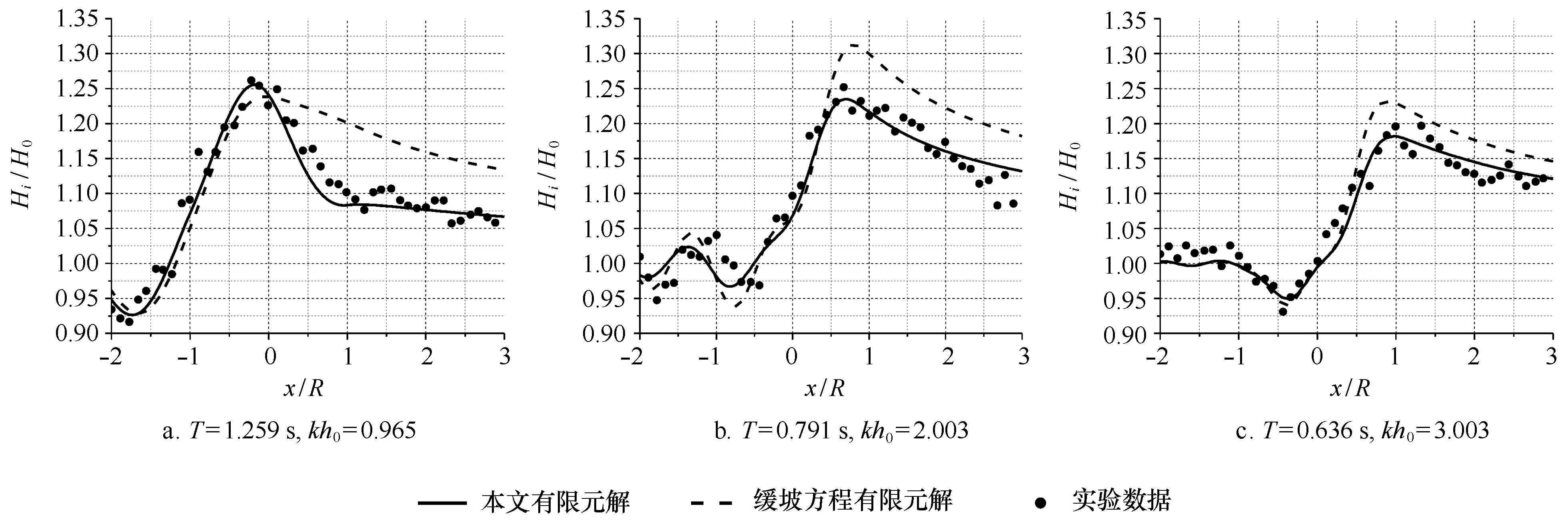
圖6 y=0斷面修正型緩坡方程和緩坡方程計算結果與實驗結果的對比Fig.6 Comparison of MMSE and MSE results with experimental data along y=0 section

波浪參數最大相對波高Hmax/H0最大相對波高發生位置x/R實驗結果MMSE計算結果MSE計算結果實驗結果MMSE計算結果MSE計算結果T=1.259s,kh0=0.9651.2621.2561.239-0.220-0.178-0.022T=0.791s,kh0=2.0031.2521.2351.3130.6670.7110.800T=0.636s,kh0=3.0031.1971.1821.2311.3251.0000.889

(2)通過本文修正型緩坡方程計算結果、緩坡方程計算結果和實驗數據的三者對比，可以看出，對于較陡地形上的波浪變形問題，修正型緩坡方程較緩坡方程具有更高的計算精度，這從側面證明了本文的有限元模型具有更寬的適用范圍。

(3)針對長波入射的情況，Homma島上部圓柱周圍的最大波高不是發生在迎浪點，而是對稱分布于迎浪點左右兩側，這與直立圓柱的情形不同。

(4)在地形坡度較陡的情況下，地形曲率項和坡度平方項會對波浪的傳播變形起到不可忽略的影響，并且隨著波浪周期的增大，波浪受地形曲率和坡度平方的影響也隨之增大。

[1] Berkhoff J C W. Computation of Combined Refraction-diffraction[M]. Delft Hydraulics Laboratory, 1974.

[2] Booij N. A note on the accuracy of the mild-slope equation[J]. Coastal Engineering, 1983, 7(3): 191-203.

[3] Kirby J T. A general wave equation for waves over rippled beds[J]. Journal of Fluid Mechanics, 1986, 162: 171-186.

[4] Chamberlain P G, Porter D. The modified mild-slope equation[J]. Journal of Fluid Mechanics, 1995, 291: 393-407.

[5] Chandrasekera C N, Cheung K F. Extended linear refraction-diffraction model[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1997, 123(5): 280-286.

[6] Suh K D, Lee C, Park Y H, et al. Experimental verification of horizontal two-dimensional modified mild-slope equation model[J]. Coastal Engineering, 2001, 44(1): 1-12.

[7] Silva R, Borthwick A G L, Taylor R E. Numerical implementation of the harmonic modified mild-slope equation[J]. Coastal engineering, 2005, 52(5): 391-407.

[8] 李孟國, 蔣德才. 關于波浪緩坡方程的研究[J]. 海洋通報, 1999, 18(4): 70-92.

Li Mengguo, Jiang Decai. A review on the study of mild-slope equation[J]. Marine Science Bulletin, 1999,18(4): 70-92.

[9] Chen H S, Mei C C. Oscillations and wave forces in a man-made harbor in the open sea[C]//Symposium on Naval Hydrodynamics, 10th, Proceedings, Pap and Discuss, Cambridge, Mass, June 24-28, 1974. 1976.

[10] Tsay T K, Liu P L F. A finite element model for wave refraction and diffraction[J]. Applied Ocean Research, 1983, 5(1): 30-37.

[11] Houston J R. Combined refraction and diffraction of short waves using the finite element method[J]. Applied Ocean Research, 1981, 3(4): 163-170.

[12] 趙明. 波浪作用下建筑物周圍的泥沙沖刷及海床演變[D]. 大連: 大連理工大學, 2002.

Zhao Ming. The local scour and topographical change around offshore structures under wave action[D]. Dalian: Dalian University of Technology, 2002.

[13] 趙明, 滕斌. 緩坡方程的有限元解[J]. 大連理工大學學報, 2000, 40(1): 117-119.

Zhao Ming, Teng Bin. Finite element solutions for mild slope equation[J]. Journal of Dalian University of Technology, 2000, 40(1): 117-119.

[14] Zhai X Y, Liu H W, Xie J J. Analytic study to wave scattering by a general Homma island using the explicit modified mild-slope equation[J]. Applied Ocean Research, 2013, 43: 175-183.

[15] Chau F P, Taylor R E. Second-order wave diffraction by a vertical cylinder[J]. Journal of Fluid Mechanics, 1992, 240(1): 571-599.

FEM model of the modified mild slope equation

Ni Yunlin1,2，Teng Bin1，Cong Longfei1

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China；2.SchoolofPortandTransportationEngineering,ZhejiangOceanUniversity,Zhoushan316022,China)

Compared with the mild slope equation, the bottom curvature and slope-squared terms are contained in the modified mild slope equation, which increases the complexity of solving the equation numerically. In this paper, the physical domain is divided into a finite inner region and an infinite outer region. The inner region of a variable depth is studied with the modified mild slope equation, and the outer region has a constant water depth, the velocity potential satisfying the Helmholtz equation. The bottom curvature and slope-squared terms in the equation are evaluated from the input bathymetry at each node of every element using the interpolation functions. With the boundary matching method and Gaussian elimination technique, the finite element equations are established and solved. Then, wave transformation over a Homma Island and a circular shoal is simulated respectively, and the results agree well with analytical solutions and experimental data, verifying the validity of the FEM model in this paper. Meanwhile, the comparison between the numerical and experimental results indicates the modified mild slope equation can provide more accurate predictions than the mild slope equation for wave propagation over relatively steep bathymetry.

the modified mild slope equation; finite element method; Homma Island; circular shoal

10.3969/j.issn.0253-4193.2017.01.011

2016-03-07；

2016-05-17。

國家自然科學基金(51379032，51490672)。

倪云林(1986—)，男，浙江省舟山市人，講師，博士生，主要從事波浪對海上建筑物作用的研究工作。E-mail:nylzjou@126.com

*通信作者：滕斌，教授，主要從事波浪對海上建筑物的作用研究。E-mail: bteng@dlut.edu.cn

P753

A

0253-4193(2017)01-0104-07

倪云林, 滕斌, 叢龍飛. 修正型緩坡方程的有限元模型[J]. 海洋學報, 2017, 39(1):104-110,

Ni Yunlin，Teng Bin，Cong Longfei. FEM model of the modified mild slope equation[J]. Haiyang Xuebao, 2017, 39(1): 104-110, doi: 10.3969/j.issn.0253-4193.2017.01.011