預期壽命與國民儲蓄率：基于可變增長率系數總儲蓄方程的分析

金 剛,張秋秋

(1.遼寧大學 人口研究所,遼寧 沈陽 110036; 2.沈陽大學 工商管理學院,遼寧 沈陽 110044)

?

預期壽命與國民儲蓄率：基于可變增長率系數總儲蓄方程的分析

金 剛1,張秋秋2

(1.遼寧大學 人口研究所,遼寧 沈陽 110036; 2.沈陽大學 工商管理學院,遼寧 沈陽 110044)

本文放松傳統生命周期假說關于個體壽命與工作期時長固定不變的假設，將一般形式的生存函數加入生命周期理論分析框架。與傳統生命周期假說總儲蓄方程中經濟增長率系數為常數的結論不同，研究發現加入生命函數的總儲蓄方程中經濟增長率的系數是可變的，15歲開始的預期壽命延長會顯著提高經濟增長率的系數，而15-60歲工作期預期壽命延長會顯著降低經濟增長率的系數，利用全球218個國家1981-2010年面板數據的實證結果較好地支持了前述結論。隨著預期壽命的延長，總儲蓄方程中經濟增長率系數有提高的趨勢，但包括中國、韓國在內的部分國家(地區)的經濟增長率系數提高幅度較大，這可能是這類國家(地區)國民儲蓄率的變動率明顯高于經濟增長率的變動率的原因。

預期壽命；工作期；經濟增長率；國民儲蓄率；可變增長率系數；總儲蓄方程

一、引 言

改革開放以來中國經濟保持著較快增速，伴隨著快速經濟增長，中國的國民儲蓄率水平也出現了明顯的提高，1980年中國國民儲蓄率為34.5%，2010年最高達到50.9%，2014年略微下降至48.8%①① 中國國家統計局網站。，按照世界銀行數據，2013年中國的儲蓄率水平在全球排名第五②② 世界銀行數據庫。。許多學者基于不同理論對中國高儲蓄現象進行了解釋，其中，生命周期理論是具有代表性的主流觀點之一。傳統生命周期理論的核心結論是在經濟和人口均衡時，總儲蓄率與經濟增長率具有近似的線性關系，因此快速的經濟增長可能是引致中國國民儲蓄率提高的主要原因。按照生命周期理論的基本結論，總儲蓄率的變化率與經濟增長率的變化率應該近似相等，美國和中國香港等國家和地區國民儲蓄率與經濟增長率的明顯同步特征基本印證了生命周期理論，但是，中國的現實情況卻與生命周期理論結論存在著一定的偏離，1981-2010年間，中國的國民儲蓄率的變化率明顯快于經濟增長率的變化率，也有其他的國家(地區)同樣顯示出了與中國類似的現象。圖1列出了1981-2010年中國、韓國、美國和中國香港的國民儲蓄率和GDP增長率的變動情況。

圖1顯示，1981-2010年美國和中國香港的國民儲蓄率與GDP增長率表現出較為明顯的同步特征，而相同時間段內，中國與韓國的情況卻有所不同。1981-2010年，中國經濟增長率相對穩定，而國民儲蓄率卻表現出明顯的上升趨勢，特別是在2001-2005年之后，中國GDP增長率小幅下降后略有上升，但國民儲蓄率卻表現為相對平穩之后的快速上升；韓國在1986-1990年之后經濟增長率呈現下降趨勢，而國民儲蓄率卻表現得比較平穩。分析其原因，我們認為有可能是中國以及韓國的經濟增長率對國民儲蓄率的邊際貢獻發生明顯的提高，從而引起國民儲蓄率增幅高于GDP增長率的增幅。

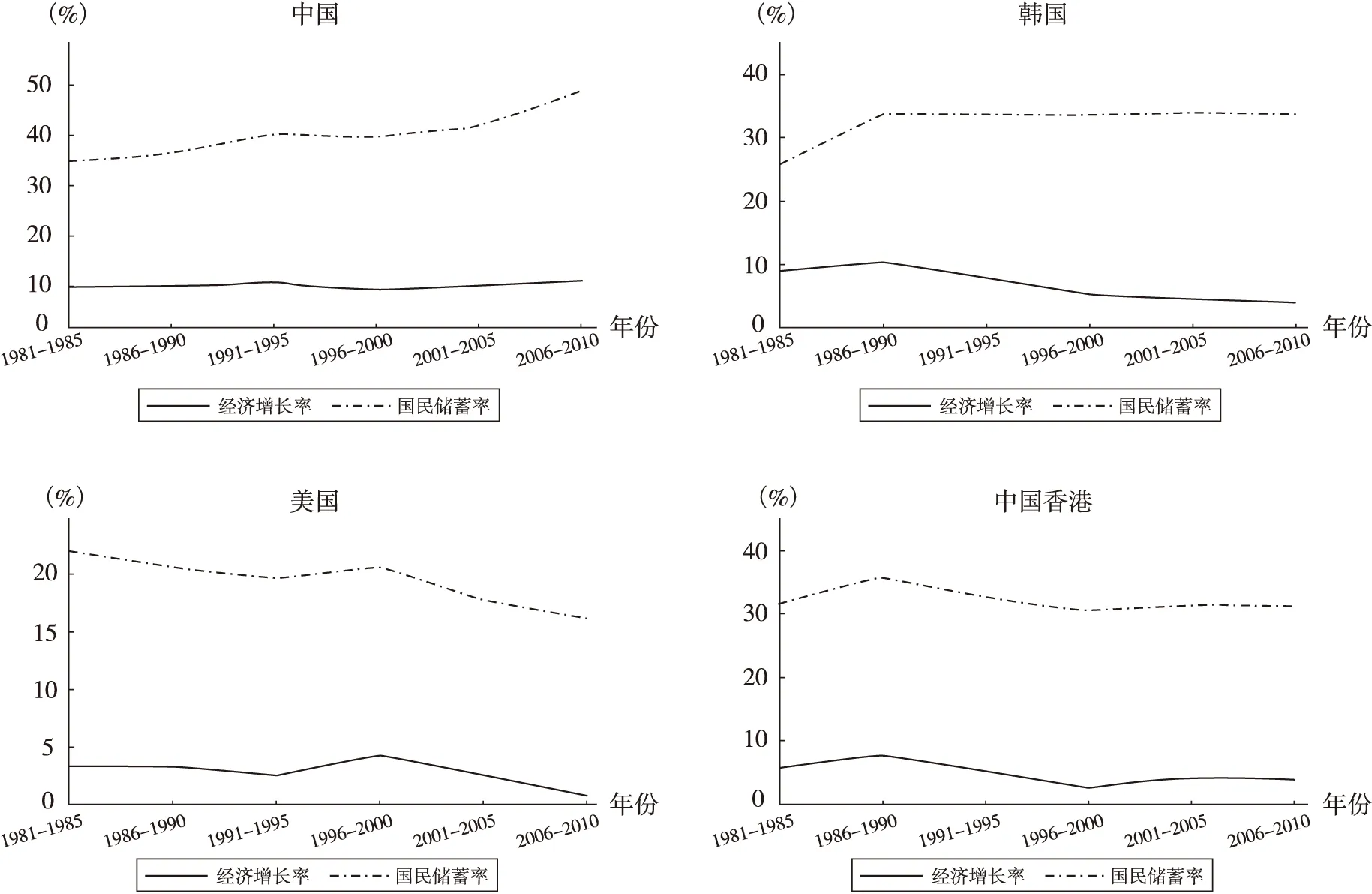
圖1 四國(地區)的經濟增長率與國民儲蓄率

按照傳統生命周期假說的觀點，總儲蓄率方程中經濟增長率的系數是由不同年齡個體未來壽命和未來工作期時長的函數所決定的，由于將生命時長和工作期時長均設定為常數，因此總儲蓄率方程中經濟增長率的系數為常數[1]。但是，現實條件下壽命和工作期時長都是數學期望值，會隨著生存概率的變化而發生變化，因此經濟增長率的系數也可能會隨之發生變化。預期壽命的變化本質上是生存概率變動的結果，傳統生命周期假說并未對生存概率以及預期壽命的影響進行分析，而目前針對預期壽命儲蓄效應的研究基本采取直接將預期壽命加入總儲蓄率方程的方法，從而可能忽略生存概率變動所引致的預期壽命變動對經濟增長率邊際儲蓄效應的影響。基于上述分析，本文嘗試將生存概率引入生命周期分析框架，在生存概率可變的條件下，通過個體消費加總來研究總儲蓄率的決定機制。研究發現預期壽命和工作期預期壽命與經濟增長率對國民儲蓄率具有交互影響，預期壽命與工作期預期壽命的變動會影響總儲蓄率方程中經濟增長率的系數，預期壽命的延長會提高經濟增長率的邊際儲蓄效應，工作期預期壽命的延長則會降低經濟增長率的邊際儲蓄效應。利用1981-2010年跨國面板數據的實證檢驗結果較好地支持了本文的理論分析結論。

本文共為五個部分，第二部分為文獻回顧，第三部分為加入生存概率后總儲蓄率決定的理論分析，第四部分利用1981-2010年跨國面板數據對理論分析結論進行實證檢驗，第五部分總結研究發現。

二、文獻回顧

Modigliani[1-2]等提出的生命周期假說，打破了凱恩斯絕對收入假說關于現期收入決定現期消費的研究視角，轉而重新回歸到消費者行為的基礎理論。該假說最具顛覆性的觀點是，消費者將建立實現一生效用最大化的消費儲蓄計劃安排，而某一時期的消費率僅是消費者一生計劃安排的一個方面。生命周期假說建立在消費者選擇理論基礎之上，并假設消費者效用由當期和未來各期消費共同決定，消費者各期可利用的資源是現期收入、未來收入折現值以及現期凈財富的總和，消費者將在此預算約束下通過各期消費的安排實現一生效用最大化，效用最大化的當期消費將是其可利用的資源、資本回報率以及年齡和未來壽命的函數。在個體消費決定基礎上，在預期壽命、利率、人口增長率等其它參數不變的假設下，通過對所有個體消費加總除以總收入所得到的總儲蓄率將是經濟增長率的函數，進一步對經濟增長率進行一階泰勒級數展開，生命周期假說得出的主要結論是，在人口與經濟均衡時，總儲蓄率與經濟增長率具有s≈α+β·g的線性關系，其中，s為總儲蓄率，g為經濟增長率。

傳統生命周期假說的核心假設之一是個體壽命與工作時長固定不變，由于壽命和工作時長是生命周期假說總儲蓄率方程中經濟增長率系數的決定因素，因此在該假設下經濟增長率的系數近似為常數。然而，現實中的預期壽命是不斷變化的，1950年以來全球預期壽命顯示出明顯的上升趨勢，1950-1955年全球出生時預期壽命僅為46.91歲，2010-2015年全球平均出生時預期壽命已經提高至70歲。預期壽命延長對儲蓄率的影響逐步引起了國內外學者的關注，Deaton[3-4]、Hurd[5]、劉生龍[6]等的研究發現出生時預期壽命的延長會顯著提高個體或家庭的儲蓄率，Lee[7-8]、范敘春[9]等研究發現出生時預期壽命延長會顯著提高總儲蓄率水平，金剛[10]等研究發現15-60歲工作期預期壽命的提高會顯著降低國民儲蓄率水平，60歲開始的老年期預期壽命的延長則會顯著提高國民儲蓄率水平。上述研究以實證方法為主，基本都采取了將預期壽命直接加入總儲蓄方程進行計量檢驗的方法，對于預期壽命變動影響個人儲蓄以及加總儲蓄的理論分析尚顯不足。Bloom[11]將生存概率引入生命周期理論分析框架，分析了預期壽命延長條件下的個體消費決策以及加總儲蓄決定，研究發現即使在自由選擇退休年齡條件下，預期壽命的延長依然具有顯著提高個體儲蓄率和總儲蓄率水平的效應。盡管該研究進一步推進了預期壽命儲蓄效應的理論分析，但也未關注預期壽命對總儲蓄率方程中經濟增長率系數的影響。同時，該研究將生存函數設定為指數分布的形式，由于指數形式的生存函數意味著個人在一生之中任何時間具有相同的死亡力，因此只適用于短期分析，而不適用于個人生命跨度長達幾十年的中長期分析。

相較于之前的研究，本文的改善主要體現在：(1)使用一般形式的生存函數替換目前研究中使用的指數分布生存函數，通過將一般形式生存函數加入生命周期理論研究框架，分析個體消費決策以及個體消費加總形成的總儲蓄決定機制；(2)引入分段預期壽命概念，分析15歲開始的預期壽命和15-60歲工作期預期壽命分別與經濟增長率的交互項對國民儲蓄率的影響效應，進而提出可變增長率系數總儲蓄率方程；(3)利用全球218個國家30年的面板數據，并通過每5年期取各變量平均值來克服短期經濟波動及測量誤差，對可變增長率系數總儲蓄方程進行實證檢驗。

三、理論分析

(一)個體消費

假設個體從出生開始生存至a歲的概率為sa(0)，ca為個體a歲時的消費，效用函數為對數形式U(ca)=ln(ca)，加入生存概率后，個體一生效用最大化問題可表示為：

(1)

其中，ρ≥0為時間偏好，ω為最高壽命。個體在任意時點面臨的預算約束為：

(2)

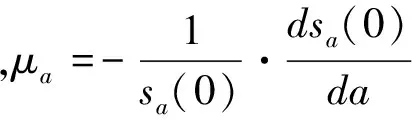
(3)

個體在任意年齡a歲的消費將為ca=co·e(r-ρ)a。假設個體無遺產動機，個體會實現一生消費精算現值與一生收入精算現值相等，初始消費占初始收入的比例將為：

(4)

其中，w0為個體在初始期的收入，σ為人均收入增長率，R為退休年齡。式(4)說明，為了實現一生的效用最大化，個體將在初始期選擇收入的一定比例進行消費，而這個比例獨立于當期收入。

(二)加總儲蓄率的決定

假設人口均衡增長率為n，經濟增長率將為g=σ+n。時刻T的總消費可以表示為各個年齡所有人消費的加總：

(5)

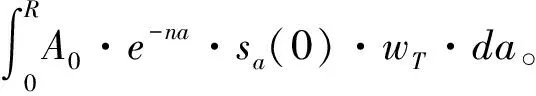
(6)

為了簡化分析，假設r=ρ=0，將初始消費比重式(4)代入式(6)，分別對eσa、e-ga和e-na在σ=g=n=0處進行一階泰勒級數展開，并左右兩邊取對數，利用ln(1+x)≈x，總儲蓄率方程可整理為：

+εT

(7)

(三)加入預期壽命的可變增長系數總儲蓄率

方程

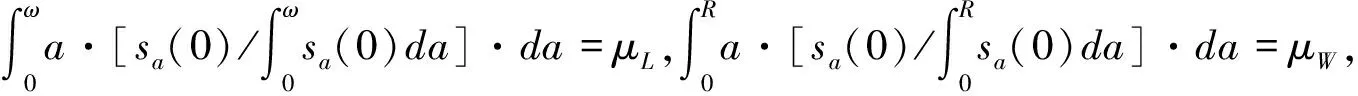
sT=α0+g·(μL-μW)+εT

(8)

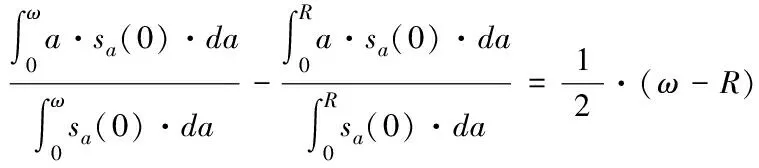
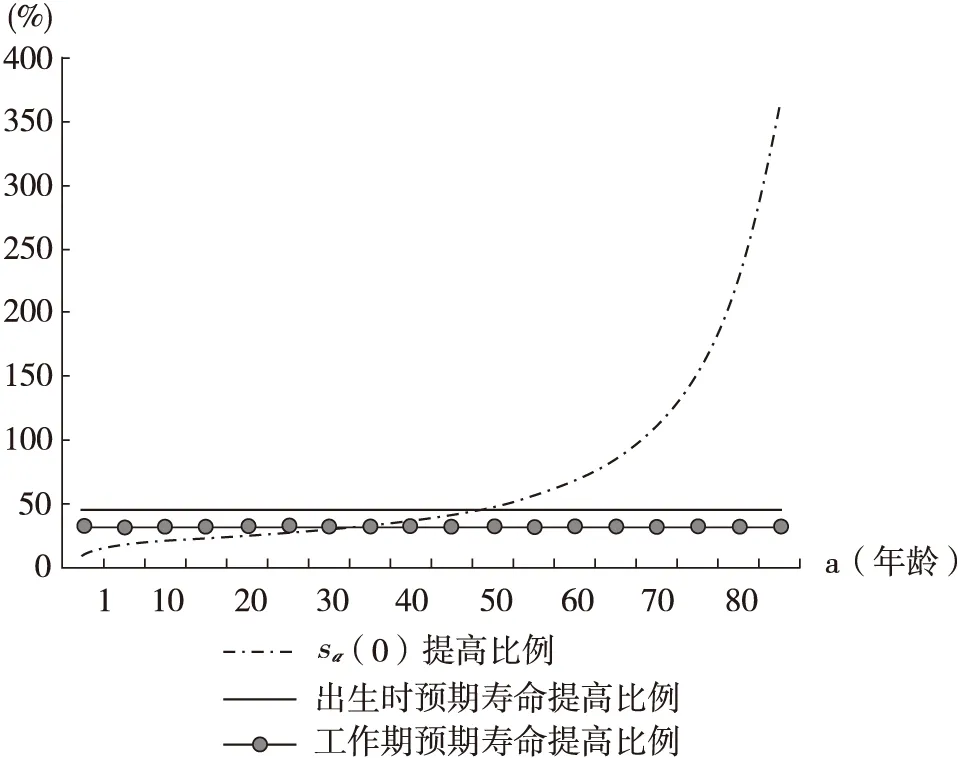
圖2 1950-2010年預期壽命與生存概率的提高比例

數據來源：聯合國人口司數據庫。

圖2顯示，從出生開始生存至a歲的概率sa(0)的提高比例明顯表現出遞增的趨勢，大約在45歲之前，sa(0)的提高比例小于出生時預期壽命的提高比例，而大約在45歲之后，sa(0)的提高比例高于出生時預期壽命的提高比例；工作期分段預期壽命提高比例與sa(0)提高比例的對比也顯示出基本一致的特征。

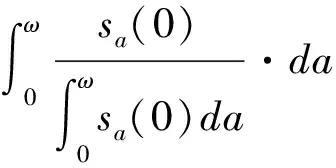
(9)

(10)

其中，z0-ω為出生時預期壽命，z0-R為工作期預期壽命。將式(9)、(10)帶入總儲蓄率方程式(8)，總儲蓄率方程可進一步表示為：

sT=α0+γ0·g+γ1·z0-ω·g-γ2·z0-R·g

(11)

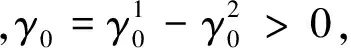
四、實證檢驗

(一)計量方程

由于個體不可能在出生時即開始工作，因此總儲蓄率方程式(11)中包含的預期壽命變量z0-R與z0-ω應該從工作期開始。然而，工作期的開始年齡和退休期的開始年齡在實證研究中獲得精確測定比較困難，原因是多方面的。首先，個體平均教育年限不斷增加，這意味著工作期開始年齡隨著預期壽命延長在不斷提高；其次，盡管目前世界上大多數國家都建立了養老保險制度并規定了退休年齡，但是退休年齡規定并不完全是強制性的，并且不同國家養老保險制度的退休激勵效應不同，因此提前退休和延遲退休在不同國家中都一定程度的存在；再次，部分國家的養老保險制度并不是全覆蓋的，部分人群可能依然處于養老保險制度覆蓋范圍之外。基于此，本文考慮利用勞動力年齡組劃分標準來構建z0-ω與z0-R的代理變量來對式(11)進行檢驗。對勞動力的年齡界定一般從15歲開始，因此我們假設15歲為工作期開始年齡，對老年人口的年齡界定有60和65歲兩種方法，我們將60歲設定為退休期開始年齡預期壽命與生存概率相關數據從聯合國人口司數據庫獲得，原始數據即為1980-1985，1985-1990，1990-1995，1995-2000，2000-200。在前述設定下有：

z0-ω=e15

(12)

z0-R=e15-45p15·e60

(13)

其中，e15為從15歲開始的預期壽命，e60為從60歲開始的預期壽命，45p15為15歲個體存活至60歲的概率。我們分析的是均衡狀態下總儲蓄率的決定，由于指標短期波動會對總儲蓄率產生影響，因此我們采用Kraay[12]的方法對各個指標每五年取平均值以降低指標短期波動程度，這種處理方法也有利于降低各指標的測量誤差。同時，由于消費習慣等原因，人們面對約束條件的變化時，消費水平不可能立刻轉變，總儲蓄率的變動也不可能即刻完成，這意味著不同均衡狀態之間的轉換需要一定的時間。因此，我們參照Bloom[11]等的方法，將儲蓄率的滯后項加入計量方程。根據已有的研究結果，人口撫養比以及出生時預期壽命可能對總儲蓄率水平具有影響，因此我們在儲蓄率方程中進一步加入了人口結構變量和出生時預期壽命。計量方程確定為：

sT=α0+β0·g+β1·z0-ω·g+β2·z0-R·g+β3·sT-1+∑βi·Xi+εT

(14)

其中，g為經濟增長率，z0-ω為15歲開始的預期壽命，z0-R為15至60歲的工作期分段預期壽命，sT-1為滯后一期的儲蓄率，Xi為少兒人口比重(youthratio)、老年人口比重(oldratio)和出生時預期壽命(e0)。根據理論分析結果，我們預期β0>0，β1>0，β2<0。

(二)數據處理及描述性統計

我們搜集了包括中國在內的全球218個國家的儲蓄率、經濟增長率、預期壽命等指標從1981至2010年共30年的數據，并對所搜集的數據按照每五年一個時間段計算平均值。本文使用的儲蓄率為國內總儲蓄占國內生產總值的比重，經濟增長率為按照相同價格測算的年增長率。少兒人口比重為0-14歲人口比例，老年人口比重為65歲及以上人口比重。對各變量每五年取平均值之后①① 預期壽命與生存概率相關數據從聯合國人口司數據庫獲得，原始數據即為1980-1985，1985-1990，1990-1995，1995-2000，2000-2005，2005-2010各時間段的取值；其他變量我們從1981年開始每5年取平均值，即為1981-1985，1986-1990，1991-1995，1996-2000，2001-2005，2006-2010年的平均值。，所有變量描述性統計情況見表1。

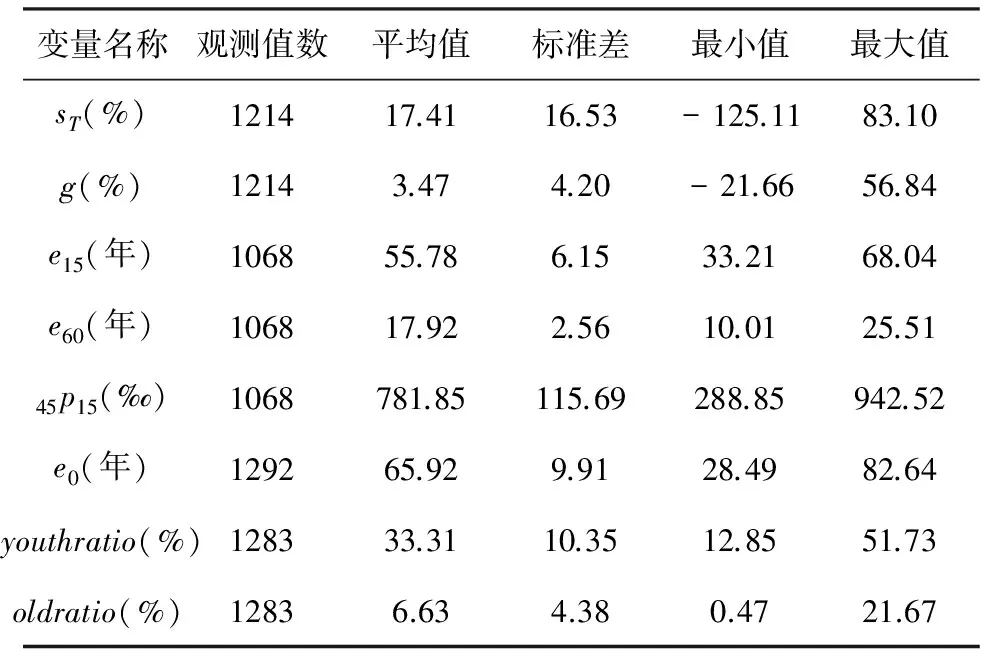
表1 變量的描述性統計

注：預期壽命與生存概率數據來自聯合國人口司數據庫，其他數據來自世界銀行數據庫。

(三)估計結果

我們首先使用固定效應方法對理論分析結論進行檢驗，估計結果見表2。模型(1)的自變量僅包含經濟增長率，經濟增長率的系數顯著為正，與生命周期假說的基本結論一致。在模型(1)的基礎上，模型(2)加入了本文主要關注的經濟增長率與預期壽命相關變量的兩個交互項，估計結果顯示，z0-ω·g的系數顯著為正，z0-R·g的系數顯著為負，與理論分析結論一致。模型(3)進一步加入了滯后一期的儲蓄率。模型(4)增加了人口結構變量，模型(5)增加了出生時預期壽命，估計結果也與之前模型的估計結果基本一致。從固定效應方法估計結果來看，經濟增長率的系數顯著為正，經濟增長率與15歲開始的預期壽命的交互項z0-ω·g的系數顯著為正，經濟增長率與15-60歲工作期分段預期壽命的交互項z0-R·g的系數顯著為負，這一結果較好地支持了本文的理論分析結論。

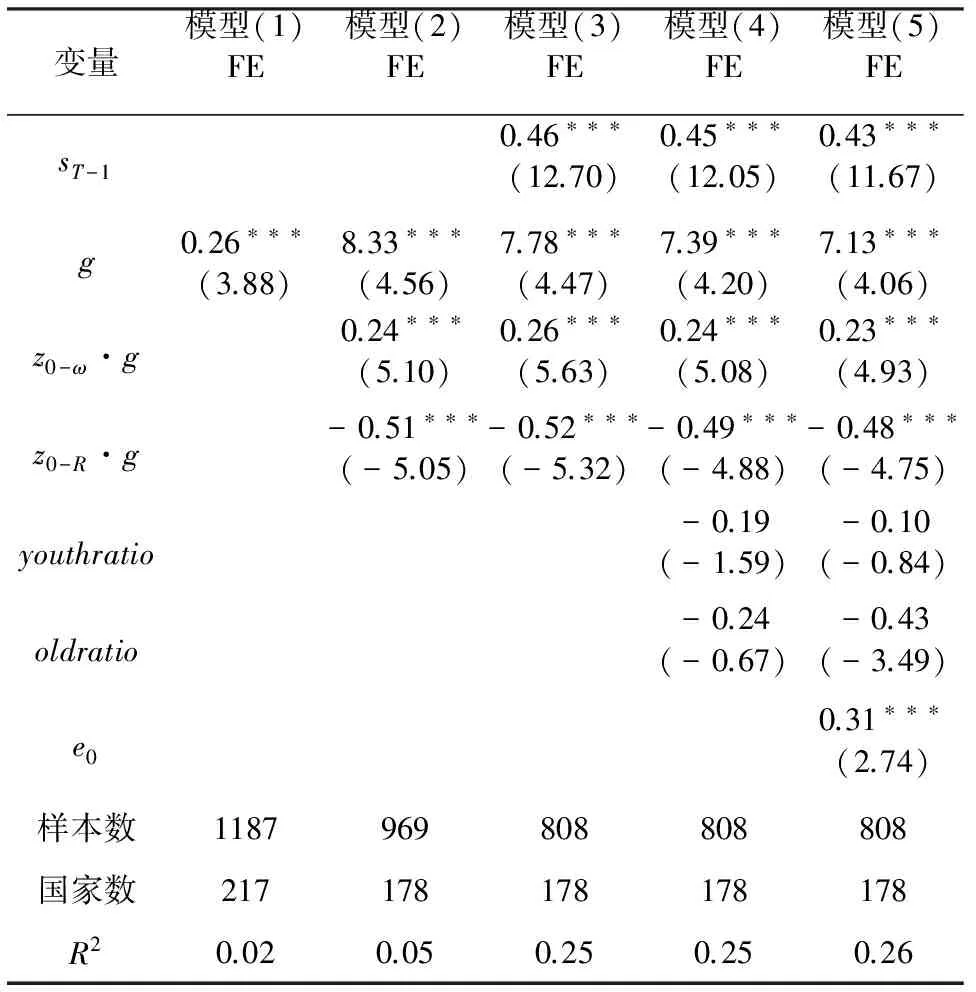
表2 固定效應方法估計結果

注：利用stata 14.0進行估計；省略常數項結果；*、**、***分別表示在10%、5%、1%水平上顯著；括號內為t值。下同。

動態面板數據條件下，滯后因變量與誤差項相關，同時，總儲蓄率方程中的誤差項可能與經濟增長率相關。為了解決內生性造成的估計結果偏誤，本文進一步利用動態面板估計方法對總儲蓄率方程進行檢驗。同時，為了提高模型的穩健性，我們根據世界銀行對不同國家(地區)按照收入水平的分組方法，將總體樣本分為高收入組和低收入組進行分組動態面板估計。動態面板方法的估計結果見表3。

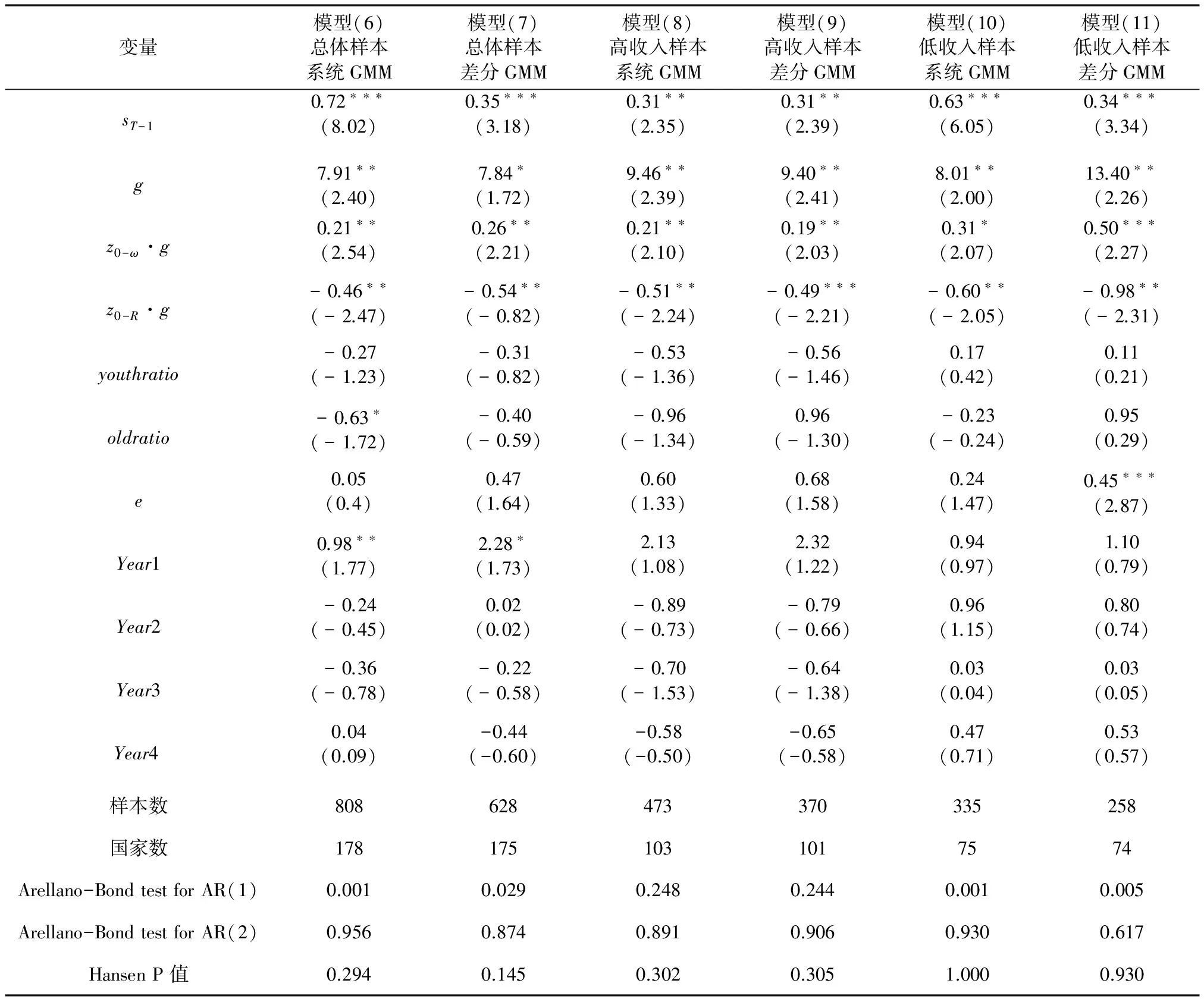
表3 動態面板方法估計結果

注：時間虛擬變量作為外生變量，將滯后一期的儲蓄率以及模型中的其他自變量作為內生變量，滯后期設定為5期。

模型(6)為總體樣本的系統GMM估計，模型(7)為總體樣本的差分GMM估計，從估計結果來看，滯后一期儲蓄率的系數顯著為正，經濟增長率與預期壽命交互項的系數顯著為正，經濟增長率與15歲開始的工作期預期壽命交互項的系數顯著為負，估計結果與固定效應估計結果基本一致。模型(8)與模型(9)分別為高收入組樣本的系統GMM估計和差分GMM估計，估計結果與總體樣本基本一致。模型(10)與模型(11)為低收入組樣本的系統GMM估計和差分GMM估計，估計結果也與其他模型一致。總體樣本與分組樣本動態面板估計結果也較好地支持本文的理論研究結論。值得注意的是，在加入生存概率之后，少兒人口比重、老年人口比重和出生時預期壽命的系數在動態面板估計中顯著性都不高，人口因素對總儲蓄率的影響主要體現在預期壽命和工作期預期壽命分別與經濟增長率對國民儲蓄率的交互影響，這也意味著較前研究中直接將出生時預期壽命加入計量方程進行檢驗的方法可能是值得商榷的。

根據本文的研究結果，生命周期假說的總儲蓄率方程應該表示為式(11)，隨著預期壽命的變動，經濟增長率的系數將是可變的。按照Modigliani[1]的研究結論，在出生時預期壽命和工作期時長不變的情況下，總儲蓄率方程中經濟增長率的系數將是主要由出生時預期壽命和工作期時間長度的函數所決定的常數。但是，加入生存概率后，由于預期壽命和工作期預期壽命都是可變的，因此經濟增長率的系數也將是可變的。本文的理論研究結論和實證估計結果都證明了預期壽命對經濟增長率的國民儲蓄邊際效應大小具有影響。具體來看，15歲開始的預期壽命的延長會顯著提高經濟增長率的系數，而15-60歲工作期預期壽命的延長則會顯著降低經濟增長率的系數。

根據金剛[10]等的研究，全球平均15歲開始的預期壽命仍在普遍延長，而工作期預期壽命在部分國家特別是相對高收入國家(地區)已經呈現出穩定的趨勢。同時，圖2也顯示出，出生時預期壽命的增長比例明顯高于工作期預期壽命的增長比例。在這種預期壽命以及工作期預期壽命的變動趨勢下，我們推測經濟增長率的系數是逐步增大的。利用總體樣本的系統GMM估計結果計算，中國1981-1985年經濟增長率的系數約為0.24，2006-2010年經濟增長率系數提高至0.69，經濟增長率以及經濟增長率系數的變動共使國民儲蓄率增長了約5.44個百分點，占同期中國國民儲蓄率增長的32.62%。表4列出了根據估計結果計算的1981-2010年美國、中國香港、中國和韓國的經濟增長率對國民儲蓄率邊際影響效應的變動情況。

表4 1981-2010年根據實證分析結果計算的四國(地區)系數變動情況

注：根據模型(6)相關變量系數計算。

表4中數據顯示，四國(地區)總儲蓄方程中經濟增長率系數都是逐步增大的，但是美國和中國香港經濟增長率系數的增長明顯要更平穩，相鄰時間段經濟增長率系數提高的幅度約為10%～20%，并且增幅有下降的趨勢。中國與韓國的情況與美國和中國香港不同，中國經濟增長率系數在2001-2005年之前小幅增長，但在2001-2005年增長幅度接近100%，從圖1來看，這個時點與中國國民儲蓄率增速從2005年開始明顯快于GDP增速大致相吻合；韓國在1986-1990年經濟增長率系數比前一時間段提高了一倍以上，相鄰時間段經濟增長率系數的增幅一直保持在接近50%的水平，明顯高于美國和中國香港的增速。在實證檢驗中本文將退休年齡設定為60歲，考慮到預期壽命延長條件下勞動力實際退出勞動力市場的年齡可能會有一定程度的延后，這會引起工作期預期壽命的提高并進而一定程度上抵消經濟增長系數的提高，因此美國和中國香港這類經濟增長率系數變動幅度較低的國家和地區的實際經濟增長率系數可能會比較穩定，從而使國民儲蓄率與經濟增長率表現為同步的變化，而中國與韓國這類經濟增長率系數出現大幅度提高的國家，即使在去除其他因素的影響后，經濟增長率系數可能也是明顯提高的，因此表現為國民儲蓄率的變動率高于GDP增長率的變動率，這可以在一定程度上解釋圖1顯示出的國民儲蓄率與GDP增長率變動的兩類不同特征。

在一定的醫療、經濟和社會發展等條件下，預期壽命不可能無限上升，工作期預期壽命也將趨于穩定，因此經濟增長率系數提高的趨勢不會一直延續，隨著預期壽命的穩定，經濟增長率的系數也會趨于平穩，這將與傳統生命周期理論的基本結論相符。例如，表4中數據顯示中國香港2001-2005年和2006-2010年的經濟增長率系數增幅已經下降至10%以下，其原因是中國香港的預期壽命在全球排名第二，相對于預期壽命較低的國家和地區，中國香港預期壽命的增長速度開始相對放緩。從這個意義上說，傳統生命周期理論將預期壽命與工作時長設定為常數的方法，適用于人類壽命達到極限之后的穩定狀態，而在此之前，預期壽命主要呈現增長趨勢，預期壽命的變動使經濟增長對國民儲蓄率的邊際影響效應發生著變化。

五、研究結論與政策涵義

本文的主要研究結論是：(1)在生命周期理論分析框架中加入生存概率之后，預期壽命的變化會引起總儲蓄率方程中經濟增長率的系數發生變化，即經濟增長率的系數是可變的。(2)15歲開始的預期壽命與15-60工作期預期壽命分別與經濟增長率對國民儲蓄率具有交互影響，15歲開始預期壽命的延長會增大總儲蓄率方程中經濟增長率的系數，而工作期預期壽命的延長則會使總儲蓄率方程中經濟增長率的系數減小。在經濟增長率不變時，15歲開始預期壽命的延長將使國民儲蓄率提高，而工作期預期壽命的延長將國民儲蓄率水平降低。(3)隨著預期壽命的延長，總儲蓄率方程中經濟增長率的系數有提高的趨勢，部分國家和地區的經濟增長率系數提高幅度較大，這可以在一定程度上解釋中國、韓國等國家的國民儲蓄率的變動率明顯高于經濟增長率的變動率的現象。按照本文的測算結果，1981-2010年間，經濟增長率以及經濟增長率系數的提高，使中國國民儲蓄率增長了約5.44個百分點，占同期中國國民儲蓄率增長的32.63%。

近期中國經濟增長有小幅放緩的趨勢，這在一定程度上會降低國民儲蓄率水平，但由于預期壽命的延長，中國的經濟增長率對國民儲蓄率的邊際影響效應可能將會進一步提高，經濟增速放緩降低國民儲蓄率的效果將會減小，如果以降低國民儲蓄率和提高消費水平作為政策目標，在預期壽命延長的條件下，實施延遲退休制度以提高個人對工作期時長的預期，強化管理以有效解決提前退休問題，建立養老金計發激勵機制以促進個體延長工作和繳費年限，完善勞動力市場為老年人口提供適當的就業機會和崗位等辦法，可以成為有效的政策選擇。

[1] Ando A, Modigliani F. The “life-cycle”hypothesis of saving: Aggregate implications and tests[J].American Economic Review, 1963, 53(1): 55-84.

[2] Modigliani F, BrumbergR. Utility analysis and the consumption function: An interpretation of cross-section data[A]. Kurihara K K. Post-Keynesian Economics[M].Rutgers University Press, 1954.388-436.

[3] Deaton A, Paxson C. Saving, growth, and aging in Taiwan[A].Studies in the Economics of Aging[C]. University of Chicago Press, 1994.331-362.

[4] Deaton A, Paxson C. Growth, demographic structure, and national saving in Taiwan[J]. Population and Development Review, 2000, 26(Supplement): 141-173.

[5] Hurd M D, McFadden D L,Gan Li. Subjective survival curves and life cycle behavior[A]. Inquiries in the Economics of Aging[M]. University of Chicago Press, 1998. 259-309.

[6] 劉生龍, 胡鞍鋼, 郎曉娟. 預期壽命與中國家庭儲蓄[J]. 經濟研究, 2012(8):108-118.

[7] Lee R, Mason A, Miller T. Saving, wealth and the demographic transition in East Asia[R]. East-West Center Working Paper, Population Series No. 88-7,1997.

[8] Lee R, Mason A, Miller T. Life cycle saving and the demographic transition: the case of Taiwan[J]. Population and Development Review, 2000, 26(Supplement): 194-219.

[9] 范敘春,朱保華.預期壽命增長、年齡結構改變與我國國民儲蓄率[J].人口研究, 2012(4):20-30.

[10] 金剛,柳清瑞, 張秋秋.分段預期壽命對國民儲蓄率的影響效應[J]. 中國人口科學,2015(3):69-78.

[11] Bloom D E, Canning D, Mansfield R, Moore M. Demographic change, social security systems, and savings[J]. NBER Working Paper No.12621, 2006.

[12] Karry A. Household saving in China[J].The World Bank Economic Review, 2000, 14(3): 545-570.

責任編輯、校對：鄭雅妮

2016-04-26

本文得到國家哲學社會科學基金青年項目“人口老齡化高峰期養老保險基金缺口應對研究”(12CRK010)和遼寧省教育廳優秀人才支持計劃(WJQ2014003)的資助。

金剛(1976- )，遼寧省撫順市人，經濟學博士，遼寧大學人口研究所副研究員，研究方向：人口與社會保障；張秋秋(1978- )，女，遼寧省沈陽市人，經濟學博士，沈陽大學工商管理學院副教授，研究方向：人力資源與社會保障。

A

1002-2848-2016(06)-0064-09