基于矩陣分析的苧麻織物生物拋光工藝參數優化

舒服華

武漢理工大學 職業技術學院(中國)

基于矩陣分析的苧麻織物生物拋光工藝參數優化

舒服華

武漢理工大學 職業技術學院(中國)

提出了一種正交試驗與矩陣分析相結合的苧麻織物生物拋光整理工藝參數多目標優化方法。以正交試驗的數據為基礎，利用矩陣分析法優化苧麻織物生物拋光整理工藝參數。該優化方法可克服單一正交試驗優化方法數據處理過于簡單、優化結果精度不高的缺點，提高決策的準確性。

苧麻； 正交試驗； 矩陣分析； 模糊一致矩陣； 權重； 優化

隨著人們生活水平的提高，對服飾的要求不斷提高，服裝材料也隨之呈現出多樣化發展。當前，“崇尚自然、返樸歸真”成為一種社會時尚，這使得一些傳統的服裝材料重新受到消費者的青睞。苧麻纖維的吸濕透氣性好，苧麻纖維制成的織物穿著涼爽、強度高、硬挺度好，并具有天然抗菌等優良特性，深受消費者的喜愛。但苧麻織物較硬，穿著容易產生刺癢感，這在一定程度上影響了其服用性及其產品的開發。對苧麻織物進行生物拋光整理，可使其表面光潔、抗起毛起球性好，同時具有柔軟、蓬松等獨特的性能[1][2]24。生物拋光整理是采用生物酶去除織物表面絨毛的一種整理方法。若工藝參數選取得當，可獲得滿意的整理效果，反之，不僅不能獲得拋光效果，還會破環織物原有的性能。

正交試驗是一種高效、快速的試驗方法，但這種方法對數據的處理較為簡單，當因素和水平及目標較多時，難以做出準確的判斷。矩陣分析法在多因素、多目標問題的優化方面具有獨特的優勢。為此，本文將正交試驗法與矩陣分析法相結合，對苧麻織物生物拋光整理工藝參數進行優化，以彌補單一正交試驗優化方法的不足。

1 試驗設計及試驗結果

1.1 材料與儀器

試驗材料：JP-1型纖維素酶，醋酸，醋酸鈉，純苧麻坯布。

試驗儀器：FA 2004型電子天平，HHS型電熱恒溫水浴鍋，DZF-6050型真空干燥箱，PHSJ-4A型實驗室pH計，YG 026型斷裂強度測試儀，YG 811型懸垂性測試儀。

1.2 試驗方法

在纖維素酶用量(染料相對織物質量的百分數，o.w.f)為1%～3%、浴液溫度為45～60 ℃、pH值為4.5～6.0(pH值采用醋酸-醋酸鈉緩沖溶液調節)、浴比為1∶15的條件下對苧麻織物進行生物拋光處理30～60 min，然后用80 ℃水沖洗10 min，使酶失活后，烘干。

1.3 測試指標與方法

1.3.1 減量率

將纖維素酶生物拋光處理前后的苧麻織物試樣置入烘箱中，采用105 ℃溫度烘干至質量恒定，按式(1)計算減量率。

(1)

式中：E——減量率；

G1——生物拋光處理前苧麻織物的質量；

G2——生物拋光處理后苧麻織物的質量；

A——苧麻織物的含水率。

1.3.2 斷裂強力

纖維素酶生物拋光處理前后苧麻織物試樣的斷裂強力按GB/T 3923—1997測定，生物拋光處理后試樣的強降率按式(2)計算。

(2)

式中：K——試樣的強降率；

P1——生物拋光處理前試樣的斷裂強力；

P2——生物拋光處理后試樣的斷裂強力。

1.3.3 毛效

測量含0.5%(質量分數)重鉻酸鉀的蒸餾水在30 min內沿織物試樣垂直方向的上升高度。

1.3.4 懸垂性能

采用懸垂性測試儀上測定生物拋光處理前后苧麻織物試樣的懸垂系數，織物懸垂系數的計算式如式(3)。

(3)

式中：F——試樣的懸垂系數；

m1——與試樣相同大小的紙張的質量；

m2——與試樣投影圖相同大小的紙張的質量；

m3——與夾持盤相同大小的紙張的質量。

1.4 工藝參數與工藝目標的優化

影響苧麻織物生物拋光工藝效果的工藝參數主要有酶用量、浴液溫度、浴液pH值、整理時間及浴比，根據相關研究，浴比為1∶15時苧麻織物的生物拋光效果較為理想[2]26，因此本文將浴比設定為1∶15，以其他4個工藝參數作為優化對象進行優化。評價苧麻織物生物拋光的質量指標主要有減量率、強降率、懸垂系數及毛效，為便于定量分析，選取減量率、強降率、懸垂系數和毛效作為綜合優化目標。采用L16(44)正交試驗表，進行4因素4水平正交試驗設計，正交試驗的因素水平如表1所示，試驗結果如表2所示。

表1 苧麻織物拋光因素水平表

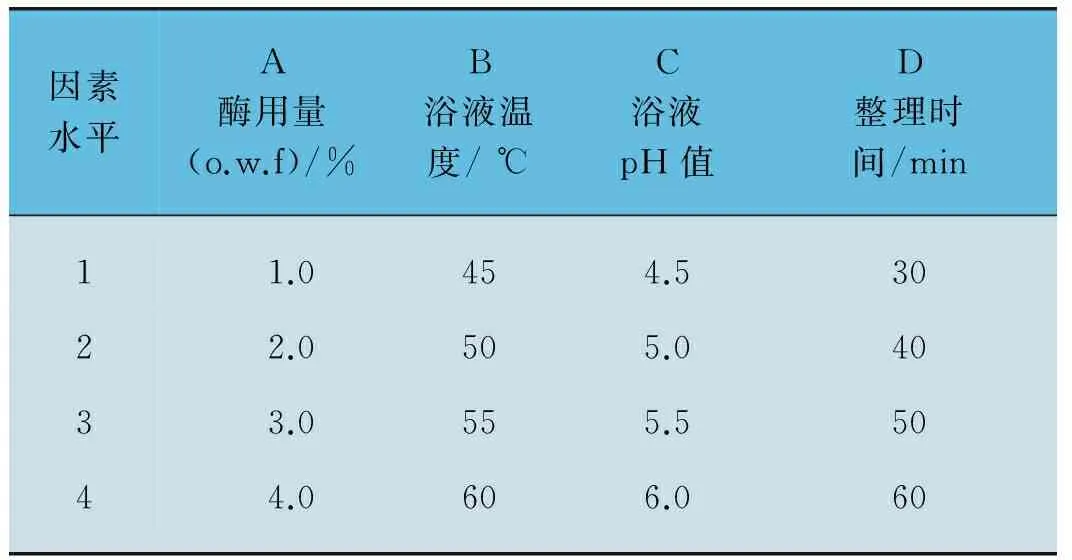
因素水平A酶用量(o.w.f)/%B浴液溫度/℃C浴液pH值D整理時間/min1 1.0454.5302 2.0505.0403 3.0555.5504 4.0606.060

2 矩陣分析法

2.1 數據分析

根據表2的試驗結果，可求得各工藝參數不同工藝水平下對應的工藝目標的平均值和級差，以及在單工藝目標下的推薦最優參數組合，結果如表3所示。其中，Ki為各因子在i(i=1，2，3，4)水平時各測試指標的平均值；R為極差，表示同一因子的Ki中最大值與最小值之差。R越大，該因素對試驗結果的影響越顯著。

表2 苧麻織物拋光試驗結果

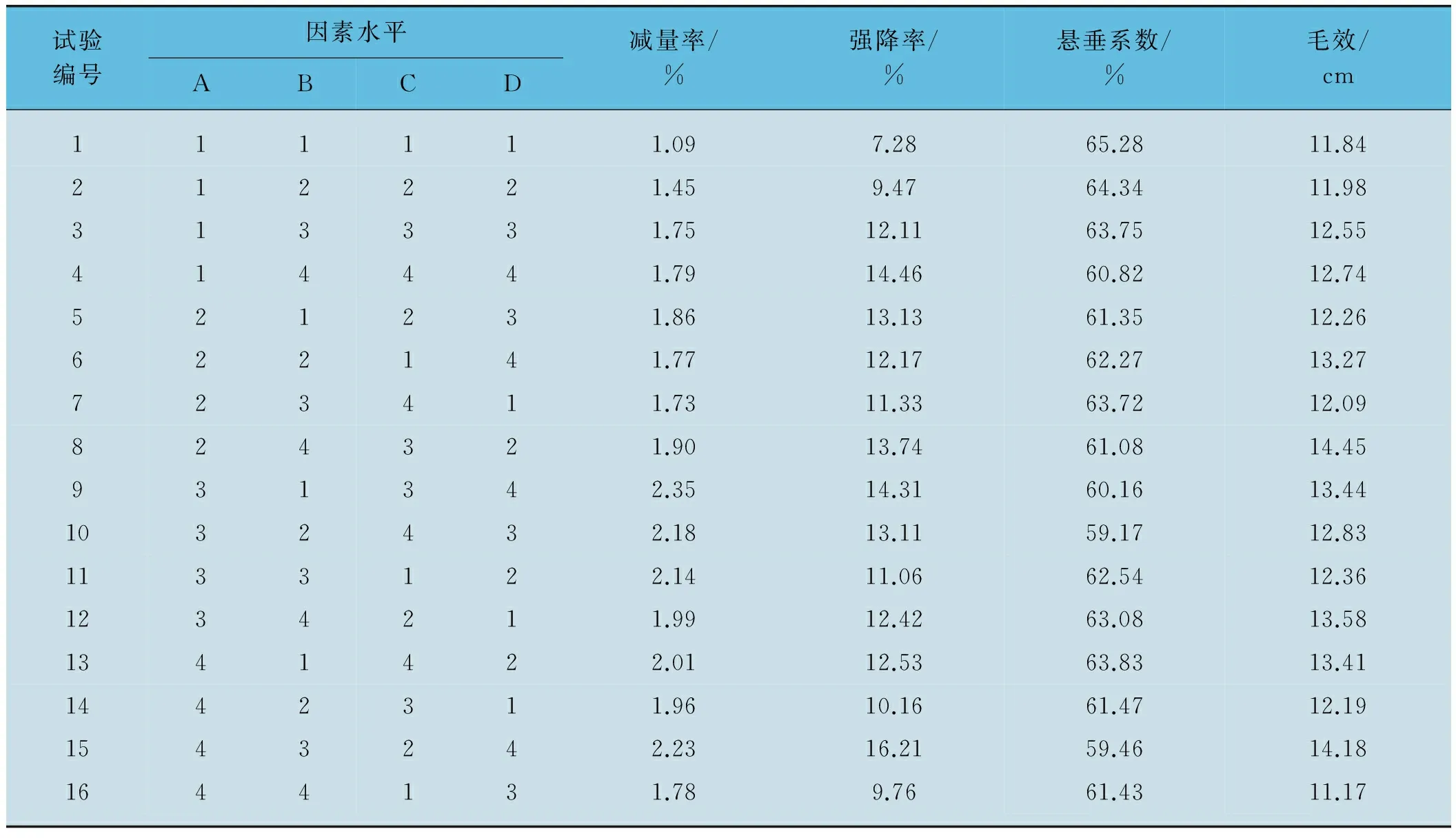
試驗編號因素水平ABCD減量率/%強降率/%懸垂系數/%毛效/cm111111.097.2865.2811.84212221.459.4764.3411.98313331.7512.1163.7512.55414441.7914.4660.8212.74521231.8613.1361.3512.26622141.7712.1762.2713.27723411.7311.3363.7212.09824321.9013.7461.0814.45931342.3514.3160.1613.441032432.1813.1159.1712.831133122.1411.0662.5412.361234211.9912.4263.0813.581341422.0112.5363.8313.411442311.9610.1661.4712.191543242.2316.2159.4614.181644131.789.7661.4311.17

表3 不同工藝參數水平下對應工藝目標的平均值

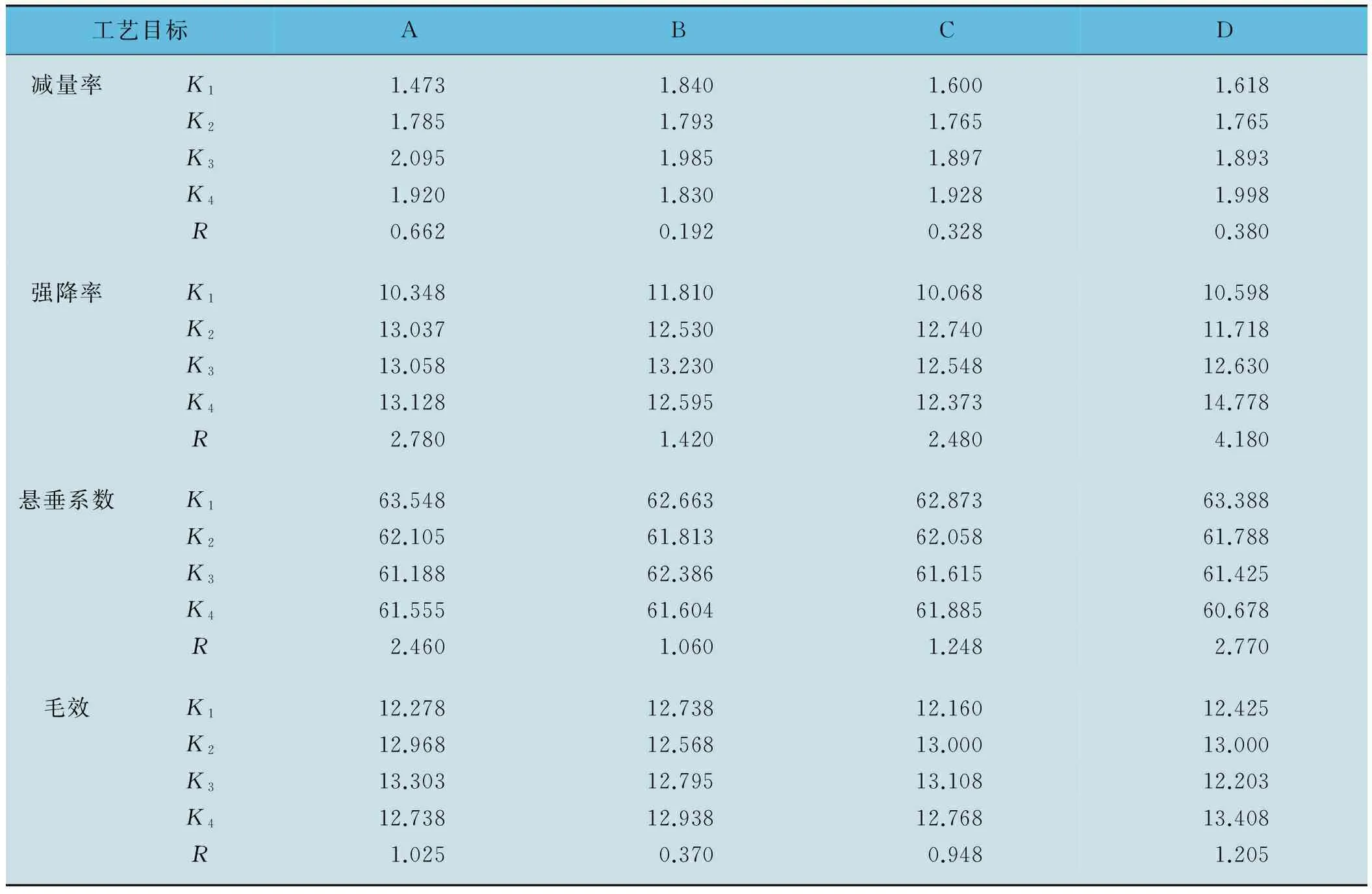
工藝目標ABCD減量率K11.4731.8401.6001.618K21.7851.7931.7651.765K32.0951.9851.8971.893K41.9201.8301.9281.998R0.6620.1920.3280.380強降率K110.34811.81010.06810.598K213.03712.53012.74011.718K313.05813.23012.54812.630K413.12812.59512.37314.778R2.7801.4202.4804.180懸垂系數K163.54862.66362.87363.388K262.10561.81362.05861.788K361.18862.38661.61561.425K461.55561.60461.88560.678R2.4601.0601.2482.770毛效K112.27812.73812.16012.425K212.96812.56813.00013.000K313.30312.79513.10812.203K412.73812.93812.76813.408R1.0250.3700.9481.205

由表3可知，就減量率而言，各因素的影響程度由大到小依次為酶用量、整理時間、浴液pH值和浴液溫度，推薦組合為A3B3C3D4；就強降率而言，各因素的影響程度由大到小依次為整理時間、酶用量、浴液pH值和浴液溫度，推薦組合為A1B1C1D1；就懸垂系數而言，各因素的影響程度由大到小依次為整理時間、酶用量、浴液pH值和浴液溫度，推薦組合為A3B4C3D4；就毛效而言，各因素的影響程度由大到小依次為整理時間、酶用量、浴液pH值和浴液溫度，推薦組合為A3B4C3D1。

2.2 多工藝目標優化

2.2.1 評價矩陣構建

評價矩陣由各因素取不同水平時所獲得的工藝目標值的算術平均值構成。對于工藝目標k(k=1，2，3，4)，若其取值越大越優，則評價矩陣如式(4)所示；若其取值越小越優，則評價矩陣如式(5)所示。

Mk=(ai1，ai2，ai3，ai4)

(4)

Mk=(1/ai1，1/ai2，1/ai3，1/ai4)

(5)

式中，ai1，ai2，ai3，ai4(i=1，2，3，4)分別表示因素A，B，C，D取水平i時對應的目標k的算術平均值。

2.2.2 矩陣規范化

由于評價矩陣中的元素具有不同的量綱和數量等級，為便于比較，需對評價矩陣進行規范化，見式(6)。

(6)

式中，akj為第i個因素取4種水平時對應工藝目標k值的算術平均值。

2.2.3 優勢矩陣構建

優勢矩陣是將同一因素在不同水平上的重要程度與不同因素對同一工藝目標影響程度進行融合的一種判別矩陣，是衡量工藝水平優劣的重要指標。對于工藝目標k，優勢矩陣如式(7)所示。

(7)

(8)

式中，λi為優度系數；Ri(i=1，2，3，4)為在工藝目標k下因素i的極差。

2.2.4 權重確定

在多工藝目標優化問題中，很難實現同時使每個工藝目標都處于最優狀態，但也不能平均對待每個工藝目標，應根據不同要求及實際情況，對其中一個或幾個有所側重和突出，通常是通過賦予其一定的權重加以體現的。本文通過模糊一致矩陣確定工藝目標的權重，其優點是計算簡單且無需進行一致性檢驗。

模糊一致矩陣確定工藝目標權重的基本方法[3-4]：首先對工藝目標的重要性進行兩兩比較，然后根據表4所示的標度法法則確定評分，構造優先關系矩陣(互補矩陣)D。

D=(dij)

(9)

式中，dij為工藝目標i相對于工藝目標j的得分，其中，dii=0.5；dji=1-dij。

表4 標度值確定

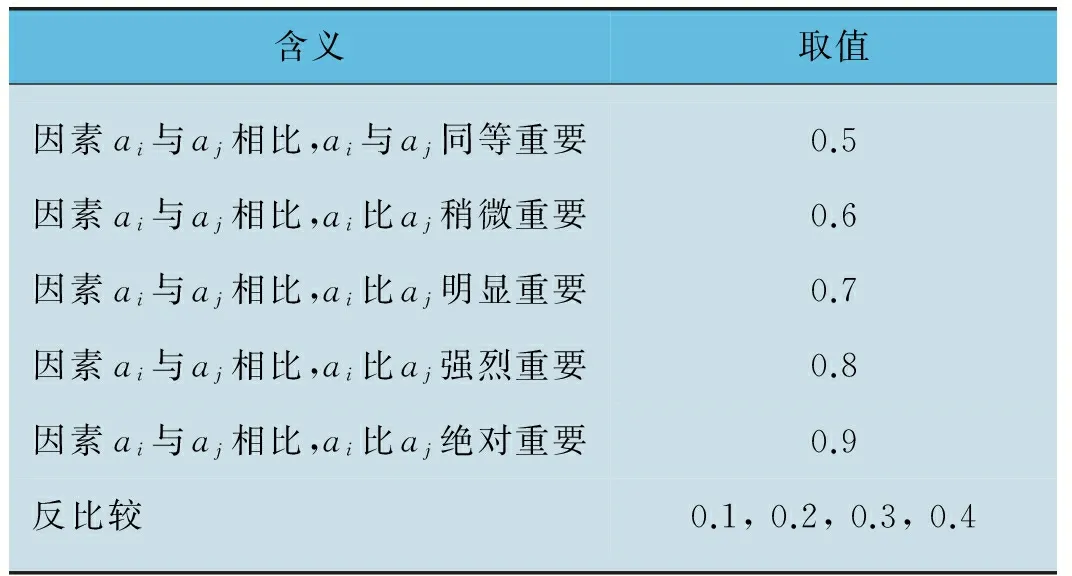
含義取值因素ai與aj相比,ai與aj同等重要0.5因素ai與aj相比,ai比aj稍微重要0.6因素ai與aj相比,ai比aj明顯重要0.7因素ai與aj相比,ai比aj強烈重要0.8因素ai與aj相比,ai比aj絕對重要0.9反比較0.1,0.2,0.3,0.4

根據優先關系矩陣構造模糊一致矩陣E：

E=(eij)

(10)

(11)

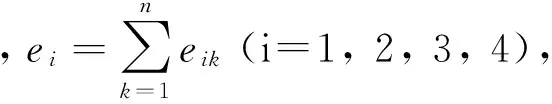
根據模糊一致矩陣，求各工藝目標的權重，如式(12)所示。

(12)

式中，α為由用戶定義的系數，需滿足α≥(n-1)/2。

2.2.5 決策矩陣確定

決策矩陣是整個多目標優化問題的評判矩陣，根據決策矩陣可確定優化工藝參數組合。決策矩陣如式(13)所示。

(13)

3 計算實例

以苧麻織物生物拋光的其中一個工藝目標——減量率計算為例，構建決策矩陣。在苧麻織物的拋光工藝中，通常在一定范圍內減量率越大越好，為此，可根據式(4)構建評價矩陣如下

各因素的極差R1=0.122，R2=0.192，R3=0.328，R4=0.380，極差之和為1.522。則由式(8)可得優度系數λ1=0.408 8，λ2=0.126 1，λ3=0.215 5，λ4=0.249 6，結合式(7)，可得針對減量率的優勢矩陣為

同理，可求得苧麻織物生物拋光處理后的強降率、懸垂系數及毛效的優勢矩陣分別為

根據表4，可構造優勢關系矩陣為

取α=4，結合式(10)和式(11)可求得模糊一致矩陣為

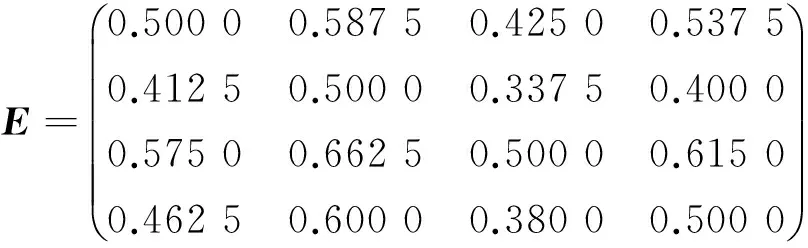
按式(12)可求得工藝目標的權重集W=(0.256，0.207，0.294，0.243)，即失量率權重w1=0.256，強降率權重w2=0.207，懸垂系數權重w3=0.294，毛效權重w4=0.243。

將權重值代入式(13)可得決策矩陣：

其中，決策矩陣的列對應工藝因素A、 B、 C、 D，行對應工藝水平1、 2、 3、 4。由決策矩陣可知，苧麻織物生物拋光處理的工藝參數優化組合為A4B3C3D4，即優化工藝參數為酶用量4%、浴液溫度55 ℃、浴液pH值5.5、整理時間60 min。

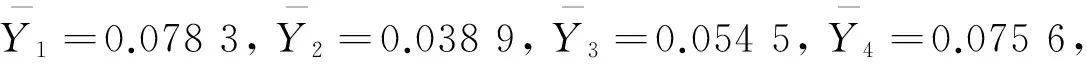
4 結語

矩陣分析法在優化工藝條件時，不僅考察因素水平對目標值的差異，還考慮因素水平目標值的極差影響，并且在多目標優化問題中引入權重區分工藝目標之間的差異，既可實現在同一因素之間進行縱向比較，又可實現在不同因素之間進行橫向比較，篩選更全面，結果更準確可靠。本文基于正交試驗法，采用矩陣分析法對苧麻織物生物拋光工藝參數進行多工藝目標優化，并用模糊一致性矩陣確定各工藝目標的權重，避免了一致性檢驗的麻煩。該方法計算簡便，分辨率高，可取得滿意的結果。

[1] 文飛，陳德兆.苧麻織物的生物拋光工藝優化[J].印染助劑，2006，23(6)：14-15.

[2] 朱俊萍.崔淑玲.APL酶對苧麻織物拋光處理最佳工藝的研究[J].印染助劑，2008，25(11).

[3] 伍毅.阮競蘭.矩陣分析法在膠輥礱谷機工作參數優化中的應用[J].河南工業大學學報(自然科學版)，2012，33(5)：83-88.

[4] 張吉軍.模糊一致判斷矩陣3種排序方法的比較研究[J].系統工程與電子技術，2003，25(11)：1370-1372.

Optimization on bio-polishing process parameters of ramie fabric based on the matrix analysis

ShuFuhua

SchoolofCareerTechnical，WuhanUniversityofTechnology，Wuhan/China

A multi objective optimization method combined with orthogonal experiment and matrix analysis was presented for the bio-polishing process parameters of ramie fabric. Based on the data of orthogonal experiment，the bio-polishing process parameters of ramie fabric were optimized by matrix analysis. The optimization method could overcome the shortcomings that the data processing was too simple and the precision of the optimization result was not high，and could effectively improve the accuracy of decision making.

ramie； orthogonal experiment； matrix analysis； fuzzy consistent matrix； weight； optimization