感悟方法探索規律
王鵠
人教版《數學》五年級下冊《探索圖形》是在認識長方體和正方體后,安排的一節綜合與實踐活動。目的是讓學生運用學過的正方體的特征等知識,探索由小正方體拼成的大正方體表面涂色再分開后,每個小正方體表面涂色的可能性及每種可能的數量和位置特征,培養學生的空間想象能力和推理能力,體會分類計數、數形結合、歸納、推理、模型等數學思想。
一、化繁為簡,明確探究方向
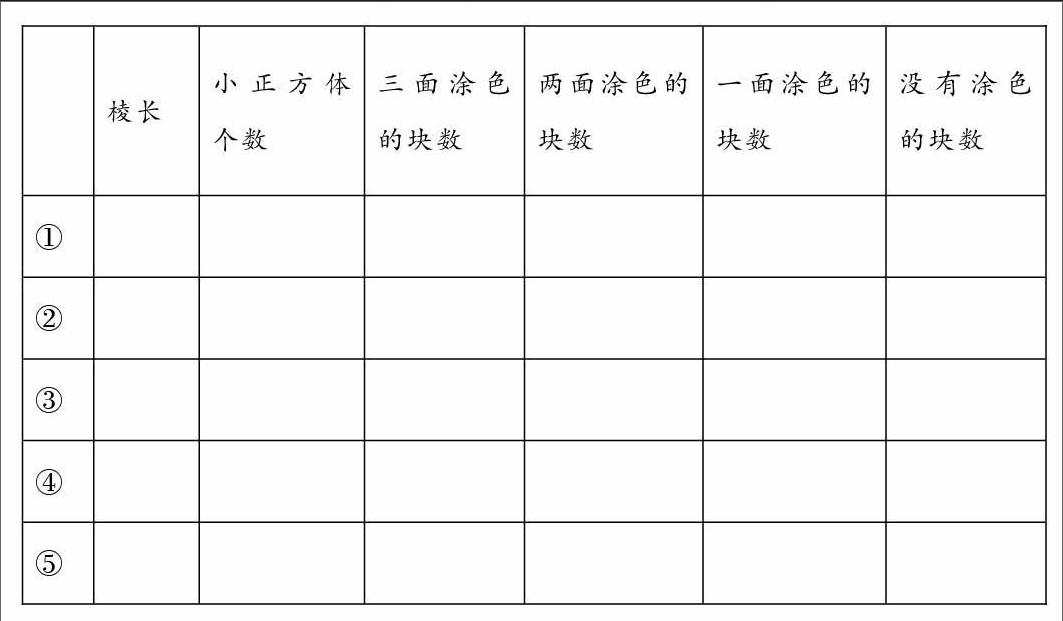
教師出示四階魔方,讓學生認真觀察,并用數學語言描述魔方。學生有的指出它是正方體,有的指出它有6個面、8個頂點、12條棱,還有的發現它是由64個小正方體拼成的。教師繼續設問,64個小正方體拼成的大正方體,它的6個面都涂上了顏色,請想象一下,64個小正方體會有幾個面被涂上顏色?如果根據涂色的情況給這64個小正方體分類,你想怎樣分?學生指出按照涂色的面數可以分為三面涂色、兩面涂色、一面涂色和沒有涂色。每一類小正方體分別有多少個呢?學生一時還算不出來。
教師先引導學生思考:最少用幾個小正方體可以拼成一個稍大的正方體?學生思考后發現至少需要8個小正方體才能拼成一個大正方體。教師用課件出示①號圖形,用8個棱長1cm的小正方體拼成棱長為2cm的大正方體后,把它的表面涂上顏色,請想象一下,這些小正方體會有幾個面被涂上顏色?學生指出3個面后,教師引導學生把要研究的問題及觀察的數據記錄下來并以表格的形式呈現(表格如下)。
接著繼續追問,如果將這個大正方體拼得再大一點,需要多少個小正方體?學生發現需要27個小正方體,也就是用棱長1cm的小正方體拼成棱長為3cm的的大正方體。運用類推的思考方式,接下來是要繼續探究棱長為4cm、5cm、6cm的大正方體中各小正方體表面的涂色規律。
二、分類計數,收集探究材料
教師用棱長1cm的小正方體拼成棱長為3cm的大正方體,把它們的表面分別涂上顏色后問學生:其中三面、兩面、一面涂色的小正方體各有多少個?還有一個正方體是哪一種?學生討論交流后發現,還有一種是六個面都沒有涂色的。在學生填表的過程中,教師追問:三面、兩面、一面和沒有涂色的小正方體分別在正方體的哪個位置?如果拼成棱長為4cm的大正方體后,需要多少個小正方體?其中三面、兩面、一面涂色的小正方體各有多少個?學生借助直觀圖,發現三面涂色的小正方體共8個,在原來大正方體的8個頂點的位置;兩面涂色的共有24個,分別是每一條棱上的中間兩個(此處有學生是數出來的,有學生是用2×12算出來的);一面涂色的共24個,分別是每個面的正中間的4個;沒有涂色的塊數是8個(64-8-24-24=8)。
三、數形結合,推理概括規律
通過前幾次的探究,學生結合圖形發現了如下規律:三面涂色的小正方體都在大正方體的頂點的位置。不論棱長是幾,分割后三面涂色的小正方體的個數都是8個。兩面涂色的小正方體都在大正方體的棱的位置,只要用每條棱中間兩面涂色的小正方體的個數乘12,就得出兩面涂色的小正方體的總個數。一面涂色的小正方體都在大正方體的面的位置,只要用每個面上一面涂色的小正方體的個數乘6,就得出一面涂色的小正方體的總個數。沒有涂色的個數=總塊數-三面涂色的塊數-兩面涂色的塊數-一面涂色的塊數。據此,筆者引導學生探討棱長是5cm、6cm時的涂色規律,學生合作探究后將所得結果填寫在表格中再次驗證了上述發現。如果拓展到一般規律:把棱長為n的大正方體涂色切割,三面涂色、兩面涂色、一面涂色及沒有涂色的塊數的小正方體各有多少個?師生共同歸納得出:三面涂色的在正方體頂點的位置,因為正方體有8個頂點,所以都有8個;兩面涂色的在正方體棱上除去兩端的位置,因為正方體有12條棱,所以有(n-2)×12個;一面涂色的在正方體每個面除去周邊一圈的位置,因為正方體有6個面,所以有(n-2)2×6個;沒有涂色的在正方體里面除去表面一層的位置,所以有(n-2)3個,或者,用總塊數-三面涂色的塊數-兩面涂色的塊數-一面涂色的塊數。
教學中,教師采用小組活動與全班集體活動相結合的形式,放手讓學生用小正方體擺一擺,拿魔方看一看,讓每一個學生都有活動的空間和時間,使學生在數學實踐活動中學會求知、學會合作、學會交流,在活動中獲得了成功的快樂。學生通過探索圖形涂色規律的活動,深化了對正方體特征的認識,不斷拓寬了獲取數學知識的渠道,感受了數學思考的魅力。在探索規律的過程中,教師引導學生初步體會了建立數學模型的過程,即從具體到抽象,從特殊到一般,逐步揭示圖形之間的內在聯系,鼓勵學生用數學語言和模型正確地表達發現的規律。
整節課,充分體現了讓學生親身經歷將實際問題抽象成數學模型并加以解釋與運用的過程,在讓學生根據直觀立體圖形進行推理想象進而歸納出不同涂色面數的小正方體的數量的過程中,提高了學生的空間想象能力。
(作者單位:襄陽市襄州區教研室)

