活性染料三原色泡沫染色配色體系

張曉云, 冒曉東, 趙文杰, 鐘 毅, 徐 紅, 毛志平

(東華大學 a. 化學化工與生物工程學院; b. 生態紡織教育部重點實驗室, 上海 201620)

活性染料三原色泡沫染色配色體系

張曉云a, b, 冒曉東a, b, 趙文杰a, b, 鐘 毅a, b, 徐 紅a, b, 毛志平a, b

(東華大學 a. 化學化工與生物工程學院; b. 生態紡織教育部重點實驗室, 上海 201620)

為探討活性染料三原色泡沫染色配色體系, 采用配伍性良好的雷馬素深紅RGB、金黃RGB、藏青RGB對棉織物進行泡沫染色, 建立了泡沫染色配色基礎數據庫, 研究了泡沫染色配色算法.結果表明, Kubelka-Munk單常數理論方程適合活性染料三原色泡沫染色配色體系研究.由于泡沫拼色染色時染料之間相互會有影響, 在Kubelka-Munk單常數理論方程中引入糾正系數, 可以減小理論K/S值和實測K/S值的偏差.

三原色; 泡沫染色; 活性染料; 測色; 配色; 染色基礎數據庫

泡沫染色是一種新型的低給液、高節能的染色技術.相對于傳統高帶液率(56%～100%)的浸軋方式, 泡沫染整的帶液率為20%～40%.低帶液率加工不僅能顯著降低用水量、化學品耗用量和后期烘燥能源, 而且能夠避免大量的染料水解, 以及在后續烘燥環節由于高帶液率產生的染料“泳移”現象[1-2].因此, 泡沫染色技術的產業化應用對于推動整個染整行業的清潔生產和節能減排具有重要意義[3]. 目前關于泡沫染色的研究大多為單色染色, 棉織物泡沫染色配色研究少有報道[4].研究泡沫染色的配色算法, 并將其應用到計算機配色技術中, 可以節省打樣時間, 提高生產效率, 對于推動泡沫染色技術的產業化應用具有現實意義.Kubelka-Munk函數理論是目前大多數配色軟件的理論基礎, 其單常數理論形式簡單, 易于應用, 常用于紡織印染、皮革染色、印刷油墨拼色配色中[5-6].

在對泡沫染色液體系的發泡性和穩定性以及泡沫染色工藝系統研究[6-9]的基礎上, 本文采用配伍性能良好的雷馬素深紅RGB、金黃RGB和藏青RGB三原色活性染料對棉織物進行泡沫染色拼色, 研究了3支染料泡沫染色染棉織物的配色體系, 修正了泡沫染色配色算法, 為進一步研究泡沫染色計算機配色建立基礎.

1 實驗部分

1.1 實驗材料

織物: 純棉機織半漂布(華紡股份有限公司), 經、緯紗線密度均為25 tex, 經密: 520根/(10cm), 緯密: 280根/(10cm), 面密度為115 g/m2.

試劑: 雷馬素深紅RGB、金黃RGB、藏青RGB(上海德司達印染科技有限公司); 十二烷基硫酸鈉(SDS)(上海精細化工材料研究所, 化學純); 十二醇、無水碳酸鈉(國藥集團化學試劑有限公司, 化學純); 瓜爾膠(鄭州市中原區豐和化工商行, 工業級).

1.2 實驗儀器

泡沫發生器和泡沫施加器(上海技楷機電設備有限公司); UPEI型連續式織物熱定型機(中國臺灣瑞比公司); Model P-BU型電動均勻軋車(中國臺灣Rapid公司); Datacolor 650型測色儀(美國Datacolor公司); UV-1800型紫外分光光度儀(日本Shimadzu公司), SW-12AⅡ型皂洗機(溫州大榮紡織儀器有限公司).

1.3 實驗方法

1.3.1 泡沫染色方法

泡沫染色液的配方: 活性染料為Xg/L; SDS為2.0～8.0 g/L; Na2CO3為15～30 g/L; 十二醇和瓜爾膠用量總和為0.28～0.70 g/L, 其中十二醇和瓜爾膠質量比為3∶4.

設備參數設定: 發泡比為8.0; 液體密度為1.00 g/cm3; 幅寬為0.50 m; 帶液率為35%; 車速為8.0 m/min; 攪拌速度為400 r/min.

泡沫染色工藝流程如圖1所示.

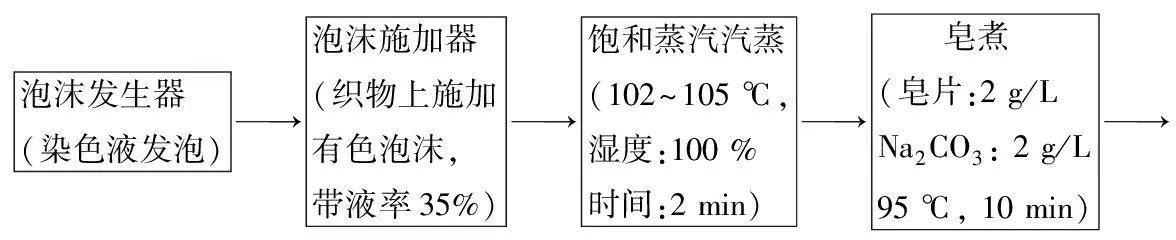
圖1 泡沫染色工藝流程

Fig.1 Foam dyeing process

1.3.2 基礎數據庫的建立

基礎數據庫建立的方法: 按照表1中3種活性染料(雷馬素深紅RGB、金黃RGB、藏青RGB)單色樣分檔質量濃度分別對棉織物進行泡沫染色, 染色完成后利用測色儀對棉織物進行測色, 記錄各測色數據.為保證測量精確度, 測量時應注意: 采用大孔測量(大孔徑為30 mm); 布樣折疊4層以上, 排除背景影響; 每塊布樣取著色均勻的8個不同位置進行測色.

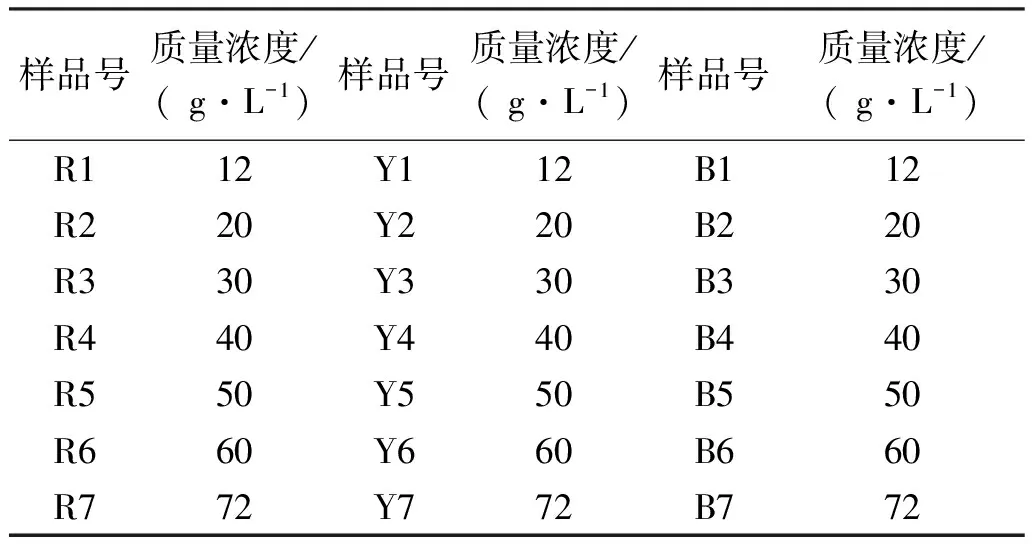
表1 3種活性染料單色樣分檔質量濃度

1.3.3 基礎數據庫的檢驗

完成基礎數據庫后, 需要對數據庫進行檢驗以確保其正確性.在染制不同色樣的過程中, 由于稱料、配液、時間等操作誤差, 可能會造成打樣偏差.因此, 需要檢驗數據庫的正確性, 對有偏差的色樣進行修正, 對于偏差較大的布樣, 應重新進行打樣加以修正[10-11].

(1) 反射率R值與波長λ的曲線圖

在不同單色染料質量濃度下, 染色樣的反射率R值曲線應是有規律的平行分布.染料質量濃度越小, 反射率R值越高; 染料質量濃度越大, 反射率R值越低.若曲線有不規則現象或出現交叉, 則應加以修正.

(2) 表面色深K/S值與波長λ的曲線圖

在不同單色染料質量濃度下, 染色樣的表面色深K/S值曲線應是有規律的平行分布.染料質量濃度越小, 表面色深K/S值越小; 染料質量濃度越大, 表面色深K/S值越大.若曲線有不規則現象或出現交叉, 則應加以修正.

(3) 表面色深K/S值與染料質量濃度C的曲線圖

在低染料質量濃度時, 隨著染料質量濃度的增加, 表面色深K/S值增加; 在高染料質量濃度時, 表面色深K/S值增加速度變慢, 直到纖維達到染色飽和, 表面色深K/S值不再隨染料質量濃度C的增加而增加, 染色達到平衡.若不符合這一規律, 則必須進行修正.

1.3.4 單常數配色算法

計算機配色的基礎理論是Kubelka-Munk函數理論[12-14], 其表達式為

(K/S)=(1-R)2/(2R)

(1)

其中: K為光在不透明介質中的吸收系數; S為光在不透明介質中的散射系數; (K/S)為Kubelka-Munk函數; R為不透明介質的反射率.

假設每個染料分子對光的吸收和散射的程度相同, 則表面色深K/S值應與染料質量濃度成正比.對于染色織物而言, 染料的相對數量較少, 可認為其散射作用由紡織材料所致, 與染料無關, 故僅考慮吸收系數K的變化[15-16], 式(1)可簡化為

(K/S)j=(K/S)t, j+∑iCi·(k/s)t, j

(2)

其中: (K/S)t, j為基底在j波長下的表面色深; (k/s)i, j單常數為質量濃度為Ci的i染料在j波長下的單位濃度表面色深; 在染單色樣時, 即僅存在一種染料, 式(2)可簡化為

(K/S)j=(K/S)t, j+C·(k/s)j

(3)

對于每種染料, 在不同染料質量濃度下染制色樣, 可繪制K/S對C的曲線, 如圖2所示, 以作配色計算使用[10, 14].

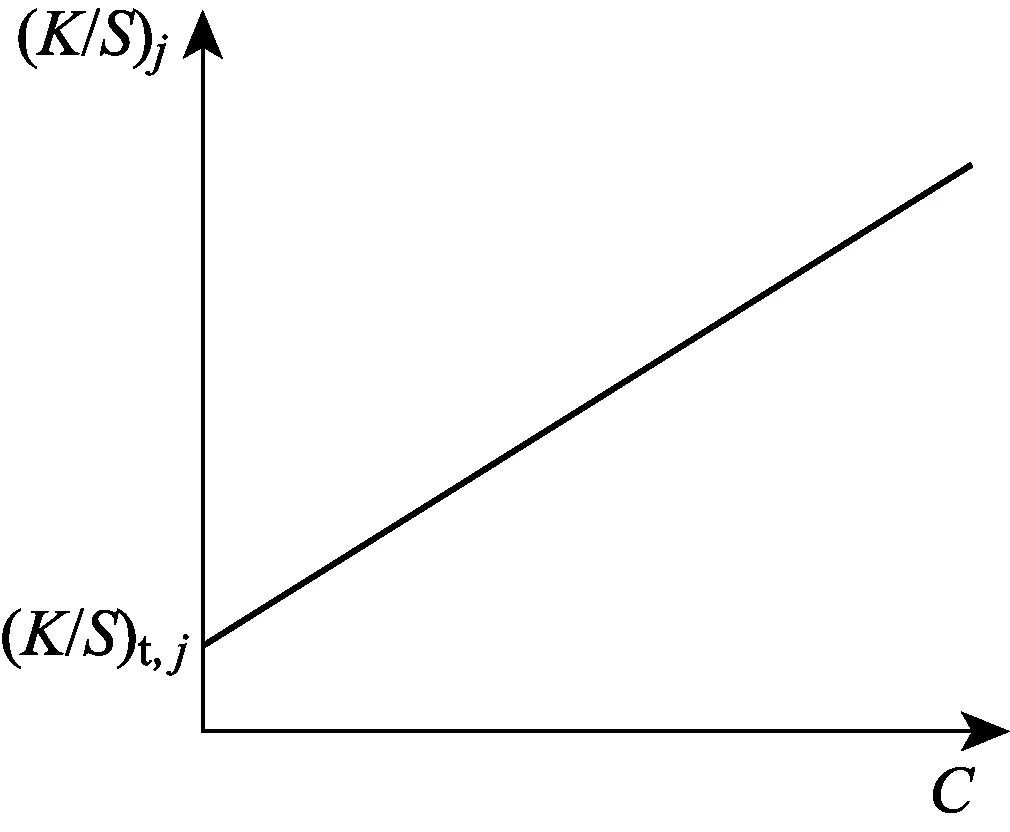
圖2 理論K/S-C曲線Fig.2 The curve of theoretical K/S value and concentration of dyes

由于配色的結果要求配制樣品的(K/S)m值等于標樣的(K/S)s(m代表配制樣品,s代表標樣), 故

(K/S)m=(K/S)s

(4)

2 結果與討論

2.1 單色樣顏色檢驗

2.1.1R-λ曲線

3種活性染料在不同染料質量濃度下的反射率R值隨波長的曲線圖如圖3所示.由圖3可知, 染料質量濃度越大, 反射值R越小; 染料質量濃度越小, 反射值R越高.各單色染料在不同質量濃度下染色樣的反射值曲線呈有規律的平行分布, 無明顯不規則現象或出現交叉.

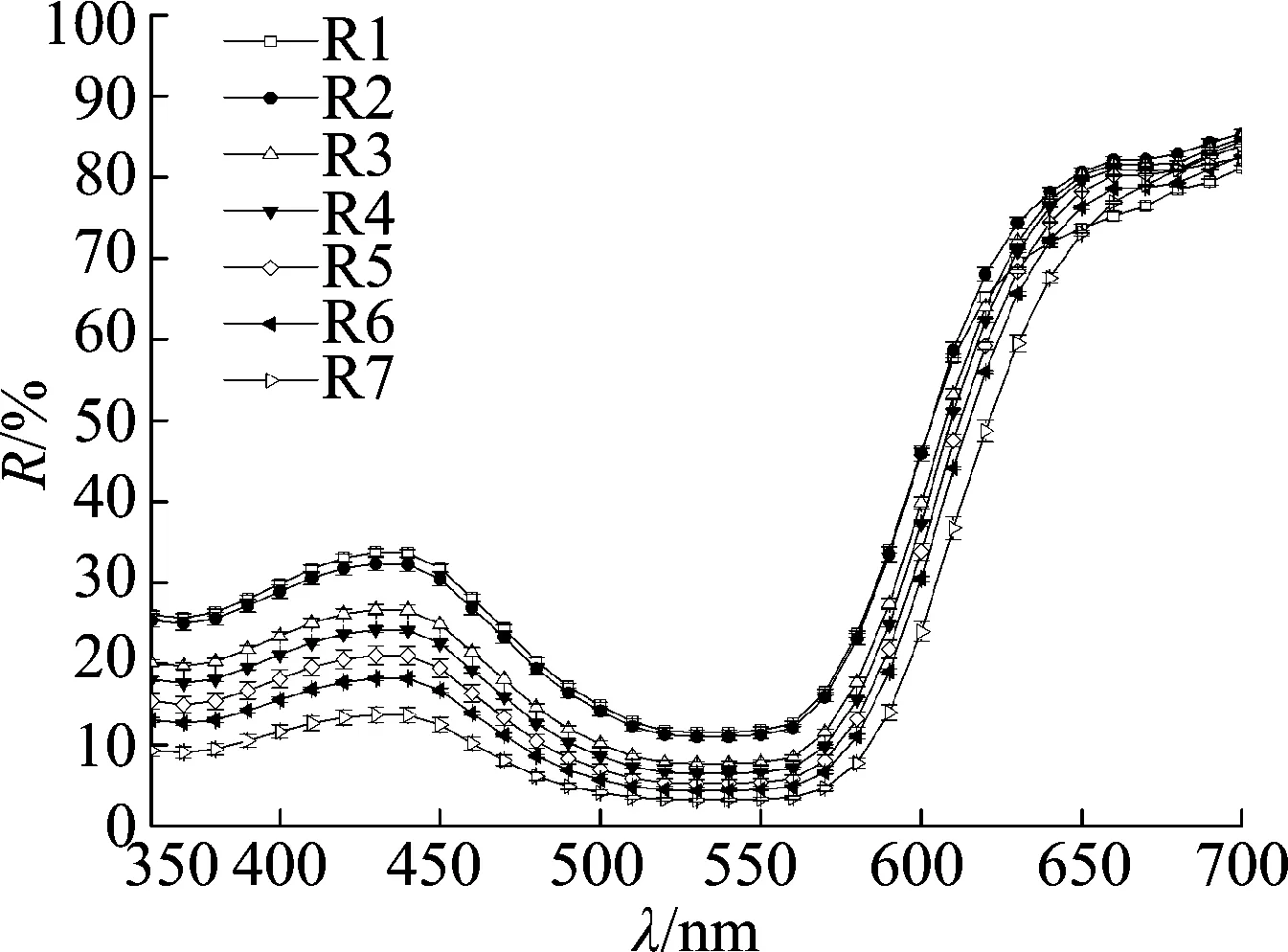
(a) 雷馬素深紅RGB

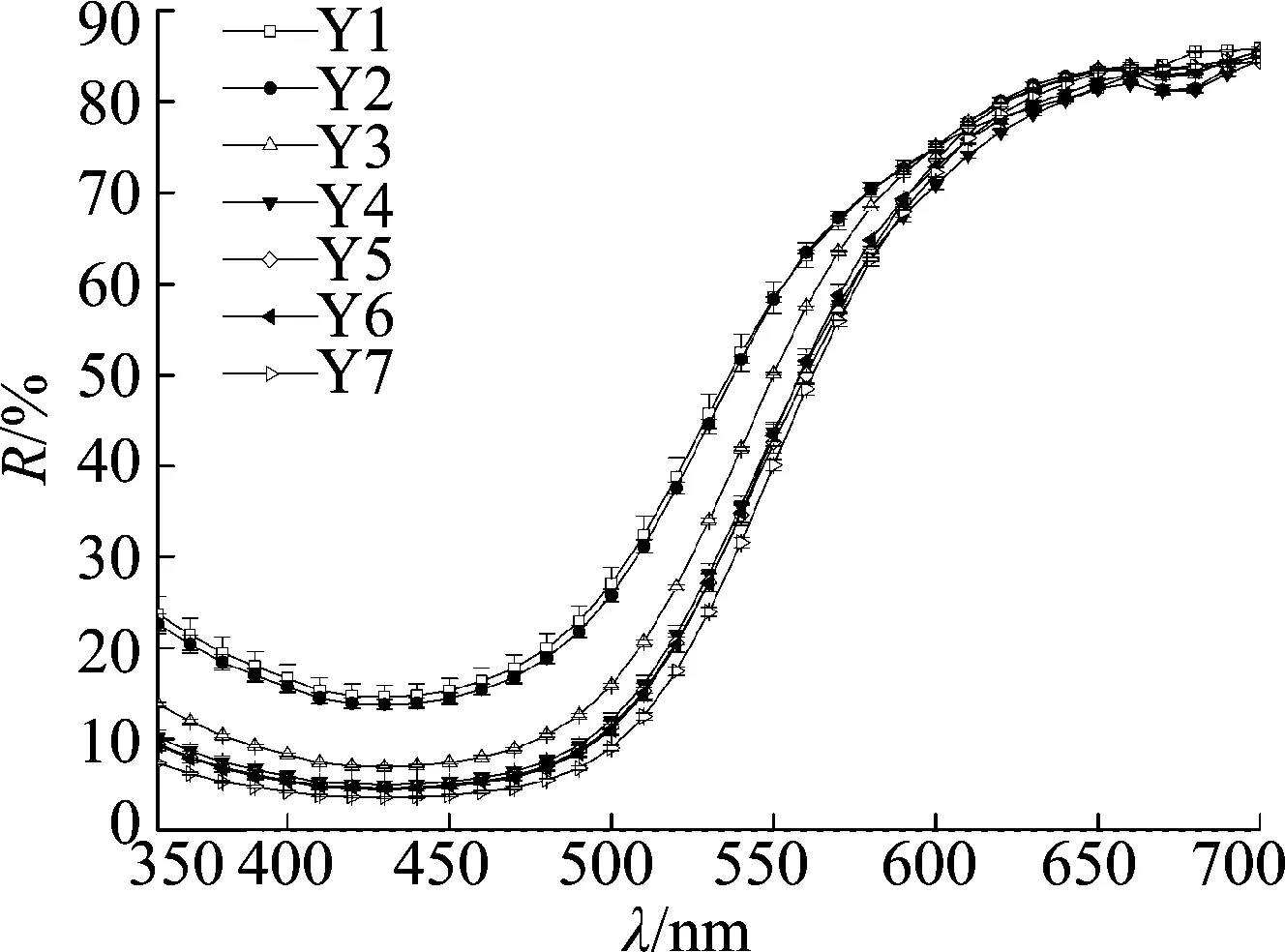
(b) 雷馬素金黃RGB

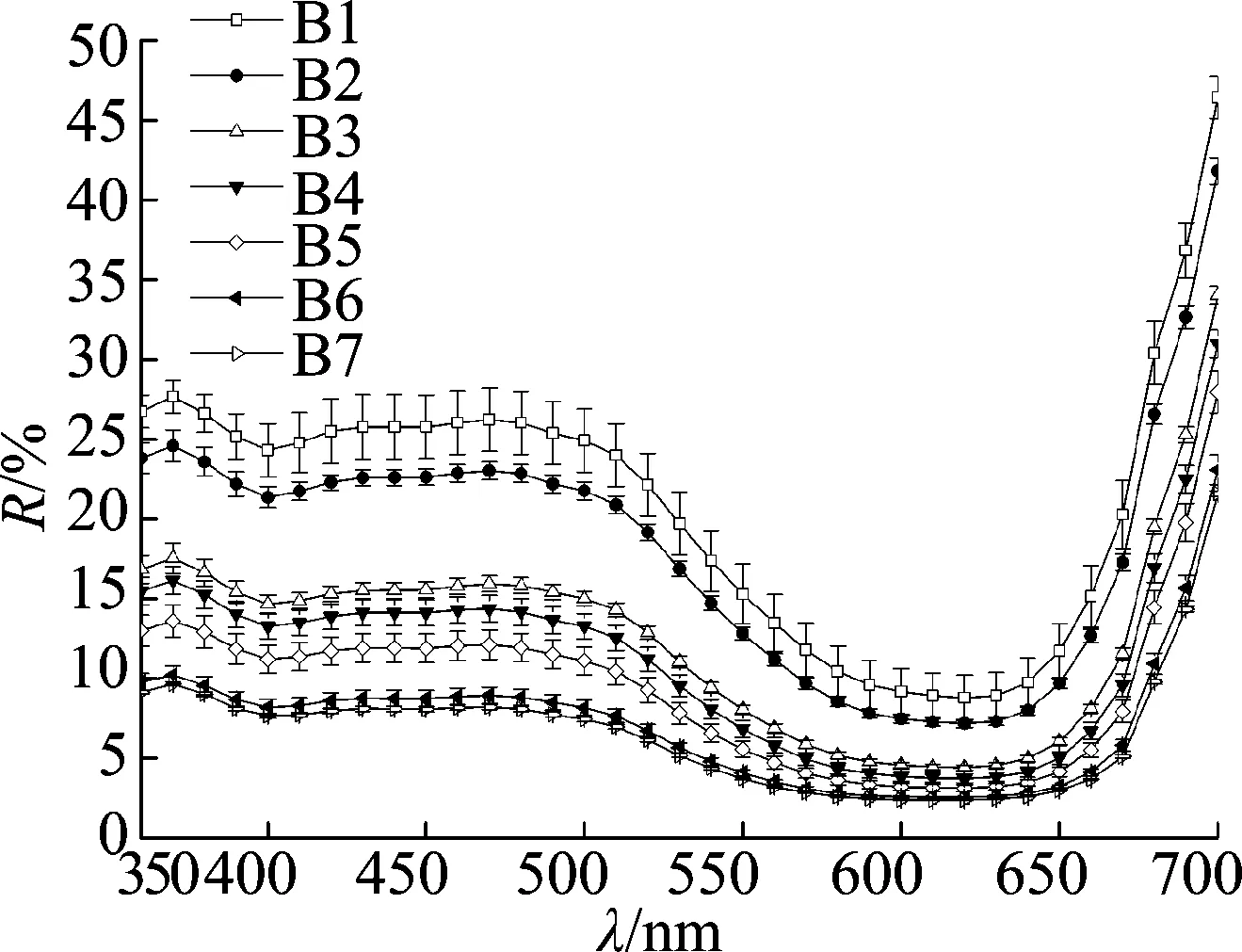
(c) 雷馬素藏青RGB圖3 3種雷馬素RGB活性染料R值與波長λ曲線圖Fig.3 The curve of reflected value and wavelength of three kinds of Remazal RGB? dyes

2.1.2K/S-λ曲線

3種活性染料在不同染料質量濃度下的表面色深K/S值隨波長λ的曲線圖如圖4所示.由圖4可知, 染料質量濃度越大, 表面色深K/S值越大; 染料質量濃度越小, 表面色深K/S值越小.各單色染料在不同質量濃度下染色樣的K/S值與波長λ的曲線呈有規律的平行分布, 無明顯不規則現象或出現交叉.

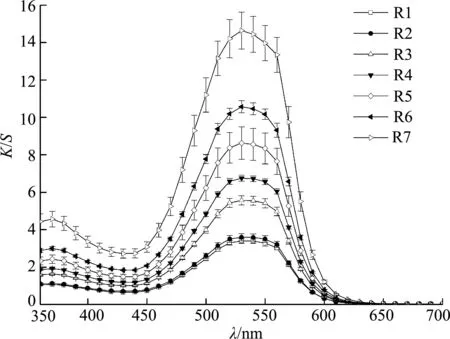
(a) 雷馬素深紅RGB

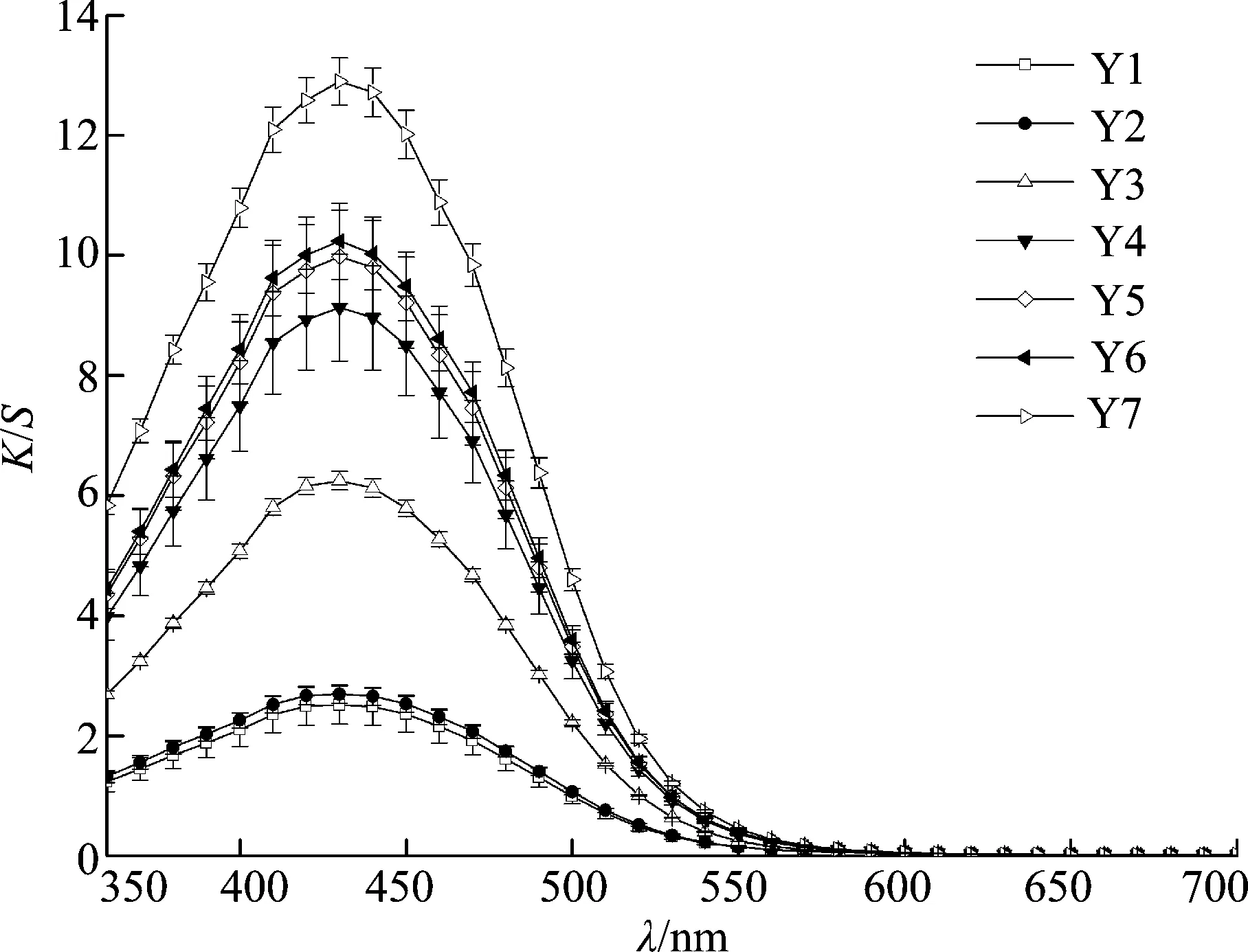
(b) 雷馬素金黃RGB

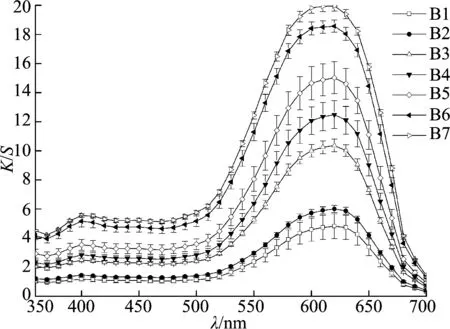
(c) 雷馬素藏青RGB

2.2 單常數配色算法改進

2.2.1K/S-C曲線線性擬合

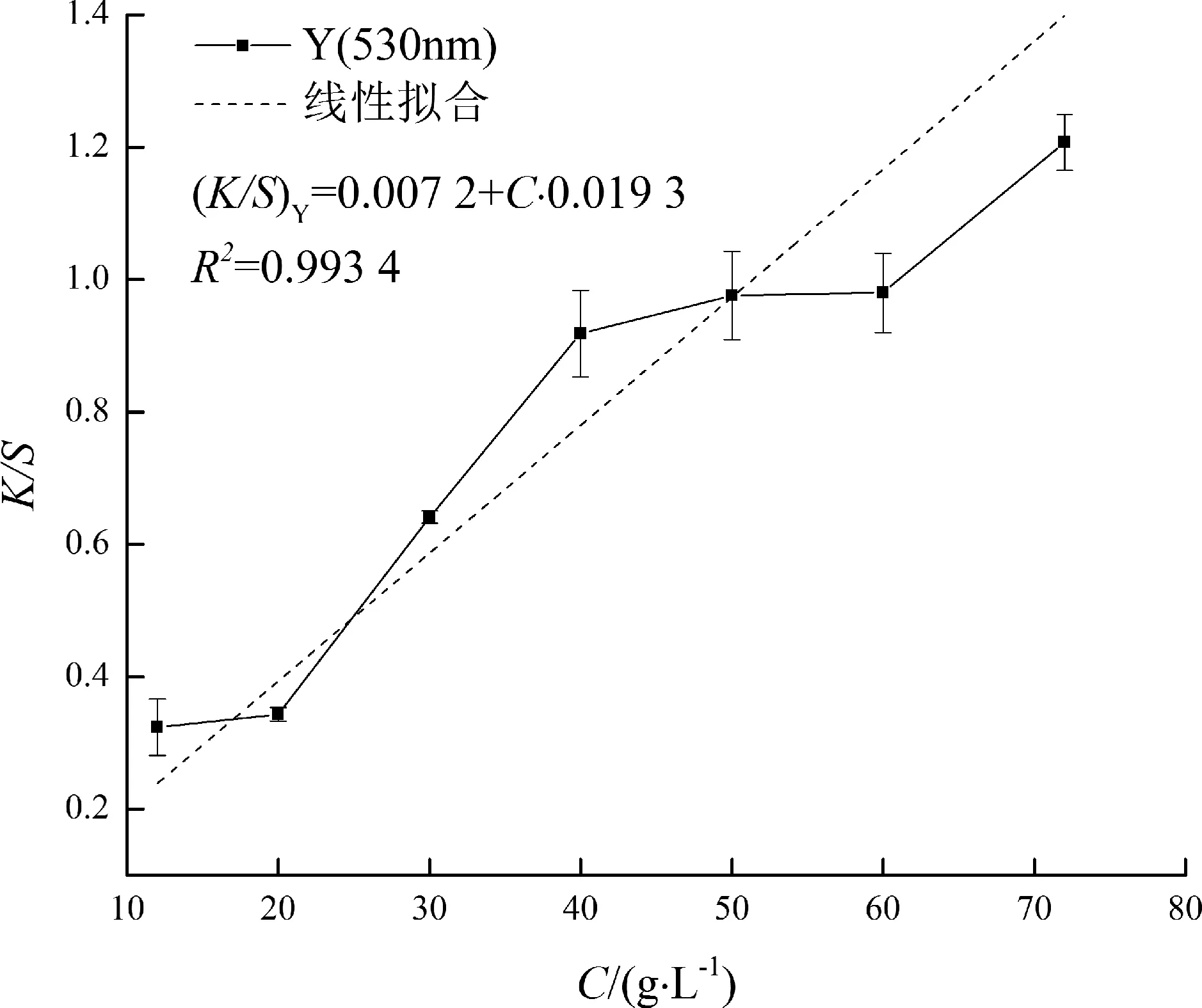
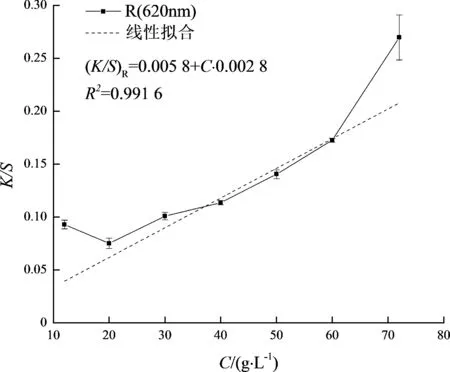
通過課題組前期實驗可知, 雷馬素深紅RGB、金黃RGB和藏青RGB各自最大吸收波長分別是430, 530和620 nm.由3種活性染料在不同波長下的K/S值, 可得K/S-C曲線, 即不同染料質量濃度下各染色樣在最大吸收波長(即反射值最小)處的表面色深K/S值與染料質量濃度C的關系, 分別如圖5～7所示. 利用線性擬合的方法, 可以得到K/S-C的擬合曲線, 得到擬合方程.

(a) 雷馬素深紅RGB

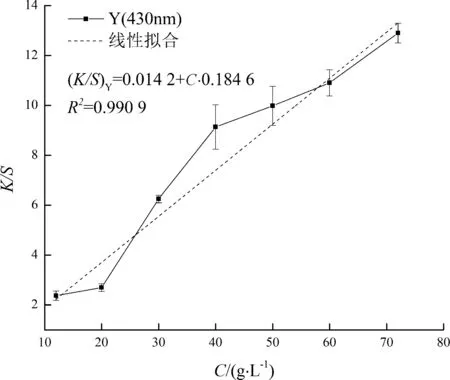
(b) 雷馬素金黃RGB

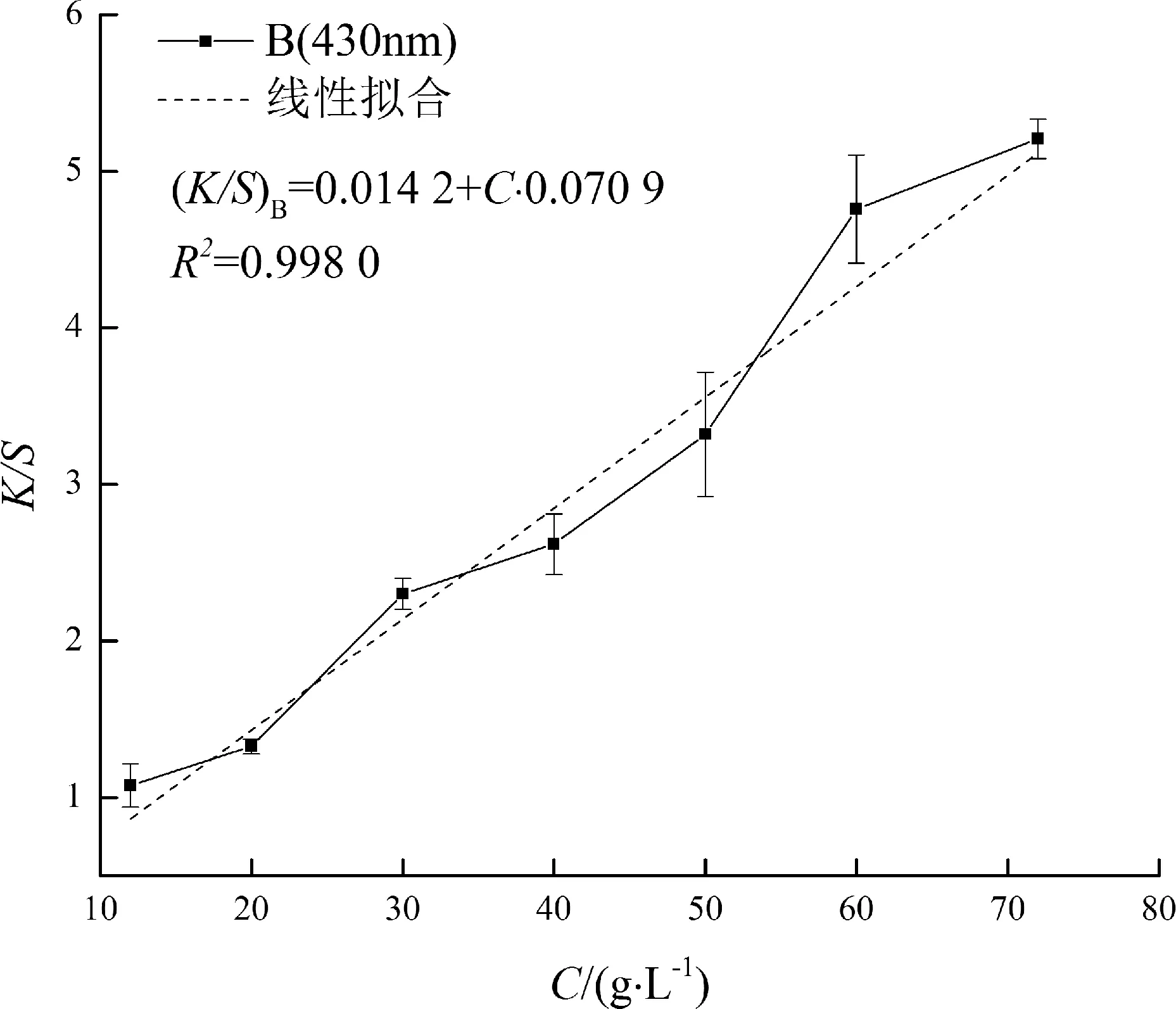
(c) 雷馬素藏青RGB

由圖5可得, 在430 nm下,K/S-C線性擬合方程為

(5)

(a) 雷馬素深紅RGB

(b)雷馬素金黃RGB

(c) 雷馬素藏青RGB

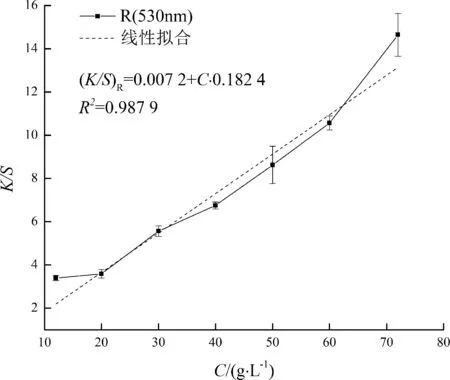
由圖6可得, 在530 nm下,K/S-C線性擬合方程為

(6)

(a) 雷馬素深紅RGB

(b) 雷馬素金黃RGB

(c) 雷馬素藏青RGB

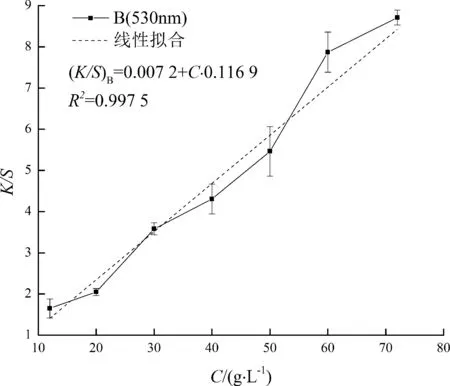
由圖7可得, 在620 nm下,K/S-C線性擬合方程為

(7)

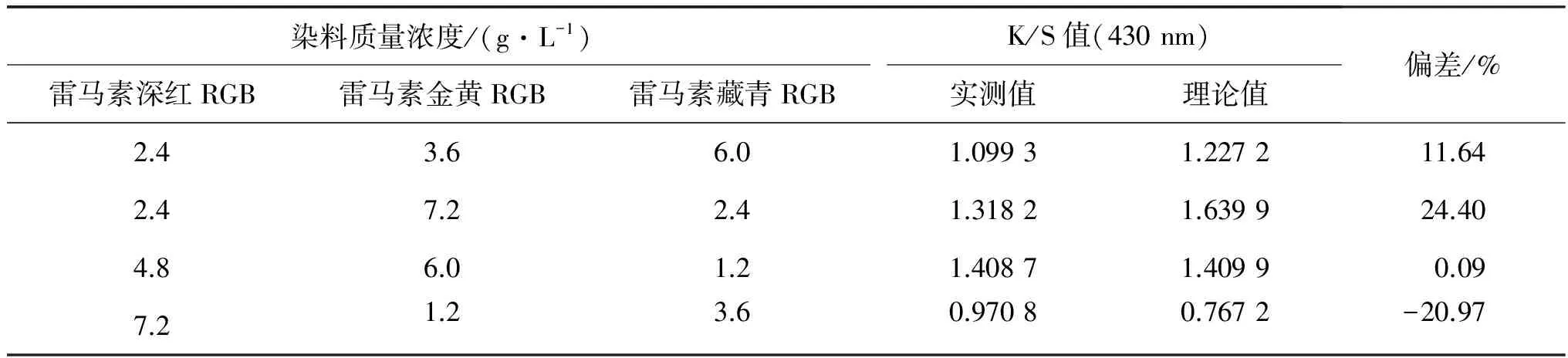
在前期課題組實驗基礎上, 隨機選取不同染色布樣, 根據式(2)和式(5)～(7), 分別計算出在430, 530和620 nm處的理論K/S值, 與實測K/S值作比較, 結果如表2～4所示.

表2 430 nm下不同染料質量濃度染色K/S值的理論值與實測值

(續 表)

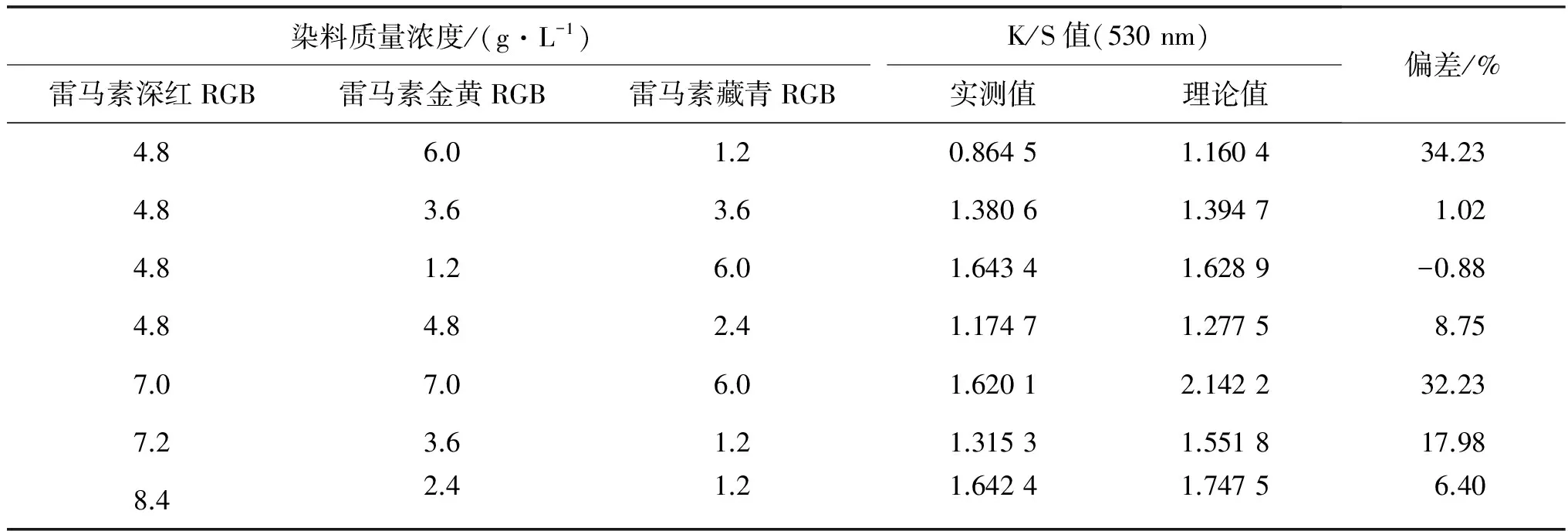
表3 530 nm下不同染料質量濃度染色K/S值的理論值與實測值

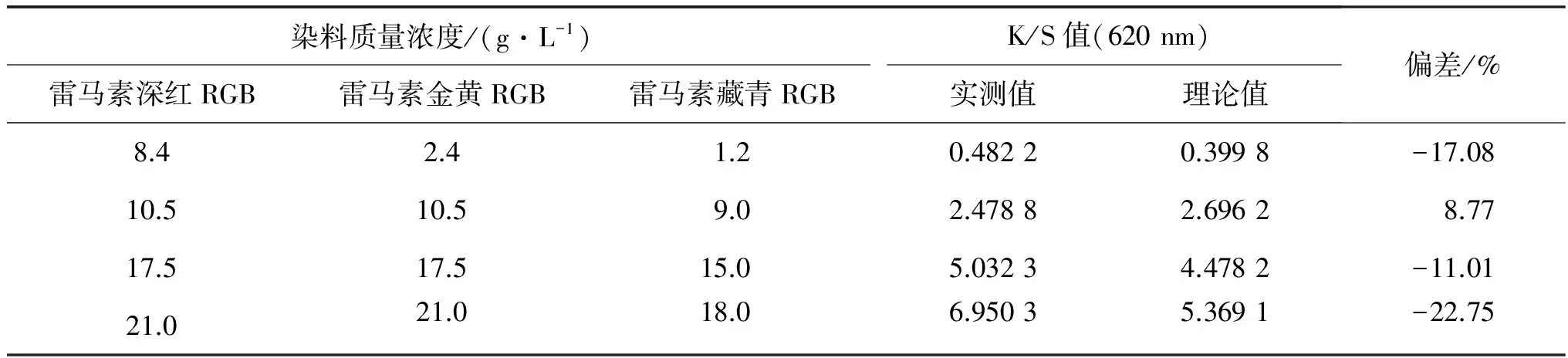
表4 620 nm下不同染料質量濃度染色K/S值的理論值與實測值

由表2～4可知, 利用單常數配色算法的理論方程式得到的理論K/S值和實測K/S值的偏差較大.造成誤差的兩個主要原因: 一是纖維存在表面反射; 二是染色時染料沒有完全上染到纖維上, 即隨著染料濃度的增大, 纖維已達到染色飽和.因此, 活性染料泡沫染色染棉并不完全符合Kubelka-Munk單常數理論, 可通過對K/S值與質量濃度C的關系曲線進行適當的數學處理, 以減小偏差.

2.2.2 引進調整系數

從理論上來講, 染色樣品的K/S值與染料質量濃度C之間關系, 其圖形應是一條直線, 即

Φ=[K/S-(K/S)t]/C

(8)

由于拼色上染時, 混合染料之間相互產生影響.實際上, 從圖5～7知雷馬素深紅RGB、金黃RGB、藏青RGB在各自最大吸收波長處的提升力曲線并不呈直線關系, 往往是凹向下方的曲線.為提高準確度, 可采用引進調整系數的方法來調整曲線凹凸.采用多項式擬合的方法對K/S-C關系曲線進行修正[14], 如式(9)所示.

K/S=a0+a1·C+a2·C2+a3·C3

(9)

其中: 常量a0為基質的(K/S)t; a1近似地代表單位染料質量濃度的表面色深K/S值; 常量a2和a3用來修正曲線的凹陷.考慮到可修正的幅度大小, 一般不需要使用高于三階的多項式進行修正.

在Matlab中采用最小二乘擬合得到, 雷馬素深紅RGB、金黃RGB、藏青RGB在波長430 nm下K/S值與染料質量濃度C的方程為

(10)

其中: (K/S)R, (K/S)Y, (K/S)B分別表示雷馬素深紅RGB、金黃RGB、藏青RGB的K/S值; CR, CY, CB分別表示雷馬素深紅RGB、金黃RGB、藏青RGB的質量濃度.

由式(2)和(10)可以計算得到波長430 nm時的理論K/S值, 與實測K/S值作比較, 如表5所示.

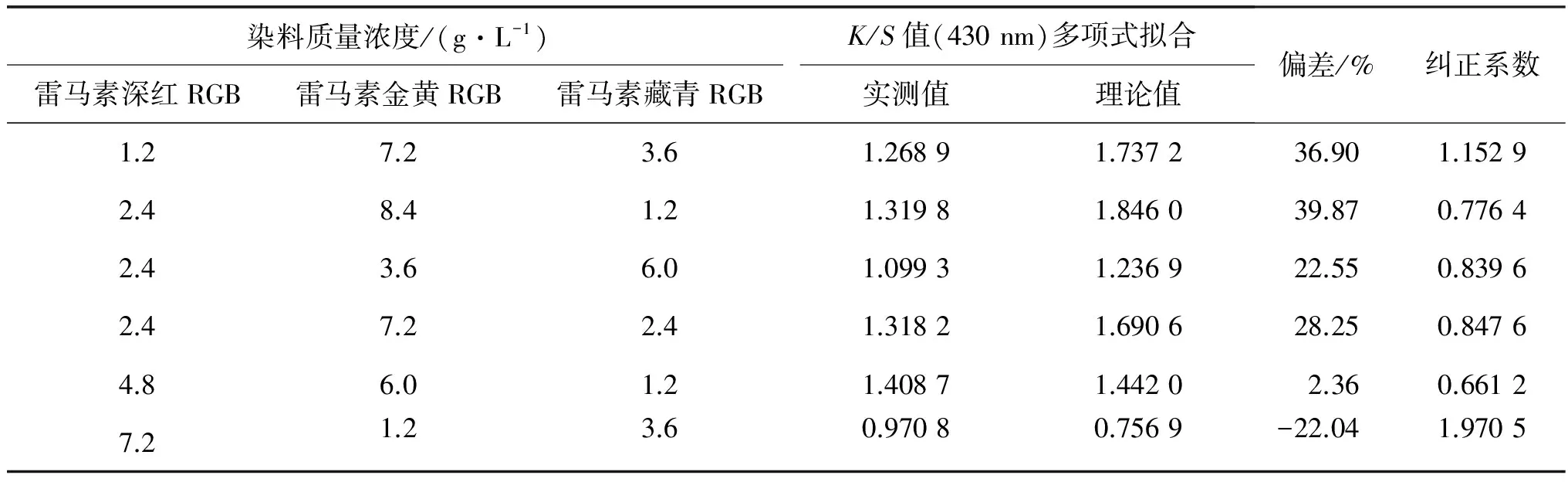
表5 430 nm下不同染料濃度染色調整K/S值的理論值與實測值

同理, 利用Matlab可以得到530 nm下的K/S值與染料質量濃度C的方程為

(11)

由式(2)和(11)可以計算得到波長530 nm時的理論K/S值, 與實測K/S值作比較, 如表6所示.

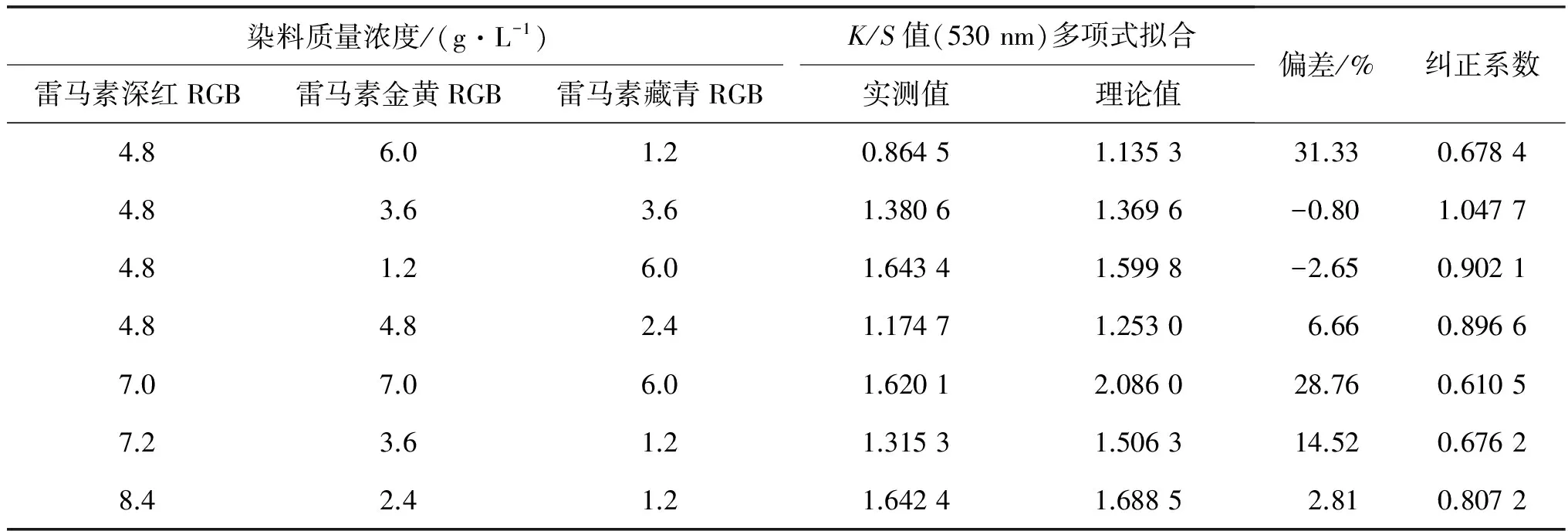
表6 530 nm下不同染料濃度染色調整K/S值的理論值與實測值

同理, 利用Matlab可以得到620 nm下的K/S值與染料質量濃度C的方程為

(12)

由式(2)和(12)可以計算得到波長530 nm時的理論K/S值, 與實測K/S值作比較, 如表7所示.

表7 620 nm下不同染料濃度染色調整K/S值的理論值與實測值

2.2.3 引入糾正系數

由于混合染料拼色上染時, 某一種染料在最大吸收波長處測得的K/S值會受到另外兩種染料的影響, 為了糾正K/S理論值與實測值的偏差, 考慮引進糾正系數k, 以減小拼色染色時染料間的互相影響[17-19].雷馬素深紅RGB的糾正系數的計算方法為

(13)

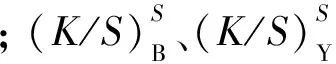
同理, 雷馬素金黃RGB和雷馬素藏青RGB的糾正系數分別為

(14)

(15)

為確定糾正系數與另外兩種染料用量間的關系, 考慮用Matlab軟件做多元線性回歸, 得到如下方程[17-19]:

kY=0.239 5+0.149 5·CR+0.097 8·CB

(16)

kR=0.957 5-0.044 5·CY+0.008 7·CB

(17)

kB=0.539 6+0.104 1·CR-0.068 8·CY

(18)

在Kubelka-Munk單常數理論方程中引入糾正系數, 則在三拼色染色過程中[9, 18-19]有

(K/S)m=(K/S)w+kY·(K/S)Y+

kB·(K/S)B+kR·(K/S)R

(19)

由式(16)～(19)可得各波長下的糾正理論K/S值, 與實測值對比, 如表8～10所示.

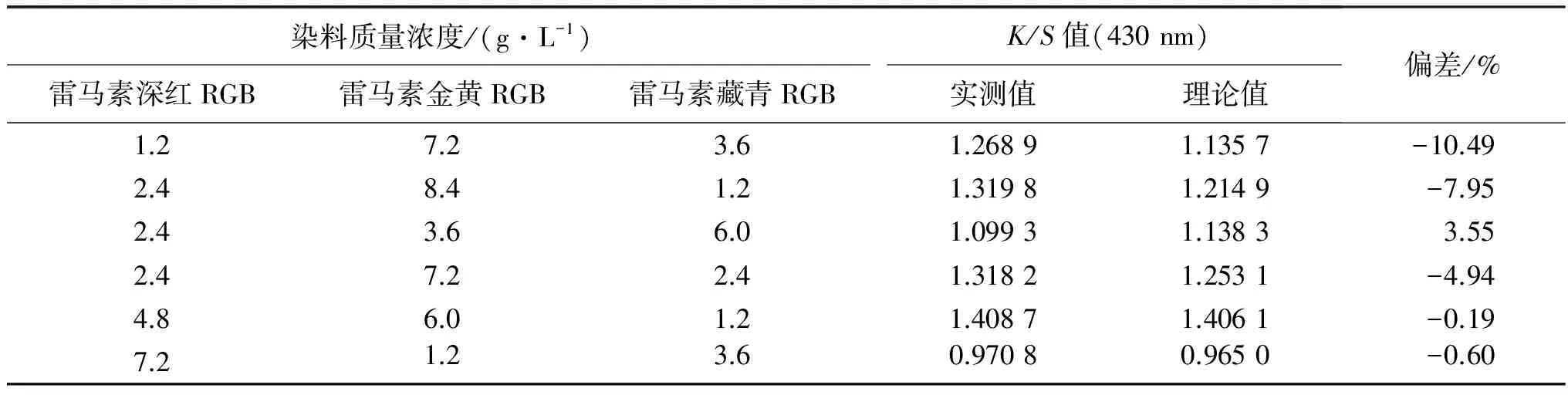
表8 430 nm下不同染料濃度染色糾正K/S值的理論值與實測值

表9 530 nm下不同染料濃度染色糾正K/S值的理論值與實測值

(續 表)

表10 620 nm下不同染料濃度染色糾正K/S值的理論值與實測值

由表8～10可知, 在Kubelka-Munk單常數方程中引入糾正系數得到的理論K/S值與實測K/S值的偏差較糾正前的偏差小, 且偏差基本可以降低到10%以下.考慮將得出的Kubelka-Munk糾正方程用于泡沫染色計算機配色數據庫, 可以減小色差.

3 結 論

(1) 建立完成染料數據庫之后進行測配色, 通過檢驗R值與波長λ的曲線圖、K/S值與波長λ的曲線圖和K/S值與質量濃度C曲線圖確定染料基礎數據庫是否正確.如有偏差, 需對異常色樣進行修正或重新打樣.

(2) 活性染料混拼泡沫染色時, 由于染料之間相互有影響, Kubelka-Munk單常數理論方程計算出的理論K/S值與實測K/S值有較大偏差; 通過在Kubelka-Munk單常數理論方程中引進調整系數可以減小理論K/S值與實測K/S的偏差; 通過引進糾正系數可以將理論K/S值和實測K/S值的偏差降低到10%以下.

致謝

感謝上海技楷機電設備有限公司提供泡沫連續染色試樣機.

[1] 趙濤．染整工藝學教程 [M]．北京: 中國紡織出版社, 2005: 15-16．

[2] 陳立秋．泡沫染整技術的節能 [J]．染整技術, 2010, 32(9): 49-55．

[3] 葉早萍．突破耗能桎梏的泡沫整理 [J]．印染, 2010(10): 55-56．

[4] 余弘．活性染料對棉織物的泡沫染色及其固色機理 [D]．上海: 東華大學化學化工與生物工程學院, 2015．

[5] RAVICHANDRAN P． Review of computer colourant formulation [J]．Colourage, 2001, 48(7): 25-30．

[6] ROY S B, MAHNAZ M．Single-constant simplification of kubelka-munk turbid-media theory for paint systems-a review [J].Color Research & Application, 2007, 32(3): 201-207．

[7] YU H, WANG Y F, ZHONG Y, et al．Foam properties and application in dyeing cotton fabrics with reactive dyes [J].Coloration Technology, 2014, 130(4): 266-272．

[8] 譚思思．活性染料泡沫染色技術研究 [D]．上海: 東華大學化學化工與生物工程學院, 2013．

[9] 王元豐．棉織物活性泡沫染色技術 [D]．上海: 東華大學化學化工與生物工程學院, 2014．

[10] 黃利利．分散染料微膠囊測配色體系初探 [D]．上海: 東華大學化學化工與生物工程學院, 2007．

[11] 薛朝華, 賈順田, 李楨．電腦測色配色系統在錦綸織物染色中的應用研究 [J]．陜西科技大學學報, 2005, 23(4): 49-55．

[12] KUBELKA P, MUNK F．Ein beitrag zur optik der farbanstriche[J]．Z Tech Physik, 1931, 12(5): 593-595．

[13] 金福江, 湯儀平．計算機配色中活性染料單位濃度K/S值研究 [J]．武漢理工大學學報, 2008, 30(1): 83-92．

[14] 許海松．顏色技術原理及在印染中的應用(十六)[J]．印染, 2006(9): 36-38．

[15] 張文化, 鄭榮興．活性染料染色數據庫的建立與應用 [J]．印染, 2009(5): 18-20．

[16] ALEXANDER A K．Physical interpretation and accuracy of the Kubelka-Munk theory [J]．Journal of Physics D: Applied Physics, 2007, 40(7): 2210-2216．

[17] 蓋恒軍．紙箱板計算機配色系統的開發 [D]．天津: 天津科技大學材料與化工學院, 2004: 23-27．

[18] 左津梁, 黃崗, 邢彥軍, 等．超臨界CO2介質染色的分散染料拼色性能 [J]．印染, 2010(6): 10-14．

[19] 左津梁．分散染料三原色在超臨界CO2中對滌綸染色的拼色研究 [D]．上海: 東華大學化學化工與生物工程學院, 2010．

Color Matching System for Trichromatic Reactive Dyes in Foam Dyeing

ZHANGXiao-yuna, b,MAOXiao-donga, b,ZHAOWen-jiea, b,ZHONGYi*a, b,XUHonga, b,MAOZhi-pinga, b

(a. College of Chemistry, Chemical Engineering and Biotechnology; b. Key Laboratory of Science &Technology of Eco-Textile, Ministry of Education, Donghua University, Shanghai 201620, China)

In order to investigate the color matching system for trichromatic reactive dyes in foam dyeing, Remazal Red RGB, Remazal Yellow RGB and Remazal Navy RGB had been used to dye bleached cotton fabric. The establishment of basic database for trichromatic reactive dyes in foam dyeing and their verifying methods in color matching were detailed. The results show that the Kubelka-Munk theory with single constant can meet the requirement of foam dyeing color matching. Owing to the interactions among mixed dyes in foam dyeing, the introduction of corrective coefficient to revise Kubelka-Munk theory with single constant can reduce the deviation of theoreticalK/Svalue and measuredK/Svalue.

trichromatic; foam dyeing; reactive dyes; color measurement; color matching; dyeing database

1671-0444 (2016)06

2015-07-31

國家科技支撐計劃資助項目(2014BAE01B01，2014BAC13B02)；上海市聯盟計劃資助項目(LM201439)

張曉云(1989—)，女，河北邯鄲人，碩士研究生，研究方向為活性染料泡沫染色.E-mail：didi-elva@foxmail.com 鐘 毅(聯系人)，女，講師， E-mail：zhongyi@dhu.edu.cn

TS 193.5

A