解常微分方程程序的蛻變測試方法*

邱舒婷 張志祥

(海軍工程大學計算機工程系 武漢 430033)

解常微分方程程序的蛻變測試方法*

邱舒婷 張志祥

(海軍工程大學計算機工程系 武漢 430033)

數值計算方法被廣泛運用于實際生活中,解微分方程問題則是數值計算問題中的一個重要分支,但由于求解微分方程的程序很難直接找到一個測試Oracle來驗證程序的有效性,進而提出用蛻變測試方法檢測解微分方程程序的有效性。通過對解常微分方程的典型程序測試的案例分析,提出了一種求解常微分方程程序的蛻變測試方法,最后進行一個實例驗證該方法的有效性。

數值計算;微分方程;蛻變測試;Oracle問題

(Department of Computer Engineering, Naval University of Engineering, Wuhan 430033)

Class Number TP311

1 引言

數值計算程序對我們的日常生活非常重要,不僅廣泛運用于各種理論學科中,還在動力工程和醫學實踐中的任務關鍵型和安全關鍵型應用中有所體現。

由于數值計算中一些不可避免的截斷誤差,取整誤差以及計算進程中的傳播誤差會影響到最終結果,并且找不到一種確切的解法來解決這個問題,因此在很多情況下,測試人員很難甚至是不能得出程序的預期輸出,進而無法將程序的輸出結果與預期結果相比較,這就是軟件測試中常說的Oracle問題[2]。據此,人們提出三種測試方法來為數值計算程序提供一個可選的Oracle[1]：

1) 靜態檢查,進行代碼走查檢驗程序。

2) 動態執行,比較不同的數值計算程序生成的結果。

3) 利用不同的參數設置和輸出結果的一致性來運行該軟件。

運用代碼走查的方法檢驗程序只適用于程序代碼量并不多的情況,但在復雜程序中此法效率很低。即使可以檢測到一些數值解和實驗結果之間的差異,也很難去驗證它們是由于程序bug還是在物理建模中的錯誤引起的。并且在實際情況中,不同的環境設置可能會導致不同的結果。為解決這種Oracle問題,Chen等提出了蛻變測試技術[1]。

在運用蛻變測試技術解決數值計算軟件測試中遇到的Oracle問題上,Tse T H等利用網格精度的不同對偏微分方程程序的執行結果有不同的影響構造出一條蛻變關系,測試了一個狄利克雷邊界條件下的橢圓型偏微分方程程序[3],實驗表明網格精度越高,暴露出程序錯誤的可能性越大,但在不同網格精度中產生的相對誤差值也十分近似,因此適用范圍較為局限。

姚奕等利用蛻變測試技術求解直角坐標系上的圖形面積來對面向整數錯誤檢測的蛻變測試方法進行實例研究[4]。測試發現由于整型錯誤產生的隱錯,實驗結果顯示基于蛻變關系的整型錯誤檢測方法可檢測出平時發現不了的隱式非預期輸出,有效地提高了檢測整型錯誤的效率[11]。

由此可見,相較于一般的測試方法,蛻變測試技術在數值計算軟件測試中能夠更有效地檢驗復雜數值計算程序的正確性。

在數值計算問題的眾多分支中,微分方程數值解法占有重要的地位。它以數值代數和逼近論等學科為基礎,并反過來推動這些相關學科的發展,在科學計算、工程技術等領域有著極其廣泛的運用[5]。但微分方程的數值解法根據微分方程的不同類別各不相同,且很難直接得出其預期結果,而蛻變測試技術在測試微分方程數值計算程序中運用還不是很廣泛,本文將研究用蛻變測試(Metamorphic Testing,MT)技術來緩解數值計算程序中的Oracle問題。

2 相關定義

2.1 蛻變測試相關定義

定義1 蛻變關系(Metamorphic Relation,MR)。假設程序P是用于計算函數f的,f：X→Y在定義域為X,值域為Y上的函數。假設f滿足關系Rf,且關系Rf滿足當f的n組輸入為x1,x2,…,xn∈X(n>1)時,對應的一系列函數輸入結果分別為f(x1),f(x2),…,f(xn)∈Y。這種關系Rf稱為關于f的一條蛻變關系。因此,若程序P是正確的,那么它一定滿足推導式(1)：

R(I1,I2,…,In) =Rf(P(I1),P(I2),…,P(In))

(1)

式中：I1,I2,…,In是程序P對應于x1,x2,…,xn的實際輸入,P(I1),P(I2),…,P(In)則是對應的輸出結果。

以正切函數為例。對于任意兩個輸入x1和x2,滿足x2=π+x1時,一定有tanx2=tanx1。這種關系即可視為一條蛻變關系：

Rtan：x2=π+x1→tanx2=tanx1

(2)

因此在進行測試時,可通過驗證式(1)、(2)的成立與否來驗證程序P的輸出結果正確與否。

定義2 蛻變測試(Metamorphic Testing,MT)。蛻變測試是一種利用未暴露程序錯誤的成功測試用例衍生出后續測試用例,并用衍生測試用例驗證是否滿足程序的某些必要屬性來判斷程序正確性的技術。

測試人員通常會先在原始程序中植入一個變異,再利用蛻變關系生成衍生測試用例進行程序測試。若程序未支持在該蛻變關系下應滿足的屬性,則說明程序存在變異[8]。

2.2 常微分方程的數值計算

定義3 龍格庫塔法(Runge-Kutta)：龍格庫塔法[6]是一種在工程上應用廣泛的高精度單步算法,用于數值求解微分方程。對于一階精度的拉格朗日中值定理有：

對于微分方程：y′=f(x,y)即y(i+1)=y(i)+h*k1,k1=f(xi+yi)。

當用點xi處的斜率近似值k1與右端點xi+1處的斜率k2的算術平均值作為平均斜率k*的近似值,那么就會得到二階精度的改進拉格朗日中值定理：

y(i+1)=y(i)+[h*(k1+k2)/2]

k1=f(xi+yi)

k2=f(x(i)+h,y(i)+h*k1)

依次類推,如果在區間[xi,xi+1]內多預估幾個點上的斜率值k1,k2,…,km,(m>1)并用它們的加權平均數作為平均斜率k*的近似值,顯然能構造出具有很高精度的高階計算公式。經數學推導與求解,可以得出四階龍格庫塔公式,也就是在工程中應用廣泛的經典龍格庫塔算法：

y(i+1)=y(i)+[h*(k1+2*k2+2*k3+k4)/6]
k2=f(x(i)+h/2,y(i)+h*k1/2)
k3=f(x(i)+h/2,y(i)+h*k2/2)
k4=f(x(i)+h,y(i)+h*k3)

2.3 常微分方程求解示例

在實際工作中,解決一項現實問題需要成千上萬個微分方程組,人工求解微分方程的通解是很不現實的,所以微分方程的數值解顯得尤為重要。

在此以一個一階非線性常微分方程(3)為例,給出初始條件當x0=1時,y0=1且x∈[1,6]。

(3)

假設用“四階龍格庫塔法”解上述常微分方程問題。在給定邊界條件和步長h的情況下,程序可以計算出每隔h步長后的x和y的值直到迭代結束[7]。為說明蛻變測試的有效性,我們會在解常微分方程的程序中植入一個變異。圖1是原始程序的關鍵代碼。

圖1 關鍵代碼圖

假設通過將上述程序中的第7行代碼:

k2=(*pfunc)(x0+h/2,y0+k1*h/2)

替換為：

k2=(*pfunc)(x0+h/2,y0-k1*h/2)

來植入一個變異[10],并將設計的該變異程序版本記為Mutant1。將上述原始和植入錯誤的程序編譯執行后,得到的運行結果趨勢如圖2所示。

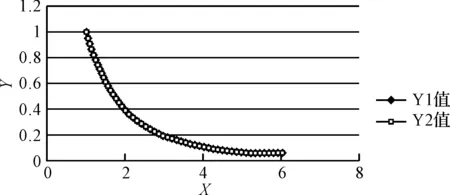
圖2 非線性原始和變異程序運行結果圖

從上述原始和植入變異過后的程序結果中可以看出,兩個程序的輸出值幾乎重合,說明兩個程序的運行結果十分相似。隨著x值的逐步增大,y值逐漸遞減,且最終的y100值變異的運行結果和原始結果相差甚微。因此,當這種問題出現在實際應用中時,我們就很難發現錯誤的存在。

3 解一階非線性常微分方程的蛻變測試方法

由于無法通過一般運算求得一階非線性常微分方程的通解,進而無法構造出程序的預期輸出,待測程序缺乏測試Oracle,因此直接檢測出程序中是否存在錯誤是有一定難度的。

通常在一般的一階常微分方程求解問題中,討論一階非線性常微分方程u′=f(t,u)的絕對穩定性*絕對穩定性：不管在理論還是應用方面,單步法和多步法都必須是穩定的。但這種穩定有兩方面的限制：一是要求h∈(0,h0)充分小,而實際用的h∈(0,h0)都是固定的；二是只允許初值有誤差,往后各步計算都精確,而實際計算時每步都可能有舍入誤差,為了控制這種誤差的增長,需對多步法提出進一步要求,即絕對穩定性。非常困難,因而通常考慮它在解u臨近的線性化方程,即簡化成討論一種簡單的線性常微分方程u′=a*u的絕對穩定性,其中a為實數或復數。

由此引申,由于在用蛻變測試檢測程序的有效性時,檢測一階非線性常微分方程u′=f(t,u)的有效性難度很大,同樣可以考慮檢測u臨近的線性化方程u′=a*u的有效性。為解決上述無法檢測出原始程序中的變異問題,提出基于檢測一階非線性微分方程有效性的蛻變測試一般方法,如圖3所示。

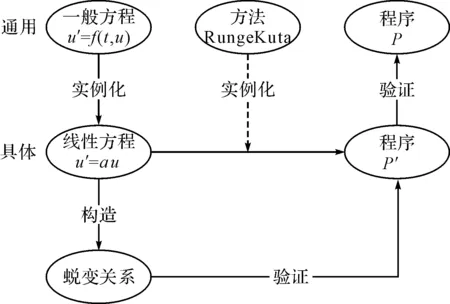
圖3 基于一階非線性微分方程的蛻變測試一般方法

蛻變檢測一階非線性常微分方程的一般方法步驟描述如下：

1) 對于一個一般的一階非線性常微分方程y′=f(x,y),必定存在一個解該方程的一般方法Runge-Kuta,此處以四階龍格庫塔法為例,將方法Runge-Kuta對應的解一階非線性常微分方程程序記為P。

2) 實例化一階非線性常微分方程y′=f(x,y),簡化后的方程為一階線性常微分方程,記為y′=a*y(a為實數或復數)。方程y′=a*y對應的Runge-Kuta法記為Runge-Kuta1,對應的實現Runge-Kuta1法解一階線性常微分方程的程序記為P’。

3) 對一階線性常微分方程y′=a*y構造蛻變關系MRi(i=1,2,3…),用MRi驗證實例化的程序P’,若程序P’存在錯誤,則可推斷原始程序P中存在錯誤。

4 一階非線性常微分方程蛻變測試實例

4.1 實例化一階非線性常微分方程

對于一個解一階非線性微分方程y′=f(x,y)的程序P,直接檢測出其中是否存在錯誤是有一定難度的。若能在其對應的解實例化后的一階線性微分方程y′=g(x,y)的程序P′中檢測出變異的存在,則能證明原始程序P的算法是有錯誤的。

因此,將原始的非線性函數f(x,y)=-x*y2實例化為一個線性函數g(x,y)=u*y,作為程序的初始函數。令u=-3,此時實例化后的新微分方程記為一階線性微分方程(4)

(4)

同樣在程序中植入變異Mutant1,將上述實例化后的解一階線性微分方程的原始和植入錯誤的程序編譯執行后,得到的運行結果趨勢如圖5所示。

圖4 線性原始和變異運行結果圖

遺憾的是,從以上兩個程序運行結果中依舊只能發現與圖2即最初的常微分方程程序運行結果類似的規律,即隨著x值的逐步增大,y值依舊在逐漸遞減,且最終的y100值在變異后程序中的運行結果與原始程序的運行結果均近似為0(由于程序中數值精度有限,計算結果存在一定的誤差)。進而說明,通過將微分方程實例化到一個相對簡單的一階線性常微分方程上,是不足以驗證原始的解一階非線性微分方程程序是否存在錯誤的。

4.2 解一階線性微分方程程序的蛻變測試方法

4.2.1 蛻變關系的構造

通過對一階線性微分方程(4)構造蛻變關系來驗證一階線性常微分方程程序的正確性,進而分析原始程序是否存在錯誤。一階線性常微分方程(4)可表達為

(5)

解方程(5)的程序記為被測程序P′。根據一階線性微分方程的一般數值求解方法,可得出式(5)的通解為

y=e3*e-3x,c=e3

(6)

根據式(6)的性質,可以構造出以下蛻變關系,如圖5所示。

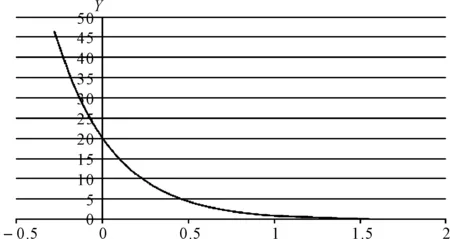
圖5 y=e3*e-3x函數圖像

在上圖中可以看出隨著x值的逐漸增大,y值是單調遞減的,且y值始終大于0。根據這一條性質,可以構造蛻變關系1,記為MR1。則MR1可描述為

MR1：?i,j∈且iy(xj)>0。

當x取它的相反數-x時,此時對應的函數為y=e3*e3x,函數y與y’關于y軸對稱,且存在恒等式y(xk)*y(-xk)=e6。根據這一條性質,可以構造出蛻變關系2,記為MR2。則MR2可描述為

MR2：?k∈,y(xk)*y(-xk)=e6。

以上兩條蛻變關系MR1,MR2就是測試執行被測程序P’的所用到的蛻變關系。若程序執行結果未滿足以上的關系,就有充分的理由斷定被測程序P’存在錯誤。

4.2.2 測試結果

根據MR1和MR2在Windows環境下使用VC++編譯器執行變異程序,選取程序的部分運行結果如表1所示。其中最后一列的yx*y-x為由蛻變關系MR2構造的衍生測試用例。

從表1中可以看出,對于任意逐漸增大的x值,y值始終在不斷遞減且y>0。因此蛻變關系MR1檢測不到程序的任何錯誤。而在最后一列yx*y-x中,yx*y-x的值很明顯不等于e6,因此利用蛻變關系MR2,檢測出了解一階線性常微分方程的程序存在異常,即蛻變關系MR2的檢錯能力大大高于蛻變關系MR1。這是由于MR2的輸入變換約束力更強,較MR1更為復雜,與“優先考慮輸入的蛻變關系表達式較復雜一方”的原則一致[9]。實驗證明原始的解一階非線性常微分方程的程序存在異常,程序版本Mutant1存在缺陷。

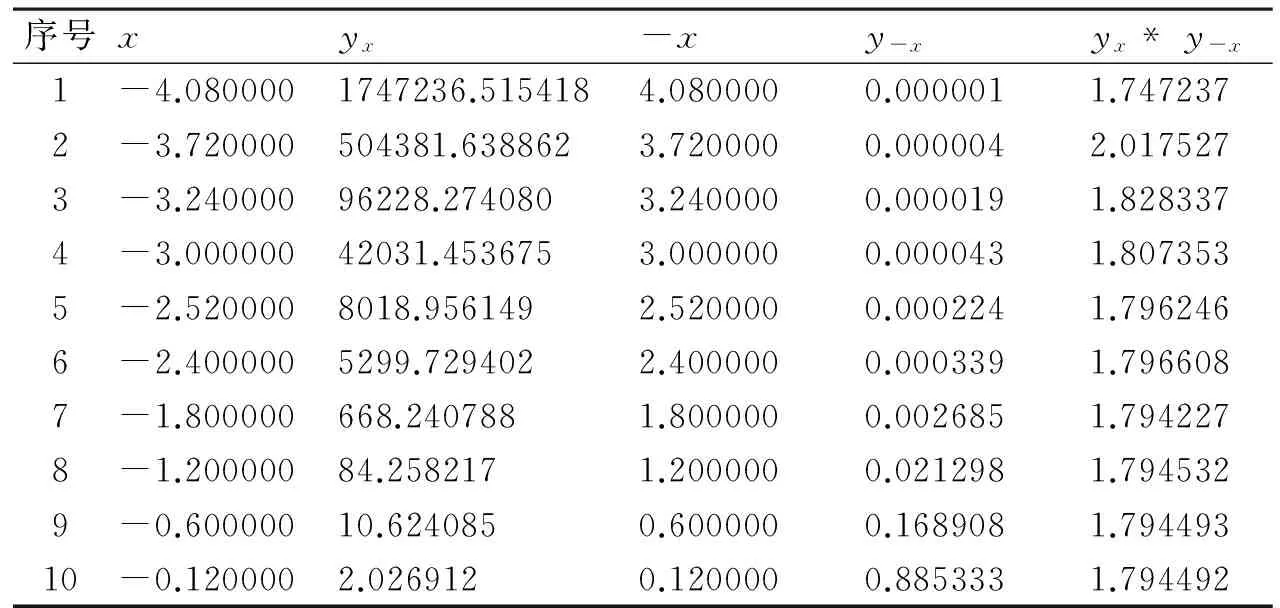
表1 測試執行結果

5 結語

因為缺少分析方法,大多數微分方程通常通過數值方法解決。由于如前面章節所說的種種原因,對于這樣的數值方法可能不存在測試Oracle。而將微分方程簡化并聚焦到一階線性常微分方程問題上,會有助于解決一些問題,但是還不足以暴露出一些細微的錯誤,比如本文中所描述的錯誤。相反的,我們在簡化的方程的基礎上確定了蛻變關系并進行了蛻變測試,然后設法從程序中找出問題所在。

本文以一階線性常微分方程為例,總結了蛻變測試是如何幫助減少數值計算軟件測試中的Oracle問題,并通過實驗證明利用蛻變關系的構造可以檢測出微分方程程序中的一些細微問題,在未來的更深入的微分方程的應用中我們可以得到進一步的鉆研。

[1] Chen T Y,Cheung S C,Yiu S M.Metamorphi-c testing：A new approach for generating next test cases[R].HKUST-CS98-01.Hong Kong,1998.

[2] Chen T Y,Huang D H,Tse T H,et al.Case studies on the selection of useful relations in metamorphic testing[C]// Symposium on Software Engineering&Knowledge Engineering.Madrid,Spain,2004：569-583.

[3] Chen T,Feng T H,Tse.Metamorphic testing of programs on partial differential equations：a case study[C]// Proceedings of the 26th Annual International Computer Software and Applications Conference. Baltimore,Marriott,USA,2002：327-333.

[4] 姚奕,黃松,稽孟雨.面向整數錯誤檢測的蛻變測試方法研究[J].計算機工程與科學,2012：52-56.

[5] 李榮華,劉博.微分方程數值解法[M].第四版.北京：高等教育出版社,2009：38-41.

[6] Khodabin M,Rostami M.Mean square numerical solution of stochastic differential equations by fourth order Runge-Kutta method and its application in the electric circuits with noise[J]. Advances in Difference Equations,2015：3-19.

[7] Chapra S C and Canale R P.Numerical Methods for Engineers：with Software and Programming Applications[M].New York：McGraw-Hill,2002.

[8] Offutt A J,Rothermel G,Zapf C.An experime-ntal evaluation of selective mutation[C]// Proceedings of the Fifteenth International Conference on Software Engineering.IEEE Computer Society,Washington DC,2003：100-107.

[9] Dong G W,Nie C H,Xu B W,et al.An effective iterative metamorphic testing algorithm based on program path analysis[C]//Proceedings of the 7th Annual International Conference on Quality Software.IEEE Computer Society,Washington DC,2007：292-297.

[10] WU Peng,SHI Xiao-Chun,TANG Jiang-Jun,et al.Metamorphic Testing and Special Case Testing:A Case Study[J]. Journal of Software,2005：1210-1214.

[11] Manolache L I,Kourie D G.Software Testing Using Model Programs[J].Software Practice and Experience,2001,31(13)：1211-1236.

版 權 聲 明

本刊已許可萬方數據庫、中國學術期刊(光盤版)電子雜志社在中國知網及其系列數據庫等產品中以數字化方式復制、匯編、發行、信息網絡傳播本刊全文。著作權使用費與本刊稿酬一并支付。作者向本刊提交文章發表的行為即視為同意我編輯部上述聲明。

《艦船電子工程》編輯部

Metamorphic Testing of Ordinary Differential Equations Program

QIU Shuting ZHANG Zhixiang

Numerical methods are widely used in our real life, solving differential equations is an important branch of numerical problems. But it is difficult to find a test Oracle to verify the effectiveness of programs which solving differential equations. In this paper, metamorphic testing method is used to detect the effectiveness of the program which used to solve differential equations. Through analyzing the case of a typical program case, we propose the metamorphic test method of solving ordinary differential equations. At last, an instance is verified to illustrate the validity of this method.

numerical calculation, differential equations, metamorphic testing, Oracle problem

2016年6月9日,

2016年7月25日

邱舒婷,女,碩士研究生,研究方向:軟件質量保證技術。張志祥,男,副教授,碩士生導師,研究方向:程序設計方法,軟件工程等。

TP311

10.3969/j.issn.1672-9730.2016.12.007