高速鐵路平面曲線特征點偏移接受域研究

朱洪濤，劉敏，魏暉，龍輝

(1．南昌大學機電工程學院，江西南昌330031;2．江西科技學院汽車工程學院，江西南昌330098)

高速鐵路平面曲線特征點偏移接受域研究

朱洪濤1，劉敏1，魏暉2，龍輝1

(1．南昌大學機電工程學院，江西南昌330031;2．江西科技學院汽車工程學院，江西南昌330098)

以高速鐵路曲線整正作業時的正矢作為研究對象，通過分析實測正矢偏差的組成，建立了一種優化線形與設計線形間的正矢偏差模型，并以軌道實測正矢平順性判定結果不變(不超限)為條件，提出了一種平面曲線特征點偏移接受域(即所允許的特征點最大偏移量)算法。該算法為評價特征點辨識精度是否合適以及判斷線路的變形是否會對整體平順性的判定結果造成影響，進而決定是否以優化線形代替設計線形對實測線路進行整正作業提供了理論依據。該算法可以移植應用到普速、快速線路中。

高速鐵路;平面曲線;軌道平順性;特征點;優化線形;接受域

既有線在運營過程中，受列車的動載和自然環境等因素的作用，軌道的幾何狀態會不可避免地產生變形或錯動，形成軌道不平順［1-2］。軌道不平順是輪軌系統的激擾源，對行車的安全性、平穩性、舒適性以及軌道和機車的零部件使用壽命都會產生重大的影響，尤其是在薄弱的曲線位置影響更大［3］。因此，需要對軌道平順性進行定期檢查，必要時進行線路整正，恢復軌道的平順性［4］。目前線路整正方法主要是以實測值與設計值之間的偏差為依據［5］，然而當軌道實際位置相較于設計位置發生較大偏移時，尤其是當某些路段發生方向一致的整體性偏移時，現有的整正法并不是最經濟、總體調整量最小的方案［6］。合理的整正方法是根據實測數據對軌道進行特征點等參數的辨識，構造實測曲線的優化線形(由標準的緩和曲線和圓曲線組成的標準線形)，進而指導整正作業［7］。

對于特征點的辨識，文獻［8-10］分別介紹了基于絕對測量數據相鄰弦方位角變化、平面曲線定長弦斜率變化以及基于超高的最小二乘擬合來對曲線特征點進行辨識，但是，對于辨識精度是否合適均沒有給出明確的評價方法。此外，由于各線路處在不同的動載和自然環境下，線路的變形程度各不相同，若對所有變形線路都通過辨識特征點等參數來構造優化線形進而指導整正作業，不僅耗時耗力而且并非最合適的選擇。為了充分利用天窗期保證軌道的高平順性，尋找一種判別線路的變形是否會對整體平順性的判定結果造成影響，進而決定是否以優化線形代替設計線形指導整正作業的理論依據具有實際意義。

軌道不平順涉及參數眾多，正矢具有代表性，因此選擇正矢作為研究對象，以實測正矢平順性判定不變(不超限)為條件，提出了平面曲線特征點偏移接受域算法。該算法通過將實測線路的特征點辨識誤差與特征點偏移接受域進行比較，判斷特征點辨識精度是否合適，通過比較實測線路特征點辨識位置與設計位置的偏差量是否超過特征點偏移接受域來判斷線路的變形是否對軌道整體平順性的判定結果造成影響，從而決定是否以優化線形對實測線路進行整道。

1 特征點偏移接受域求解原理

以基于0級軌道檢查儀的相對測量為例分析其軌道檢查過程可知，正矢平順性的判定是基于實測值與設計值之間的偏差。然而由于受線路變形與軌檢儀儀器誤差的影響，實測正矢相對于設計值的偏差主要由3方面組成:優化線形相對于實際線形的正矢偏差值、軌檢儀正矢項的儀器誤差以及優化線形相對于原設計線形的正矢偏差。上述情況可用數學模型表示為

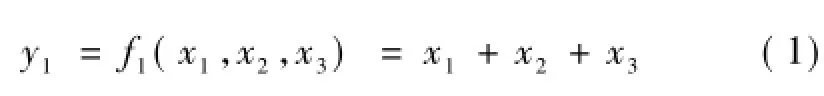
式中:y1為實測正矢偏差值;x1為軌檢儀正矢項的儀器誤差;x2，x3分別為優化線形相對于原設計線形和實際線形的正矢偏差。

經分析可知，x1與x2是實測正矢偏差的主要誤差來源，二者的合成誤差y2表示為

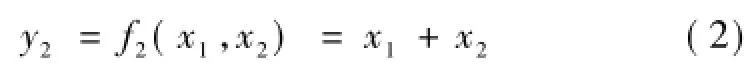
根據微小誤差舍棄原則［11］，當測量過程中的誤差數值不大于總誤差的1/3時，對測量的最終結果基本不會產生影響。這種誤差稱為微小誤差，在計算測量結果總誤差時可以不予考慮。根據文獻［12］，250～350 km/h線路曲線正矢容許偏差管理值為2～5 mm。從嚴選擇2 mm作為正矢偏差限值，根據上述原則可知，測量過程中當合成誤差y2的大小不超過測量允許的微小誤差值(0.667 mm)時，不會引起實測正矢超差。

在軌道整體實測正矢平順性判定結果不變(不超限)的情況下，根據合成誤差y2、儀器誤差(根據文獻［13］要求按A類不確定度［11］評定方法求得)以及正矢偏差限值的微小誤差值，求解優化線形相較于設計線形的正矢偏差，再根據優化線形與設計線形之間的偏差模型，求解特征點偏移接受域。求解原理見圖1。

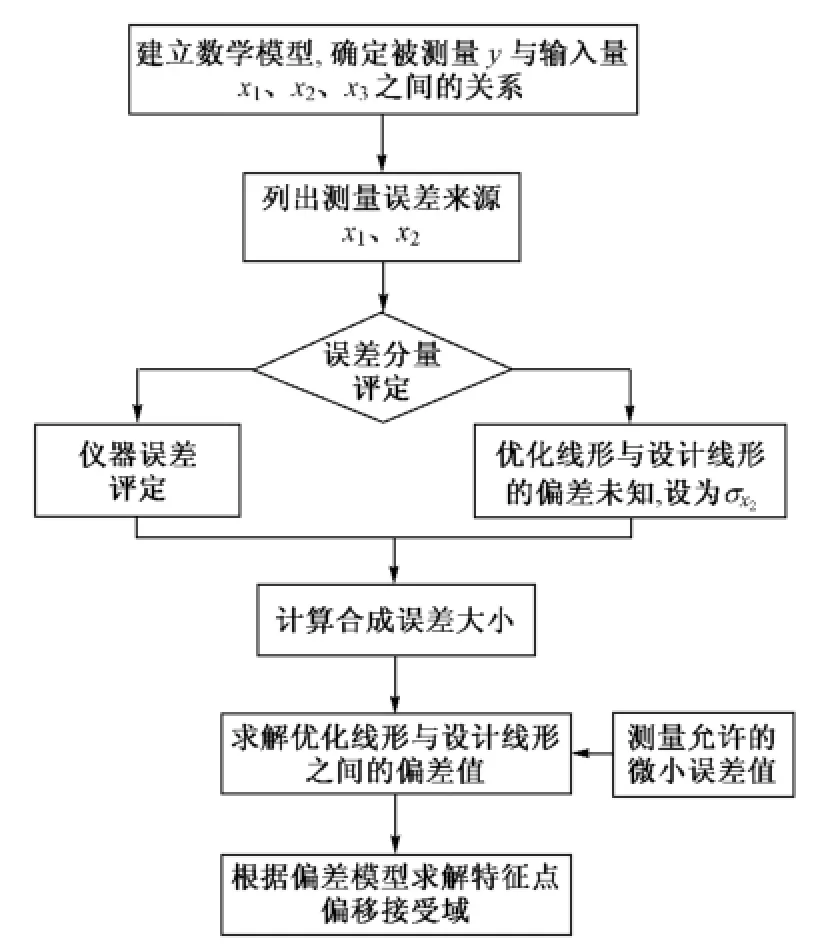
圖1 特征點偏移接受域求解原理

2 軌檢儀儀器誤差的確定

由于高速鐵路對軌道平順性的要求較高，在計算特征點偏移接受域時應考慮軌檢儀儀器誤差。

根據文獻［13］的規定，通常選擇測量重復性條件下的標準差來表征軌道檢查儀的儀器誤差。由標準不確定度的B類評定方法［11］可知，0級軌檢儀的儀器誤差為0.375 mm，但B類評定法并不能真實反映某類0級軌檢儀的儀器誤差，可能會大于某類0級軌檢儀的真實儀器誤差。為此，選擇標準不確定度的A類評定方法對儀器誤差進行評定。具體的試驗要求如下:采用軌檢儀對滿足試驗要求的軌道進行5次往返測量，在試驗有效區間隨機選取50個實測點，作每次實測正矢的測量值與該點10次實測正矢平均值之差，求其絕對值，按由小到大排列，根據95%的置信概率確定儀器誤差(標準差)。

根據上述試驗要求，選取了6臺帶長波功能的GJY-T-EBJ-3型0級軌道檢查儀對符合上述試驗要求的軌道線路進行試驗，得到6組儀器誤差，見表1。

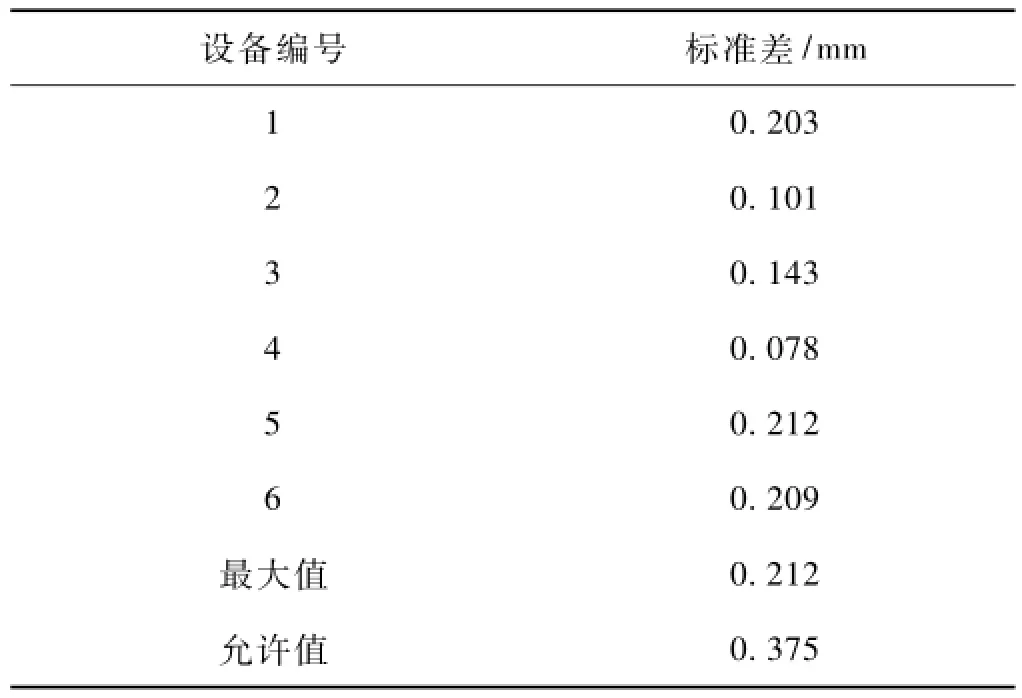
表1 0級軌檢儀儀器誤差

選擇其中的最大值0.212 mm作為所選取的這種0級軌檢儀的儀器誤差，其測量重復性如圖2所示。其中實測1-1、實測1-2代表第1次測量的正反行程，其余類推。

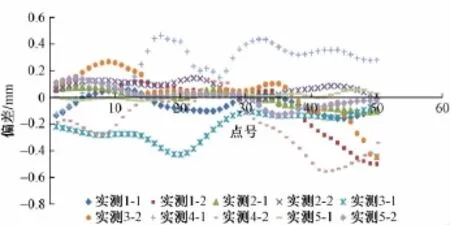
圖2 0級軌檢儀測量重復性

3 優化線形與設計線形的正矢偏差模型

由于不同線路的設計參數各不相同，實測線路的優化線形與其設計線形之間的偏差也各不相同。為便于在實測作業中快速知道特征點的偏移接受域，需建立起統一的優化線形與設計線形之間的偏差模型，通過導入不同線路的設計參數，可方便求解出不同線路的特征點偏移接受域。

3.1 曲線軌道設計正矢

考慮到設計線形和優化線形均具有前后對稱性，以前緩和曲線與圓曲線的前半段為例，計算曲線軌道的設計正矢。根據文獻［4］可知，半徑為R，弧長為L的圓曲線上各點(起點和終點除外)正矢fc計算式為

常用緩和曲線各測點(測點間隔為10 m)正矢為

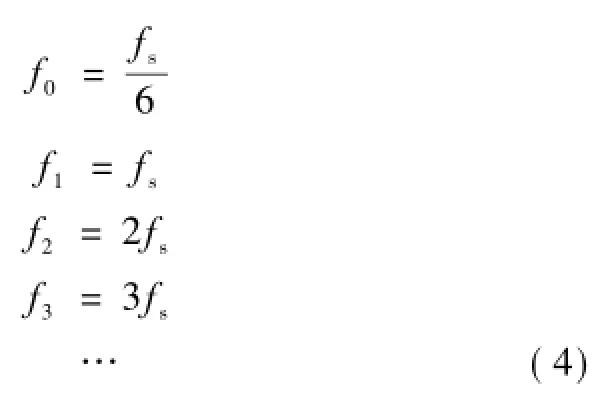
式中:fi為緩和曲線各測點的正矢，i=0～n;fs為緩和曲線的正矢遞增率，當緩和曲線的分段數為n時，有

緩圓點PHY正矢大小一般為fc－f0，據此可以建立起任意曲線軌道的設計線形模型。

3.2 正矢偏差模型

依據上述特征點偏移接受域求解原理，需建立軌道優化線形相對于原始設計線形的偏差模型，見圖3。實測線形特征點相對于設計線形特征點的偏移方向與偏移量大小各不相同，由此造成優化線形與設計線形之間的偏差量也各不相同。考慮極端情況，假設直緩點與緩圓點均偏向同一側且都同時為不引起實測正矢平順性判定改變的最大偏移量，則此時實測線路優化線形與設計線形之間的偏差為最大。

圖3 優化線形與設計線形偏差模型

由圖3可知，當滿足上述假設的偏移情況時，優化線形與設計線形之間的最大偏差出現在緩和曲線線性部分，其偏差量可以用線性公式計算。

根據上述條件，設計線形與優化線形的前緩和曲線線性段的斜率k為

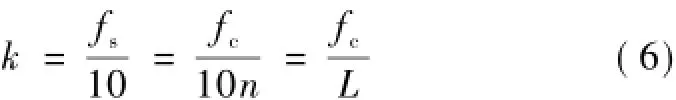
由此可求得線性段直線方程分別為

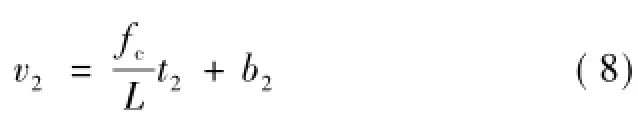
式中:v1，v2分別為設計線形和優化線形的計劃正矢，t1，t2分別為v1，v2對應里程;b1，b2分別為對應直線的截距。

正矢平順性判定結果不變情況下優化線形與設計線形之間的正矢最大偏差值(標準差)σx2為

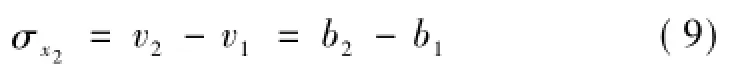
4 特征點偏移接受域算法

根據文獻［11］可知x1，x2為隨機誤差，相互獨立，由函數的隨機誤差的計算原理可得

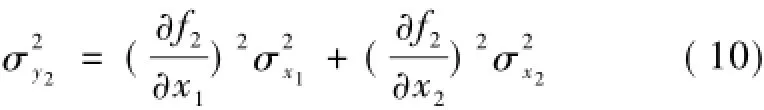
式中:σy2為y2的標準差;σx1為軌檢儀儀器誤差(標準差);為誤差傳遞系數。

根據微小誤差舍棄準則當總附加誤差y2小到一定程度時，其對測量結果y1(標準差為σy1)的影響較小，計算測量結果時可以不考慮。具體舍棄條件為

因正矢偏差限值為2 mm，則σy1=2 mm，由此得

由式(2)、式(10)、式(12)得

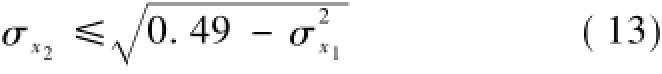
通過優化線形與設計線形之間的偏差模型，可以快速求解出軌道正矢平順性判定結果不發生變化時所允許的特征點最大偏移量。σx1=0.212 mm，代入式(13)得σx2=0.667 mm。

根據優化線形與設計線形的正矢偏差模型，可以計算出設計線形與優化線形的緩圓點里程坐標(其余特征點計算類似)為

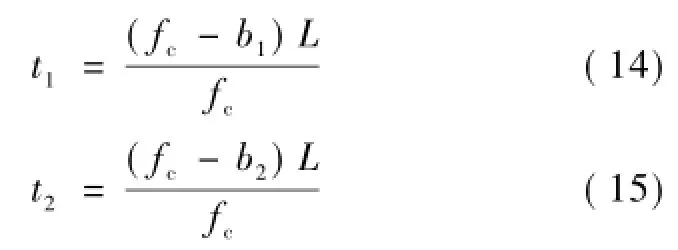
優化線形緩圓點與設計線形緩圓點之間的最大偏移量為

5 算例

不同線路有著不同的緩和曲線長度以及圓曲線半徑值，為了從整體上表示緩和曲線長度、曲線半徑和特征點偏移接受域三者之間的關系，選擇了文獻［14］中關于緩和曲線長度和曲線半徑的配對值，根據求解特征點偏移接受域的算法，通過MATLAB計算出特征點偏移接受域。三者之間的關系見圖4。

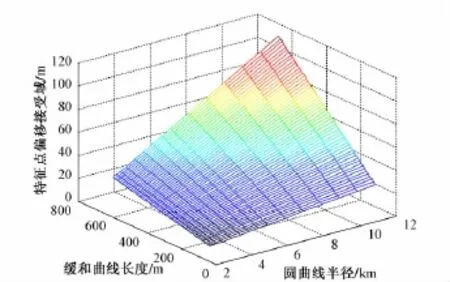
圖4 特征點偏移接受域、緩和曲線長度和圓曲線半徑三者之間的關系

由圖4可知，圓曲線半徑越大、緩和曲線越長時，特征點偏移接受域也越大。不同設計行車速度的高鐵線路對最小曲線半徑有限制，同時設計行車速度與曲線半徑一定時對緩和曲線長度也有最小值限制。將上述同一設計行車速度下的最小曲線半徑和最小緩和曲線長度作為困難情況取值。了解困難情況下特征點偏移接受域，可以將此作為同一設計行車速度線路中評價特征點辨識精度是否合適以及判斷線路變形是否會對整體平順性判定造成影響的最嚴格判別標準。困難情況下特征點偏移接受域見表2。同一設計行車速度下的任何線路，若其辨識誤差小于特征點偏移接受域，有95%的置信概率認為特征點的辨識誤差不會對軌道平順性的判定造成影響。特征點辨識位置與設計位置之差的絕對值只要小于困難情況下特征點偏移接受域，就可以從正矢平順性判定不變的角度認為該線路仍可按照設計線形進行整道，線路的變形不會對整體平順性產生影響。對于不滿足困難情況下特征點偏移接受域的線路，可根據本文算法作進一步計算，通過特征點辨識位置與設計位置之差的絕對值是否超過該線路特征點偏移接受域，從而對線路的變形是否會對整體平順性判定產生影響以及是否需要以優化線形代替設計線形指導整道作業作出判斷。

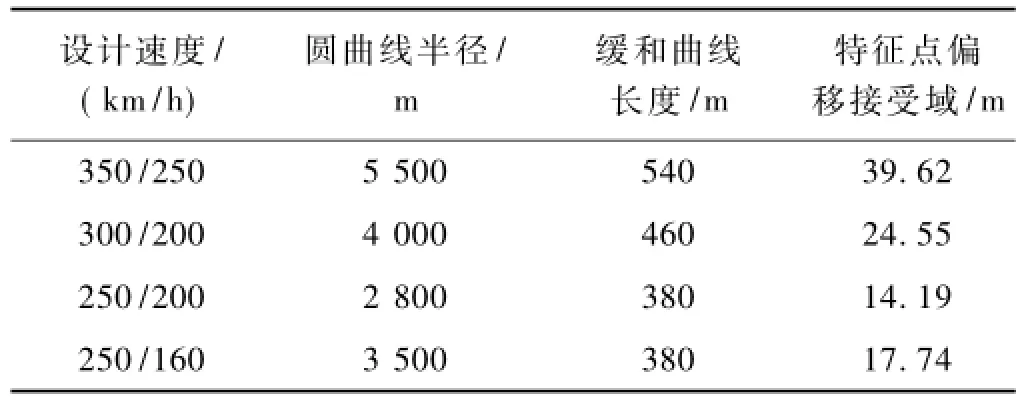
表2 困難情況下特征點偏移接受域

6 結論

1)分析了實測正矢偏差的組成，建立了一種優化線形與設計線形之間的正矢偏差模型，并以此為依據，以軌道實測正矢平順性判定結果不變(不超限)為條件，提出了一種平面曲線特征點偏移接受域算法。

2)將特征點辨識誤差與特征點偏移接受域進行比較，若其辨識誤差小于特征點偏移接受域，有95%的置信概率認為特征點的辨識誤差不會對軌道平順性的判定造成影響。

3)比較實測線路特征點辨識位置與特征點設計位置的偏差量是否超過特征點偏移接受域，判斷是否以優化線形代替設計線形對實測線路進行整道。若不超過，則有95%的置信概率認為線路的變形不會對軌道平順性的判定造成影響，仍可按設計線形整道。

本文特征點偏移接受域算法具有可移植性，亦可應用于普速、快速線路中。

［1］EASA S M．Practical Optimization Model for Realigning Railway Horizontal Curves［J］．Civil Engineering and Environmental Systems，1991，8(1):27-36．

［2］任軼南．基于現代檢測技術的高速鐵路曲線狀態評價與整正方法［D］．成都:西南交通大學，2015．

［3］羅林，張格明，吳旺青．輪軌系統軌道平順狀態的控制［M］．北京:中國鐵道出版社，2006．

［4］郝瀛．鐵道工程［M］．北京:中國鐵道出版社，2000．

［5］賈金民，馬彥濤，關學生．淺議用坐標法計算既有線曲線［J］．鐵道建筑，2010(2):102-105．

［6］宋韜．鐵路既有線整正優化相關算法研究［D］．成都:西南交通大學，2014．

［7］陳峰．提速線路精密測量、重構與優化整正研究［D］．長沙:中南大學，2013．

［8］郭良浩，劉成龍，宋韜，等．鐵路既有線平面和豎面線形精確分段方法研究［J］．鐵道工程學報，2014，31(7):48-52．

［9］張強，劉成龍．鐵路既有線復測平面曲線分區新方法［J］．測繪工程，2014，23(8):58-61．

［10］陳峰．鐵路既有線復測平面曲線優化方法［J］．鐵道科學與工程學報，2012，9(5):90-95．

［11］費業泰．誤差理論與數據處理［M］．北京:機械工業出版社，2004．

［12］中華人民共和國鐵道部．TG/GW115—2012高速鐵路無砟軌道線路維修規則(試行)［S］．北京:中國鐵道出版社，2012．

［13］中華人民共和國鐵道部．TB/T 3147—2012鐵路軌道檢查儀［S］．北京:中國鐵道出版社，2012．

［14］中華人民共和國鐵道部．TB/T 10621—2009高速鐵路設計規范(試行)［S］．北京:中國鐵道出版社，2009．

Research on Acceptable Region for Plane Curve Feature Points Deviation on High Speed Railway

ZHU Hongtao1，LIU Min1，WEI Hui2，LONG Hui1
(1．School of Mechanical＆Electrical Engineering，Nanchang University，Nanchang Jiangxi 330031，China; 2．School of Automotive Engineering，Jiangxi University of Technology，Nanchang Jiangxi 330098，China)

T aking the versine of high speed railway curve adjustment operation as the research object，a versine deviation model between optimal alignment and design alignment was established by analyzing the constitution of measured versine deviation．A new algorithm for plane curve feature point offset acceptance region，which was the allowed maximum offset of the feature point，was proposed in the condition of invariant judgment result(no exceeding)for the measured track versine regularity．T his algorithm provides a theoretical basis for evaluating the suitability for feature point identification accuracy and the influence of the track distortion on judgment result of the whole track regularity for deciding to whether implement the adjustment for actual railway track by replacing design alignment with optimal alignment or not，which could be applied to the normal speed railways and fast railways．

High speed railway;Plane curve;T rack regularity;Feature point;Optimal alignment;Acceptance region

U216.3

A

10．3969/j．issn．1003-1995．2016．12．22

1003-1995(2016)12-0082-05

(責任審編李付軍)

2016-04-18;

2016-07-20

國家自然科學基金(51468042);江西省自然科學基金(20142BAB206003);江西省重點研發計劃(20161BBE50079)

朱洪濤(1962—)，男，教授，碩士。