勁性骨架拱橋施工階段應力不確定性及敏感性分析

張正陽，趙人達

(西南交通大學橋梁工程系，四川成都610031)

勁性骨架拱橋施工階段應力不確定性及敏感性分析

張正陽，趙人達

(西南交通大學橋梁工程系，四川成都610031)

勁性骨架拱橋應力受各種隨機因素的影響在施工期間就表現出較強的不確定性，確定性分析已不能滿足計算精度的要求。本文通過北盤江大橋模型試驗，研究勁性骨架拱橋施工期間應力的不確定性及敏感性，結合貝葉斯方法引入早期應力觀測數據對不確定性分析結果進行修正，得到結構應力后驗概率分布。研究結果表明:結構應力在施工前期離散性較小，后期逐漸變大;經過貝葉斯修正的結構應力后驗概率分布離散性得到明顯改善;各變量敏感系數在施工期間均有不同程度的波動，徐變模型敏感系數最大，收縮模型敏感系數在施工前期較大，后期較小。

勁性骨架拱橋;不確定性;敏感性;貝葉斯理論;模型試驗

勁性骨架既作為施工中的支架，主要承受后期澆筑混凝土的重量及各種施工荷載，施工結束后又作為結構的永久組成部分與外包鋼筋混凝土共同受力。拱橋采用自重輕、剛度大、易架設的鋼管混凝土為勁性骨架，極大地降低了施工難度，增加了混凝土拱橋的跨徑，使勁性骨架拱橋迅速成為大跨徑混凝土拱橋最有競爭力的橋型［1］。目前世界上跨度最大的鋼筋混凝土拱橋萬縣長江大橋(主跨420 m)和滬昆鐵路北盤江大橋(主跨445 m)均采用此種橋型。

勁性骨架拱橋一般跨度較大，且外包混凝土各組分之間有較大齡期差，施工期間荷載和截面特性不斷變化，導致收縮徐變的影響十分復雜。我國對于勁性骨架拱橋收縮徐變的研究開始于毛瑞祥等［2］對宜賓小南門金沙江大橋的收縮徐變效應的分析。劉忠等［3］基于萬縣長江大橋模型試驗，對萬縣長江大橋的收縮徐變效應進行了研究;謝肖禮等［4］推導出了考慮混凝土彈性后效及四周約束作用的鋼管混凝土截面應力重分布表達式。

勁性骨架拱橋外包混凝土的施工特點導致了施工期間收縮徐變的影響不容忽視，而目前的研究大多集中于運營階段，對施工階段的研究稍顯不足。本文依靠滬昆鐵路北盤江大橋模型試驗，對鋼管混凝土勁性骨架拱橋施工期間混凝土應力進行了不確定性分析。同時采用貝葉斯方法引入短期觀測數據對混凝土應力先驗概率分布進行修正，得到混凝土應力的后驗概率分布特性。最后采用敏感性分析方法分析了結構應力對各隨機變量的敏感程度。

1 北盤江大橋模型試驗概況

北盤江大橋主跨445 m，矢高100 m，鋼管直徑750 mm，為了保證模擬效果，同時考慮模型構件的生產制作難度，決定采用1∶7.5的相似比例制作拱肋模型。模型橋跨度59.333 m，設置預拱度后矢高13.413 m，拱肋模型的截面尺寸如圖1所示。

圖1 模型橋拱肋截面尺寸(單位:mm)

縮尺后構件的尺寸比較小，例如模型橋鋼管內徑為94 mm，而實橋管內C80混凝土骨料直徑為5～20 mm，如果采用實橋材料會影響其流動性甚至發生堵管現象。為了保障施工的可行性對模型材料做了部分調整，如表1所示。

表1 模型橋與實橋材料對比

模型橋的施工包括鋼管骨架的架設、內填混凝土的灌注、外包混凝土的澆筑以及各部分配重的加載。外包混凝土縱向分為3段，即全包段1、全包段2和分包段。分包段各組分的施工順序為邊箱底板→腹板→邊箱頂板→中箱底板→中箱頂板。利用Midas有限元分析程序建立空間梁單元模型對模型橋受力進行模擬，鋼管與混凝土之間采用剛性連接模擬2種材料的共同作用。根據實際的情況將施工過程從鋼骨架合龍到澆筑中箱頂板分為24個工況，見表2。其中關鍵工況為第5工況澆筑邊箱底板、第15工況腹板配重、第24工況澆筑中箱頂板。

表2 模型試驗工況

2 分析模型及方法

收縮徐變模型采用《公路橋涵鋼筋混凝土和預應力混凝土結構設計規范》(JTG D62—2004)中采用的CEB-FIP(1990)模型。分別采用α1，α2，α3，α4表示徐變模型、收縮模型、混凝土強度和環境相對濕度不確定性因子，則結構應變的不確定計算模型可以表述為如下形式

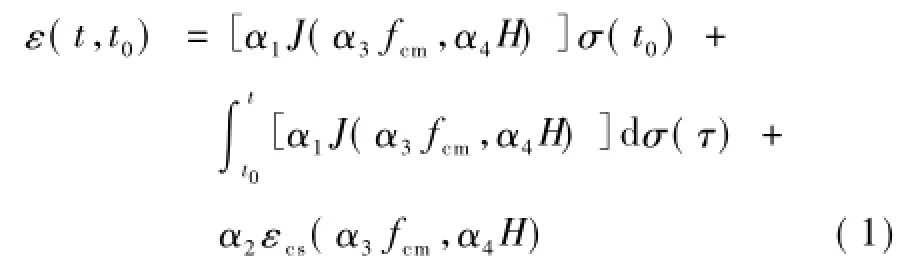
式中:ε(t，t0)為加載時刻t0到計算時刻t的總應變; J為徐變函數;fcm為混凝土強度;H為環境相對濕度;σ為應力;εcs為收縮應變。

對于CEB-FIP(1990)模型，α1，α2，α3，α4服從均值為1的正態分布，變異系數分別取0.35，0.46，0.15，0.2［5］。

分別對α1，α2，α3，α4進行2n次拉丁超立方抽樣［6］，結合變量均值構成2n+1組樣本，代入有限元程序計算可得到結構響應yi(i=1，2，…2n+1)。根據以上樣本值及結構響應值可以構造結構響應和變量間的顯示函數，如下式所示

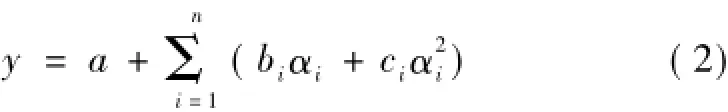
式中，a，bi和ci為函數的2n+1個待定系數，將2n+1組抽樣值及結構響應值代入解2n+1個方程來確定。本文定義敏感系數ρi如下

式中，σ(αi)為隨機變量因子αi的均方差。

引入均方差的意義在于考慮變量離散性對變量敏感度的影響，隨機變量因子以其均值代入計算。

3 不確定性及敏感性分析結果

本文采用拉丁超立方抽樣法得到了1/4跨和跨中邊箱底板混凝土應力的先驗分布，如圖2所示。圖中應力為負表示受壓，μ表示預測均值，σ為預測值標準差。由圖2可以看出混凝土應力的離散性隨著施工的進行而不斷增加，第15工況前離散性較小，第15工況后離散性增加明顯。產生這種情況的原因是因為各隨機變量的不確定性隨時間的增加而增加，且隨著施工的進行，自然或人為等更多不確定性因素也會不斷加入。第24工況1/4跨混凝土應力預測區間為［－18.88，－12.06］(MPa)，試驗值為－16.62 MPa;跨中混凝土應力預測區間為［－17.90，－11.35］(MPa)，試驗值為－15.66 MPa。

圖2 應力先驗分布

先驗分布總體預測結果良好。但是后期預測結果離散性較大。這種情況可以通過貝葉斯方法［7］進行改善，如圖3所示。從圖3可以看出，經過貝葉斯修正后的后驗預測結果離散性較先驗預測結果小很多。第24工況，1/4跨混凝土應力后驗預測區間為［－17.78，－15.37］(MPa)，跨中混凝土應力后驗預測區間為［－16.87，－14.22］(MPa)。相比先驗預測區間，后驗預測區間大為減小，可以減小設計中不必要的浪費，提高施工過程中應力調整措施的精度。

根據敏感性分析方法，分別計算了施工階段1/4跨和中跨邊箱底板混凝土應力對于各個隨機變量的敏感性，如圖4所示。從圖4可以看出，敏感系數最高的變量為徐變模型的不確定性，選擇合理的徐變模型是控制混凝土應力預測精度最有效的措施。各個變量的敏感系數在施工階段有較大起伏，同一個變量在不同的工況對混凝土應力的影響程度不同。收縮模型的不確定性在前期敏感系數較高，后期敏感系數相對較小。混凝土強度的敏感系數最小，而且最為穩定，說明它對混凝土應力的影響程度最小。

圖3 應力后驗分布

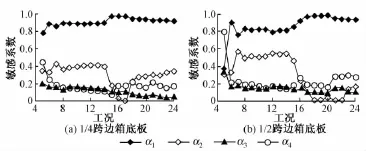
圖4 底板應力敏感系數

4 結語

勁性骨架拱橋由于其跨度大、施工周期長、施工方法復雜等，使得施工階段受到收縮徐變影響已較為顯著，應力分布的離散特性隨著施工的進行而不斷加大。通過貝葉斯方法修正先驗預測得到后驗預測結果可以明顯改善這種離散性。北盤江大橋模型試驗結果驗證了此方法的正確性，預測結果與試驗結果吻合良好且精度較高。通過敏感性分析得到徐變模型不確定性對應力預測結果的離散性影響較為顯著，在實際工作中應盡量選用離散性較小的徐變模型，從而得到更為精確的預測結果。

［1］陳寶春，葉琳．我國混凝土拱橋現狀調查與發展方向分析［J］．中外公路，2008，28(2):89-96．

［2］毛瑞祥，徐岳，張人范，等．徐變收縮對勁性鋼骨混凝土拱肋影響的計算方法［J］．中國公路學報，1991，4(4):37-44．

［3］劉忠，顧安邦，周水興．萬縣長江大橋非線性綜合分析［J］．重慶交通學院學報，1996，15(增):19-29．

［4］謝肖禮，秦榮，彭立文，等．鋼管混凝土勁性骨架拱橋收縮徐變影響理論研究［J］．中國工程科學，2001，3(3):80-84．

［5］徐騰飛，向天宇，趙人達，等．預應力混凝土梁長期變形的隨機分析［J］．土木建筑與環境工程，2013，35(1):113．

［6］MCKAY M D，CONOVER W J，BECKMAN R J．A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code［J］．Technometrics，1979，21(2):239-245．

［7］BAZANT Z P，KIM J K．Segmental Box Girder:Deflection Probability and Bayesian Updating［J］．Journal of Structure Engineering，1989，115(10):2528-2547．

Analysis of Stress Uncertainty and Sensitivity of Stiffened Skeleton Arch Bridge During Construction Stage

ZHANG Zhengyang，ZHAO Renda
(Department of Bridge Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China)

Stress of stiffened skeleton arch bridge is uncertain，because it's influenced by many random factors during construction stage，certainty analysis cannot satisfy the calculation accuracy．Based on the model test of Beipan river bridge，the stress uncertainty and sensitivity of stiffened skeleton arch bridge during construction stage were studied in this paper．Bayesian theory was introduced into the prior stress observation data，the posterior probability distribution of stress was obtained by modifying the results of uncertainty analysis．T he results show that the discreteness of stress is small in the early construction stage and become large later．T he discreteness of the posterior probability distribution of stress is improved by Bayesian modification．T he sensitivity coefficient of variables fluctuate during construction stage，such as the sensitivity coefficient of creep model is the largest，the sensitivity coefficient of the shrinkage model is large at first and become small later．

Stiffened skeleton arch bridge;Uncertainty;Sensitivity;Bayesian theory;M odel test

U448．22

A

10．3969/j．issn．1003-1995．2016．12．03

1003-1995(2016)12-0009-03

(責任審編趙其文)

2016-08-03;

2016-09-30

張正陽(1987—)，男，博士研究生。