適當“越規”,啟迪創新
鄧林樹
摘 要: 啟迪學生的創新意識,要適當跨越封閉之“規”、定勢之“規”、常規之“規”。
關鍵詞: 跨越 封閉之“規” 定勢之“規” 常規之“規” 啟迪創新
創新意識是數學核心素養之一。《數學課程標準(2011年版)》指出:“創新意識的培養是現代數學教育的根本任務,應體現在數學教與學的過程之中。”但是當前數學課堂教學常常被封閉之“規”、定勢之“規”、常規之“規”所約束,學生的創新意識、創新思維、創新能力很難真正得到培養。因此,我強烈呼吁:不妨來一些“越規”之舉,為學生提供創新契機,挖掘他們的創新潛能。
一、適當跨越封閉之“規”,在開放中啟迪創新意識
傳統練習題條件完備,一題一答,不利于學生創新意識形成,我們把它稱做封閉題。這里的“開放”意指開放題,它是對封閉題而言的,指那些條件不足需補充、條件多余需選擇、答案不確定、解法多樣的題。所以在小學數學教學中如適當跨越“封閉”之“規”的約束,設計一些開放題,對啟迪學生的創新意識是大有裨益的。一方面給每個學生提供獲得成功的機會,促進不同程度學生在數學上得到不同程度的發展。另一方面為學生提供發散的空間,培養學生思維的發散性和創新性。
1.條件開放
例1:草地上有雞45只,鴨比雞多28只,鵝比鴨少30只,雞和鴨一共有幾只?
例2:果園里種有桃樹和梨樹,桃樹有75棵,_________________,這兩種果樹一共有多少棵?(補充條件并解答)
例1有3個條件,通過分析可知“鵝比鴨少30只”是多余條件。例2這種形式的問題從一年級到六年級都適用,可以幫助學生形成“看問題,想條件”的思路,只要從補充的條件中直接或間接地知道梨樹的棵數就行了,但是隨著學習的進展要逐步提高補充條件的要求。一開始是補上只需一步計算的條件,然后是補上兩步、三步計算的條件。如梨樹有25棵;梨樹比桃樹多10棵;桃樹比梨樹少25棵;梨樹的棵數是桃樹的2倍;桃樹的棵數是梨樹的3倍;梨樹棵數是桃樹的1/3;桃樹的棵數是梨樹的3/4;梨樹和桃樹棵數的比是4∶3;梨樹比桃樹的3倍多10棵……
條件開放題能引導學生從不同角度思考問題,通過補充條件、從眾多已知條件中排除表面現象的干擾,抓住問題的本質,篩選出有用的條件,高效、簡潔地解決問題,促進學生思維深刻性、創造性地發展。
2.結果開放
例3:某班男生30人,女生15人,________________________________?(提出一個數學問題并解答)
例4:一個長方體紙盒,長40厘米,寬25厘米,高10厘米。________________________________?(提出一個數學問題并解答)
這樣的題給了學生自主選擇的空間,他們能充分利用已知信息進行分析,從不同角度發現并提出各種各樣的問題,提出的問題同樣可以形成遞進發展系列,可以是一步計算的問題,也可以是兩步、三步計算的問題,還可以是帶附加條件的問題,如這個紙盒最多可以裝入多少個棱長3厘米的正方體木塊,等等。
3.方法開放
例5:修一條長1200米的路,3天修了這條路的1/5,剩下的需要幾天修完?(用多種方法解答)
通過這類題訓練,可以引導學生用同一知識從不同角度觀察和思考問題,形成不同的解題思路,也可以引導學生用不同的知識剖析數量關系,創造性地解決問題。如例5,可以先求出剩下的米數和每天修的米數,再用“剩下的米數÷每天修的米數”,于是有解法:(1200-1200×1/5)÷(1200×1/5÷3)或1200×(1-1/5)÷(1200×1/5÷3);也可以用“全長÷每天修的米數-已修的天數”,列式為1200÷(1200×1/5÷3)-3;還可以用解工程問題的思路,把全長“1200米”看作單位“1”,用“工作總量÷工作效率”求出工作時間,列式為(1-1/5)÷(1/5÷3)或1÷(1/5÷3)-3;最簡潔的解法是由“3天修了這條路的1/5”聯想到“3天就是總時間的1/5”,列式為3÷1/5-3。
二、適當跨越定勢之“規”,在變通中發展創新思維
人們在理解知識的過程中由于習慣運用某種思維方式,便會產生一種定式心理。這種定式心理會嚴重妨礙人們的創造性思維活動。如果不克服這種定式心理,思維就不會活躍,創新意識就不易產生。所以教學中教師要幫助學生跨越定式之“規”,激活他們思維的火花,讓他們學會從不同角度思考問題,解決問題。請看下面的例子:
例6:右圖中正方形的面積是10dm2,圓的面積是( )dm2。
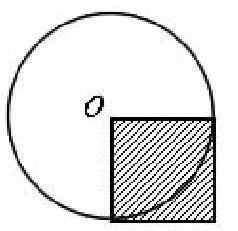
此題一出,學生議論紛紛:“半徑都不知道,怎么求圓的面積呢?”“會不會數據搞錯了,正方形的面積可能是9dm2?”平時教學中很喜歡用絕對化的語言,如“要求圓的面積,必須知道半徑”。于是學生就形成一種思維定式——知道半徑才能求圓的面積,所以學生的這種議論是一種必然。按照習慣,知道圓的半徑,可以根據圓面積計算公式s=πr2求圓的面積,但這里不知道圓的半徑。從圖中可以看出,圓的半徑是正方形的邊長,正方形的面積是10dm2,對于小學生來說,還無法求出它的邊長。由此看來,先求半徑再求面積的路子行不通。這時教師要引導學生打破思維定式,另辟蹊徑。因為圓的半徑是r,則正方形的面積可以表示成r2,r2=10,所以圓的面積s=πr2=3.14×10=31.4(dm2)。知道r2同樣可以求圓的面積。
三、適當跨越常規之“規”,在發散中激發創新潛能
在平時教學中教師比較重視常規解法,但常規思維有時會束縛學生思維潛能的發揮,所以,教師要注意引導學生打破常規思維束縛,變換角度思考、分析,創造性地解決問題。請看下面的例子:
例7:一根鐵絲,正好可圍成邊長為10㎝的正方形。如果把它圍成長15㎝的長方形,寬應是多少?
當學生按常規思路列出(10×4-15×2)÷2,10×4÷2-15等算式后,引導學生進行發散思維,掌握特殊的解題思路。如有的學生想:正方形兩條邊的和正好是長方形一條長與一條寬的和,去掉一條長就得到一條寬,可以列式為10×2-15。還有的學生這樣想:圍成的長方形的長比正方形的邊長長多少,那么長方形的寬就比邊長短多少,于是列式為10-(15-10)。這兩種思路擺脫了思維的常規、保守狀態,培養了學生的發散思維,體現了思維的創造性。
啟迪學生的創新意識,激活創新思維,培養創新能力是現代教育的出發點和歸宿,是全面實施素質教育的要求。數學教師應寓創造于數學課堂教學之中,把培養學生的創新意識放在第一位。

