身管內膛參數化模型及其磨損有限元模型的生成方法

丁傳俊， 張相炎， 劉寧

(南京理工大學 機械工程學院， 江蘇 南京 210094)

身管內膛參數化模型及其磨損有限元模型的生成方法

丁傳俊， 張相炎， 劉寧

(南京理工大學 機械工程學院， 江蘇 南京 210094)

為了精確地建立磨損內膛有限元模型，提出分片拼接法，建立身管內膛的參數化實體模型；提出節點偏移法，構建磨損程度不同的內膛有限元模型；通過搭建磨損內膛的彈炮耦合模型，并計及磨損內膛體積增大量，采用熱固耦合有限元法分析了火炮內彈道膛壓和彈丸初速的退化過程。通過對比仿真結果和實驗數據，驗證了上述建模方法的正確性。該研究不僅對身管的設計和分析具有參考意義，也可以為火炮內彈道的性能退化提供評估方法。

兵器科學與技術； 內膛； 實體模型； 有限元模型； 彈炮耦合； 內彈道； 磨損

0 引言

火炮發射過程中，身管和彈丸的耦合作用對其隨后外彈道過程有著重要的影響。由于發射時身管內膛表面要承受高溫高壓燃氣的燒蝕、沖刷和彈帶的擠壓、摩擦等作用，多發射擊后身管內膛將會出現磨損。這種幾何尺寸上的退化將會導致后續發射過程中內膛壓力異常、彈丸初速下降、彈丸飛行不穩定等現象，從而使火炮的戰術技術指標下降[1-2]。

近年來，國內外多位學者對彈炮耦合過程及彈炮耦合退化內彈道進行了研究，并取得了許多有價值的研究成果。文獻[3-4]基于分割策略將身管分為多段，采用映射掃描和拼接的方法，建立身管有限元模型并研究了彈炮接觸模型；文獻[5-6]通過建立身管、坡膛模型，基于有限元軟件Abaqus研究了彈炮耦合模型；文獻[7-9]基于梁理論，研究了剛性彈丸的軸向運動對身管振動的影響；文獻[10]通過建立陶瓷內膛熱力耦合有限元模型，研究了陶瓷內膛的彈炮耦合內彈道模型；文獻[11-12]通過統計身管磨損數據研究了身管磨損量和內彈道性能退化之間的關系，并建立二者之間的多項式模型；文獻[13]通過觀察彈帶材料的表層組織，探討了彈帶膛內熱軟化機理。

然而，當前彈炮耦合研究中至少有兩個難點沒有得到很好解決：1)身管內膛的實體模型和有限元模型難以精確地建立，其原因在于膛線作為空間螺旋體，其深度和膛線的軸向長度相差很大；2)內膛磨損量沿身管軸向分布不均且量值較小，若先建立實體模型則難以高效地建立磨損身管的有限元模型。

有鑒于此，本文基于某小口徑自動炮身管的實際尺寸，利用Python語言編制了該炮身管內膛的簡化型實體模型，并在有限元程序中生成其有限元模型；通過統計該型自動炮內膛實際磨損量，使用Python語言編寫了內膛有限元網格節點偏移程序，實現了磨損內膛有限元模型的構造；基于經典內彈道方程，通過編寫推力子程序、摩擦力子程序，使用商用有限元軟件Abaqus計算了該身管的熱力耦合型內彈道過程；綜合以上成果并將內膛體積擴大量計算公式整合到內彈道子程序中，計算了該型自動炮的退化內彈道參數并解釋了內彈道性能退化的原因。

1 身管參數化建模

研究當前身管有限元模型的構造過程發現，大多數研究人員首先使用三維建模軟件(UG、SolidWorks等)建立身管的實體模型，然后將實體模型導入到網格軟件中，根據需要進行模型簡化后再進行網格劃分等前處理工作。由于軟件兼容性問題，三維實體模型導入網格軟件后經常會發生精度問題，導致膛線這類實體構造失敗。例如，在文獻[14]中先使用Matlab計算了膛線控制點的坐標，然后將點坐標導入建模軟件中生成膛線的多段曲線，再將此曲線導入到有限元前處理軟件Hypermesh中，通過建立膛線截面并沿上述多段曲線掃描生成了單根膛線的有限元模型。本質上來說這種方法跳過了實體模型導入網格前處理軟件這一步驟，但操作過程比較復雜。

商用有限元軟件Abaqus內嵌了Python程序語言，使用該語言不僅可以快捷地調用Abaqus前后處理命令，還可以自行編制其他命令以實現Abaqus沒有的功能，這就為復雜模型的構造提供了可能。因此，本文提出一種在Abaqus內部利用Python語言參數化建模的方法，使用這種方法在構造身管時可以先不考慮坡膛和膛線起始部，其思路如下：

1)在建模模塊中，根據身管內膛陽線和陰線的具體參數使用(1)式計算身管截面控制點的空間坐標(見圖1(a))：

(1)

式中：Rc和Rb分別為內膛控制點半徑(陽線和陰線)和身管外壁控制點半徑；α0為控制點的初始定位角；θ為膛線的纏角；M為常數，用來控制身管的幾何精度，在當前研究中設定為120(每100 mm身管在長度上將劃分120個構建線框截面)；i(i= 0, 1, 2,…,Lx×M) 是構建線框截面的次序，Lx為身管的軸向長度(單位為mm，從內膛圓柱部算起)除以100.

圖1 身管建模過程Fig.1 Modelling process of gun barrel

2)使用圓弧和直線連接以上點的坐標，生成身管內膛的線框截面,共計(Lx×M)個(見圖1(b))。

3)在兩個截面之間建立直線或者樣條曲線，并沿該線拉伸截面創建放樣實體,共計(Lx×M-1)個(見圖1(c))。

4)將創建的實體導入到Abaqus的裝配模塊，旋轉復制N份(條)并做布爾融合運算生成身管(見圖1(d))。整個建模過程如圖1所示，編程人員可以自行改變基本參數以建立任意尺寸、纏角和膛線數量的身管，還可以根據需要修改代碼建立漸速膛線和混合膛線身管。

圖2即為使用該方法建立的23 mm (10條膛線，螺旋角7.16°)和130 mm (40條膛線，螺旋角6.0°)身管內膛實體模型，從圖2中可以看出，由于模型中的各個獨立分段在幾何形式上保持一致，所以可以使用結構化網格方法直接生成身管的有限元模型且網格質量較高。事實上這種方法可以稱為“分段拼接法[4]”，但基于參數化建模的思維，使該方法不僅可以提高建模精度和自由度，還可以為后續網格的生成提供便利。實踐發現，參數M設定的越大(默認值為120)，身管實體模型精度越高，但運算時間也會相應增加。

圖2 身管三維實體模型Fig.2 3D solid model of gun barrel

2 磨損身管有限元模型的構造策略

在研究退化內彈道的過程中，本文根據多根身管的內膛測量結果(測量起點為內膛圓柱部，結果如圖3所示)，分析了身管磨損的4個不同階段并得到如下結論：1)身管磨損后其內膛幾何尺寸發生變化，不僅沿身管軸向上磨損量分配不均，而且陽線和陰線的磨損量也不一樣；2)由于磨損量只是膛線深度的幾分之一，甚至有些地方沒有磨損，因此無法高效地構造實體模型并建立磨損身管的有限元模型。同時本文發現，由于建模方法上的限制，大多數研究人員雖然能夠準確地測量身管各個區段的磨損量，但是在計算時只考慮磨損最大處的磨損量(文獻[12]稱該點為磨損特征點)。事實上，由于身管磨損后內彈道的起始條件已經發生變化，如果只將磨損最大處的磨損量納入計算，其計算結果不具有較強的說服力。

圖3 內膛陽線和陰線的直徑Fig.3 Land and groove diameters of gun bore

因此，本文基于已建立的標準內膛實體模型和有限元模型，使用Python語言編程構造了多根磨損程度不同的身管有限元模型，其思路如下：

圖4 節點偏移流程Fig.4 Flow chart of node-offset algorithm

1)統計多根身管的磨損量，并建立內膛磨損量數據集W(d,n,P)，其中d代表陽線或者陰線的直徑，n為射擊發數，P為內膛圓柱部起點和該節點之間的距離；

2)建立內膛表面的陽線和陰線節點集合S，建立搜索球，使用搜索半徑R搜索表面節點集S下方的其他節點，并計算磨損方向矢量(即節點偏移矢量)；

3)根據磨損數據集中數據計算該表面節點的磨損量(偏移量)，然后決定是偏移或是刪除該節點，其中針對集合S中任意節點P1(以及P1下面的節點P2、P3)的詳細操作過程可由圖4表示。

由于坡膛和膛線起始部都是基于去除材料法加工得到的，因此可采用上述方法構造無磨損身管的有限元模型，圖5即為使用該方法構造的身管內膛網格模型。有必要說明的是，經過多次實驗發現，上述構造策略使用0.8倍的節點間距作為節點刪除判據，可以防止生成很狹長的“薄層”網格和防止網格發生扭曲，因此該方法可以稱為具有自適應特性的“節點偏移法”。圖6為使用節點偏移法生成的4個磨損程度不同的身管內膛有限元模型。

圖5 節點偏移法生成的無磨損內膛有限元模型Fig.5 FE model of gun bore (without wear) based on node-offset algorithm

圖6 4個磨損階段的內膛有限元模型Fig.6 FE model of gun bore in four wear phases

3 磨損身管彈炮熱力耦合有限元模型的建立

根據23 mm航空自動炮彈丸的實際尺寸，本文對其進行必要的簡化后結合上文構造的身管分別建立了標準彈炮耦合模型和4個身管磨損程度不同的彈炮耦合模型。

3.1 基本假設

1)彈帶為各向同性材料，且熱物理性能參數(比熱容、熱導率、彈性模量)隨溫度變化而變化；

2)彈帶為彈塑性體，屈服強度服從Mises屈服準則，彈體為彈性體，身管設定剛體限制以節省計算成本；

3)彈丸、彈帶和身管初始溫度恒定(25 ℃)，且不考慮彈帶的自由對流換熱和輻射放熱；

4)身管磨損后，內膛截面保持幾何上的對稱性。

3.2 有限元模型

內膛部分由坡膛、膛線構成，彈丸部分由彈體和彈帶構成，彈帶和坡膛之間有一定的定位間隙。其中標準模型如圖7所示。彈炮耦合計算模型的相關設定和發射子程序的編寫過程詳見參考文獻[15]。

圖7 彈炮耦合有限元模型Fig.7 Assembled finite element model of projectile-barrel interaction

3.3 身管磨損后彈后空間體積增大量的計算

身管磨損后彈后空間比起無磨損身管有所增大，其任意時刻體積增大量ΔV可以表示為陽線和陰線斷面面積增大量沿彈丸軸向位移的積分，因此ΔV的表達式為

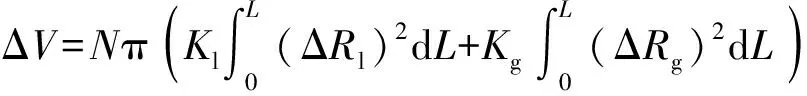
(2)

式中：N、Kl、Kg、ΔRl、ΔRg分別為膛線數量、陽線角度系數、陰線角度系數、陽線半徑增量、陰線半徑增量；L為任意時刻彈丸的行程。在編程時可以使用復合辛普森法求解該表達式，并將其計算結果加到文獻[15](10)式和(11)式第3式的分母中。

4 模型驗證及結果分析

4.1 模型驗證

為了驗證上文建模方法的準確性，本文首先在三維建模軟件中對所建立的內膛實體模型進行坐標檢查和尺寸測量；至于有限元模型，本文將無磨損彈炮耦合模型的計算結果和彈道炮修正結果[1]進行了對比。計算結果如圖8所示，炮口速度和最大膛壓分別為707.7 m/s和340.3 MPa，和彈道炮修正結果相比，最大膛壓增大了6.28% (318.9 MPa) ，炮口速度減小了0.36% (710.2 m/s)，且壓力最大值點提前。出現這種結果的原因在于，文獻[1]利用彈道炮測試值符合計算壓力曲線時并沒有考慮拔彈力等因素。和普通實驗測試結果相比，本文模型最大膛壓增大了3.8%(327.8 MPa)，出膛速度只增大了0.28%(705.0 m/s)。

圖8 未磨損身管的內彈道壓力和彈丸速度Fig.8 Bore pressure of barrel (without wear) and projectile velocity

圖9為無磨損有限元模型子程序輸出的彈丸運動阻力、彈帶摩擦功和塑性功。從圖9可以看出：對于藥筒定裝式炮彈，在內彈道起始階段彈丸的阻力基本為拔彈阻力；隨著膛壓的升高、彈丸逐漸前移，彈丸將同時受到拔彈阻力、彈帶接觸變形阻力、彈帶摩擦阻力等阻力的共同作用，在0.35 ms時刻，運動阻力達到了最大值45 481.8 N. 完全擠入膛線后，彈帶不再有塑性變形，運動阻力因只剩下摩擦阻力而迅速下降；彈帶的塑性功在擠進完成后維持114.6 J不變，但摩擦功持續增長并達到582.9 J，和文獻[1]計算結果相差4.01% (607.3 J)。文獻[1]使用彈丸動能乘以一個經驗系數作為摩擦功的估計值，并不能反映計算摩擦功的累積過程。而本文的計算模型充分考慮了摩擦系數隨溫度的變化關系、銅質彈帶的摩擦剪應力上限等情況，計算精度相對更高，具體情況詳見文獻[15]。彈帶的塑性功約為摩擦功的25%，這說明在內彈道初期塑性功是不可忽略的。

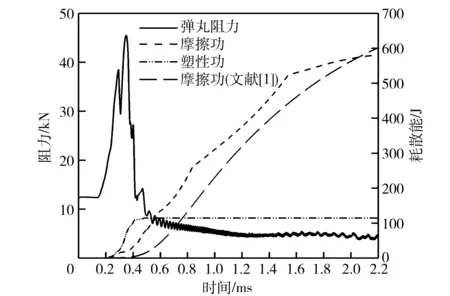
圖9 彈丸運動阻力、摩擦功與塑性功Fig.9 Motion resistance, friction work and plastic work of projectile

4.2 身管內膛磨損對彈炮耦合內彈道的影響

本文基于內膛尺寸的實測數據，使用上述節點偏移方法分別構造了磨損初期(射擊500發)、中期(射擊2 000發)、中后期(射擊4 000發)、末期(射擊6 000發)的身管有限元模型。由于難以找到發射數量完全相同的身管，所以同一磨損階段各個身管磨損程度并不一致，因此在構建磨損數據集時取磨損尺寸的較大值。計算結果如圖10和圖11所示。

圖10 身管磨損后內彈道壓力和彈丸速度Fig.10 Bore pressure and projectile velocity of worn barrels

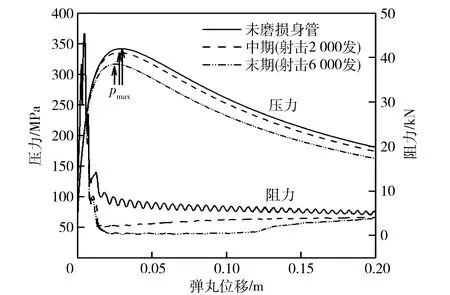
圖11 膛壓和阻力隨彈丸位移的變化曲線Fig.11 Variation of bore pressure and projectile motion resistance with displacement of projectile

使用上述磨損身管所建立的彈炮耦合模型進行計算可以發現，和標準模型相比，4個磨損階段最大膛壓分別下降了1.08% (337.3 MPa)、1.60% (335.5 MPa)、3.95% (327.5 MPa)、7.10% (316.6 MPa)，炮口速度分別下降了0.39% (702.8 m/s)、0.97% (698.7 m/s)、1.90% (692.1 m/s)、3.20% (682.5 m/s)。使用兩門發射數量接近6 000發的火炮進行實驗，結果顯示彈丸的炮口速度分別為692.0 m/s、690.0 m/s，和壽命之初相比下降量分別為1.83%、1.82%. 本文的計算結果比實驗結果大，其原因是本文在統計身管的磨損量時，取的是磨損尺寸中的較大值。最后基于以上數值分析結果，本文給出了該型自動炮的內彈道性能退化預測公式：

p(n)=-3.32×10-10n3-1.22×10-7n2-

1.87×10-3n+339.4，

(3)

v(n)=-1.63×10-10n3+1.40×10-6n2-

6.65×10-3n+707.0.

(4)

圖11對比了未磨損身管、壽命中期和壽命末期身管沿彈丸移動方向上的膛壓和彈丸阻力。身管磨損后最大膛壓點有向炮尾移動的趨勢，和標準模型相比中期和末期的最大壓力點分別向炮尾方向移動了1.07 mm、3.70 mm. 身管壽命末期彈丸阻力的峰值只下降0.37% (45 313 N)，但在膛壓最大點附近，彈丸阻力下降明顯(最大下降量為89%)。因此針對該型火炮，本文給出身管磨損后膛壓和速度下降的主要原因——膛壓最大點附近的燒蝕磨損使內膛尺寸擴大，從而導致了彈丸運動阻力降低、彈后空間擴大迅速，最終使得最大膛壓和炮口速度降低。

基于以上無磨損模型和4個磨損模型的建模和仿真計算，并且將結果與標準內彈道、射擊實驗數據進行對比，驗證上述建模方法和節點偏移方法的準確性。因此，本研究的下一步工作是標準化上述建模方法并統計其他身管的磨損數據，建立更為普遍的磨損量分布趨勢并開展實驗驗證上述研究結論的準確性。

5 結論

1)基于參數化建模的思想，使用“分段拼接法”可以實現身管內膛實體模型及其有限元模型的構造，結果顯示該方法具有建模速度快、精度高等特點。

2)基于內膛實測數據，使用“節點偏移法”可以生成任意磨損程度的內膛有限元模型，內膛網格即使在節點偏移之后也具有較高的質量，這顯示了該方法的適應性；通過搭建彈炮耦合仿真模型，并計及磨損內膛的體積擴大量，進一步驗證了該建模方法的正確性。

3)對于本文研究的火炮，內膛磨損后彈丸運動阻力的峰值下降不顯著，膛壓最大點附近彈丸運動阻力的大幅度減小使彈后空間迅速擴大才是導致內膛壓力下降和炮口速度下降的主要原因。

References)

[1] 何志強, 黃守仁, 李載弘. 航空自動武器設計手冊[M].北京: 國防工業出版社, 1991: 190-216. HE Zhi-qiang, HUANG Shou-ren, LI Zai-hong.Handbook for airborne automatic weapon design[M]. Beijing: National Defense Industry Press, 1991:190-216. (in Chinese)

[2] 丘爾巴諾夫 E B. 擠進時期內彈道學與擠進壓力計算[M].楊敬榮, 譯. 北京: 國防工業出版社, 1997: 115-121. Qierbarov E B. Interior ballistics and engraving force calculation during engraving of projectile[M]. YANG Jing-rong, translated. Beijing: National Defense Industry Press, 1997: 115-121. (in Chinese)

[3] 葛建立, 楊國來, 陳運生, 等. 基于彈塑性接觸/碰撞模型的彈炮耦合問題研究[J]. 彈道學報, 2008, 20(3): 103-106. GE Jian-li, YANG Guo-lai, CHEN Yun-sheng, et al. A study on projectile-barrel coupling problem based on elastoplastic contact/impact model[J]. Journal of Ballistics, 2008, 20(3): 103-106. (in Chinese)

[4] 劉雷, 陳運生, 楊國來, 等. 基于接觸模型的彈炮耦合問題研究[J]. 兵工學報, 2006, 27(6): 984-987. LIU Lei, CHEN Yun-sheng, YANG Guo-lai, et al. A study on the projectile- barrel coupling based on contact model[J]. Acta Armamentarii, 2006, 27(6): 984-987. (in Chinese)

[5] 樊黎霞, 何湘玥. 彈丸擠進過程的有限元模擬與分析[J].兵工學報, 2011, 32(8): 963-968. FAN Li-xia,HE Xiang-yue. Finite element simulation and process analysis of projectile entering into barrel[J]. Acta Armamentatii, 2011, 32(8): 963-968. (in Chinese)

[6] 孫河洋, 馬吉勝, 李偉, 等. 坡膛結構變化對火炮內彈道性能影響的研究[J]. 兵工學報, 2012, 33(6):669-675. SUN He-yang, MA Ji-sheng, LI Wei, et al. Study on influence of bore structure on gun's interior ballistic performances[J]. Acta Armamentarii, 2012, 33(6):669-675. (in Chinese)

[7] 劉寧, 楊國來. 移動質量作用下軸向運動懸臂梁振動特性分析[J].振動與沖擊, 2012, 31(3): 102-105. LIU Ning, YANG Guo-lai. Vibration property analysis of axially moving cantilever beam considering the effect of moving mass[J]. Journal of Vibration and Shock, 2012, 31(3): 102-105. (in Chinese)

[8] 蘇忠亭, 徐達, 李曉偉, 等. 小口徑火炮彈炮耦合動態響應有限元時程分析[J]. 振動與沖擊, 2012, 31(23): 104-18. SU Zhong-ting, XU Da, LI Xiao-wei, et al. Finite-element time-history analysis for dynamic response of small-caliber guns with projectile-barrel coupling[J]. Journal of Vibration and Shock, 2012, 31(23): 104-18. (in Chinese)

[9] 陳世業, 王良明, 史偉. 基于虛擬體的身管多體動力學模型研究[J]. 彈道學報, 2012, 24(4): 62-66. CHEN Shi-ye, WANG Liang-ming, SHI Wei. Research on multi-body dynamics model of barrel based on virtual substance[J]. Journal of Ballistics, 2012, 24(4): 62-66. (in Chinese)

[10] Huang X, Garner J, Conroy P. Thermal and ballistic dynamic analyses for gun ceramic nozzles[J]. Materials and Manufacturing Processes, 2006,21 (5/6): 602-611.

[11] 劉怡昕, 王桂玉. 由炮膛磨損規律確定火炮初速減退量[J].兵工學報, 2007, 28(1): 7-9. LIU Yi-xin, WANG Gui-yu. Determination of muzzle velocity loss by law of bore wear[J]. Acta Armamentarii, 2007, 28(1): 7-9. (in Chinese)

[12] 田桂軍. 內彈道燒蝕磨損及其對內彈道性能影響的研究[D]. 南京:南京理工大學, 2003: 44-62. TIAN Gui-jun. Researches on the wear and erosion of bore and its influence to interior ballistic performance[D]. Nanjing: Nanjing University of Science and Technology, 2003: 44-62. (in Chinese)

[13] 殷軍輝, 鄭堅, 倪新華, 等. 彈丸膛內運動過程中彈帶表層熱軟化機理分析[J]. 彈道學報, 2012, 24(2): 106-110. YIN Jun-hui, ZHENG Jian, NI Xin-hua, et al. Mechanism analy-sis of thermal softening of rotating band surface in process of projectile motion in bore[J]. Journal of Ballistics, 2012, 24(2): 106-110. (in Chinese)

[14] 張振輝. 末制導炮彈與火炮身管相互耦合機理及適配性技術[D]. 南京:南京理工大學, 2012: 46-49. ZHANG Zhen-hui. The mutual interaction mechanism between the terminal guided projectile and barrel[D]. Nanjing: Nanjing University of Science and Technology, 2012: 46-49. (in Chinese)

[15] 丁傳俊, 張相炎. 基于熱力耦合有限元模型的彈帶擠進過程及內彈道過程的仿真研究[J]. 兵工學報, 2015, 36(12): 2254-2261. DING Chuan-jun, ZHANG Xiang-yan. Simulation study of bearing band engraving process and interior ballistic process based on thermo-mechanical coupling FEA model[J]. Acta Armamentarii, 2015, 36(12): 2254-2261. (in Chinese)

A Parametric Modeling Method for Gun Barrel and a Meshing Generation Strategy for Worn Barrel

DING Chuan-jun, ZHANG Xiang-yan, LIU Ning

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

In order to accurately build the finite element model of worn gun barrel, a piecewise-connection algorithm is designed to generate parametric 3D solid model of bore, and a node-offset algorithm is proposed to construct the finite element analysis model of bore with different wear degrees. Based on the projectile-barrel interaction model of worn barrel, and taking account of the increment in bore's volume, the interior ballistic process is simulated by the thermo-mechanical coupling finite element method. And the main reason of degradation in muzzle velocity and chamber pressure for a 23 mm gun is also studied. The simulated result matches with the experimental data, which verifies the correctness of the proposed modeling method and meshing strategy. The present study not only has important guiding significance for the design and analysis of gun barrel, but also provides an evaluation method for the performance degradation of interior ballistic process.

ordnance science and technology; gun bore; 3D solid model; finite element model; projectile-barrel interaction; interior ballistics; wear

2016-03-23

江蘇省自然科學基金項目(BK20140789)

丁傳俊(1986—)，男，博士研究生。E-mail:381667117@qq.com； 張相炎(1957—)，男，教授，博士生導師。E-mail:xyzhang@mail.njust.edu.cn

TJ301

A

1000-1093(2016)12-2212-08

10.3969/j.issn.1000-1093.2016.12.005