一種RaptorQ碼的模式選擇解碼算法
李 越,張立軍,李明齊,朱秋煜
(1.上海大學,上海 200444;2.中國科學院 上海高等研究院,上海 201210)
?
一種RaptorQ碼的模式選擇解碼算法
李 越1,2,張立軍2,李明齊2,朱秋煜1
(1.上海大學,上海 200444;2.中國科學院 上海高等研究院,上海 201210)
針對 RaptorQ 碼解碼復雜度高的問題,提出了一種模式選擇解碼(MSD)算法。該方法結合優化失活解碼高斯消元(OIDGE)算法與快速降維解碼(DRFD)算法的優點,綜合考慮了信道的實際丟包情況與不同解碼算法的效率,根據計算所得丟包率,選擇合適的解碼算法。在嵌入式系統上進行了實驗,結果表明,該算法在不同丟包率情況下可以自適應地選擇合適的解碼算法,提高了RaptorQ碼的解碼效率。
應用層FEC;噴泉碼;RaptorQ碼;高斯消元解碼
近幾年互聯網數據流量大幅度增長,為了有效地支持流媒體傳輸和文件分發,3GPP-MBMS和DVB-H IPDC都將噴泉碼作為應用層的前向糾錯(AL-FEC)方案[1-2]。LT碼[3]是第一個實用的噴泉碼編碼方案。Raptor碼[4]通過將LDPC碼與LT碼級聯,降低了解碼開銷。RaptorQ碼是一種定義在伽羅華域 GF(256)上的Raptor碼,它繼承了所有Raptor碼的基本屬性和編解碼處理流程,同時能降低解碼失敗概率,但在編解碼的過程中需要對預編碼矩陣進行復雜的求逆運算,導致其解碼復雜度較高。IETF RFC 6330[5]根據碼約束矩陣具有稀疏性的特點,提出了失活解碼高斯消元算法(Inactivation Decoding Gaussian Elimination, IDGE),文獻[6]在此基礎上提出了優化失活解碼高斯消元(Optimized Inactivation Decoding Gaussian Elimination, OIDGE)算法,該算法通過簡化解碼步驟和對行選擇方法進行優化,提高了解碼計算的效率。文獻[7]首次提出增量解碼(Incremental Decoding)的概念,另外,文獻[8]和[9]提出了兩種增量高斯消元解碼算法,結果均表明增量解碼技術優于重新解碼的方法。文獻[10]提出一種降維快速解碼(Dimensionality Reduced Fast Decoding, DRFD)算法,該算法通過降低矩陣維數,降低了解碼復雜度,但算法的性能受信道符號刪除率的影響較大。在信道符號刪除概率較高(>0.1)時,該算法的解碼速度明顯下降。
雖然OIDGE算法在很大程度上降低了解碼的計算復雜度,但是在嵌入式系統上仍然難以滿足接收系統的實時性要求。而DRFD算法的性能受信道符號刪除率的影響較大,在高丟包率信道條件下的性能反而下降。因此本文對RaptorQ碼的解碼機制進行改進,在OIDGE算法與DRFD算法的基礎上,提出了一種RaptorQ碼的模式選擇解碼(Mode Selection Decoding, MSD)算法,該方法綜合考慮了信道的實際丟包情況與兩種解碼算法的效率,根據當前接收到的編碼數據塊中丟失的數據包數目占總數據包數目的百分比,選擇對應的解碼模式。實驗結果表明,該算法可以在不同丟包率情況下自適應地選擇合適的解碼算法,在低丟包率時選擇DRFD解碼,在高丟包率時選擇OIDGE解碼,提高了RaptorQ碼的解碼速度。
1 RaptorQ碼的解碼
RaptorQ碼由預編碼和LT編碼級聯構成的線性碼。編碼分為預編碼和LT編碼兩個過程。預編碼過程通過一個預編碼矩陣A生成中間符號,首先將K個源符號增補得到K′,對應K′個源符號向量,接著進行預編碼產生L(L=K′+S+H)個中間符號,其中K′表示源符號,S表示LDPC符號,H表示HDPC符號。最后由中間符號進行LT編碼產生最終的編碼符號[5]。
RaptorQ 的解碼過程相當于,通過對預編碼矩陣A進行高斯消元求逆矩陣,還原出中間符號向量。其過程可表示為
C=A-1·D
(1)
式中:D表示接收到的編碼符號向量;C表示恢復出的中間編碼符號向量。然后對中間符號向量C進行LT編碼來恢復出源數據符號向量[7]。
1.1 OIDGE解碼算法
文獻[4]的增強高斯消元解碼算法(EGE)認為,如果標準的高斯消元過程進行成功,可以直接進行回代,解碼成功;如果高斯消元過程失敗,則重新執行高斯消元步驟,直至成功解碼。
文獻[5]中失活高斯消元算法常被叫做IDGE算法。它利用置信度傳播的方法尋找出可以解碼的符號,同時生成一個與A同維度的矩陣X,用來記錄在A矩陣上進行的行/列變換操作。該算法在求解預編碼矩陣的逆的過程中,分別進行置信度傳播、高斯消元和前向消元的步驟。由于該算法需要對矩陣X進行矩陣乘法運算尋找失活符號,反而增加了計算量。
針對這一問題,在文獻[6]中提出一種優化算法——OIDGE算法。該算法避免了對矩陣X的乘法運算,直接對UM×u(upper)進行消元。雖然此時UM×u(upper)是稠密的,只需要消去在解碼輸出時用到的部分行即可,其他行不需要進行消元。由于省略了與X的乘法,A矩陣左上角仍為單位陣,故 OIDGE 算法只需3步即可完成矩陣A的逆運算。
文獻[5]提出增量解碼(Incremental Decoding)的概念,當高斯消元過程失敗時,將增加接收編碼符號的個數,以獲得行數足夠多的預編碼矩陣,保證預編碼矩陣的滿秩性。當解碼失敗時只需在解碼失敗矩陣的基礎上進行修補解碼,避免了需要從頭開始解碼而造成的解碼時延。
在運行頻率為1 GHz的Freescale ARM架構的嵌入式主板上測試了RaptorQ碼的解碼過程,對IDGE與OIDGE解碼算法中每個數據塊解碼的時間消耗進行比較。每個數據塊包含K個源符號,經過 RaptorQ 編碼后生成長度為N個編碼符號塊。結果如表1所示,其中K表示每個數據塊包含源符號的個數,T表示每個符號的字節長度。

表1 每個數據塊解碼時間消耗μs
1.2 DRFD算法
文獻[10]利用 RaptorQ 碼是系統碼的特性,提出一種降維快速解碼算法。該算法的原理是利用預先計算的逆矩陣,將解碼過程中對接收編碼約束矩陣的求逆轉化為對更小維數矩陣的求逆,以降低解碼復雜度。該算法的解碼效果與現有解碼算法等價。實驗結果表明,該算法降低了矩陣求逆的維度,在信道符號刪除概率較低(<0.1)時,該算法的解碼速度明顯高于現有算法,且算法復雜度遠低于IDGE算法。
DRFD算法的具體步驟是通過矩陣變換將求逆的對象由L×L維的預編碼矩陣A變換為r×r維矩陣Gx,其中r=K-s,s是一個數據塊中接收到的信息符號的個數,r是該數據塊中丟失的信息符號個數。在低丟包率的情況下,有r?L,因而復雜度降低。
在一個數據塊中,可以把接收到的L×T維符號矩陣D分解為D=D0+Dx,其中D0包含接收到的s個信息符號,Dx包含丟失的r個信息符號,其余部分為0。記S為接收到的信息符號組成的集合,R為丟失的信息符號組成的集合。注意到D=A·C,則接收到的r個修復符號可以表示為
E=GLT·C=GLT·A-1·(D0+Dx)=
G0·d0+Gx·dx
(2)
式中:r×s維矩陣G0=GLT·{A-1}i∈S;r×r維矩陣Gx=GLT·{A-1}i∈R;矩陣{A-1}i∈S和{A-1}i∈R分別代表從A-1中抽取對應于S和R的列組成的集合;s×T維矩陣d0={D0}j∈S和r×T維矩陣dx={Dx}j∈R分別代表從D0和DX中抽取對應于S和R的行組成的集合。從式(2)可得
(3)
其中A-1可預先求得,實際解碼過程中只需用高斯消元法對Gx求逆。
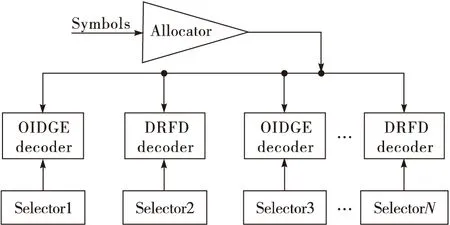
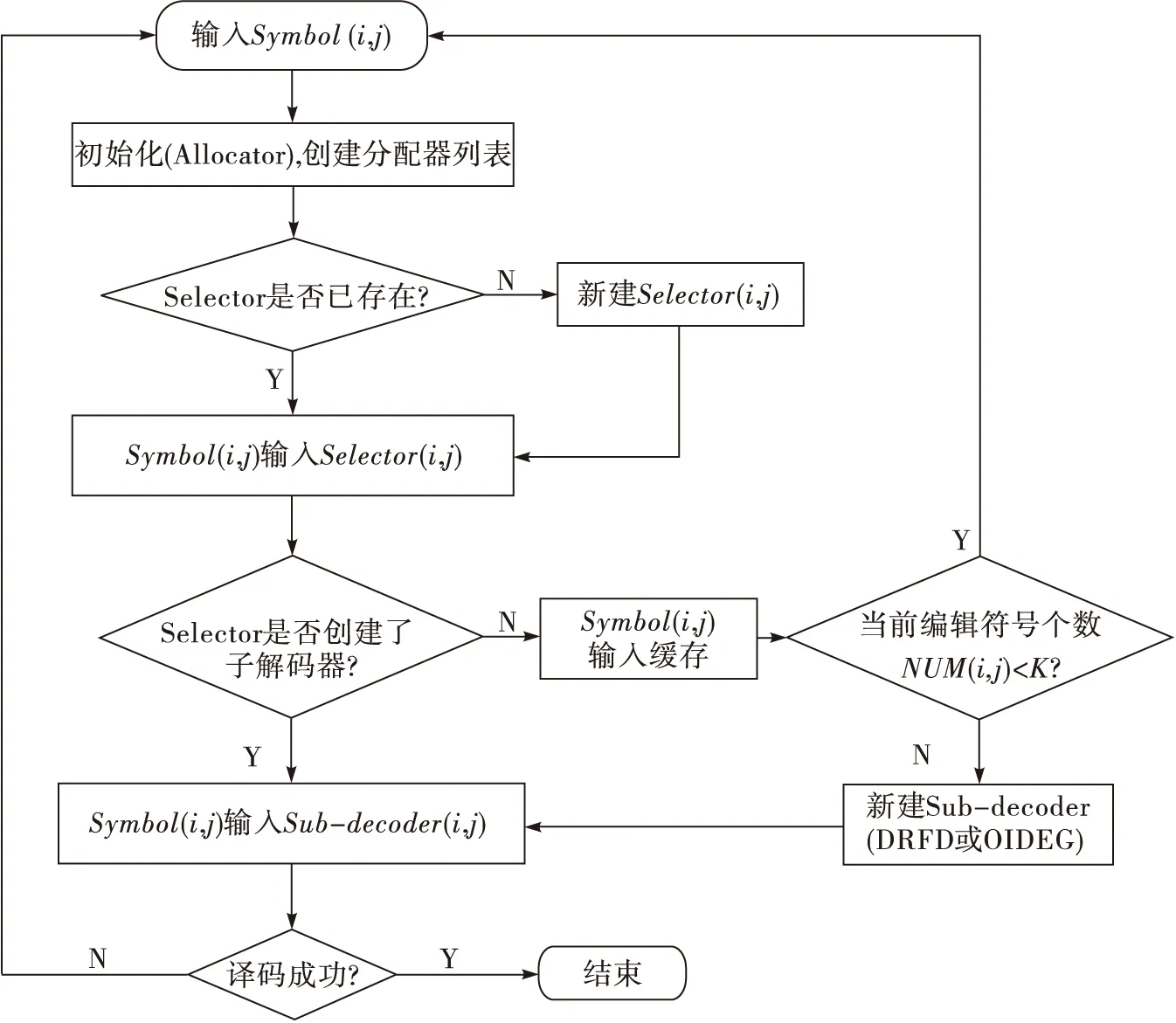
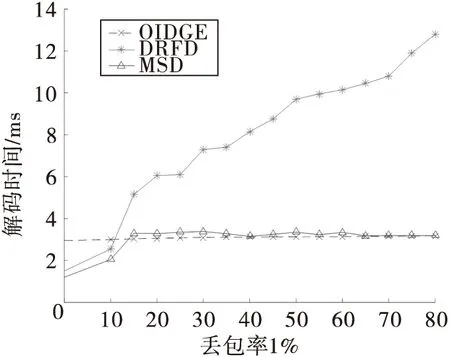
雖然總是有r≤K 2.1 解碼器的結構 為了提高RaptorQ碼的解碼效率,本節提出一種用于RaptorQ碼的模式選擇解碼(MSD)算法,該算法結合了OIDGE算法和DRFD算法的優點。如圖1所示,分配器Allocator為接收到的每一個數據塊分配一個選擇器Selector,并將接收到的符號按數據塊分別緩存在相應的選擇器中。選擇器根據接收到信息符號的數量來選擇解碼算法。 圖1 模式選擇解碼器 2.2 模式選擇解碼過程 模式選擇解碼算法流程圖如圖2所示。 圖2 模式選擇解碼流程圖 首先進行初始化。 第一步:生成選擇器。 接收一個編碼符號Symbol(i,j),它屬于第i個文件的第j個數據塊。分配器在已有的子解碼器列表中檢索(i,j),檢查是否有選擇器Selector(i,j)與之對應。若存在對應的Symbol(i,j),則將(i,j)輸入給它;若沒有對應的選擇器,則由分配器創建一個新的選擇器Selector(i,j),重置編碼符號個數NUM(i,j)=0,將Symbol(i,j)輸入給它,跳轉至第二步。 第二步:選擇器Selector(i,j)接收到符號Symbol(i,j)。 若該選擇器已創建子解碼器Sub-Decoder(i,j),則將符號輸入到該子解碼器,跳轉至第三步。若尚未創建子解碼器Sub-Decoder(i,j),則將符號存入緩存,記錄當前編碼符號個數NUM(i,j),若當前編碼符號個數NUM(i,j) 第三步:子解碼器解碼。 若解碼成功,則對序列號ESI=1:K輸出源符號,該數據塊解碼完畢,刪除選擇器Selector(i,j)和子解碼器Sub-Decoder(i,j) ;若解碼失敗,則跳轉至第一步進行增量解碼。 2.3 性能分析 在高斯消元法可以恢復源數據塊的情況下,失活解碼算法也能保證對其恢復,并且效率更高。失活解碼算法在第一步和第三步使用置信度傳播解碼,解碼時間是線性的。因此,在源數據塊范圍內,整個失活解碼過程解碼時間是線性的,采用IDGE/OIDGE算法[5-6],其復雜度是O(L2)。 DRFD算法使用降維變換降低了GE算法的矩陣的維數。該算法改變了傳統的兩步譯碼結構,無需先譯出中間符號,直接通過接收的編碼符號譯出丟失的源符號。雖然計算Gx=GLT·{A-1}i∈R的過程需要引入矩陣乘法和加法,在一定程度上增加了計算量。但矩陣GLT(i), i∈R為二進制稀疏矩陣,對A-1中的行進行異或操作即可計算出Gx,省去了GF(256)上的矩陣乘法。假設信道的丟包率為p,則矩陣GLT(i), i∈R的行數r約為pK,矩陣Gx的譯碼計算復雜度為O(pKL),L為中間符號的個數,略大于K。而對Gx的消元只能采用標準高斯消元算法,其復雜度是O(r3)[8],DRFD 算法整體的計算復雜度為O(p3k3)[8]。因此,在丟包率比較高的情況下,r值較大,后者的復雜度反而高于前者;在低丟包率的情況下,有r≤L,因而復雜度降低。 本算法在信道丟包率較低時的計算復雜度為O(r3),在信道丟包率大于10%左右時的計算復雜度為O(L2)。 算法驗證分別在PC機(64位處理器,Interl?CoreTM2 E7200 2.53 GHz)和Freescale ARM架構的嵌入式主板上進行。嵌入式主板采用飛思卡爾酷睿A9系列處理器,運行頻率為1 GHz。用C語言程序實現了RaptorQ碼的解碼過程,分別對OIDGE算法,DRFD算法與本文提出的MSD算法進行了測試。每個數據塊包含K=64個源符號,每個符號長度為T=1 024 byte,經過 RaptorQ 編碼后生成長度為N=80的編碼符號塊,然后在刪除信道上進行傳輸。接收端對接收到的編碼符號進行緩存和解碼。對每個數據塊重復多次進行上述過程,直到接收端成功解碼為止。這里開發了RaptorQ編譯碼算法庫,并把它集成到了開源項目上,用來實現符合FLUTE(File Delivery over Unidirectional Transport)協議的文件傳輸。其中發送端調用RaptorQ編碼,運行在一臺PC機上;接收端(嵌入式主板)調用RaptorQ解碼。通過測試,得出3種解碼算法的耗時圖如圖3所示。 圖3 OIDGE,DRFD,MSD算法的解碼時間 3條曲線分別代表了3種算法的解碼時間隨著丟包率變化的趨勢。結果顯示DRFD算法在丟包率低于10%的范圍內解碼時間比OIDGE短,但在其他范圍內耗時明顯增加,而OIDGE 解碼時間較平穩。MSD算法則結合了兩者的優點,在任何丟包率的情況下,都能在較短的時間內進行解碼。在5%丟包率時,MSD算法相對OIDGE算法的解碼時間減少了一半,在高丟包率時,兩者基本相等。實際解碼時間證明,編碼符號經過選擇器的時間可以忽略不計,不對解碼造成影響。 本文針對RaptorQ碼解碼復雜度高的問題,提出了一種模式選擇解碼算法,該方法綜合考慮了信道的實際丟包情況與不同解碼算法的效率,根據計算所得丟包率,選擇對應的解碼模式。實驗結果表明,該算法適用于嵌入式系統中的各種丟包率的場景,在一定程度上提高了RaptorQ碼的解碼效率。 [1] DVB transport of MPEG-2 TS based DVB services over IP based networks:ETSI T S. 102 034 V1.5.1[S].2014. [2] BOURAS C, KANAKIS N, KOKKINOS V, et al. Embracing RaptorQ FEC in 3GPP multicast services[J]. Wireless networks,2013,19(5): 1023-1035. [3] LUBY M. LT codes[C]// Proc. the 43rd Symposium on Foundations of Computer Science. [S.l.]:IEEE, 2002:271. [4] LUBY M, SHOKROLLAHI A, WATSON M, et al. RFC 5053: Raptor forward error correction scheme: Scheme for object delivery[R]. [S.l.]:IETF, 2007. [5] LUBY M, SHOKROLLAHI A, WATSON M, et al.RFC 6330, RaptorQ forward error correction scheme for object delivery[S].2011. [6] MLADENOV T, NOOSHABADI S, KIM K. Efficient GF (256) raptor code decoding for multimedia broadcast/multicast services and consumer terminals[J]. IEEE transactions on consumer electronics, 2012, 58(2):356-363. [7] KIM S, KO K, CHUNG S Y. Incremental Gaussian elimination decoding of raptor codes over BEC[J]. IEEE communications letters, 2008,12(4):307-309. [8] MLADENOV T, NOOSHABADI S, KIM K. Strategies for the design of Raptor decoding in broadcast/multicast delivery systems[J]. IEEE transactions on consumer electronics, 2010, 56(2): 423-428. [9] MLADENOV T, NOOSHABADI S, KIM K. Efficient incremental raptor decoding over bec for 3GPP MBMS and DVB IP-data cast services[J]. IEEE transactions on broadcasting, 2011, 57(2): 313-318. [10] 郭曉, 張更新, 徐任暉,等. 一種用于 RaptorQ 碼的降維快速解碼算法[J]. 電子與信息學報, 2015, 37(6): 1310-1316. 李 越(1992— ),女,碩士生,主研信道編碼; 張立軍(1974— ),助理研究員,主研視頻通信; 李明齊(1971— ),研究員,主研無線“三網融合”、4G/B4G關鍵技術、基于3GPP的軟件無線電; 朱秋煜(1964— ),教授,主研圖像處理、模式識別、計算機視覺、智慧城市、計算機應用。 責任編輯:薛 京 A mode selection algorithm for RaptorQ code decoding LI Yue1,2, ZHANG Lijun2, LI Mingqi2, ZHU Qiuyu1 (1.ShanghaiUniversity,Shanghai200444,China;2.ShanghaiAdvancedResearchInstitute,ChineseAcademyofSciences,Shanghai201210,China) Aiming at the problem of high complexity of decoding RaptorQ codes, a mode selective decoding algorithm for RaptorQ code is proposed in this paper. Combined with the advantages of optimized inactivation decoding Gaussian elimination(OIDGE) algorithm and dimensionality reduced fast decoding (DRFD) algorithm, the actual situation and the efficiency of the channel decoding algorithm are taken into account, and then the corresponding decoding mode is adopted according to current packet loss rate. Experiments are carried out on embedded system, and the results show that the decoder can select the appropriate algorithm adaptive to the packet loss rate. This improves the decoding efficiency of RaptorQ codes in a certain extent. application layer FEC; fountain code; RaptorQ code; Gaussian elimination decoding 李越,張立軍,李明齊,等.一種RaptorQ碼的模式選擇解碼算法 [J]. 電視技術,2016,40(12):120-124. LI Y, ZHANG L J, LI M Q,et al.A mode selection algorithm for RaptorQ code decoding[J]. Video engineering,2016,40(12):120-124. TN911.22 A 10.16280/j.videoe.2016.12.023 中科院戰略性先導專項子課題(XDA06010301);國家基金委青年科學基金項目(61401440);上海市國際科技合作基金項目(14510722300) 2016-04-272 模式選擇算法
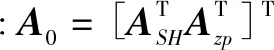
3 實驗結果
4 結論

