客戶數量變動擾動下的配送車輛調度研究

曹慶奎，趙麗飛，任向陽

(河北工程大學 管理工程與商學院，河北 邯鄲056038)

客戶數量變動擾動下的配送車輛調度研究

曹慶奎，趙麗飛，任向陽

(河北工程大學 管理工程與商學院，河北 邯鄲056038)

針對物流配送活動中經常出現有新客戶訂貨或者是已經訂貨的客戶退貨的情況。將客戶關系管理與物流配送干擾管理相結合，在考慮客戶等級劃分的條件下，以擾動過程中的客戶數量變動為研究對象，針對客戶數量變動問題，構建客戶數量變動擾動下的配送車輛干擾管理模型，運用模擬植物生長算法對模型進行優化求解。結合具體實例,驗證了模型及算法的有效性。

客戶數量；客戶等級劃分；干擾管理；車輛調度；模擬植物生長算法

物流配送活動中經常出現有新客戶訂貨或者是已經訂貨的客戶退貨的情況。國內外的研究學者對干擾管理進行了大量的研究，Rhalibi等[1-2]建立相關模型有效地解決了帶有時間限制的車輛延遲問題；王明春[3-4]等提出了一種帶有時間窗的擾動恢復策略；胡祥培[5-6]等提出了從客戶滿意度、配送成本以及路徑偏離量三方面來衡量，改進智能優化算法對模型求解；丁秋雷等提出了基于前景理論的物流配送干擾管理模型；Ding[4,8-11]建立了車輛調度的干擾模型；模擬植物生長算法是李彤提出來的一種智能優化算法，該算法目前已經被廣泛的運用到各領域。目前的研究中對于客戶數量變動方面的擾動的研究并不完善，多數是將其歸納為需求量變動，并沒有考慮客戶的重要程度。本文在考慮客戶等級劃分的前提下，建立了客戶數量變動擾動下的配送車輛干擾管理模型，并結合實例，利用模擬植物生長算法對模型進行求解。

1 基于云模型的客戶細分

針對物流企業客戶的特點，從客戶的當前價值、客戶潛在價值以及關系價值三方面對物流企業客戶的客戶價值進行分析，建立物流企業客戶價值評價指標體系，將云模型以及局部變權理論相結合對各項指標進行處理，對物流企業的客戶進行等級劃分。

1.1客戶價值評價指標體系

對于物流企業的客戶，根據物流企業的特點，從客戶的全生命周期出發構建物流企業客戶價值評價指標體系，該指標體系中有3個一級指標，11個二級指標，如圖1所示：

1.2客戶指標權重的確定

利用德爾菲法將11項二級指標重要性進行兩兩對比打分，在第一輪打分結束以后，利用云模型對指標的打分進行修正。最終確定各個指標之間的對比情況。客戶周期服務費用與客戶服務費用兩個指標間的打分過程如圖2所示。得到的判斷矩陣如表1所示：對表1中數據歸一化處理后，得到各個二級指標的初始權重，如表2所示：

1.3客戶分類綜合評價值計算

在得到上述表格中的權重以后，將物流公司客戶的各組數據利用公式(1)計算綜合評價值，其中各二級指標作為常權變量。

(1)

其中：Wi(0)表示各項指標初始權重；Xia表示變權變量；Xi表示常權變量；a表示補償系數，在0～1之間取值[16]。

表1 專家打分后得到的判斷矩陣

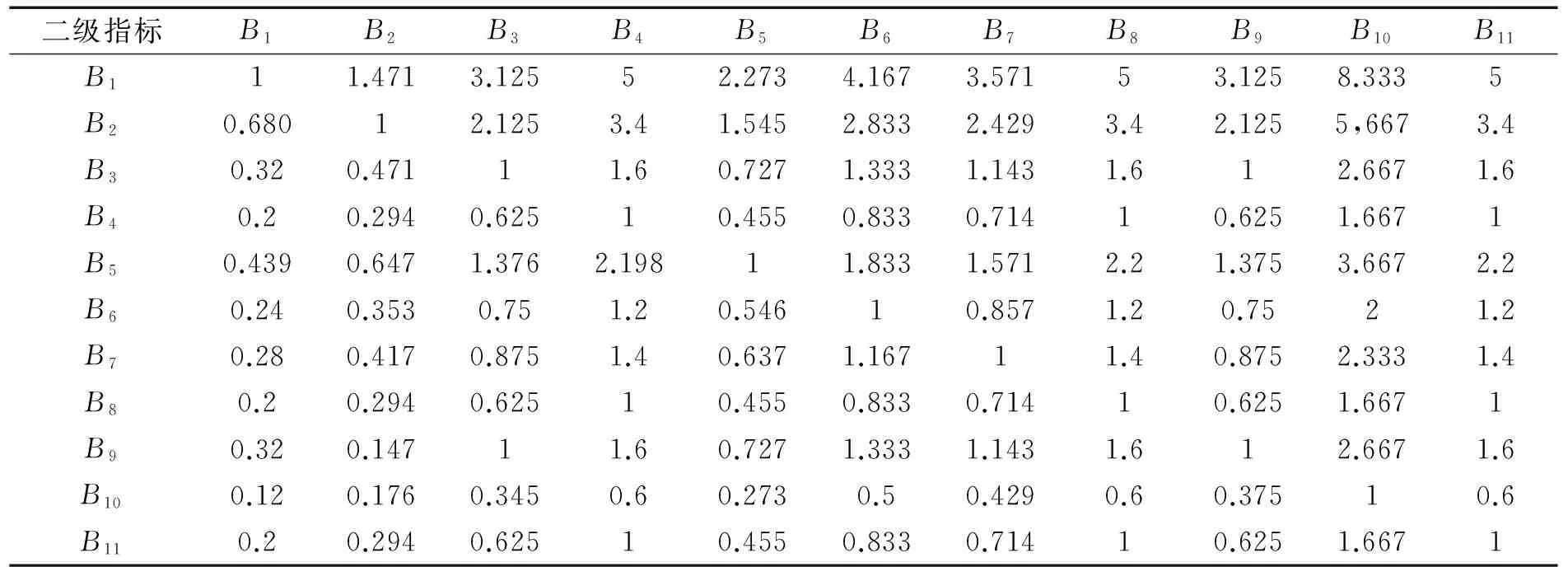
二級指標B1B2B3B4B5B6B7B8B9B10B11B111.4713.12552.2734.1673.57153.1258.3335B20.68012.1253.41.5452.8332.4293.42.1255,6673.4B30.320.47111.60.7271.3331.1431.612.6671.6B40.20.2940.62510.4550.8330.71410.6251.6671B50.4390.6471.3762.19811.8331.5712.21.3753.6672.2B60.240.3530.751.20.54610.8571.20.7521.2B70.280.4170.8751.40.6371.16711.40.8752.3331.4B80.20.2940.62510.4550.8330.71410.6251.6671B90.320.14711.60.7271.3331.1431.612.6671.6B100.120.1760.3450.60.2730.50.4290.60.37510.6B110.20.2940.62510.4550.8330.71410.6251.6671

表2 各二級指標的初始權重

1.4客戶等級劃分

定義客戶的評語集為：V=(v1,v2,v3)，其中v1(85～100分)，表示重要客戶；v2(40～85分)表示較重要客戶；v3(0～40分)表示一般客戶。依據公式(1)計算出的客戶綜合評價值物流企業客戶根據其不同的客戶價值進行客戶等級劃分。

2 考慮客戶細分配送干擾管理模型

首先，建立初始的物流配送數學模型，配送過程中擾動發生以后，在原始配送方案[7]的基礎上，根據客戶的重要程度不同，對初始配送方案進行調整，構建考慮客戶等級劃分的物流配送車輛調度模型。

2.1參數變量及說明

m：未完成配送任務客戶總數量；DS：未被服務的客戶；V：客戶點集合，V={v0,v1,v2,…,vm+K},v0代表初始配送中心；v1,…,vm代表未完成配送任務的客戶；vm+1,…,vm+K表示當前配送車輛所在位置，即虛擬配送中心；Dp:對貨物到達的不滿意程度；DF:物流配送運營商對配送成本的不滿意度；DN:配送業務員即貨車司機對路徑偏離量的不滿意程度；VC：表示虛擬客戶點集；RT=VC∪DS；tijk為路徑偏離參數，并且

2.2考慮客戶細分的擾動度量函數

客戶不滿意度度量：這里假定客戶的不滿意程度只與時間有關，由于在構建模型時，目標函數使用最小化構建，因此這里采用客戶的不滿意程度。客戶接受貨物的時間一般會同時滿足軟時間窗與硬時間窗，即當貨物送達的時間在客戶要求的時間內，客戶的滿意程度最高，當貨物配送時間早于或者遲于客戶要求的時間時，客戶的滿意度就會下降，但是并不會拒絕收貨。因此，這里設置相應的懲罰函數Pi(ti)[11]；

(2)

其中：M是無窮大的數，ai、bi、mi和ni均為懲罰系數。

(2)式是對某一客戶不滿意程度的度量，對于配送系統中整體不滿意度的度量，本文采用客戶分級的策略對整體的擾動大小進行度量，根據客戶分類，用Z1、Z2和Z3分別表示客戶所屬等級的集合，Z1表示重要客戶，Z2表示較重要客戶，Z3表示一般客戶。同時，分別定義這三類客戶重要程度相關系數為α、β和γ，因此，客戶整體不滿意度度量公式為：

(3)

物流服務提供商配送成本度量：這里所說的配送成本區別于原始的配送成本，指的是擾動發生以后所產生的成本偏差，當擾動事件發生以后主要應對方法有兩種，等待和救援。由于物流配送中心一般沒有閑置的車輛，并且啟用救援車輛的成本一般會比較大，因此，一般情況下不予采用。對于等待有兩種情況，分別為重新調度和不重新調度。若不重新調度，那么由干擾事件產生的額外的配送成本為零；如果重新調度，配送路線的長度會大于原計劃，此時，物流提供商配送成本擾動度量公式為:

(4)

貨車司機滿意度度量：貨車司機的滿意程度主要由路徑偏離量引起，因此用路徑偏離量來代替貨車司機的滿意度。路徑偏離量擾動公式為：

(5)

2.3字典序的多目標干擾管理模型

以考慮客戶細分的擾動度量函數為基礎，采用字典序的多目標規劃方法，構建基于客戶等級劃分的車輛調度干擾模型。

minLex=(P1:DP,P2:DF,P3:DN)

(6)

P1≥P2≥P3

(7)

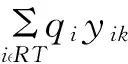
(8)

(9)

(10)

(11)

ti≥ETii=1,2,3,…,m

(12)

ti+wi≤LTii=1,2,3,…,m

(13)

(6)式為目標函數表達式，表示擾動發生以后對整個系統的擾動最小；(7)式表示不同目標的優先級，由于采用字典序建立多目標模型，該模型中客戶不滿意度為一級目標，對配送成本的擾動作為二級優化目標，貨車司機不滿意度為三級優化目標；(8)式表示車的貨運量不能大于其額定的承載量；(9)式表示每輛車都從虛擬配送中心出發；(10)式表示車輛對客戶服務結束以后，返回初始配送中心；(11)表示各變量之間的關系；(12)、(13)式表示滿足客戶時間窗。

3 模擬植物生長優化算法設計

利用模擬植物生長算法對該模型求解，根據上述建立的車輛調度干擾管理模型可知，該優化模型為字典序多目標優化模型，在求解上述模型時，逐級優化。具體步驟如下：

步驟一：確定擾動發生后的初始可行方案即樹根，記為x0，編碼方式采用自然數編碼，隨機產生碼串以后，對該碼串是否滿足約束條件進行檢驗，如果滿足約束條件，求出初始調度方案對應的函數值，記為f(x0)，并將其作為當前的最優解。

步驟二：以初始調度方案為基點，在其鄰域內進行2N次搜索并產生新的生長點，對新的生長點進行約束條件的校驗，當滿足約束條件時，求出各生長點相應的函數值，并與f(x0)進行對比，如果新生長點的函數值小于f(x0)，則用新的生長點替換f(x0)，記為f(x1)。當新的生長點的函數值大于f(x0)或者不符合約束條件的則直接舍棄。

步驟三：根據形態素公式計算待生長點集內所有生長點的形態素濃度P1,P2,…,Pn。

步驟四：建立[0,1]之間的概率空間，利用計算機隨機選取下一次的生長點。

步驟五：重復步驟二到步驟五，當沒有新的生長點產生或者達到迭代次數的時候終止。

4 案例分析

以某物流公司配送任務對模型進行求解計算，配送中心坐標為[21,21]，有4輛車進行配送，本次送貨需要對13個客戶點進行配送，假設每輛車的載重量為10 t，勻速行駛且行駛速度為40 km/h，每個配送車輛的固定成本為150 元/輛，變動成本為每行駛一公里增加2.5元。當t=1.5 h，客戶12取消本次訂貨。

首先，利用上述云模型對客戶等級劃分，各個客戶的情況如表3所示，其中分別表示客戶所屬集合，Z1其中表示重要客戶，Z2表示較為重要客戶，Z3表示一般客戶。

表3 客戶情況一覽表

然后利用模擬植物生長算法對客戶數量變動后的干擾管理模型以及全局的重新調度模型進行求解。本文采用matlab7.1編程實現模擬植物生長算法對該模型的求解。求解對比結果見表4。

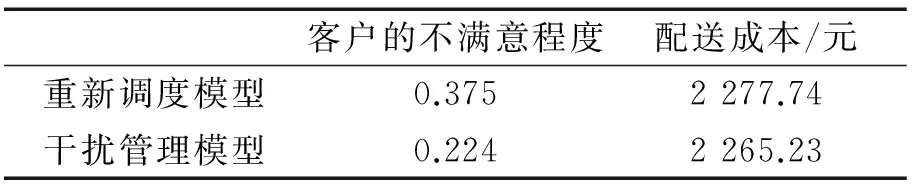
表4 物流運營商滿意度對比

經對比結果分析可知，數量變動后干擾管理模型與重新調度模型的對比中，雖然成本比較接近，但是，客戶的不滿意程度比一般的干擾配送管理的滿意程度低15%。

5 結論

本文考慮客戶價值，構建了客戶數量變動下的車輛調度干擾管理模型，利用云模型以及變權理論對客戶的重要程度進行動態劃分，將物流企業有限的資源合理分配在客戶中。對結果分析可知，數量變動后干擾管理模型與重新調度模型對比，雖然配送成本比較接近，但是，客戶的不滿意程度降低了15%。

[1]RHALIBI A E，KELLEHER G.An approach to dynamic vehicle routing, rescheduling and disruption metrics[C]//IEEE International conference on systems, Man and Cybernetics，2003(4)：3613-3618.

[2]HUSIMAN D，FRELING R，WAGEIMANS A P M.A robust solution approach to the dynamic vehicle scheduling problem[J].Transportation Science，2004，38(4)：447-458.

[3]王明春，高成修，曾永廷.VRPTW的擾動回復及其TABU-SEARCH算法[J].數學雜志，2006，26(32)：231-236.

[4]王旭坪，阮俊虎，張 凱，等.有模糊時間窗的車輛調度組合干擾管理研究[J].管理科學學報，2011，14(6)：2-15.

[5]胡祥培，孫麗君，王亞楠.物流配送系統干擾管理模型研究[J].管理科學學報，2011，14(1)：50-60.

[6]閆卓楠，王承文，俞 虹.城市災害應急物流配送干擾管理系統模型研究[J].工程管理學報，2014，28(2)：61-65.

[7]丁秋雷，胡祥培，姜 洋.基于前景理論的物流配送干擾管理模型研究[J].管理科學學報，2014，17(11)：1-19.

[8]DING Q，HU X，WANG Y.A model of disruption management for solving delivery delay[C]//Advances in Intelligence Decision Technologies: Proceedings of the Second KES International Symposium IDT, Baltimore, USA, 2010：227-237.

[9]胡祥培，于 楠，丁秋雷.物流配送車輛的干擾管理序貫決策方法研究[J].數學雜志，2006，26(32)：231-236.

[10]丁秋雷. 物流配送受擾延遲問題的干擾管理模型研究[J].中國管理信息化，2012，15(22)：59-61.

[11]丁秋雷，胡祥培，姜 洋.物流配送受擾問題的干擾管理兩階段決策方法[J].運籌與管理，2012，21(6)：84-93.

[12]曹慶奎，劉新雨，任向陽.基于模擬植物生長算法的車輛調度問題[J].系統工程理論與實踐，2015，35(6)：1449-1456.

[13]唐海波，葉春明，張新功.應用模擬植物生長算法求解置換流水車間調度問題[J].計算機應用研究，2010，27(10)：3670-3672.

[14]郗 瑩，馬 良，戴秋萍.多目標旅行商問題的模擬植物生長算法求解[J].計算機應用研究，2012，29(10)：3733-3735.

[15]龔承晉，李明明.基于云模型及變權理論的中小零擔物流企業客戶分類方法研究[J].物流科技，2014，37(4)：73-76.

(責任編輯 王利君)

Research on vehicle scheduling problem with customer quantity variation

CAOQingkui,ZHAOLifei,RENXiangyang

(SchoolofManagementEngineeringandBusiness,HebeiUniversityofEngineering,HebeiHandan056038,China)

Logisticsdistributionactivitiesoftenencounterwithnewcustomerorcustomerwhowantstoreturngoodsforrefund.Thecustomerrelationshipmanagementandthedisruptionmanagementwerecombinedtosetupthedistributionvehicledisruptionmanagementmodelunderthecustomersegmentationbytakingthecustomerquantitychangeastheobject.Finally,themodelwasoptimizedbytheplantgrowthsimulationalgorithm.Engineeringpracticeverifiedthevalidityofthemodelandalgorithm.

customerquantity;customergradeclassification;distributionmanagement;vehiclescheduling;plantgrowthsimulationalgorithm

1673-9469(2016)04-0108-05doi:10.3969/j.issn.1673-9469.2016.04.023

2016-07-07 特約專稿

國家自然科學基金資助項目(61375003)；河北省自然科學基金資助項目(F2014402040)；河北省社會科學基金資助項目(HB16GL026);河北省人才工程培養經費資助科研項目(A2016001120); 河北省教育廳科學研究計劃項目(SD161009)

曹慶奎(1963-)，男，河北唐山人，博士，教授，研究方向為物流與供應鏈管理。

F

A