子系統碼的一個圖的構造方法*

陳丙亞，白姍姍

(安徽理工大學 理學院,安徽 淮南 232007)

子系統碼的一個圖的構造方法*

陳丙亞，白姍姍

(安徽理工大學 理學院,安徽 淮南 232007)

子系統碼是具有消相干自由子空間、無噪子系統和量子糾錯碼混合特點的一類量子糾錯碼。介紹線性碼和子系統碼的基本知識，基于前人的研究，首次利用三元圖鄰接矩陣生成的三元線性碼構造子系統碼，并給出具體的子系統碼參數，進一步豐富已有結論，同時結合具體的例子，分析構造的子系統碼的性能，發現構造的子系統碼可以糾正小于或等于3個量子錯誤，且它們的碼率隨著碼長增大而增大。

子系統碼；三元圖；線性碼；鄰接矩陣

0 引 言

當前，子系統碼（也稱算子量子糾錯碼）已經成為量子編碼理論領域的一項重大發現。有關消相干自由子空間、無噪子系統和量子糾錯碼的最新研究表明，這三個方面的內容可以統一為子系統碼。子系統碼擁有一些特殊功能，如簡化綜合計算、易實現容錯操作等[1]。

Knill[2]和Kribs[3]等人首次提出子系統碼概念，即結合基本范式的量子糾錯碼的一般模式，也稱為算子量子糾錯碼。Kribs[3]和Bacon[4]等人對子系統碼的形式結構和它們與子系統碼的關系作了介紹和分析。2008年，Klappenecker[5]等人根據Clifford碼介紹了子系統碼的一種原始構造。Aly[6]等人則證明了在二進制和非二進制域上構造子系統碼的幾種方法。Qian[7]等人給出一類新的循環碼構造，并提供一類新的最優子系統碼。

本文首先介紹線性碼和子系統碼的基本知識，再利用三元圖的鄰接矩陣生成的線性碼構造新的子系統碼，最后給出具體的例子來分析文中構造的子系統碼的性能。

1 基本知識點

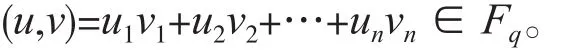
1.2 子系統碼

這部分將對子系統碼的背景做簡單介紹[5]。

令{|x x∈Fq}是復矢量空間Γq中關于標準Hermitian內積的一個固定的正交基，稱為計算基失。對a,b∈Fq，分別用X(a)|x=|x+a和Z(b)|x =ωtr(bx)|x定義Γq上的單位算子X(a)和Z(b)。

定義1[8]：一個((n,K,R,d))子系統碼是的子空間Q被分解成兩個向量空間的張量積，即Q=A?B，其中向量空間A的維數為K，向量空間B的維數為R。因此，Q中所有重量小于或等于d的錯誤都可以被A檢測。

我們稱A為子系統，B為協同子系統，而信息只在子系統A中被編碼。

((n,K,R,d))q或 [[n,k,r,d]]q， 其 中 k=logqK，r=logqR）子系統碼可以由Fq上的經典碼構造。下面給出Euclidean構造。

定理1[9]：若C是有限域Fq上長度為n的一個k'維線性碼，碼C的一個k''維子碼D=C∩C⊥且k'+k''＜n，則存在參數為[[n,n-(k'+k''),k'-k'',wt(D⊥C)]]q的子系統碼。

引理1[10]：設d是量子糾錯碼C的最小距離，則C可以糾正≤l個量子錯誤。

2 新的子系統碼構造

圖的鄰接矩陣是表示兩個事物之間具有的特定關系。用鄰接矩陣表示圖很容易確定圖中任意兩個頂點是否有邊相鄰。通常，圖是以其鄰接矩陣的形式貯存于計算機。

下面給出圖的鄰接矩陣的定義。

定義2[11-12]：對任意圖G，設v1,v2,…,vn和e1,e2,…,em（其中m和n分別表示點和邊數）分別表示G的頂點和邊，則伴隨與G的一個n×n矩陣A(G)=[aij]是鄰接矩陣。其中，aij是連接vi和vj的邊的數目。

文獻[13]中，Key、Moori和Rodignes給出由三元圖的鄰接矩陣生成三元線性碼的方法，同時也給出了由三元圖的鄰接矩陣生成的三元線性碼的參數，分別如引理2和引理3、引理4所述。

引理2[13]：設Ω是一個大小為n≥7的集合，令P=Ω(3)是大小為3的子集合，且對i=0,1,2，P=Ω(3)是3個圖Ai(n)的頂點集。設Ci(n)是域F3上圖Ai(n)的一個鄰接矩陣生成的線性碼。

引理3[13]：當n≥7且n≡1(mod3)時，存在三元線性碼其中2(n-3)＜n≤4(n-4)；當n≥10時，其對偶碼為且有

引理4[13]：當n≥10且n≡1(mod3)時，存在三元線性碼其對偶碼為

文獻[14]中，錢建發等人利用立方圖線圖生成的二元線性來構造量子糾錯碼和非對稱量子糾錯碼，得到了一類新的量子糾錯碼和非對稱量子糾錯碼。鑒于此，下面將利用三元圖的鄰接矩陣生成的三元線性碼來具體構造一批子系統碼，如引理5、定理2相關論述。

引理5[13]：當n≥7且n≡1(mod3)時,有C1(n)=

定理2：當n≥10且n≡1(mod3)時，存在參

證明：三元圖上的線性碼C1(n)和C2(n)滿 足 關 系可 驗 證 當時， 滿 足再根據定理1可知，可以構造參數為的子系統碼。

例如，當n分別取10,13,16,19,22和25時，其對應的線性碼和子系統碼，如表1所示。

從表1可以看出，所構造的子系統碼是新的。根據引理1可知，這些子系統碼可以糾正小于或等于3個量子錯誤，且它們的碼率分別為

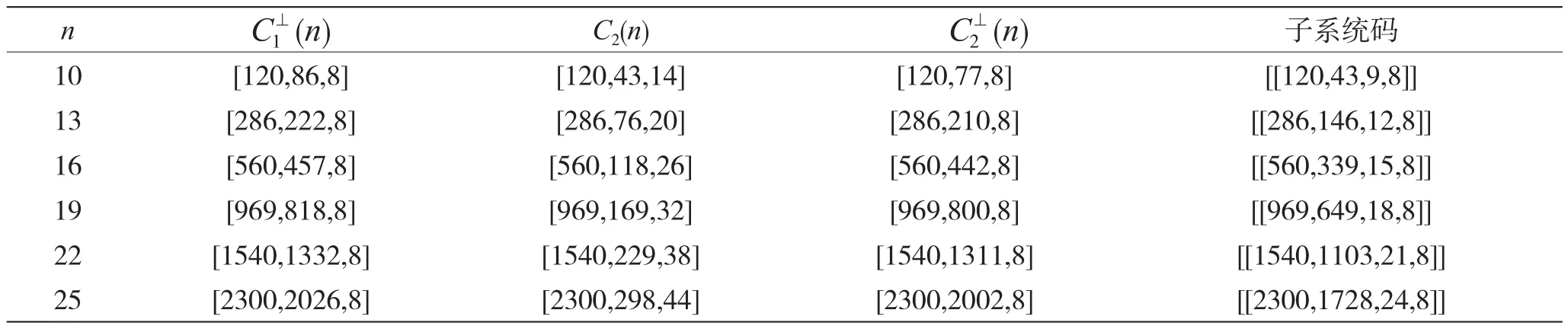
表1 帶具體參數的線性碼及其對應的子系統碼

3 結 語

本文首次利用三元圖的鄰接矩陣生成的三元線性碼構造子系統碼，得到了有具體參數的子系統碼。分析它們的性能發現，這些新的子系統碼可以糾正小于或等于3個量子錯誤，且它們的碼率隨著碼長n的增大而增大。

子系統碼是相對較新和富有成果的量子糾錯碼。對編碼者來說，如何利用更簡單、更快捷的方法構造出有具體參數和性能良好的子系統碼是子系統碼未來研究的熱點，這也將是本文的下一步工作。

[1] Aly S A.On Quantum and Classical Error Control Co-des:Constructions and Applications[D].State of Texas:Texas A＆M University,2008.

[2] Knill E.Group representations,error bases and quantum[R].New Mexico:Los Alamos National Laboratory,1996.

[3] Kribs D W,Laflamme R,Poulin D.Unified and Generalied Approach to Quantum Error Correction[J].Physical Review Letters,2005,94(18):1-4.

[4] Bacon D.Operator Quantum Error Correcting Subsystems for Self-Correcting Quantum Memories[J]. PhysicalReview A,2005,73(01):1-13.

[5] Klappenecker A,Sarvpalli P K.Clifford Code Constructions of Operator Quantum Error-Correcting Codes[J].Information Theory IEEE Transactions on,2008,54(12):5760-5765.

[6] Aly S A,Klappeneckr A.Constructions of Subsystem Codes over Finite Fields[J].International Journal of Quan-tum Information,2011,7(05):891-912.

[7] Qian J F,Zhang L N.Constructions of Optimal Subsystem Codes[J].Modern Physics Letters B,2012,26(26):1-8.

[8] Aly S A,Klappenecker A.Subsysem Code Constructions[C]. Toronto,Canada:In Proc.2008 IEEE International Symposium on Information Theory,2008:369-373.

[9] Aly S A,Klappenecker A,Sarvepalli PK.Subsystem Cod-es[C].In 44th Annual Conference on Commuication,Control,and Computing,2006.

[10] 馮克勤.量子糾錯碼[M].北京:科學出版社,2010:55-80. FENG Ke-qin.The Algebraic Theory of Quantum Error Correction Code[M].Beijing:Tsinghua University Press,2010:55-80.

[11] Bondy J A,Murty U S R.圖論及其應用[M].北京:科學出版社,1984:1-17. Bondy J A,Murty U S R.Graph Theory with Applications[M].Beijing:Tsinghua University Press,1984:1-17.

[12] 馮賓.新的量子糾錯碼的構造[J].信息安全與通信保密,2014(05):118. FENG Bin.Construction of New Quantum Error Correction Codes[J].Information Security and Communication Security,2014(05):118.

[13] Key J D,Morri J,Rodigues B G..Ternary Codes from Graph on Triples[J].Discrete Mathematics,2009(309):4663-4681.

[14] 錢建發,張莉娜.利用立方圖的線圖構造量子糾錯碼[J].計算機工程與應用,2013,49(06):16-18. QIAN Jian-fa,ZHANG Li-Na.Construction of Quantum Error-Correcting Codes With Linear Graph on Cubic Graph[J].Computer Engineering and Application,2013,49(06):16-18.

陳丙亞（1990—），女，碩士，主要研究方向為糾錯碼理論及應用；

白姍姍（1989—），女，碩士，主要研究方向為糾錯碼理論及應用。

Construction of Subsystem Codes From Graphs

CHEN Bing-ya, BAI Shan-shan
(College of Science, Anhui University of Science and Technology, Huainan Anhui 232007 China)

Subsystem codes are a class of quantum error-correcting codes that combine the features of decoherence free subspaces,noiseless subsystems and quantum error-correcting codes.This paper introduces the basic knowledge of linear codes and subsystem codes, based on the previous studies,ternary codes on ternary graph are used for the first time to construct the subsystem codes.Some specific subsystem codes with specific parameters are given in this paper,which futher enrich the existing conclusions.In the final, analyze their performance,namely the constructed subsystem codes can correct less than or equal to 3 quantum errors,and their rate increases with the increase of their length.

Subsystem codes; Ternary graphs; Linear codes;Adjacency matrix

TN911.2

：A

：1002-0802(2016)-06-0679-04

10.3969/j.issn.1002-0802.2016.06.006

2016-02-02；

：2016-05-02 Received date:2016-02-02; Revised date:2016-05-02

安徽省自然科學基金（No.1408085MA05）

Foundation Item:Natural Science Foundation of Anhui Province(No.1408085MA05)