一種改進的變步長LMS算法在Costas環中的應用*

馬叢珊，高 俊，婁景藝

(海軍工程大學 電子工程學院，湖北 武漢 430033)

一種改進的變步長LMS算法在Costas環中的應用*

馬叢珊，高 俊，婁景藝

(海軍工程大學 電子工程學院，湖北 武漢 430033)

針對傳統固定步長LMS算法在穩態誤差、收斂速度、跟蹤速度方面無法兼得的問題，比較多種不同的變步長LMS算法,提出了一種改進變步長LMS算法。通過對該算法進行仿真分析，發現該算法不僅滿足穩態誤差、收斂速度、跟蹤速度各方面的要求，還減小了噪聲對算法的干擾。同時，為了解決科斯塔斯（Costas）環在現實硬件實現中兩路信號無法完全一致的問題，將改進變步長LMS算法運用到科斯塔斯（Costas）環中，成功實現了載波恢復。

LMS算法;變步長;科斯塔斯（Costas）環;載波恢復

0 引 言

在短波通信系統接收機中，如何產生與載波信號同頻同相的本地載波信號，是最后輸出優質解調信號的重要條件之一。而隨著通信、導航等行業的發展，對短波接收機的要求也越來越高。而在傳統的載波同步方法中，無論是平方環還是科斯塔斯（Costas）環，都需要I、Q兩路信號，且要求經過低通濾波器后的兩路信號具有頻率相同、相位相差90°的特性。然而，現實的硬件設計很難滿足。

而在LMS算法中，由于傳統固定步長LMS算法[1]無法在穩態誤差、收斂速度和跟蹤速度方面獲得最優性能，因此本文在對多種變步長LMS算法進行討論的基礎上，提出一種改進的變步長LMS算法。仿真分析表明，該算法不僅可滿足穩態誤差、收斂速度和跟蹤速度的要求，而且對噪聲有很好的抑制作用。

同時，本文嘗試將改進變步長LMS算法運用到科斯塔斯（Costas）環中，只需一路信號，即可完成最后的本地載波提取。

1 算法推導

1.1 固定步長LMS算法

最小均方（Least Mean Square，LMS）算法是線性自適應濾波算法[2]。它包含了濾波和自適應兩個基本過程，設計準則是最小均方誤差準則（MinimumMean Square Error，MMSE），即濾波器的期望輸出與實際輸出響應的均方誤差最小。設e(n)為濾波器在n時刻的誤差，濾波器的輸入為x(n)，濾波器的輸出為y(n)，濾波器的抽頭權向量為，步長參數為μ。

LMS算法流程如圖1所示。

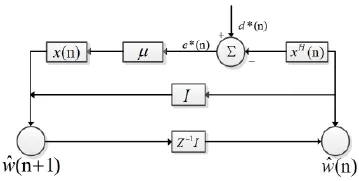
圖1 LMS算法流程

（1）輸入μ和x(n), x(n)=[x(n),x(n-1),…,x(n-M+1)]T，M為濾波器長度；

（4）計算出濾波器在n時刻的誤差e(n)=d(n)-y(n)；

（5）計算新的抽頭權向量估計值

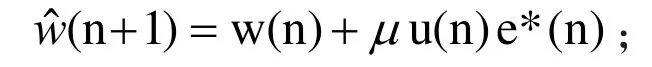
1.2 變步長LMS算法

為了使LMS算法具有好的穩態誤差，同時收斂速度快、跟蹤速度快，需要采用改變步長參數的方法[4]。以下就常見的四種變步長LMS算法進行討論。

（1）基于抽樣函數的變步長LMS算法

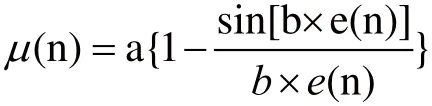
（2）基于雙曲正切函數的變步長LMS算法

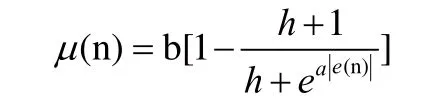
（3）基于Lorentzian函數的變步長LMS算 法

在Lorentzian函數y=log[1+e(n)2]的基礎上，文獻[7]提出了一種新的算法，希望能提高收斂速度和跟蹤速度。

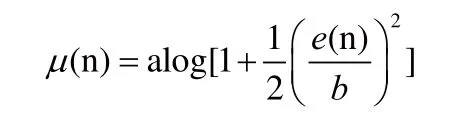
（4）基于Sigmoid函數的變步長LMS算法

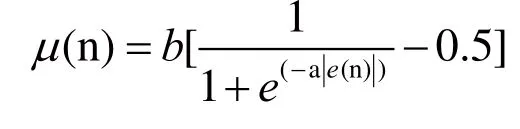
1.3 算法的選擇和改進

四種算法的μ(n)和e(n)的關系如圖2所示。基于抽樣函數的算法在e(n)趨近0時，步長參數μ(n)變化緩慢，但是當e(n)較大時，有很明顯的旁瓣。基于雙曲正切函數、基于Lorentzian函數和基于Sigmoid函數的算法，在e(n)較大時，μ(n)擁有較快的變化速度，但是在接近穩態時，μ(n)的變化速度沒有明顯減小，容易造成穩態失調。四種算法里，只有基于抽樣函數的算法，在e(n)為0的時候μ(n)可以為0，其余三種算法均存在誤差。計算量上，基于Lorentzian函數的算法存在平方項和log項，使得計算量大大增加。同時，四種算法的抗干擾性均不佳。

為了進一步檢驗四種算法的穩態誤差、 收斂速度和跟蹤速度，將對這四種算法進行仿真比較。

圖2 四種算法的(n)和e(n)的關系對比

搭建仿真平臺條件：

（1）濾波器的階數為2。

（2）迭代次數為2 000。

（3）仿真的統計次數為200。

（4）未知系統的FTR系數為w=[0.6,0.3]，在第1 000個抽樣點時系統發生突變，突變后的FTR系數為w=[0.5,0.1]。

（5）系統的輸入為零均值、方差為1的高斯白噪聲。

（6）系統的加性噪聲為零均值、方差為0.04的高斯白噪聲。

仿真結果如圖3所示。

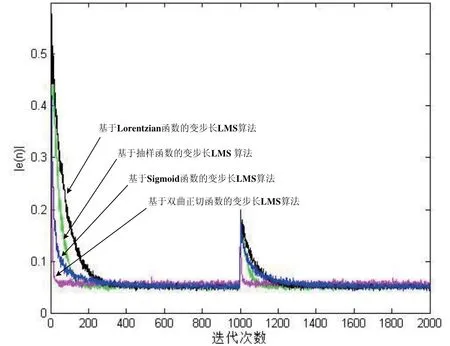
圖3 四種變步長算法的比較

如圖3所示，在系統穩態誤差相差無幾的情況下，基于雙曲正切函數的變步長LMS算法具有很快的收斂速度和追蹤速度。但是，如前文所述，這種算法的抗噪聲能力較差。當未知系統存在干擾噪聲且噪聲的自相關性很強時，算法的性能將受到很大影響。

因此，本文將e(n)改為e(n)e(n-1)，從而較好地控制噪聲對算法的影響。這是因為誤差信號中的噪聲自相關性一般很強，而互相關性一般很差，用e(n)e(n-1)可以通過噪聲較差的互相關性將其除去，從而降低噪聲對步長參數μ(n)的影響[9]。所以，改進后基于雙曲正切函數的變步長LMS的相關參數如下：

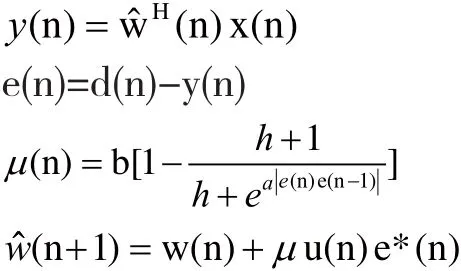
修改后基于雙曲正切函數的變步長LMS算法與原始基于雙曲正切函數的變步長LMS算法的仿真比較，如圖4所示。修改后基于雙曲正切函數的變步長LMS算法在誤差信號較大時，擁有較快的收斂速度，而在誤差信號接近零時，又擁有較慢的收斂速度，減小了系統的穩態失調。同時，由圖5、圖6、圖7可知，通過改變a、b、h的值，可以改變μ(n)和e(n)的關系。其中，a越大、b越大、h越小時，算法的收斂速度越快。相較b的值，a和h的值更能影響曲線的底部特性。這將影響到e(n)趨近于0時的系統穩定性。此外，算法對a值的變化更加敏感。最終，隨著e(n)的增大，步長μ(n)將變為一樣。而b值更能影響曲線的初始值。這將影響到系統的最初收斂步長。

此外，通過計算，在輸入相同信號和相同噪聲的情況下，修改后的算法將原基于雙曲正切函數的算法的信噪比提高了10 dB，一定程度上也減小了噪聲對算法的影響。

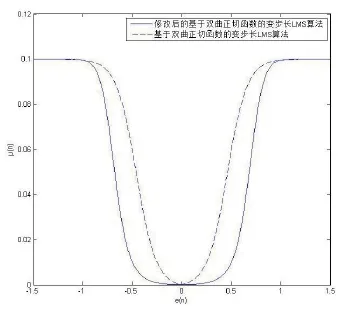
圖4 兩種基于雙曲正切函數的變步長LMS算法的比較

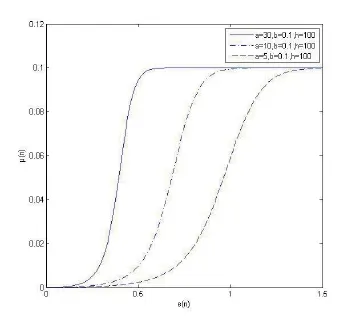
圖5 a值變化時μ(n)和e(n)的關系

圖6 b值變化時μ(n)和e(n)的關系

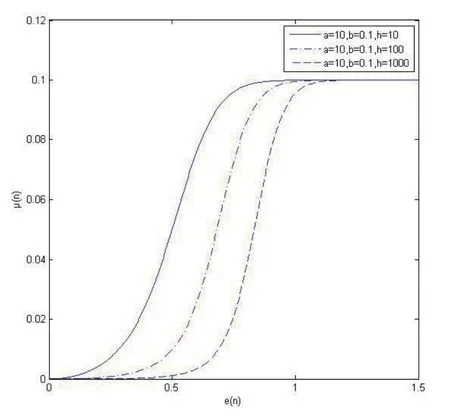
圖7 h值變化時μ(n)和e(n)的關系

2 科斯塔斯（Costas）環原理

在接收機中，為了獲得一個與接收信號載波同頻同相的本地震蕩信號，需要進行載波同步[10]。載波同步的方法很多，如平方環、科斯塔斯（Costas）環、再調制等。本文采用科斯塔斯（Costas）環進行載波同步。科斯塔斯（Costas）環的載波同步原理 如圖8所示。

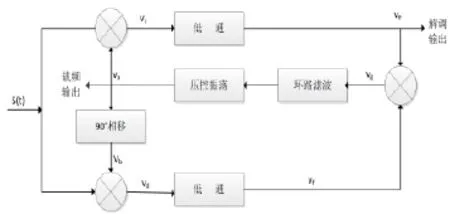
圖8 科斯塔斯（Cos tas）環的原理

接收信號s(t)被送入I、Q兩路，分別與va和vb相乘，其中

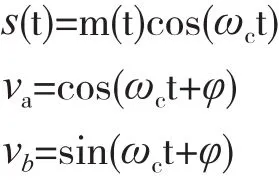
分別經過相乘器后，可得

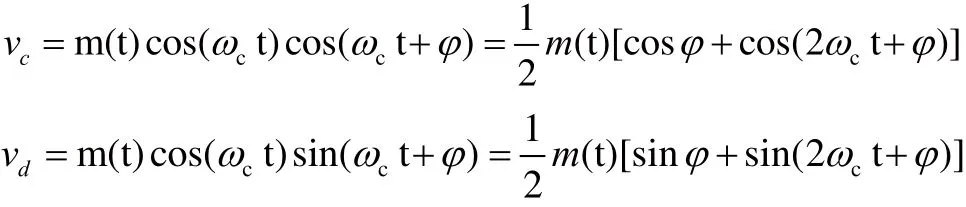
經過低通濾波器后，分別可得

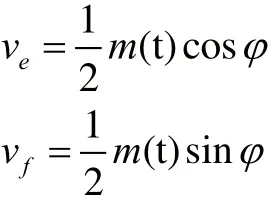
將ve與vf同時經過相乘器，有

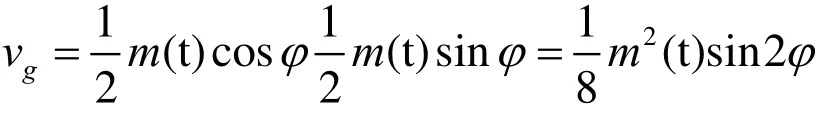
當m(t)為BPSK調制時，m2(t)=1，且當φ很小時，可得

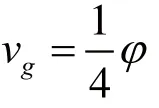
將vg輸入到壓控振蕩器中，調節壓控振蕩器的輸出va。當φ=0時，vg=0，此時的va即為科斯塔斯（Costas）環的輸出載波，用它來做相干解調的本地載波時，得到的ve即為解調輸出。

3 變步長LMS算法在科斯塔斯（Costas）環中的應用

將改進的基于正切曲線的LMS算法應用于科斯塔斯（Costas）環中，用算法的迭代結果取代原來I、Q兩路經過相乘器后的結果，如圖9所示。

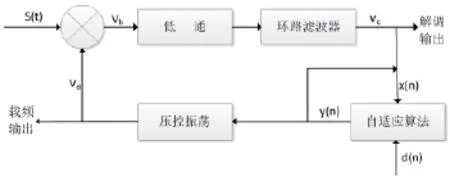
圖9 運用變步長LMS算法的科斯塔斯（Costas）環

接收信號s(t)被送入I路與va相乘，其中

經過相乘器后，可得

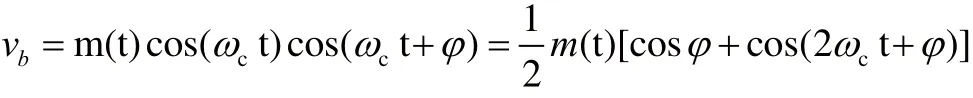
分別經過低通濾波器和環路濾波器后，可得

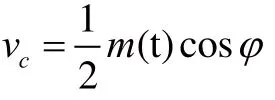
當m(t)為BPSK調制時，m2(t)=1，可得

將vc作為LMS算法的輸入x(n)，而算法的期望輸出d(n)=0。通過不斷迭代調整，當e(n)→0時，將此時所得的y(n)輸入給壓控振蕩器所得的va，即為運用LMS算法的科斯塔斯環（Costas）環的輸出載波，用它來做相干解調的本地載波時，得到的vc即為解調輸出。如圖10所示，假設信噪比為-20 dB，通過MATLAB仿真，最后φ值趨近于零，此時va=cos(ωct)即為提取的本地載波，符合對科斯塔斯（Costas）環設計的最基本要求。

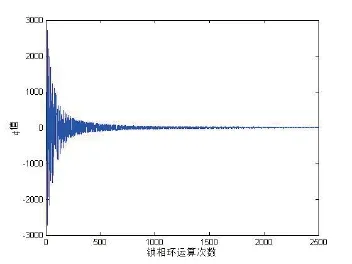
圖10 φ值的變化情況

4 結 語

通過比較前人的算法，提出了一種改進的變步長LMS算法，并將其成功應用于斯塔斯（Costas）環，實現了本地載波的提取。通過仿真分析提出的改進算法變步長LMS算法，發現其不僅滿足穩態誤差、收斂速度、跟蹤速度各方面的要求，還減小了噪聲對算法的干擾。同時，通過MATLAB仿真可以看出，這種基于變步長LMS算法的科斯塔斯（Costas）環，可以很好地完成本地載波的提取，很好地解決了科斯塔斯（Costas）環在現實硬件實現中兩路信號無法完全一致的問題。

[1] 周志文.變步長LMS算法預失真仿真與實現[J].通信技術,2013,46(09):111-114. ZHOU Zhi-wen.Simulation and Implementation of Polynomial Predistortion Based on Variable-step LMS Algorithm[J]. Communications Technology,2013,46(09):111-114.

[2] Simon Haykin.自適應濾波器原理[M].北京:電子工業出版社,2006. Simon Haykin. Adaptive Filter Theory[M]. Beijing:Publishing House of Electronic Industry,2006.

[3] Kwong R H,Johnston E W.A Variable Step Size LMS Algorithm [J].IEEE Trans on Signal Processing,1992,40(07):1663-1664.

[4] 蘭瑞明,唐普英.一種新的變步長LMS自適應算法[J].系統工程與電子技術,2005,27(07)：3172-3175. LAN Rui-ming,TANG Pu-ying.New Variable-step LMS Adaptive Algorithm[J].Systems Engineering and Electron ics,2006,27(07):109-112.

[5] 詹國強,吳正國.一種新的變步長LMS自適應濾波算法[J].海軍工程大學學報,2006,18(02):109-112. ZHAN Guo-qiang, WU Zheng-guo. A Novel Variable Step Size Adaptive Filtering LMS Algorithm Based on Sample Function[J].Journal Of Naval University Of Engi neering,2006,18(02):109-112.

[6] 張中華,張瑞金.一種新的變步長LMS自適應濾波算法及性能分析[J].系統工程與電子技術,2009,31(09):2238-2241. ZHANG Zhong-hua,ZHANG Rui-jin.New Variable Step Size LMS Adaptive Filtering Algorithm and Its Performance Analysis[J].Systems Engineering and Electr onics,2009,31(09):2238-2241.

[7] 劉劍鋒,蔣卓勤,李娟.一種基于Lorentzian函數的變步長LMS自適應濾波算法[J].指揮控制與仿真,2009,31(02):42-44. LIU Jian-feng,JIANG Zhuo-qin, LI Juan. A Novel Variable Step-Size LMS Adaptive Filtering AlgorithmBased on Lorentzian Function [J].Command Control &Simulation,2009,31(02):42-44.

[8] 覃景繁,歐陽景正.一種新的變步長自適應濾波算法[J].數據采集與處理,1997,12(03):171-194. TAN Jing-fan, OU YANG Jing-zheng.New Variable-step LMS Adaptive Algorithm [J].Journal of Data Acquisition & Processing,1997,12(03):171-194.

[9] 沈大偉,賀思.一種改進的變步長變更新速率LMS自適應算法[J].電子測量技術,2007,30(06):52-54. SHEN Da-wei,HE Si.A Modified Variable Step Size and Multi-rate Updated LMS Adaptive Filtering Algorithm and Its Simulation[J].Electronic Measurement Technology,2007,30(06):171-194.

[10] 田嘉,王偉,史平彥.數字Costas環的matlab仿真及其FPGA實現[J].微電子學與計算機,2011,28(11):69-71. TIAN Jia, WANG Wei, SHI Yan-ping. Simulation of Matlab and Implementation of FPGA Platform on Digital Costas Loop[J].Microelectronics & Computer,2011,28(11):69-71.

馬叢珊（1990—），女，碩士研究生，主要研究方向為數字理論與技術；

高 俊（1957—），男，博士，博士生導師，教授，主要研究方向為通信理論與技術、無線通信；

婁景藝（1979—），女，博士，副教授，研究方向為數字通信、衛星通信。

Application of A Modified Variable-step LMS Algorithm in the Costas Loop

MA Cong-shan,GAO Jun,LOU Jing-yi
(College of Electronic Engineering, Naval University of Engineering, Wuhan Hubei 430033,China)

Aiming at traditional constant-step LMS algorithm cannot simultaneously satisfy the steadystate error, the convergence speed and tracking speed, comparing different Variable-step LMS algorithm, a Modified Variable-step LMS algorithm is proposed. Simulation and analysis on the algorithm indicate that the algorithm not only can simultaneously satisfy the steady-state error, the convergence speed and tracking speed, but also can decrease the interference of noise. At the same time, it is difficult for Costas to have Identical two-way signal in the hardware implementation. A Modified Variable-step LMS algorithm is applied Costas. It is batter at carrier recovery.

LMS algorithm; Variable-step; Costas loop; carrier recovery

TN911

：A

：1002-0802(2016)-06-0673-06

10.3969/j.issn.1002-0802.2016.06.005

2016-02-15;

：2016-05-07 Received date:2016-02-15;Revised date:2016-05-07